производные от скаляров, векторов, и тензоры второго порядка по отношению к тензорам второго порядка широко используются в механике сплошной среды. Эти производные используются в теориях нелинейной упругости и пластичности, в частности, при разработке алгоритмов для численного моделирования.
производная по направлению обеспечивает систематический способ нахождения этих производных.
Содержание
- 1 Производные по векторам и тензоры второго порядка
- 1.1 Производные скалярных функций векторов
- 1.2 Производные вектора значные функции векторов
- 1.3 Производные скалярных функций от тензоров второго порядка
- 1.4 Производные от тензорных функций от тензоров второго порядка
- 2 Градиент тензорного поля
- 2.1 Декартовы координаты
- 2.2 Криволинейные координаты
- 2.2.1 Цилиндрические полярные координаты
- 3 Дивергенция тензорного поля
- 3.1 Декартовы координаты
- 3.2 Криволинейные координаты
- 3.2.1 Цилиндрические полярные координаты
- 4 Завихрение тензора поле
- 4.1 Ротор тензорного (векторного) поля первого порядка
- 4.2 Ротор второго порядка тензорное поле
- 4.3 Тождества, содержащие ротор тензорного поля
- 5 Производная детерминанта тензора второго порядка
- 6 Производные инвариантов тензора второго порядка
- 7 Производная второго тензор идентичности порядка
- 8 Производная тензора второго порядка относительно самого себя
- 9 Производная, обратная тензору второго порядка
- 10 Интегрирование по частям
- 11 См. также
- 12 Ссылки
Производные по векторам и тензоры второго порядка
Определения производных по направлениям для различных ситуаций приведены ниже. Предполагается, что функции достаточно гладкие, чтобы можно было брать производные.
Производные скалярнозначных функций векторов
Пусть f (v ) будет вещественной функцией вектора v . Тогда производная f (v ) относительно v (или в v ) - это вектор, определенный через его скалярное произведение с любой вектор u
![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v})[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd4359c84cf58e41375f33503df17f688456372)
для всех векторов и . Вышеупомянутое скалярное произведение дает скаляр, и если u является единичным вектором, дает производную f по направлению в v в направлении u .
Свойства:
- Если
 , затем
, затем 
- Если
 затем
затем 
- Если
 затем
затем 
Производные векторных функций векторов
Пусть f(v) будет векторной функцией вектора v . Тогда производная от f(v) по v (или по v ) - это тензор второго порядка, определенный через его скалярное произведение с любым вектором u быть
![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v})[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b946f4d0b2712f1f6b890f4b5b45a2bb70b7c7)
для всех векторов u . Приведенное выше скалярное произведение дает вектор, и если u является единичным вектором, дает производную по направлению от f в v в направленных свойствах u.
:
- Если
 , затем
, затем 
- Если
 , затем
, затем 
- Если
 тогда
тогда 
Производные скалярных функций от тензоров второго порядка
Пусть  быть вещественной функцией тензора второго порядка
быть вещественной функцией тензора второго порядка  . Тогда производная от
. Тогда производная от  по
по  (или в
(или в  ) в направлении
) в направлении  - тензор второго порядка, определяемый как
- тензор второго порядка, определяемый как
![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97c637955623ac4900c4f80d6ea1bdef354076a)
для всех тензоров второго порядка  .
.
Свойства:
- Если
 затем
затем 
- Если
 тогда
тогда 
- Если
 тогда
тогда 
Производные тензорнозначных функций от тензоров второго порядка
Пусть  быть тензорнозначной функцией второго порядка от тензора второго порядка
быть тензорнозначной функцией второго порядка от тензора второго порядка  . Тогда производная от
. Тогда производная от  по
по  (или в
(или в  ) в направлении
) в направлении  - это тензор четвертого порядка, определенный как
- это тензор четвертого порядка, определенный как
![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c53f2457fa27a03ca72cbd48debb1255593088)
для всех тензоров второго порядка  .
.
Свойства:
- Если
 , затем
, затем 
- Если
 тогда
тогда 
- Если
 затем
затем 
- Если
 затем
затем 
Градиент тензорного поля
градиент,  тензорного поля
тензорного поля  в направлении произвольного постоянного вектора c определяется как:
в направлении произвольного постоянного вектора c определяется как:

Градиент тензорного поля порядка n является тензорным полем порядка n + 1.
Декартовы координаты
- Примечание: соглашение Эйнштейна о суммировании суммирования повторяющихся индексов используется ниже.
Если  - базисные векторы в декартовой координате системе с координатами точек, обозначенными (
- базисные векторы в декартовой координате системе с координатами точек, обозначенными ( ), затем градиент тензорное поле
), затем градиент тензорное поле  определяется как
определяется как

Поскольку базисные векторы не меняются в декартовой системе координат, мы имеем следующее отношения для градиентов скалярного поля  , векторного поля v и тензорного поля второго порядка
, векторного поля v и тензорного поля второго порядка  .
.

Криволинейный координаты
- Примечание: ниже используется соглашение Эйнштейна о суммировании суммирования повторяющихся индексов.
Если  являются контравариантами базисные векторы в системе криволинейных координат с координатами точек, обозначенными (
являются контравариантами базисные векторы в системе криволинейных координат с координатами точек, обозначенными ( ), то градиент тензорного поля
), то градиент тензорного поля  определяется как ( см. доказательство.)
определяется как ( см. доказательство.)

Из этого определения мы получаем следующие соотношения для градиентов скалярного поля  , векторное поле v и тензорное поле второго порядка
, векторное поле v и тензорное поле второго порядка  .
.

где символ Кристоффеля  определяется с помощью
определяется с помощью

Цилиндрические полярные координаты
В цилиндрических координатах градиент задается как
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad {\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad {\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad {\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dac8a7176f71ff5f55be4fb2abe9bfa6df0eba71)
Дивергенция тензорного поля
дивергенция тензорное поле  определяется с помощью рекурсивного отношения
определяется с помощью рекурсивного отношения

где c - произвольный постоянный вектор, а v - векторное поле. Если  - тензорное поле порядка n>1, то дивергенция поля - это тензор порядка n - 1.
- тензорное поле порядка n>1, то дивергенция поля - это тензор порядка n - 1.
Декартовы координаты
- Примечание: соглашение Эйнштейна о суммировании суммирования повторяющихся индексов используется ниже.
В декартовой системе координат у нас есть следующие соотношения для векторного поля v и тензорное поле второго порядка  .
.

где нотация тензорного индекса для частных производных используется в крайние правые выражения. Последнее соотношение можно найти в ссылке под соотношением (1.14.13).
Согласно той же статье в случае тензорного поля второго порядка:

Важно отметить, что существуют другие письменные соглашения о расходимости тензора второго порядка. Например, в декартовой системе координат расходимость тензора второго ранга также может быть записана как

Разница заключается в том, выполняется ли дифференцирование по строкам или столбцам  и является обычным. Это демонстрируется на примере. В декартовой системе координат тензор (матрица) второго порядка
и является обычным. Это демонстрируется на примере. В декартовой системе координат тензор (матрица) второго порядка  представляет собой градиент векторной функции
представляет собой градиент векторной функции  .
.
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864380cd0a82178354a80ee58109fc0519c149ba)
Последнее уравнение эквивалентно альтернативному определению / интерпретации

Криволинейные координаты
- Примечание: ниже используется соглашение Эйнштейна о суммировании суммирования по повторяющимся индексам.
В криволинейных координатах - расходимости вектора или поле v и тензорное поле второго порядка  равны
равны

Цилиндрические полярные координаты
В цилиндрические полярные координаты
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad {\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad {\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8cd23836a8e6cc12150592c3964d95d6a3f94e9)
Завиток тензорного поля
curl тензорного поля порядка n>1  также определяется с помощью рекурсивного отношения
также определяется с помощью рекурсивного отношения

, где c - произвольный постоянный вектор, а v - векторное поле.
Curl тензорного (векторного) поля первого порядка
Рассмотрим векторное поле v и произвольный постоянный вектор c . В индексной нотации перекрестное произведение задается следующим образом:

где  - это символ перестановки, иначе известный как символ Леви-Чивита. Тогда
- это символ перестановки, иначе известный как символ Леви-Чивита. Тогда

Следовательно,

Curl тензорного поля второго порядка
Для тензора второго порядка 

Следовательно, используя определение локона первого порядка тензорное поле,

Следовательно, мы имеем

Тождества, включающие ротор тензорного поля
Наиболее часто используемые тождества, связанные с ротором тензорного поля,  , равно
, равно

Это тождество выполняется для тензорных полей всех порядков. Для важного случая тензора второго порядка,  , это тождество означает, что
, это тождество означает, что

Производная определителя тензора второго порядка
Производная определителя тензора второго порядка  задается как
задается как
![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a229cf1ec76d8d0d6c4ebf0e55e24a9289524d0f)
В ортонормированном базисе компоненты  можно записать как матрицу A . В этом случае правая часть соответствует сомножителям матрицы.
можно записать как матрицу A . В этом случае правая часть соответствует сомножителям матрицы.
Производные инвариантов тензора второго порядка
Основные инварианты тензора второго порядка:
![\begin{align} I_1(\boldsymbol{A}) = \text{tr}{\boldsymbol{A}} \\ I_2(\boldsymbol{A}) = \frac{1}{2} \left[ (\text{tr}{\boldsymbol{A}})^2 - \text{tr}{\boldsymbol{A}^2} \right] \\ I_3(\boldsymbol{A}) = \det(\boldsymbol{A}) \end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)
Производные этих трех инвариантов по  :
:
![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19cf1ad5bce9774bf510c8818f4b90e32c4f2640)
| Доказательство |
|---|
Из производной определителя мы знаем, что ![{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9dd4a16751516c5e316be643e40ce0babf1c1df)
Для производных двух других инвариантов вернемся к характеристическому уравнению 
Используя тот же подход, что и для детерминант тензора, можно показать, что ![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be1b29969a25190e4efad41db9d76f11e8a8079)
Теперь левую часть можно разложить как ![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4ad226ea72ae236eaddfe419007ff6de53d55d)
Следовательно, ![{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3993a79ec1f95da1b9e188243300861ee7ee2e45)
или, ![{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/782fb846f7870890e72cda9dbeba6e80dfc064b0)
Раскрытие правой части и разделение членов в левой части дает ![{\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9d08c98dc866bcc330678342ca3c391da0042a)
или, ![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6174aae82fa111cbe2235a21c275bb7bc0e243b4)
Если мы определим  и и  , мы можем записать это как , мы можем записать это как ![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8169e3ea8470a718a349e0d8a73e1fb7c162914)
Сбор терминов, содержащих различные степени из λ, получаем 
Затем, вызывая произвольное Если λ, то 
Это означает, что 
|
Производная тензора идентичности второго порядка
Пусть  будет тензором идентичности второго порядка. Тогда производная этого тензора по тензору второго порядка
будет тензором идентичности второго порядка. Тогда производная этого тензора по тензору второго порядка  дается выражением
дается выражением

Это потому, что  не зависит от
не зависит от  .
.
Производная тензора второго порядка относительно самого себя
Пусть  - тензор второго порядка. Тогда
- тензор второго порядка. Тогда
![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)
Следовательно,

Здесь  - тензор идентичности четвертого порядка. В индексной записи относительно ортонормированного базиса
- тензор идентичности четвертого порядка. В индексной записи относительно ортонормированного базиса

Это результат означает, что

где

Следовательно, если тензор  симметричен, то производная также симметрична, и мы получаем
симметричен, то производная также симметрична, и мы получаем

где симметричный тождественный тензор четвертого порядка равен

Производная, обратная тензору второго порядка
Пусть  и
и  два тензора второго порядка, затем
два тензора второго порядка, затем

В индексной записи относительно ортонормированного базиса

У нас также есть

В индексном обозначении

Если тензор  симметричен, то
симметричен, то

| Доказательство |
|---|
Напомним, что 
Начиная с  , мы можем написать , мы можем написать 
Использование правила произведения для тензоры второго порядка ![\frac{\partial }{\partial \boldsymbol{S}}[\boldsymbol{F}_1(\boldsymbol{S})\cdot\boldsymbol{F}_2(\boldsymbol{S})]:\boldsymbol{T} = \left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)\cdot\boldsymbol{F}_2 + \boldsymbol{F}_1\cdot\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a25e5e0ee3f8a2f287da104d5f72d8342899b9)
получаем 
или, 
Следовательно, 
|
Интеграция по частям
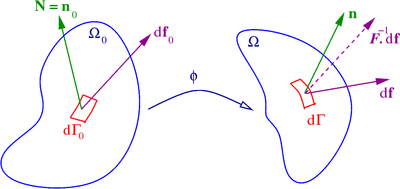
Домен

, его граница

и нормаль внешней единицы

Другой важной операцией, связанной с тензорными производными в механике сплошных сред, является интегрирование по частям. Формулу интегрирования по частям можно записать как

где  и
и  - дифференцируемые тензорные поля произвольного порядка,
- дифференцируемые тензорные поля произвольного порядка,  - единица внешней нормали к области, в которой определены тензорные поля,
- единица внешней нормали к области, в которой определены тензорные поля,  представляет оператор обобщенного тензорного произведения, а
представляет оператор обобщенного тензорного произведения, а  - это обобщенный оператор градиента. Когда
- это обобщенный оператор градиента. Когда  равно тензору идентичности, мы получаем теорему о расходимости
равно тензору идентичности, мы получаем теорему о расходимости

Мы можем выразить формулу интегрирования по частям в декартовой записи индекса как

Для особого случая, когда операция тензорного произведения является сжатием одного индекса, а операция градиента - дивергенцией, и обе  и
и  - тензоры второго порядка, мы имеем
- тензоры второго порядка, мы имеем

В индексных обозначениях

См. Также
Ссылки
![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v})[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd4359c84cf58e41375f33503df17f688456372)
 , затем
, затем 
 затем
затем 
 затем
затем 
![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v})[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b946f4d0b2712f1f6b890f4b5b45a2bb70b7c7)
 , затем
, затем 
 , затем
, затем 
 тогда
тогда 






![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97c637955623ac4900c4f80d6ea1bdef354076a)

 затем
затем 
 тогда
тогда 
 тогда
тогда 






![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c53f2457fa27a03ca72cbd48debb1255593088)

 , затем
, затем 
 тогда
тогда 
 затем
затем 
 затем
затем 



















![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad {\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad {\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad {\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dac8a7176f71ff5f55be4fb2abe9bfa6df0eba71)










![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864380cd0a82178354a80ee58109fc0519c149ba)



![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad {\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad {\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8cd23836a8e6cc12150592c3964d95d6a3f94e9)














![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a229cf1ec76d8d0d6c4ebf0e55e24a9289524d0f)

![\begin{align} I_1(\boldsymbol{A}) = \text{tr}{\boldsymbol{A}} \\ I_2(\boldsymbol{A}) = \frac{1}{2} \left[ (\text{tr}{\boldsymbol{A}})^2 - \text{tr}{\boldsymbol{A}^2} \right] \\ I_3(\boldsymbol{A}) = \det(\boldsymbol{A}) \end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)

![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19cf1ad5bce9774bf510c8818f4b90e32c4f2640)






![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)
















 Домен
Домен  , его граница
, его граница  и нормаль внешней единицы
и нормаль внешней единицы 












