Curl (математика)

Оператор, описывающий вращение в точке в трехмерном векторном поле

В векторном исчислении, curl является векторным оператором , который описывает бесконечно малое вращение векторного поля в трех -мерное евклидово пространство. В каждой точке поля изгиб этой точки представлен вектором . Атрибуты этого вектора (длина и направление) характеризуют поворот в этой точке.

Направление изгиба - это ось вращения, как определено правилом правой руки, а величина изгиба - это величина вращения. Если векторное поле представляет собой скорость потока движущейся текучей среды, то завихрение представляет собой циркуляционную плотность текучей среды. Векторное поле, ротор которого равен нулю, называется безвихревым. Curl - это форма дифференцирования для векторных полей. Соответствующая форма основной теоремы исчисления - это теорема Стокса, которая связывает поверхностный интеграл ротора векторного поля с линией . интеграл векторного поля вокруг граничной кривой.

Альтернативная терминология вращение или вращение и альтернативные обозначения rot F и ∇ × F часто используются (первое, особенно во многих европейских странах, второе, с использованием оператор del (или набла) и перекрестное произведение , больше используется в других странах) для curl F.

В отличие от градиента и дивергенции, curl не обобщается просто на другие измерения; некоторые обобщения возможны, но только в трех измерениях геометрически определенный ротор векторного поля снова является векторным полем. Это явление аналогично трехмерному перекрестному произведению , и связь отражена в обозначении ∇ × для локона.

Название «завиток» было впервые предложено Джеймсом Клерком Максвеллом в 1871 году, но, по-видимому, впервые эта концепция была использована при построении теории оптического поля Джеймсом МакКуллагом в 1839 г.

• 1 Определение
  • 1.1 Интуитивная интерпретация
• 2 Использование
• 3 Примеры
  • 3.1 Пример 1
  • 3.2 Пример 2
  • 3.3 Описательные примеры
• 4 Идентичности
• 5 Обобщения
  • 5.1 Дифференциальные формы
  • 5.2 Геометрическое изгибание
• 6 Инверсия
• 7 См. Также
• 8 Ссылки
• 9 Источники
• 10 Внешние ссылки

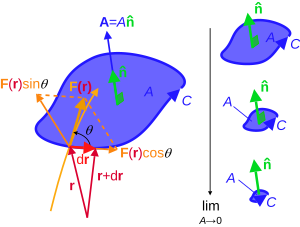Компоненты F в позиции r, нормальные и касательные к замкнутой кривой C на плоскости, охватывающей плоскую векторную область $A\; =\; A\; n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; =\; A\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$.

Ротор векторного поля F, обозначаемый curl F, или ∇ × F, или rot F, в точке определяется в терминах ее проекции на различные прямые, проходящие через точку. Если $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$- любой единичный вектор, проекция локона F на $n\; ^\; \{\; \backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$определяется как предельное значение замкнутого линейного интеграла в плоскости, ортогональной $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$делится на заключенную область, так как путь интегрирования сужается вокруг точки.

Оператор rot переводит непрерывно дифференцируемые функции f: ℝ → в непрерывные функции g: ℝ →, и, в частности, он отображает C функций в ℝ в C-функции в.

Соглашение о векторной ориентации линейного интеграла

Неявно определяется curl:

$(\nabla \; \times \; F)\; (p)\; \cdot \; n\; ^\; =\; def\; lim\; A\; \to \; 0\; (1\; |\; A\; |\; \oint \; C\; \; F\; \cdot \; dr)\; \{\backslash \; displaystyle\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\})\; (p)\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \backslash \; \{\backslash \; overset\; \{\backslash \; underset\; \{\backslash \; mathrm\; \{def\}\}\; \{\}\}\; \{=\}\; \}\; \backslash \; lim\; \_\; \{A\; \backslash \; to\; 0\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{|\; A\; |\}\}\; \backslash \; oint\; \_\; \{C\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; d\; \backslash \; mathbf\; \{r\}\; \backslash \; right)\}$

где ∮ CF⋅ d r - линейный интеграл вдоль границы рассматриваемой области области, и | A | - величина площади. Это уравнение определяет проекцию изгиба F на $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$, где $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$- вектор нормали к поверхности, ограниченной C; и C определяется через правило правой руки (см. диаграмму).

Правило правой руки для ориентации кривой. Большой палец указывает в направлении $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\}$, а пальцы сгибаются в направлении C.

Формула выше означает, что ротор векторного поля определяется как бесконечно малая плотность площади циркуляции этого поля. Этому определению, естественно,

• соответствует теорема Кельвина – Стокса как глобальная формула, соответствующая определению, и
• следующее «легко запоминающееся» определение ротора в криволинейном ортогональные координаты, например в декартовых координатах, сферических, цилиндрических или даже эллиптических или параболических координатах :

$(curl\; \; F)\; 1\; =\; 1\; h\; 2\; h\; 3\; (\partial \; (h\; 3\; F\; 3)\; \partial \; u\; 2\; -\; \partial \; (h\; 2\; F\; 2)\; \partial \; u\; 3),\; (curl\; \; F)\; 2\; =\; 1\; h\; 3\; h\; 1\; (\partial \; (h\; 1\; F\; 1)\; \partial \; u\; 3\; -\; \partial \; (h\; 3\; F\; 3)\; \partial \; u\; 1),\; (curl\; \; F)\; 3\; =\; 1\; h\; 1\; h\; 2\; (\partial \; (h\; 2\; F\; 2)\; \partial \; u\; 1\; -\; \partial \; (h\; 1\; F\; 1)\; \partial \; u\; 2).).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; (\backslash \; operatorname\; \{curl\}\; \backslash \; mathbf\; \{F\})\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{1\}\; \{h\_\; \{2\}\; h\_\; \{3\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{3\}\; F\_\; \{3\})\}\; \{\backslash \; partial\; u\_\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{2\}\; F\_\; \{2\})\}\; \{\backslash \; partial\; u\_\; \{3\}\}\}\; \backslash \; right),\; \backslash \backslash \; [5pt]\; (\backslash \; operatorname\; \{curl\}\; \backslash \; mathbf\; \{F\})\; \_\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{h\_\; \{3\}\; h\_\; \{1\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{1\}\; F\_\; \{1\})\}\; \{\backslash \; partial\; u\_\; \{3\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{3\}\; F\_\; \{3\})\}\; \{\backslash \; partial\; u\_\; \{1\}\}\}\; \backslash \; right),\; \backslash \backslash \; [5pt]\; (\backslash \; operatorname\; \{curl\}\; \backslash \; mathbf\; \{F\})\; \_\; \{3\}\; =\; \{\backslash \; frac\; \{1\}\; \{h\_\; \{1\}\; h\_\; \{2\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{2\}\; F\_\; \{2\})\}\; \{\backslash \; partial\; u\_\; \{1\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; (h\_\; \{1\}\; F\_\; \{1\})\}\; \{\backslash \; partial\; u\_\; \{2\}\}\}\; \backslash \; right).\; \backslash \; end\; \{align\}\}\}$

Уравнение для каждого компонента (curl F)kможет быть получено заменой каждого вхождения нижнего индекса 1, 2, 3 в циклической перестановке: 1 → 2, 2 → 3, и 3 → 1 (где нижние индексы представляют соответствующие индексы).

If (x 1, x 2, x 3) - декартовы координаты и (u 1, u 2, u 3) - ортогональные координаты, тогда

$hi\; =\; (\partial \; x\; 1\; \partial \; u\; я)\; 2\; +\; (\partial \; x\; 2\; \partial \; ui)\; 2\; +\; (\partial \; x\; 3\; \partial \; ui)\; 2\; \{\backslash \; displaystyle\; h\_\; \{i\}\; =\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; x\_\; \{1\}\}\; \{\backslash \; partial)\; u\_\; \{i\}\}\}\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; x\_\; \{2\}\}\; \{\backslash \; partial\; u\_\; \{i\}\}\}\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; x\_\; \{3\}\}\; \{\backslash \; partial\; u\_\; \{i\}\}\}\; \backslash \; right)\; ^\; \{2\}\}\}\}$

- длина вектора координат, соответствующего u i. Остальные два компонента curl являются результатом циклической перестановки индексов : 3,1,2 → 1,2,3 → 2,3,1.

Интуитивная интерпретация

Предположим, векторное поле описывает поле скорости потока жидкости (например, большой резервуар с жидкостью или газ ), а небольшой шарик находится внутри жидкости или газа (центр шарика закреплен в определенной точке). Если шар имеет шероховатую поверхность, жидкость, протекающая мимо него, заставит его вращаться. Ось вращения (ориентированная согласно правилу правой руки) указывает в направлении завитка поля в центре мяча, а угловая скорость вращения составляет половину величины завитка в этой точке.

Ротор вектора в любой точке задается вращением бесконечно малой области в плоскости xy (для компонента локона по оси z), плоскости zx (для компонента по оси y в изгибе) и yz-plane (для компонента оси x вектора локона). Это хорошо видно на примерах ниже.

На практике приведенное выше определение используется редко, потому что практически во всех случаях оператор curl может применяться с использованием некоторого набора криволинейных координат, для которого получены более простые представления.

Обозначение ∇ × F происходит от сходства с трехмерным перекрестным произведением, и его можно использовать как мнемонику в декартовых координатах, если ∇ взят как вектор дифференциальный оператор del. Такая запись, включающая операторы, обычна в физике и алгебре.

Расширенный в 3-мерных декартовых координатах (см. Del в цилиндрических и сферические координаты для сферических и цилиндрических координатных представлений), ∇ × F для F состоит из [F x, F y, F z ]:

$\nabla \; \times \; F\; =\; |\; ı\; ^\; ȷ\; ^\; k\; ^\; \partial \; \partial \; x\; \partial \; \partial \; y\; \partial \; \partial \; z\; F\; x\; F\; y\; F\; z\; |\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; =\; \{\backslash \; begin\; \{vmatrix\}\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; imath\}\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; шляпа\; \{k\}\}\}\; \backslash \backslash \; [5pt]\; \{\backslash \; dfrac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\}\}\; \{\backslash \; dfrac\; \{\backslash \; partial\}\; \{\backslash \; partial\; y\}\}\; и\; \{\backslash \; dfrac\; \{\backslash \; partial\}\; \{\backslash \; partial\; z\; \}\}\; \backslash \backslash \; [10pt]\; F\_\; \{x\}\; F\_\; \{y\}\; F\_\; \{z\}\; \backslash \; end\; \{vmatrix\}\}\}$

где i, jи k - это единичные векторы для осей x, y и z соответственно. Это расширяется следующим образом:

$\nabla \; \times \; F\; =\; (\partial \; F\; z\; \partial \; y\; -\; \partial \; F\; y\; \partial \; z)\; ı\; ^\; +\; (\partial \; F\; x\; \partial \; z\; -\; \partial \; F\; z\; \partial \; x)\; ȷ\; ^\; +\; (\partial \; F\; y\; \partial \; x\; -\; \partial \; F\; x\; \partial \; y)\; k\; ^\; =\; [\partial \; F\; z\; \partial \; y\; -\; \partial \; F\; y\; \partial \; z\; \partial \; F\; x\; \partial \; z\; -\; \partial \; F\; z\; \partial \; x\; \partial \; F\; y\; \partial \; x\; -\; \partial \; F\; x\; \partial \; y]\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{z\}\}\; \{\backslash \; partial\; y\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{y\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \; right)\; \{\; \backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; imath\}\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{x\}\}\; \{\backslash \; partial\; z\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{z\}\}\; \{\backslash \; partial\; x\}\}\; \backslash \; right)\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{x\}\}\; \{\backslash \; частичный\; y\}\}\; \backslash \; right)\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{k\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{z\}\}\; \{\backslash \; partial\; y\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{y\}\}\; \{\backslash \; partial\; z\}\}\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{x\}\}\; \{\backslash \; partial\; z\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{z\}\}\; \{\backslash \; partial\; x\}\}\; \backslash \backslash \; \{\; \backslash \; frac\; \{\backslash \; partial\; F\_\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; -\; \{\backslash \; frac\; \{\backslash \; partial\; F\_\; \{x\}\}\; \{\backslash \; partial\; y\}\}\; \backslash \; end\; \{bmatrix\}\}\}$

Хотя выражается в координатах, результат инвариантен при правильном повороте осей координат, но результат инвертируется при отражении ион.

В общей системе координат изгиб задается формулой

$(\nabla \; \times \; F)\; k\; =\; \epsilon \; k\; \ell \; m\; \nabla \; \ell \; F\; m\; \{\backslash \; displaystyle\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\})\; ^\; \{k\}\; =\; \backslash \; varepsilon\; ^\; \{k\; \backslash \; ell\; m\}\; \backslash \; nabla\; \_\; \{\backslash \; ell\}\; F\_\; \{m\}\}$

где ε обозначает тензор Леви-Чивиты, а ∇ ковариантная производная, метрический тензор используется для понижения индекса на F, а соглашение о суммировании Эйнштейна подразумевает, что повторяющиеся индексы подытожил. В декартовой системе координат ковариантная производная сводится к частной производной. Эквивалентно,

$(\nabla \; \times \; F)\; =\; ek\; \epsilon \; К\; \ell \; м\; \nabla \; l\; F\; m\; \{\backslash \; displaystyle\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\})\; =\; \backslash \; mathbf\; \{e\}\; \_\; \{k\}\; \backslash \; varepsilon\; ^\; \{k\; \backslash \; ell\; m\}\; \backslash \; nabla\; \_\; \{l\}\; F\_\; \{m\}\}$

где ek- координатные векторные поля. Эквивалентно, используя внешнюю производную, локон можно выразить как:

$\nabla \; \times \; F\; =\; (\star \; (d\; F\; ♭))\; ♯\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; left\; (\backslash \; star\; \{\backslash \; big\; (\}\; \{\backslash \; mathrm\; \{d\}\}\; F\; ^\; \{\backslash \; flat\}\; \{\backslash \; big)\}\; \backslash \; right)\; ^\; \{\backslash \; sharp\}\}$

Здесь ♭ и ♯ - музыкальные изоморфизмы, а ★ - это звездный оператор Ходжа. Эта формула показывает, как вычислить ротор F в любой системе координат и как расширить ротор до любого ориентированного трехмерного риманова многообразия. Поскольку это зависит от выбора ориентации, curl - это операция киральной. Другими словами, если ориентация меняется на противоположную, то направление завивки также меняется на противоположное.

Пример 1

Возьмем векторное поле :

$F\; (x,\; y,\; z)\; =\; y\; ı\; ^\; -\; x\; ȷ\; ^.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; (x,\; y,\; z)\; =\; y\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; imath\}\}\}\; -\; x\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}.\}$

Для ясности, это можно разложить следующим образом:

$F\; x\; =\; y,\; F\; y\; =\; -\; x,\; F\; z\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{x\}\; =\; y,\; \backslash \; mathbf\; \{F\}\; \_\; \{y\; \}\; =\; -\; x,\; \backslash \; mathbf\; \{F\}\; \_\; \{z\}\; =\; 0.\}$

Соответствующий график:

При визуальном осмотре поле можно описать как «вращающееся». Если бы векторы поля представляли линейную силу, действующую на объекты, присутствующие в этой точке, и объект должен был быть помещен внутри поля, объект начал бы вращаться по часовой стрелке вокруг себя. Это верно независимо от того, где размещен объект.

Вычисление локона:

$\nabla \; \times \; F\; =\; 0\; ı\; ^\; +\; 0\; ȷ\; ^\; +\; (\partial \; \partial \; x\; (-\; x)\; -\; \partial \; \partial \; yy)\; k\; ^\; =\; -\; 2\; k\; ^\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; =\; 0\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; imath\}\}\}\; +\; 0\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\; \}\}\; (-\; x)\; -\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; y\}\}\; y\; \backslash \; right)\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{k\}\}\}\; =\; -\; 2\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{k\}\}\}\}$

Результирующее векторное поле, описывающее завиток, будет равномерно двигаться в отрицательном направлении z. Результаты этого уравнения совпадают с тем, что можно было бы предсказать, используя правило правой руки с использованием правой системы координат. Будучи однородным векторным полем, описанный выше объект будет иметь одинаковую интенсивность вращения независимо от того, где он находится.

График, описывающий завиток F:

примера 2

Возьмем векторное поле:

$F\; (x,\; y,\; z)\; =\; -\; x\; 2\; ȷ\; ^.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; (x,\; y,\; z)\; =\; -\; x\; ^\; \{2\}\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}.\}$

Соответствующий график:

При первоначальной проверке curl, существующий в этом графе, не будет очевиден. Однако если взять объект в предыдущем примере и поместить его в любое место на линии x = 3, сила, приложенная к правой стороне, будет немного больше, чем сила, приложенная к левой, заставляя его вращаться по часовой стрелке. Используя правило правой руки, можно предсказать, что результирующий изгиб будет прямым в отрицательном направлении z. И наоборот, если поместить на x = −3, объект будет вращаться против часовой стрелки, и правило правой руки приведет к положительному направлению z.

Вычисление ротации:

$\nabla \; \times \; F\; =\; 0\; ı\; ^\; +\; 0\; ȷ\; ^\; +\; \partial \; \partial \; x\; (-\; x\; 2)\; k\; ^\; =\; -\; 2\; x\; k\; ^.\; \{\backslash \; displaystyle\; \{\backslash \; nabla\}\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; =\; 0\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; imath\}\}\}\; +\; 0\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{\backslash \; jmath\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\}\}\; (-\; x\; ^\; \{2\})\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{k\}\}\}\; =\; -\; 2x\; \{\backslash \; boldsymbol\; \{\backslash \; hat\; \{k\}\}\}.\}$

Как и предполагалось, точки скручивания в отрицательном направлении z, когда x положительный, и наоборот. В этом поле интенсивность вращения будет больше по мере удаления объекта от плоскости x = 0.

График, описывающий завихрение F:

Описательные примеры

• В векторном поле, описывающем линейную скорости каждой части вращающегося диска, ротор имеет одинаковое значение во всех точках.
• Из четырех уравнений Максвелла два - закон Фарадея и Закон Ампера - можно компактно выразить с помощью curl. Закон Фарадея гласит, что ротор электрического поля равен скорости, противоположной скорости изменения магнитного поля, в то время как закон Ампера связывает ротор магнитного поля с током и скоростью изменения электрического поля.

.

В общем криволинейные координаты (не только в декартовых координатах), ротор перекрестного произведения векторных полей v и F можно показать как

$\nabla \; \times \; (v\; \times \; F)\; =\; ((\nabla \; \cdot \; F)\; +\; F\; \cdot \; \nabla )\; v\; -\; ((\nabla \; \cdot \; v)\; +\; v\; \cdot \; \nabla )\; F.\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{v\; \backslash \; times\; F\}\; \backslash \; right)\; =\; \{\backslash \; Big\; (\}\; \backslash \; left\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; cdot\; F\}\; \backslash \; right)\; +\; \backslash \; mathbf\; \{F\; \backslash \; cdot\; \backslash \; nabla\}\; \{\backslash \; Big)\}\; \backslash \; mathbf\; \{v\}\; -\; \{\backslash \; Big\; (\}\; \backslash \; left\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; cdot\; v\}\; \backslash \; right)\; +\; \backslash \; mathbf\; \{v\; \backslash \; cdot\; \backslash \; nabla\}\; \{\backslash \; Big)\}\; \backslash \; mathbf\; \{F\}\; \backslash .\}$

Меняя местами векторное поле v и оператор ∇, мы приходим к перекрестному произведению векторного поля на ротор векторного поля:

$v\; \times \; (\nabla \; \times \; F)\; Знак\; равно\; \nabla \; F\; (v\; \cdot \; F)\; -\; (v\; \cdot \; \nabla )\; F,\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{v\; \backslash \; \backslash \; times\}\; \backslash \; left\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; times\; F\}\; \backslash \; right)\; =\; \backslash \; nabla\; \_\; \{\backslash \; mathbf\; \{F\}\}\; \backslash \; left\; (\backslash \; mathbf\; \{v\; \backslash \; cdot\; F\}\; \backslash \; right)\; -\; \backslash \; left\; (\backslash \; mathbf\; \{v\; \backslash \; cdot\; \backslash \; nabla\}\; \backslash \; right)\; \backslash \; mathbf\; \{F\}\; \backslash ,\}$

где ∇ F- это обозначение индекса Фейнмана, которое учитывает только изменение, обусловленное векторным полем F (т.е. в этом случае v рассматривается как постоянное в пространстве).

Другой пример - завиток завитка векторного поля. Можно показать, что в общих координатах

$\nabla \; \times \; (\nabla \; \times \; F)\; =\; \nabla \; (\nabla \; \cdot \; F)\; -\; \nabla \; 2\; F,\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; \backslash \; left\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; times\; F\}\; \backslash \; right)\; =\; \backslash \; mathbf\; \{\backslash \; nabla\}\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; cdot\; F\})\; -\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; mathbf\; \{F\}\; \backslash ,\}$

, и это тождество определяет векторный лапласиан из F, обозначается как ∇ F.

Ротор градиента любого скалярного поля φ всегда является полем нулевого вектора

$\nabla \; \times \; (\nabla \; \phi )\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; (\backslash \; nabla\; \backslash \; varphi)\; =\; \{\backslash \; boldsymbol\; \{0\}\}\}$

, что следует из антисимметрии в определении ротора и симметрии вторых производных.

Если φ - скалярная функция, а F - векторное поле, то

$\nabla \; \times \; (\phi \; F)\; =\; \nabla \; \phi \; \times \; F\; +\; \phi \; \nabla \; \times \; F\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; times\; (\backslash \; varphi\; \backslash \; mathbf\; \{F\})\; =\; \backslash \; nabla\; \backslash \; varphi\; \backslash \; times\; \backslash \; mathbf\; \{F\}\; +\; \backslash \; varphi\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{F\}\}$

Операции векторного исчисления для grad, curl и div проще всего выполнить. Это делается в контексте дифференциальных форм, что включает в себя ряд шагов. Короче говоря, они соответствуют производным от 0-форм, 1-форм и 2-форм соответственно. Геометрическая интерпретация curl как вращения соответствует идентификации бивекторов (2-векторов) в трех измерениях с помощью специальной ортогональной алгебры Ли $,\; поэтому\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{so\}\; \}\}$(3) бесконечно малых поворотов (в координатах, кососимметричных матриц 3 × 3), в то время как представление поворотов векторами соответствует идентификации 1-векторов (эквивалентно 2-векторам) и $,\; поэтому\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{so\}\}\}$(3), все это трехмерные пространства.

Дифференциальные формы

В трех измерениях дифференциальная 0-форма - это просто функция f (x, y, z); дифференциальная 1-форма - это следующее выражение:

$a\; 1\; d\; x\; +\; a\; 2\; d\; y\; +\; a\; 3\; d\; z;\; \{\backslash \; displaystyle\; a\_\; \{1\}\; \backslash ,\; dx\; +\; a\_\; \{2\}\; \backslash ,\; dy\; +\; a\_\; \{3\}\; \backslash ,\; dz;\}$

дифференциальная 2-форма - это формальная сумма:

$a\; 12\; dx\; \wedge \; dy\; +\; a\; 13\; dx\; \wedge \; dz\; +\; a\; 23\; dy\; \wedge \; dz;\; \{\backslash \; displaystyle\; a\_\; \{12\}\; \backslash ,\; dx\; \backslash \; wedge\; dy\; +\; a\_\; \{13\}\; \backslash ,\; dx\; \backslash \; wedge\; dz\; +\; a\_\; \{23\}\; \backslash ,\; dy\; \backslash \; wedge\; dz;\}$

, а дифференциальная 3-форма определяется одиночный член:

$a\; 123\; dx\; \wedge \; dy\; \wedge \; dz.\; \{\backslash \; displaystyle\; a\_\; \{123\}\; \backslash ,\; dx\; \backslash \; wedge\; dy\; \backslash \; wedge\; dz.\}$

(Здесь a-коэффициенты являются действительными функциями; «произведения клина», например dx ∧ dy, можно интерпретировать как своего рода ориентированные элементы площади, dx ∧ dy = −dy ∧ dx и т. д.)

внешняя производная k-формы в ℝ определяется как (k + 1) -форма сверху - и в, если, например,

, то внешняя производная d приводит к

Внешняя производная 1-формы, следовательно, 2-формы, а 2-формы - 3-формы. С другой стороны, из-за взаимозаменяемости смешанных производных, например поскольку

$\partial \; 2\; \partial \; x\; \partial \; Y\; =\; \partial \; 2\; \partial \; y\; \partial \; x,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\}\; \{\backslash \; partial\; x\; \backslash ,\; \backslash \; partial\; y\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\}\; \{\backslash \; partial\; y\; \backslash ,\; \backslash \; partial\; x\}\},\}$

двойное применение внешней производной приводит к 0.

Таким образом, обозначая пространство k-форм через Ω (ℝ) и внешней производной по d получается последовательность:

$0\; ⟶\; d\; \Omega \; 0\; (R\; 3)\; ⟶\; d\; \Omega \; 1\; (R\; 3)\; ⟶\; d\; \Omega \; 2\; (R\; 3)\; ⟶\; d\; \Omega \; 3\; (R\; 3)\; ⟶\; d\; 0.\; \{\backslash \; displaystyle\; 0\; \backslash ,\; \{\backslash \; overset\; \{d\}\; \{\backslash \; longrightarrow\}\}\; \backslash ,\; \backslash \; Omega\; ^\; \{0\}\; (\backslash \; mathbf\; \{R\}\; ^\; \{3\})\; \backslash ,\; \{\backslash \; overset\; \{d\}\; \{\backslash \; longrightarrow\}\}\; \backslash ,\; \backslash \; Omega\; ^\; \{1\}\; (\backslash \; mathbf\; \{R\}\; ^\; \{3\})\; \backslash ,\; \{\backslash \; overset\; \{d\}\; \{\backslash \; longrightarrow\}\}\; \backslash ,\; \backslash \; Omega\; ^\; \{2\}\; (\backslash \; mathbf\; \{R\}\; ^\; \{3\})\; \backslash ,\; \{\backslash \; overset\; \{d\}\; \{\backslash \; longrightarrow\}\}\; \backslash ,\; \backslash \; Omega\; ^\; \{3\}\; (\backslash \; mathbf\; \{R\}\; ^\; \{3\})\; \backslash ,\; \{\backslash \; overset\; \{d\}\; \{\backslash \; longrightarrow\}\}\; \backslash ,\; 0.\}$

Здесь Ω (ℝ) - пространство сечений внешней алгебры Λ (ℝ) векторного расслоения над ℝ, размерность которого является биномом коэффициент (. k); обратите внимание, что Ω (ℝ) = 0 для k>3 или k < 0. Writing only dimensions, one obtains a row of треугольник Паскаля :

0 → 1 → 3 → 3 → 1 → 0;

одномерные слои соответствуют скалярным полям, а 3 -мерные слои в векторные поля, как описано ниже. По модулю подходящих отождествлений три нетривиальных вхождения внешней производной соответствуют grad, curl и div.

Дифференциальные формы и дифференциал могут быть определены на любом евклидовом пространстве или на любом многообразии без какого-либо понятия римановой метрики. На римановом многообразии или, в более общем смысле, псевдоримановом многообразии k-формы можно отождествить с k-векторными полями (k-формы являются k-ковекторными поля, а псевдориманова метрика дает изоморфизм между векторами и ковекторами), а в ориентированном векторном пространстве с невырожденной формой (изоморфизм между векторами и ковекторами) существует изоморфизм между k-векторами и (n - k) -векторы; в частности, на (касательном пространстве) ориентированного псевдориманова многообразия. Таким образом, на ориентированном псевдоримановом многообразии можно менять местами k-формы, k-векторные поля, (n - k) -формы и (n - k)-векторные поля; это известно как двойственность Ходжа. Конкретно, на ℝ это задается:

• 1-формами и 1-векторными полями: 1-форма a x dx + a y dy + a z dz соответствует векторному полю (a x, a y, a z).
• 1-формы и 2-формы: один заменяет dx на двойную величину dy ∧ dz (т. е. опускаем dx), а также с учетом ориентации: dy соответствует dz ∧ dx = −dx ∧ dz, а dz соответствует dx ∧ dy. Таким образом, форма a x dx + a y dy + a z dz соответствует «двойной форме» a z dx ∧ dy + a y dz ∧ dx + a x dy ∧ dz.

Таким образом, идентифицируя 0-формы и 3-формы со скалярными полями, а 1-формы и 2-формы с векторными полями:

• grad принимает скалярное поле (0- form) в векторное поле (1-форма);
• curl переводит векторное поле (1-форму) в псевдовекторное поле (2-форма);
• div принимает псевдовекторное поле ( 2-форма) в псевдоскалярное поле (3-форма)

С другой стороны, тот факт, что d = 0 соответствует тождествам

$\nabla \; \times \; (\nabla \; f)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; раз\; (\backslash \; nabla\; f)\; =\; 0\}$

для любого скалярного поля f и

$\nabla \; \cdot \; (\nabla \; \times \; v)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{v\})\; =\; 0\}$

для любого векторного поля v.

Grad и div обобщают на все ориентированные псевдоримановы многообразия с той же геометрической интерпретацией, потому что пространства 0-форм и n-форм всегда (послойно) одномерны и можно отождествить со скалярными полями, тогда как пространства 1-форм и (n - 1) -форм всегда послойно n-мерны и могут быть отождествлены с векторными полями.

Curl не обобщает таким образом до 4 или более измерений (или до 2 или менее измерений); в 4-мерном измерении размерности равны

0 → 1 → 4 → 6 → 4 → 1 → 0;

так что ротор 1-векторного поля (послойно 4-мерный) является 2-векторным полем, которое послойно 6-мерное,

, что дает сумму шести независимых членов и не может быть отождествлено с 1-векторным полем. Также нельзя осмысленно перейти от 1-векторного поля к 2-векторному полю к 3-векторному полю (4 → 6 → 4), поскольку двойное взятие дифференциала дает ноль (d = 0). Таким образом, не существует ротационной функции из векторных полей в векторные поля в других измерениях, возникающих таким образом.

Однако можно определить ротор векторного поля как 2-векторное поле в целом, как описано ниже.

Изгиб геометрически

2-вектора соответствуют внешней мощности ΛV; при наличии внутреннего продукта в координатах это кососимметричные матрицы, которые геометрически рассматриваются как специальная ортогональная алгебра Ли $,\; поэтому\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{so\}\}\}$(V) бесконечно малых вращений. Это имеет (. 2)= 1 / 2n (n - 1) размерностей и позволяет интерпретировать дифференциал 1-векторного поля как его бесконечно малые вращения. Только в трех измерениях (или тривиально в 0 измерениях) n = 1 / 2n (n - 1), что является наиболее элегантным и распространенным случаем. В двух измерениях ротор векторного поля является не векторным полем, а функцией, так как двухмерные вращения задаются углом (скаляр - требуется ориентация, чтобы выбрать, считать ли вращения по часовой стрелке или против часовой стрелки положительными); это не div, а скорее перпендикулярно ему. В 3-х измерениях ротор векторного поля является известным векторным полем (в 1 и 0 измерениях ротор векторного поля равен 0, потому что нет нетривиальных 2-векторов), в то время как в 4-х измерениях ротор Геометрически векторное поле представляет собой элемент 6-мерной алгебры Ли $,\; поэтому\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{so\}\}\}$(4).

Ротор трехмерного векторного поля, который зависит только от двух координат (скажем, x и y), является просто вертикальным векторным полем (в направлении z), величина которого является завитком 2-мерного вектора. поле, как в примерах на этой странице.

Рассмотрение curl как 2-векторного поля (антисимметричный 2-тензор) было использовано для обобщения векторного исчисления и связанной с ним физики на более высокие измерения.

В случай, когда дивергенция векторного поля V равна нулю, тогда существуют векторные поля W такие, что curl (W ) = V.

If W - одно векторное поле с curl (W ) = V, тогда добавление любого градиентного векторного поля grad (f) к W приведет к другому векторное поле W + grad (f) такое, что curl (W + grad (f)) также = V . Резюмируя это, можно сказать, что обратный rot трехмерного векторного поля может быть получен с точностью до постоянной интегрирования и неизвестного безвихревого поля с помощью Закон Био – Савара.

• Перекрестное произведение
• Del
• Дивергенция
• Градиент
• Разложение Гельмгольца
• Del в цилиндрических и сферических координатах
• Завихренность

• Арфкен, Джордж Б. и Ханс Дж. Вебер. Математические методы для физиков, Academic Press; Выпуск 6 (21 июня 2005 г.). ISBN 978-0-12-059876-2.
• Корн, Гранино Артур и Тереза ​​М. Корн (январь 2000 г.). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Нью-Йорк: Dover Publications. Стр. 157 –160. ISBN 0-486-41147-8.
• Шей, Х. М. (1997). Div, Grad, Curl и все такое: неформальный текст о векторном исчислении. Нью-Йорк: Нортон. ISBN 0-393-96997-5.

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Идея ротации векторного поля
• Curl BetterExplained
• «Дивергенция и локон: язык уравнений Максвелла, поток жидкости и многое другое». 3Синий1Коричневый. 21 июня 2018 г. - через YouTube.