Геодезические Шварцшильда

Пути частиц в решении Шварцшильда уравнений поля Эйнштейна

В общей теории относительности, Геодезические Шварцшильда описывают движение частиц бесконечно малой массы в гравитационном поле центральной фиксированной массы $M\; \{\backslash \; textstyle\; M\}$. Геодезические Шварцшильда сыграли решающую роль в проверке теории Эйнштейна общей теории относительности. Например, они обеспечивают точные предсказания аномальной прецессии планет Солнечной системы и отклонения света под действием силы тяжести.

Геодезические Шварцшильда относятся только к движению частиц бесконечно малой массы $m\; \{\backslash \; textstyle\; m\}$, то есть частиц, которые сами по себе не вносят вклад в гравитационное поле. Однако они обладают высокой точностью при условии, что $m\; \{\backslash \; textstyle\; m\}$во много раз меньше центральной массы $M\; \{\backslash \; textstyle\; M\}$, например, для планет, вращающихся вокруг своего Солнца. Геодезические Шварцшильда также являются хорошим приближением к относительному движению двух тел произвольной массы при условии, что масса Шварцшильда $M\; \{\backslash \; textstyle\; M\}$установлена ​​равной сумме двух отдельных масс $m\; 1\; \{\backslash \; textstyle\; m\_\; \{1\}\}$и $m\; 2\; \{\backslash \; textstyle\; m\_\; \{2\}\}$. Это важно для предсказания движения двойных звезд в общей теории относительности.

• 1 Исторический контекст
• 2 Метрика Шварцшильда
• 3 Орбиты тестовых частиц
• 4 Локальные и запаздывающие скорости
• 5 Точное решение с использованием эллиптических функций
  • 5.1 Ньютоновский предел
  • 5.2 Корни и обзор возможных орбит
• 6 Прецессия орбит
• 7 Искривление света под действием силы тяжести
• 8 Отношение к ньютоновской физике
  • 8.1 Эффективная радиальная потенциальная энергия
  • 8.2 Круговые орбиты и их стабильность
  • 8.3 Прецессия эллиптических орбит
• 9 Математический вывод орбитального уравнения
  • 9.1 Символы Кристоффеля
  • 9.2 Геодезическое уравнение
  • 9.3 Лагранжевый подход
  • 9.4 Гамильтонов подход
  • 9.5 Подход Гамильтона – Якоби
  • 9.6 Принцип Гамильтона
    • 9.6.1 Движение по долготе
    • 9.6.2 Движение во времени
    • 9.6.3 Сохраненные импульсы
    • 9.6.4 Радиальное движение
• 10 См. Также
• 11 Примечания
• 12 Ссылки
• 13 Библиография
• 14 Внешние ссылки

Метрика Шварцшильда названа в честь своего первооткрывателя Карл Шварцшильд, который нашел решение в 1915 году, всего через месяц после публикации общей теории относительности Эйнштейна. Это было первое точное решение уравнений поля Эйнштейна, отличное от тривиального решения в плоском пространстве.

Точное решение уравнений поля Эйнштейна - это Метрика Шварцшильда, которая соответствует внешнему гравитационному полю незаряженного, невращающегося сферически-симметричного тела массы $M\; \{\backslash \; textstyle\; M\}$. Решение Шварцшильда можно записать как

$c\; 2\; d\; \tau \; 2\; =\; (1\; -\; rsr)\; c\; 2\; dt\; 2\; -\; dr\; 2\; 1\; -\; rsr\; -\; r\; 2\; d\; \theta \; 2\; -\; r\; 2\; sin\; 2\; \; \theta \; d\; \phi \; 2\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; \{d\; \backslash \; tau\}\; ^\; \{2\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; dt\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{dr\; ^\; \{2\}\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; -\; r\; ^\; \{2\}\; d\; \backslash \; theta\; ^\; \{2\}\; -r\; ^\; \{\; 2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash ,\; d\; \backslash \; varphi\; ^\; \{2\}\}$

где

$\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$- собственное время (время, измеренное часами движется вместе с частицей) в секундах,

$c\; \{\backslash \; displaystyle\; c\}$- скорость света в метрах в секунду,

$t\; \{\backslash \; displaystyle\; t\}$- временная координата (время, измеренное стационарными часами на бесконечности) в секундах,

$r\; \{\backslash \; displaystyle\; r\}$- радиальная координата (длина окружности круга с центром в разделенной звезде на $2\; \pi \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\}$) в метрах,

$\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$- это широта (угол от севера) в радианах,

$\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$- это долгота в радианах, а

$rs\; \{\backslash \; displaystyle\; r\_\; \{s\}\}$- это радиус Шварцшильда массивного тела (в метрах), который связан с его массой $M\; \{\backslash \; textstyle\; M\}$по

$rs\; =\; 2\; GM\; c\; 2,\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; =\; \{\backslash \; frac\; \{2GM\}\; \{c\; ^\; \{2\}\}\; \},\}$

где $G\; \{\backslash \; textstyle\; G\}$- гравитационная постоянная. Классическая ньютоновская теория гравитации восстанавливается в пределе, когда отношение $r\; s\; r\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\_\; \{s\}\}\; \{r\}\}\}$стремится к нулю. В этом пределе метрика возвращается к метрике, определенной в специальной теории относительности.

. На практике это отношение почти всегда чрезвычайно мало. Например, радиус Шварцшильда $r\; s\; \{\backslash \; textstyle\; r\_\; \{s\}\}$Земли составляет примерно 9 мм (⁄ 8 дюйма); на поверхности Земли поправки к ньютоновской гравитации составляют лишь одну часть на миллиард. Радиус Солнца по Шварцшильду намного больше, примерно 2953 метра, но на его поверхности отношение $rsr\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\_\; \{s\}\}\; \{r\}\}\}$примерно 4 части на миллион. Белый карлик звезда намного плотнее, но даже здесь соотношение на ее поверхности составляет примерно 250 частей на миллион. Отношение становится большим только вблизи сверхплотных объектов, таких как нейтронные звезды (где соотношение составляет примерно 50%) и черные дыры.

Сравнение орбиты пробной частицы в пространстве-времени Ньютона (слева) и Шварцшильда (справа); обратите внимание на апсидальную прецессию справа.

Мы можем упростить задачу, используя симметрию, чтобы исключить одну переменную из рассмотрения. Поскольку метрика Шварцшильда симметрична относительно $\theta \; =\; \pi \; 2\; \{\backslash \; textstyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$, любая геодезическая, которая начинает двигаться в этой плоскости, останется в эта плоскость бесконечно (плоскость полностью геодезическая ). Поэтому мы ориентируем систему координат так, чтобы орбита частицы лежала в этой плоскости, и фиксируем координату $\theta \; \{\backslash \; textstyle\; \backslash \; theta\}$как $\pi \; 2\; \{\backslash \; textstyle\; \{\; \backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$, так что метрика (этой плоскости) упрощается до

$c\; 2\; d\; \tau \; 2\; =\; (1\; -\; rsr)\; c\; 2\; dt\; 2\; -\; dr\; 2\; 1\; -\; rsr\; -\; r\; 2\; d\; \phi \; 2.\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; d\; \backslash \; tau\; ^\; \{2\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; dt\; ^\; \{2\; \}\; -\; \{\backslash \; frac\; \{dr\; ^\; \{2\}\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; -\; r\; ^\; \{2\}\; d\; \backslash \; varphi\; ^\; \{2\}.\}$

Две константы движения (значения, которые не изменяются с течением времени $\tau \; \{\backslash \; displaystyle\; \backslash \; tau\}$) могут быть идентифицированы (см. Приведенный вывод ниже). Один - это полная энергия $E\; \{\backslash \; textstyle\; E\}$:

$(1\; -\; r\; s\; r)\; d\; t\; d\; \tau \; =\; E\; m\; c\; 2.\; \{\backslash \; displaystyle\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{E\}\; \{mc\; ^\; \{2\}\}\}.\}$

, а другой - удельный угловой момент :

$h\; =\; L\; \mu \; =\; r\; 2\; d\; \phi \; d\; \tau ,\; \{\backslash \; displaystyle\; h\; =\; \{\backslash \; frac\; \{L\}\; \{\backslash \; mu\; \}\}\; =\; r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\},\}$

где L - полный угловой момент двух тел, а $\mu \; \{\backslash \; textstyle\; \backslash \; mu\}$- приведенная масса. Когда $M\; \gg \; m\; \{\backslash \; textstyle\; M\; \backslash \; gg\; m\}$, приведенная масса приблизительно равна $m\; \{\backslash \; textstyle\; m\}$. Иногда предполагается, что $m\; =\; \mu \; \{\backslash \; textstyle\; m\; =\; \backslash \; mu\}$. В случае планеты Меркурий это упрощение вносит ошибку, более чем в два раза большую, чем релятивистский эффект. При обсуждении геодезических $m\; \{\backslash \; textstyle\; m\}$можно считать вымышленным, и важны константы $E\; m\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{E\}\; \{m\}\}\}$и $h\; \{\backslash \; textstyle\; h\}$. Чтобы охватить все возможные геодезические, нам необходимо рассмотреть случаи, в которых $E\; m\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{E\}\; \{m\}\}\}$бесконечно (что дает траектории фотонов ) или мнимой (для тахионных геодезических). Для фотонного случая нам также необходимо указать число, соответствующее отношению двух констант, а именно $mh\; E\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{mh\}\; \{E\}\}\}$, что может быть нулевым или ненулевым действительным числом.

Подставляя эти константы в определение метрики Шварцшильда

$c\; 2\; =\; (1\; -\; rsr)\; c\; 2\; (dtd\; \tau )\; 2\; -\; 1\; 1\; -\; rsr\; (drd\; \tau )\; 2\; -\; r\; 2\; (d\; \phi \; d\; \tau )\; 2,\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\},\}$

дает уравнение движения для радиуса как функции собственного времени $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$:

$(drd\; \tau )\; 2\; =\; E\; 2\; m\; 2\; c\; 2\; -\; (1\; -\; rsr)\; (c\; 2\; +\; ч\; 2\; р\; 2).\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\; \}\}\; \backslash \; right).\}$

Формальное решение этой проблемы:

$\tau \; =\; \int \; dr\; \pm \; E\; 2\; m\; 2\; c\; 2\; -\; (1\; -\; rsr)\; (c\; 2\; +\; h\; 2\; r\; 2).\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \backslash \; int\; \{\backslash \; frac\; \{dr\}\; \{\backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1-\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; right)\; \}\}\}\}.\}$

Обратите внимание, что квадратный корень для тахионических геодезических будет мнимым.

Использование отношения выше между $dtd\; \tau \; \{\backslash \; textstyle\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\}$и $E\; \{\backslash \; textstyle\; E\}$, мы также можем записать

$t\; =\; \int \; dr\; \pm \; c\; (1\; -\; rsr)\; 1\; -\; (1\; -\; rsr)\; (c\; 2\; +\; h\; 2\; r\; 2)\; m\; 2\; c\; 2\; E\; 2.\; \{\backslash \; displaystyle\; t\; =\; \backslash \; int\; \{\backslash \; frac\; \{dr\}\; \{\backslash \; pm\; c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{1-\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\; \{E\; ^\; \{2\}\}\}\}\}\}\}.\}$

Поскольку асимптотически, подынтегральное выражение обратно пропорционально $r\; -\; rs\; \{\backslash \; textstyle\; r-r\; \_\; \{\backslash \; rm\; \{s\}\}\}$, это показывает, что в $r,\; \theta ,\; \phi ,\; t\; \{\backslash \; textstyle\; r,\; \backslash \; theta,\; \backslash \; varphi,\; t\}$рамка отсчета, если $r\; \{\backslash \; textstyle\; r\}$приближается к $rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$, он делает так экспоненциально, даже не достигнув этого. Однако как функция от $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$, $r\; \{\backslash \; textstyle\; r\}$действительно достигает $rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$.

Вышеуказанное решения действительны, пока подынтегральное выражение конечно, но полное решение может включать две или бесконечное количество частей, каждая из которых описывается интегралом, но с чередующимися знаками для квадратного корня.

Когда $E\; =\; mc\; 2\; \{\backslash \; textstyle\; E\; =\; mc\; ^\; \{2\}\}$и $h\; =\; 0\; \{\backslash \; textstyle\; h\; =\; 0\}$, мы можем явно решить для $t\; \{\backslash \; textstyle\; t\}$и $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$:

$t\; =\; constant\; \pm \; rsc\; (2\; 3\; (rrs)\; 3\; 2\; +\; 2\; rrs\; +\; ln\; \; |\; rrs\; -\; 1\; |\; rrs\; +\; 1)\; \tau \; =\; константа\; \pm \; 2\; 3\; rsc\; (rrs)\; 3\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; t\; =\; \{\backslash \; text\; \{constant\}\; \}\; \backslash \; pm\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{c\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{3\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\})\; \}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; +\; 2\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}\; +\; \backslash \; ln\; \{\backslash \; frac\; \{\backslash \; left\; |\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}\; -\; 1\; \backslash \; right\; |\}\; \{\{\backslash \; sqrt\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}\; +\; 1\}\}\; \backslash \; right)\; \backslash \backslash \backslash \; tau\; =\; \{\backslash \; text\; \{constant\}\}\; \backslash \; pm\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{c\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; end\; \{align\}\}\}$

и для фотонных геодезических ($m\; =\; 0\; \{\backslash \; textstyle\; m\; =\; 0\}$) с нулевым угловым моментом

$t\; =\; constant\; \pm \; 1\; c\; (r\; +\; rs\; ln\; \; |\; rrs\; -\; 1\; |)\; \tau \; =\; константа.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; t\; =\; \{\backslash \; text\; \{constant\}\}\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{c\}\}\; \backslash \; left\; (r\; +\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; \backslash \; ln\; \backslash \; left\; |\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; -\; 1\; \backslash \; right\; |\; \backslash \; right)\; \backslash \backslash \backslash \; tau\; =\; \{\backslash \; text\; \{constant\}\}.\; \backslash \; end\; \{align\}\}\}$

(Хотя собственное время тривиально в фотонном случае, можно определить аффинный параметр $\lambda \; \{\backslash \; textstyle\; \backslash \; lambda\}$, и тогда решение геодезического уравнения будет $r\; =\; c\; 1\; \lambda \; +\; c\; 2\; \{\backslash \; textstyle\; r\; =\; c\_\; \{1\}\; \backslash \; lambda\; +\; c\_\; \{2\}\}$.)

Другой разрешимый случай - это когда $E\; =\; 0\; \{\backslash \; textstyle\; E\; =\; 0\}$и $t\; \{\backslash \; textstyle\; t\}$и $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$являются постоянными. В объеме, где , это дает для собственного времени

$\tau \; =\; constant\; \pm \; r\; s\; c\; (arcsin\; \; r\; r\; s\; -\; r\; r\; s\; (1\; -\; r\; r\; s)).\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \{\backslash \; text\; \{constant\}\}\; \backslash \; pm\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{c\}\}\; \backslash \; left\; (\backslash \; arcsin\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}\; -\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\})\; \}\}\; \backslash \; right)\}\}\; \backslash \; right).\}$

Это близко к решениям с $E\; 2\; m\; 2\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\}\}\}$маленький и позитивный. За пределами $rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$решение $E\; =\; 0\; \{\backslash \; textstyle\; E\; =\; 0\}$тахионное, а «собственное время» пространственно-подобный:

$\tau \; =\; constant\; \pm \; irsc\; (ln\; \; (rrs\; +\; rrs\; -\; 1)\; +\; rrs\; (rrs\; -\; 1)).\; \{\backslash \; displaystyle\; \backslash \; tau\; =\; \{\backslash \; text\; \{constant\}\}\; \backslash \; pm\; i\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{c\}\}\; \backslash \; left\; (\backslash \; ln\; \backslash \; left\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{r\})\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}\; +\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; -\; 1\}\}\; \backslash \; right)\; +\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{\; r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{r\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; -\; 1\; \backslash \; right)\}\}\; \backslash \; right).\}$

Это близко к другим тахионным решениям с $E\; 2\; m\; 2\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\}\}\}$маленьким и отрицательным. Константа $t\; \{\backslash \; textstyle\; t\}$тахионная геодезическая вне $rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$не продолжается константой $t\; \{\backslash \; textstyle\; t\}$геодезическая внутри $rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$, но скорее продолжается в «параллельную внешнюю область» (см. координаты Крускала – Секереса ). Другие тахионические решения могут войти в черную дыру и повторно выйти в параллельную внешнюю область. Решение с постоянным t внутри горизонта событий ($rs\; \{\backslash \; textstyle\; r\_\; \{s\}\}$) продолжается решением с постоянным t в белой дыре.

Когда угловой момент равен отличное от нуля, мы можем заменить зависимость от собственного времени зависимостью от угла $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$, используя определение $h\; \{\backslash \; textstyle\; h\}$

$(drd\; \phi )\; 2\; знак\; равно\; (drd\; \tau )\; 2\; (d\; \tau \; d\; \phi )\; 2\; =\; (drd\; \tau )\; 2\; (r\; 2\; час)\; 2,\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\; \}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{h\}\}\; \backslash \; right)\; ^\; \{2\},\}$

, что дает уравнение для орбиты

$(drd\; \phi )\; 2\; =\; r\; 4\; b\; 2\; -\; (1\; -\; rsr)\; (r\; 4\; a\; 2\; +\; r\; 2)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{b\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\})\; \}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{a\; ^\; \{2\}\}\}\; +\; r\; ^\; \{2\}\; \backslash \; right)\}$

где, для краткости, две длины - шкалы, $a\; \{\backslash \; textstyle\; a\}$и $b\; \{\; \backslash \; textstyle\; b\}$, были определены как

$a\; =\; h\; c,\; b\; =\; c\; L\; E\; =\; h\; m\; c\; E.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; a\; =\; \{\backslash \; frac\; \{h\}\; \{c\}\},\; \backslash \backslash \; b\; =\; \{\backslash \; frac\; \{cL\}\; \{E\}\}\; =\; \{\backslash \; frac\; \{hmc\}\; \{E\}\}.\; \backslash \; end\; \{align\}\}\}$

Обратите внимание, что в тахионическом случае $a\; \{\backslash \; textstyle\; a\}$будет воображаемым, а $b\; \{\backslash \; textstyle\; b\}$реальным или бесконечно.

Это же уравнение также может быть получено с использованием лагранжевого подхода или уравнения Гамильтона – Якоби (см. ниже). Решение уравнения орбиты:

$\phi \; =\; \int \; d\; r\; \pm \; r\; 2\; 1\; b\; 2\; -\; (1\; -\; r\; s\; r)\; (1\; a\; 2\; +\; 1\; r\; 2).\; \{\backslash \; displaystyle\; \backslash \; varphi\; =\; \backslash \; int\; \{\backslash \; frac\; \{dr\}\; \{\backslash \; pm\; r\; ^\; \{2\}\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{b\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{\; r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; right)\}\}\}\}.\}$

Это может быть выражено в терминах эллиптической функции Вейерштрасса $\wp \; \{\backslash \; textstyle\; \backslash \; wp\}$.

В отличие от классической механики, в координатах Шварцшильда $drd\; \tau \; \{\backslash \; textstyle\; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; r\}\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; tau\}\}\}$и $rd\; \phi \; d\; \tau \; \{\backslash \; textstyle\; r\; \backslash \; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; varphi\}\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; tau\}\}\}$не являются радиальными $v\; \parallel \; \{\backslash \; textstyle\; v\; \_\; \{\backslash \; parallel\}\}$и поперечный $v\; \perp \; \{\backslash \; textstyle\; v\; \_\; \{\backslash \; perp\}\}$компоненты локальной скорости $v\; \{\backslash \; textstyle\; v\}$(относительно неподвижного наблюдателя), вместо этого они дают компоненты для скорости, которые связаны с $v\; \{\backslash \; textstyle\; v\; \}$от

$drd\; \tau \; =\; v\; \parallel \; 1\; -\; rsr\; \gamma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; r\}\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; tau\}\}\; =\; v\_\; \{\backslash \; parallel\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; \backslash \; gamma\}$

для радиального и

$d\; \phi \; d\; \tau \; =\; v\; \perp \; r\; \gamma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; varphi\}\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{v\; \_\; \{\backslash \; perp\}\}\; \{r\}\}\; \backslash \; \backslash \; gamma\}$

для поперечного компонента движения, с $v\; 2\; =\; v\; \parallel \; 2\; +\; v\; \perp \; 2\; \{\backslash \; textstyle\; v\; ^\; \{2\}\; =\; v\; \_\; \{\backslash \; parallel\}\; ^\; \{2\}\; +\; v\; \_\; \{\backslash \; perp\}\; ^\; \{2\}\}$. Счетчик координат вдали от сцены наблюдает задержку по Шапиро скорость $v\; ^\; \{\backslash \; textstyle\; \{\backslash \; hat\; \{v\}\}\}$, которая задается соотношением

$v\; ^\; \perp \; =\; v\; \perp \; 1\; -\; rsr\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{v\}\}\; \_\; \{\backslash \; perp\}\; =\; v\; \_\; \{\backslash \; perp\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; \}\; \{r\}\}\}\}\}$и $v\; ^\; \parallel \; =\; v\; \parallel \; (1\; -\; rsr)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{v\}\}\; \_\; \{\backslash \; parallel\}\; =\; v\; \_\; \{\backslash \; parallel\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\}$.

Коэффициент замедления времени между бухгалтером и движущейся тестовой частицей также можно представить в виде

$d\; \tau \; dt\; =\; 1\; -\; rsr\; \gamma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; rm\; \{d\}\}\; \backslash \; tau\}\; \{\{\backslash \; rm\; \{d\}\}\; t\}\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \{\backslash \; gamma\}\}\}$

где числитель - гравитационный, а знаменатель - кинематический компонент замедления времени. Для частицы, падающей из бесконечности, левый коэффициент равен правому, поскольку скорость падения $v\; \{\backslash \; textstyle\; v\}$соответствует космической скорости $crsr\; \{\backslash \; textstyle\; c\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}$в этом случае.

Две константы углового момента $L\; \{\backslash \; textstyle\; L\}$и полная энергия $E\; \{\backslash \; textstyle\; E\}$пробной частицы с масса $m\; \{\backslash \; textstyle\; m\}$в терминах $v\; \{\backslash \; textstyle\; v\}$

$L\; =\; mv\; \perp \; r\; \gamma \; \{\backslash \; displaystyle\; L\; =\; m\; \backslash \; v\; \_\; \{\backslash \; perp\}\; \backslash \; r\; \backslash \; \backslash \; gamma\}$

и

$E\; =\; mc\; 2\; 1\; -\; rsr\; \gamma \; \{\backslash \; displaystyle\; E\; =\; mc\; ^\; \{2\}\; \backslash \; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \}\; \{r\}\}\}\}\; \backslash \; \backslash \; gamma\}$

где

$E\; =\; E\; rest\; +\; E\; kin\; +\; E\; pot\; \{\backslash \; displaystyle\; E\; =\; E\; \_\; \{\backslash \; rm\; \{rest\}\}\; +\; E\; \_\; \{\backslash \; rm\; \{kin\}\}\; +\; E\; \_\; \{\backslash \; rm\; \{pot\}\}\}$

и

$E\; rest\; =\; mc\; 2,\; E\; kin\; =\; (\gamma \; -\; 1)\; mc\; 2,\; E\; pot\; =\; (1\; -\; rsr\; -\; 1)\; \gamma \; mc\; 2\; \{\backslash \; displaystyle\; E\; \_\; \{\backslash \; rm\; \{rest\}\}\; =\; mc\; ^\; \{2\}\; \backslash ,\; \backslash \; \backslash \; E\; \_\; \{\backslash \; rm\; \{kin\}\}\; =\; (\backslash \; gamma\; -1)\; mc\; ^\; \{2\}\; \backslash ,\; \backslash \; \backslash \; E\; \_\; \{\backslash \; rm\; \{pot\}\}\; =\; \backslash \; left\; (\{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; -\; 1\; \backslash \; right)\; \backslash \; \backslash \; gamma\; \backslash \; mc\; ^\; \{2\}\}$

Для массивных тестовых частиц $\gamma \; \{\backslash \; textstyle\; \backslash \; gamma\}$- фактор Лоренца $\gamma \; =\; 1/1\; -\; v\; 2\; /\; c\; 2\; \{\backslash \; textstyle\; \backslash \; gamma\; =\; 1\; /\; \{\backslash \; sqrt\; \{1-v\; ^\; \{2\}\; /\; c\; ^\; \{2\}\}\}\}$и $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$- это собственное время, в то время как для безмассовых частиц, таких как фотоны $\gamma \; \{\backslash \; textstyle\; \backslash \; gamma\}$, установлено в $1\; \{\backslash \; textstyle\; 1\}$и $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$играет роль аффинного параметра. Если частица безмассовая $E\; rest\; \{\backslash \; textstyle\; E\; \_\; \{\backslash \; rm\; \{rest\}\}\}$заменяется на $E\; kin\; \{\backslash \; textstyle\; E\; \_\; \{\backslash \; rm\; \{kin\}\}\}$и $mc\; 2\; \{\backslash \; textstyle\; mc\; ^\; \{2\}\}$с $hf\; \{\backslash \; textstyle\; hf\}$, где $h\; \{\backslash \; textstyle\; h\}$- это постоянная Планка, а $f\; \{\backslash \; textstyle\; f\}$- локально наблюдаемая частота.

Основное уравнение орбиты легче решить, если оно выражено через обратный радиус $u\; =\; 1\; r\; \{\backslash \; textstyle\; u\; =\; \{\backslash \; frac\; \{1\}\; \{r\}\}\}$

$(dud\; \phi )\; 2\; =\; 1\; b\; 2\; -\; (1\; -\; urs)\; (1\; a\; 2\; +\; u\; 2)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{du\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{b\; ^\; \{2\}\}\; \}\; -\; \backslash \; left\; (1-ur\; \_\; \{\backslash \; rm\; \{s\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{a\; ^\; \{2\}\}\}\; +\; u\; ^\; \{2\}\; \backslash \; right)\}$

Правая часть этого уравнения - кубический многочлен, который имеет три корня, обозначенные здесь как u 1, u 2 и u 3

$(\; неудачник\; \phi )\; 2\; знак\; равно\; rs\; (U\; -\; U\; 1)\; (U\; -\; U\; 2)\; (U\; -\; U\; 3)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{du\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; \backslash \; left\; (u-u\_\; \{1\}\; \backslash \; right)\; \backslash \; left\; (u-u\_\; \{2\}\; \backslash \; right)\; \backslash \; left\; (u-u\_\; \{3\}\; \backslash \; right)\}$

Сумма трех корней равный коэффициенту члена u

$u\; 1\; +\; u\; 2\; +\; u\; 3\; =\; 1\; rs\; \{\backslash \; displaystyle\; u\_\; \{1\}\; +\; u\_\; \{2\}\; +\; u\_\; \{3\}\; =\; \{\backslash \; frac\; \{1\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}$

Кубический многочлен с действующими средствами может иметь три настоящих корня или Действительный корен ь и два комплексно-сопряженных корня . Если все три корня являются действительными числами, корни помечаются так, что u 1< u2< u3. Если вместо этого существует только один действительный корень, то он обозначается как u 3 ; комплексно сопряженные корни обозначены u 1 и u 2. Используя правило знаков Декарта, может быть не более одного отрицательного корня; u 1 отрицательно тогда и только тогда, когда b < a. As discussed below, the roots are useful in determining the types of possible orbits.

Учитывая такое обозначение корней, решение фундаментального орбитального уравнения будет

$u\; =\; u\; 1\; +\; (u\; 2\; -\; u\; 1)\; sn\; 2\; (1\; 2\; \phi \; RS\; (U\; 3\; -\; U\; 1)\; +\; \delta )\; \{\backslash \; Displaystyle\; u\; =\; u\_\; \{1\}\; +\; \backslash \; left\; (u\_\; \{2\}\; -u\_\; \{1\}\; \backslash \; right)\; \backslash ,\; \backslash \; mathrm\; \{sn\}\; ^\; \{2\}\; \backslash \; left\; (\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; varphi\; \{\backslash \; sqrt\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; \backslash \; left\; (u\_\; \{3\}\; -u\_\; \{1\}\; \backslash \; right)\}\}\; +\; \backslash \; delta\; \backslash \; right)\}$

где sn представляет синусоидальную амплитудную функцию (одна из эллиптических функций Якоби ), а δ - постоянная интегрирования, отражающее начальное положение. эллиптический модуль k этой эллиптической функции задается формулой

$k\; =\; u\; 2\; -\; u\; 1\; u\; 3\; -\; u\; 1\; \{\backslash \; displaystyle\; k\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{u\_\; \{2\})\; -u\_\; \{1\; \}\}\; \{u\_\; \{3\}\; -u\_\; \{1\}\}\}\}\}$

Ньютоновский предел

Чтобы восстановить ньютоновское решение для планетных орбитов, предел как радиус Шварцшильда r s обнуляется. В этом случае третий корень u 3 становится примерно $1\; rs\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\}\}$, и намного больше, чем u 1 или u 2. Следовательно, модуль k стремится к нулю; в этом пределе sn становится тригонометрической функцией синуса

$u\; =\; u\; 1\; +\; (u\; 2\; -\; u\; 1)\; sin\; 2\; \; (1\; 2\; \phi \; +\; \delta )\; \{\backslash \; displaystyle\; u\; =\; u\_\; \{1\}\; +\; \backslash \; left\; (u\_\; \{2\}\; -u\_\; \{1\}\; \backslash \; right)\; \backslash ,\; \backslash \; sin\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; varphi\; +\; \backslash \; delta\; \backslash \; right)\}$

В соответствии с решениями Ньютона для планетных движений эта формула указанной фокусной конику эксцентриситета e

$e\; =\; u\; 2\; -\; u\; 1\; u\; 2\; +\; u\; 1\; \{\backslash \; displaystyle\; e\; =\; \{\backslash \; frac\; \{u\_\; \{2\}\; -u\_\; \{1\}\}\; \{u\_\; \{2\}\; +\; u\_\; \{1\}\}\}\}$

Если u 1 - положительное действующее число, то орбитаительное представляет собой эллипс, где u 1 и u 2 количество меньшего и большего сближения, соответственно. Если u 1 равно нулю или отрицательному действительному существованию, орбита является параболой или гиперболой соответственно. В этих двух последних случаях u 2 представляет собой наибольшее сближение; поскольку орбита уходит в бесконечность (u = 0), дальнего сближения нет.

Корни и обвиняемый орбит

Корень представляет собой точку орбиты, где производная обращается в нуль, т.е. где $dud\; \varphi \; =\; 0\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{du\}\; \{d\; \backslash \; phi\}\}\; =\; 0\}$. В такой формуной точке u достигает максимума, минимума или точки перегиба в зависимости от значения второй производной, которая задаетсялой

$d\; 2\; ud\; \phi \; 2\; =\; rs\; 2\; [(u\; -\; u\; 2)\; (u\; -\; u\; 3)\; +\; (u\; -\; u\; 1)\; (u\; -\; u\; 3)\; +\; (u\; -\; u\; 1)\; (u\; -\; u\; 2)]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; u\}\; \{d\; \backslash \; varphi\; ^\; \{2\}\}\}\; =\; \{\backslash \; гидроразрыва\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{2\}\}\; \backslash \; left\; [\backslash \; left\; (u-u\_\; \{2\}\; \backslash \; right)\; \backslash \; left\; (u-u\_\; \{3\}\; \backslash \; right)\; +\; \backslash \; left\; (u-u\_\; \{1\}\; \backslash \; right)\; \backslash \; left\; (u-u\_\; \{3\}\; \backslash \; right)\; +\; \backslash \; left\; (u-u\_\; \{1\}\; \backslash \; right)\; \backslash \; left\; (u-u\_\; \{2\}\; \backslash \; right)\; \backslash \; right]\}$

Если все три корня являются различными действующими числами, вторая производная будет положительной, отрицательной и положительной в u 1,u2и u 3 соответственно. Отсюда следует, что график зависимости u от φ может колебаться между u 1 и u 2, или он может перемещаться от u 3 в сторону бесконечности (что соответствует к г стремится к нулю). Если u 1 отрицательно, произойдет только часть «колебания». Это соответствует частице, исходящей из бесконечности, приближающейся к бесконечности, а затем снова удаляющейся к бесконечности, подобной гиперболической траектории в классическом решении.

Если части ее обладает достаточным мощностью для углового момента, u 2 и u 3 сольются. В этом случае есть три решения. Орбита может закручиваться по спирали до $r\; =\; 1\; u\; 2\; =\; 1\; u\; 3\; \{\backslash \; textstyle\; r\; =\; \{\backslash \; frac\; \{1\}\; \{u\_\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{u\_\; \{3\}\}\}\; \}$, приближаясь к этому радиусу как (асимптотически) убывающая экспонента по φ, τ или t. Или можно иметь круговую орбиту с этим радиусом. Или можно иметь орбиту, которая движется по спирали от этого радиуса иметь к центральной точке. Рассматриваемый радиус называется внутренним радиусом и находится между $3\; 2\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{3\}\; \{2\}\}\}$и трехкратным r s. Круговая орбита также возникает, когда u 2 равно u 1, и это происходит как происходит. Эти различные типы орбит обсуждаются ниже.

Если частица приходит в центральную массу с достаточной энергией и низким угловым моментом, тогда только u 1 будет действительным. Это соответствует падению частиц в черную дыру. Орбита закручивается по спирали с конечным изменением φ.

Функция sn и ее квадрат sn имеют периоды 4K и 2K соответственно, где K определяется уравнением

$K\; =\; \int \; 0\; 1\; dy\; (1\; -\; Y\; 2)\; (1\; -\; К\; 2\; Y\; 2)\; \{\backslash \; Displaystyle\; К\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{dy\}\; \{\backslash \; sqrt\; \{\backslash \; left\; (1-y\; ^\; \{2\}\; \backslash \; right)\; \backslash \; left\; (1-k\; ^\; \{\; 2\}\; y\; ^\; \{2\}\; \backslash \; right)\}\}\}\}$

Следовательно, изменение φ за одно колебание u (или, что то же самое, одно колебание r) равно

$\Delta \; \phi \; знак\; равно\; 4\; К\; RS\; (u\; 3\; -\; u\; 1)\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; varphi\; =\; \{\backslash \; frac\; \{4K\}\; \{\backslash \; sqrt\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\; \backslash \; left\; (u\_\; \{3\}\; -u\_\; \{1\})\; \backslash \; right)\}\}\; \}\}$

В классическом пределе u 3 приближается к $1\; rs\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\}\}$и намного больше, чем u 1 или u 2. Следовательно, k приблизительно равно

$k\; 2\; =\; u\; 2\; -\; u\; 1\; u\; 3\; -\; u\; 1\; \approx \; rs\; (u\; 2\; -\; u\; 1)\; \ll \; 1\; \{\backslash \; displaystyle\; k\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{u\_\; \{2\}\; -\; u\_\; \{1\}\}\; \{u\_\; \{3\}\; -u\_\; \{1\}\}\}\; \backslash \; приблизительно\; r\; \_\; \{\backslash \; text\; \{s\}\}\; \backslash \; left\; (u\_\; \{2\}\; -u\_\; \{1\}\; \backslash \; right)\; \backslash \; ll\; 1\}$

Для по тем же причинам знаменатель Δφ равно равенству

$1\; rs\; (u\; 3\; -\; u\; 1)\; =\; 1\; 1\; -\; rs\; (2\; u\; 1\; +\; u\; 2)\; \approx \; 1\; +\; 1\; 2\; rs\; (2\; u\; 1\; +\; u\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\; \backslash \; left\; (u\_\; \{3\}\; -u\_\; \{1\}\; \backslash \; right)\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; -r\; \_\; \{\backslash \; text\; \{s\}\}\; \backslash \; left\; (2u\_\; \{1\}\; +\; u\_\; \{2\}\; \backslash \; right)\}\}\}\; \backslash \; приблизительно\; 1\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; r\; \_\; \{\backslash \; text\; \{s\}\; \}\; \backslash \; left\; (2u\_\; \{1\}\; +\; u\_\; \{2\}\; \backslash \; right)\}$

Временной модуль k близок к нулю, период K можно разложить по степеням k; в самом низком порядке это расширение дает

$K\; \approx \; \int \; 0\; 1\; dy\; 1\; -\; y\; 2\; (1\; +\; 1\; 2\; k\; 2\; y\; 2)\; =\; \pi \; 2\; (1\; +\; k\; 2\; 4)\; \{\backslash \; displaystyle\; K\; \backslash \; приблизительно\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{dy\}\; \{\backslash \; sqrt\; \{1-y\; ^\; \{2\}\}\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; k\; ^\; \{2\}\; y\; ^\; \{2\; \}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{k\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\}$

Подставляя эти приближения в формулу для Δφ дает формулу для углового повреждения на радиальном колебании

$\delta \; \phi \; =\; \Delta \; \phi \; -\; 2\; \pi \; \approx \; 3\; 2\; \pi \; rs\; (u\; 1\; +\; u\; 2)\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; =\; \backslash \; Delta\; \backslash \; varphi\; -2\; \backslash \; pi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; pi\; r\; \_\; \{\backslash \; text\; \{s\}\}\; \backslash \; left\; (u\_\; \{1\}\; +\; u\_\; \{2\}\; \backslash \; right)\}$

Для эллиптической орбиты u 1 и u 2 означает собой инверсии наибольшего и наименьшего расстоянияний соответственно. Их можно выразить через большую полуось эллипса A и его эксцентриситет орбиты e,

$r\; max\; =\; 1\; u\; 1\; =\; A\; (1\; +\; e)\; r\; min\; Знак\; равно\; 1\; U\; 2\; знак\; равно\; A\; (1\; -\; e)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; r\; \_\; \{\backslash \; text\; \{max\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{u\_\; \{1\}\}\}\; =\; A\; (1\; +\; e)\; \backslash \; \backslash \; r\; \_\; \{\backslash \; text\; \{min\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{u\_\; \{2\}\}\}\; =\; A\; (1-e)\; \backslash \; end\; \{align\}\}\}$

, что дает

$u\; 1\; +\; U\; 2\; знак\; равно\; 2\; A\; (1\; -\; е\; 2)\; \{\backslash \; displaystyle\; u\_\; \{1\}\; +\; u\_\; \{2\}\; =\; \{\backslash \; frac\; \{2\}\; \{A\; \backslash \; left\; (1-e\; ^\; \{2\}\; \backslash \; right)\}\}\}$

Подстановка определения r s дает окончательное уравнение

$\delta \; \phi \; \approx \; 6\; \pi \; GM\; c\; 2\; A\; (1\; -\; e\; 2)\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{6\; \backslash \; pi\; GM\; \}\; \{c\; ^\; \{2\}\; A\; \backslash \; left\; (1-e\; ^\; \{2\}\; \backslash \; right)\}\}\}$

Отклонение света (исходящего из места, синим) вблизи компактное тело ( показано серым)

В пределе, когда масса частиц m стремится к нулю (или что то же самое, если свет направляется прямо к центральной массе, когда масштаб длины a стремится к бесконечности) уравнение для орбиты становится

$\phi \; =\; \int \; drr\; 2\; 1\; b\; 2\; -\; (1\; -\; rsr)\; 1\; r\; 2\; \{\backslash \; displaystyle\; \backslash \; varphi\; =\; \backslash \; int\; \{\backslash \; frac\; \{dr\}\; \{r\; ^\; \{2\}\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{b\; ^\; \{2\}\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\}\}\}\}\}$

Расширение по степеням $rsr\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\; \{r\}\}\}$, член главного порядка в этой формуле дает приблизительное угловое отклонение δφ для безмассовой частицы, входящей из бесконечности и уходящей обратно в бесконечность:

$\delta \; \phi \; \approx \; 2\; rsb\; =\; 4\; GM\; c\; 2\; b.\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{2r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{b\}\}\; =\; \{\backslash \; frac\; \{4GM\}\; \{c\; ^\; \{2\}\; b\}\}.\}$

Здесь b - прицельный параметр, несколько превышающий расстояниешего сближения, r 3:

$b\; =\; r\; 3\; r\; 3\; r\; 3\; -\; rs\; \{\backslash \; displaystyle\; b\; =\; r\_\; \{3\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{r\_\; \{3\}\}\; \{r\_\; \{3\})\; -r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\}$

Хотя эта формула является приблизительной, она точна для распространения гравитационного линзирования из-за малости отношения $rsr\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\; \{r\}\}\}$. Для скользящего по поверхности солнца света приблизительное угловое отклонение составляет примерно 1,75 угловых секунд, что составляет примерно одну миллионную часть круга.

Эффективная радиальная потенциальная энергия

Уравнение движения для частиц, полученное выше

$(drd\; \tau )\; 2\; =\; E\; 2\; m\; 2\; c\; 2\; -\; с\; 2\; +\; rsc\; 2\; р\; -\; L\; 2\; м\; \mu \; р\; 2\; +\; rs\; L\; 2\; м\; \mu \; р\; 3\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; гидроразрыв\; \{\; E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; c\; ^\; \{2\}\}\; \{r\}\}\; -\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{m\; \backslash \; mu\; r\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; L\; ^\; \{2\}\}\; \{m\; \backslash \; mu\; r\; ^\; \{3\}\; \}\}\}$

можно переписать с использованием определения радиуса Шварцшильда rsкак

$1\; 2\; м\; (drd\; \tau )\; 2\; =\; [E\; 2\; 2\; mc\; 2\; -\; 1\; 2\; mc\; 2]\; +\; GM\; mr\; -\; L\; 2\; 2\; \mu \; р\; 2\; +\; г\; (M\; +\; m)\; L\; 2\; c\; 2\; \mu \; р\; 3,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\})\}\; \backslash \; справа)\; ^\; \{2\}\; =\; \backslash \; left\; [\{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{2mc\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; mc\; ^\; \{2\}\; \backslash \; right]\; +\; \{\backslash \; frac\; \{GMm\}\; \{r\}\}\; -\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{2\; \backslash \; mu\; r\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{G\; (M\; +\; m)\; L\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\; \backslash \; mu\; r\; ^\; \{3\}\}\},\}$

что эквивалентно движению частиц в одномерном эффективном ном потенциале

$V\; (r)\; =\; -\; GM\; mr\; +\; L\; 2\; 2\; \mu \; r\; 2\; -\; г\; (M\; +\; м)\; L\; 2\; с\; 2\; \mu \; р\; 3\; \{\backslash \; Displaystyle\; V\; (г)\; =\; -\; \{\backslash \; fr\; ac\; \{GMm\}\; \{r\}\}\; +\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{2\; \backslash \; mu\; r\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{G\; (M\; +\; m)\; L\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\; \backslash \; mu\; r\; ^\; \{3\}\}\}\}$

Первые два члена являются хорошо известными энергиями, первый - это притягивающая ньютоновская потенциальная энергия гравитации, второй - отталкивающий «центробежный» потенциал энергии ; однако третий член представляет собой привлекательную энергию, уникальную для общей теории относительности. Как показано ниже и в другом месте, эта обратнокубическая энергия вызывает возникшую прецессию эллиптических орбитов на угол δφ за оборот

$\delta \; \phi \; \approx \; 6\; \pi \; G\; (M\; +\; m)\; c\; 2\; A\; (1\; -\; e\; 2)\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{6\; \backslash \; pi\; G\; (M\; +\; m)\}\; \{c\; ^\; \{2\}\; A\; \backslash \; left\; (1-e\; ^\; \{2\}\; \backslash \; right)\}\}\}$

где A - большая полуось, а e - эксцентриситет.

Третий член является привлекательным и доминирует при малых значениях r, давая критический внутренний радиус r внутренний, при котором частица неумолимо втягивается внутрь до r = 0; Этот внутренний механизм является функцией углового момента частицы на единицу массы или, что то же самое, масштаба, определенного выше.

Круговые орбиты и их устойчивость

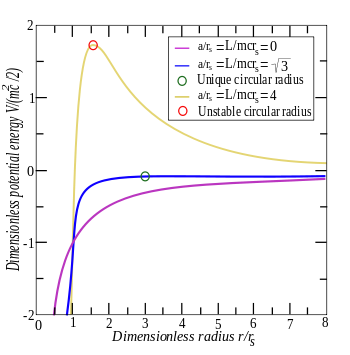
Эффективный радиальный потенциал для различных угловых моментов. На малых радиусах энергия резко падает, заставляя частицу неумолимо тянуться внутрь до r = 0. Однако, когда нормированный угловой момент $ars\; =\; L\; mcrs\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{a\}\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\}\; =\; \{\backslash \; frac\; \{L\}\; \{mcr\; \_\; \{\backslash \; text\; \{s\}\}\}\}\}$равно квадратному корню из трех, метастабильная круговая орбита возможна на радиусе, выделенном значком зеленый кружок. При более высоких угловых моментах имеется значительный центробежный барьер (оранжевая кривая) и нестабильный внутренний радиус, выделенный красным.

Эффективный потенциал V можно переписать через длину $a\; =\; hc\; \{\backslash \; textstyle\; a\; =\; \{\backslash \; frac\; \{h\}\; \{c\}\}\}$.

$V\; (r)\; =\; \mu \; c\; 2\; 2\; [-\; rsr\; +\; a\; 2\; r\; 2\; -\; rsa\; 2\; r\; 3]\; \{\backslash \; displaystyle\; V\; (r)\; =\; \{\backslash \; frac\; \{\backslash \; mu\; c\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; +\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{r\; ^\; \{\; 2\}\}\}\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; a\; ^\; \{2\}\}\; \{r\; ^\; \{3\}\}\}\; \backslash \; right]\}$

Круговые орбиты возможны, когда эффективная сила равна нулю

$F\; =\; -\; d\; V\; dr\; =\; -\; \mu \; c\; 2\; 2\; r\; 4\; [rsr\; 2\; -\; 2\; a\; 2\; r\; +\; 3\; rsa\; 2]\; =\; 0\; \{\backslash \; displaystyle\; F\; =\; -\; \{\backslash \; frac\; \{dV\}\; \{dr\}\}\; =\; -\; \{\backslash \; гидроразрыв\; \{\backslash \; mu\; c\; ^\; \{2\}\}\; \{2r\; ^\; \{4\}\}\}\; \backslash \; left\; [r\; \_\; \{\backslash \; rm\; \{s\}\}\; r\; ^\; \{2\}\; -2a\; ^\; \{2\}\; r\; +\; 3r\; \_\; \{\backslash \; rm\; \{s\}\}\; a\; ^\; \{2\}\; \backslash \; right]\; =\; 0\}$

то есть, когда две силы притяжения - ньютоновская гравитация (первый член) и притяжение, уникальное для общей теории относительности (третий член) - точно уравновешиваются центробежной силой отталкивания (второй срок). Есть два радиуса, на которых может происходить такая балансировка, обозначенные здесь как r внутренний и r внешний

$r\; внешний\; =\; a\; 2\; rs\; (1\; +\; 1\; -\; 3\; rs\; 2\; a\; 2)\; r\; внутренний\; =\; a\; 2\; rs\; (1\; -\; 1\; -\; 3\; rs\; 2\; a\; 2)\; =\; 3\; a\; 2\; r\; внешний\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; r\; \_\; \{\backslash \; text\; \{outer\}\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{3r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\}\; \backslash \; справа)\; \backslash \backslash \; [3pt]\; r\; \_\; \{\backslash \; text\; \{inner\}\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; sqrt\; \{1-\; \{\; \backslash \; frac\; \{3r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{3a\; ^\; \{2\}\}\; \{r\; \_\; \{\backslash \; text\; \{outer\}\}\}\; \}\; \backslash \; end\; \{align\}\}\}$

, которые получены с использованием квадратной формулы . Внутренний радиус r внутренний является нестабильным, поскольку третья сила притяжения усиливается намного быстрее, чем две другие силы, когда r становится малым; если частица слегка проскальзывает внутрь от r внутреннего (где все три силы уравновешены), третья сила доминирует над двумя другими и неумолимо втягивает частицу внутрь до r = 0. Однако на внешнем радиусе круговые орбиты устойчивы; третий член менее важен, и система ведет себя больше как нерелятивистская проблема Кеплера.

Когда a намного больше, чем r s (классический случай), эти формулы становятся приблизительно

$r\; внешний\; \approx \; 2\; a\; 2\; rsr\; внутренний\; \approx \; 3\; 2\; rs\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; r\; \_\; \{\backslash \; text\; \{external\}\}\; \backslash \; ок\; \{\backslash \; frac\; \{2a\; ^\; \{2\}\}\; \{r\; \_\; \{\backslash \; rm\; \{s\; \}\}\}\}\; \backslash \backslash \; [3pt]\; r\; \_\; \{\backslash \; text\; \{inner\}\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; \backslash \; end\; \{align\}\}\}$

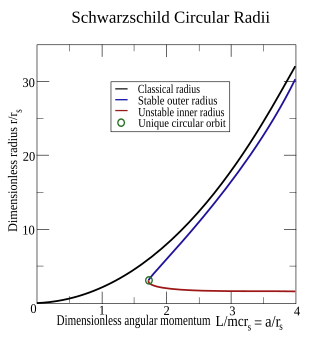
Конюшня и нестабильные радиусы построены в зависимости от нормализованного углового момента $ars\; =\; L\; mcrs\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{a\}\; \{r\; \_\; \{\backslash \; text\; \{s\}\}\}\}\; =\; \{\backslash \; frac\; \{L\}\; \{mcr\; \_\; \{\backslash \; text\; \{\; s\}\}\}\}\}$синим и красным соответственно. Эти кривые встречаются на уникальной круговой орбите (зеленый кружок), когда нормированный угловой момент равен квадратному корню из трех. Для сравнения, классический радиус, предсказанный на основе центростремительного ускорения и закона всемирного тяготения Ньютона, показан черным цветом.

Подставляя определения a и r s в r external дает классическую формулу для частицы массы m, вращающейся вокруг тела массы M.

$router\; 3\; =\; G\; (M\; +\; m)\; \omega \; \phi \; 2\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; mathrm\; \{outer\}\}\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{G\; (M\; +\; m)\}\; \{\backslash \; omega\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\}\}\}$

где ω φ - орбитальная угловая скорость частицы. Эта формула получается в нерелятивистской механике, устанавливая центробежную силу равной ньютоновской гравитационной силе:

$GM\; mr\; 2\; =\; \mu \; \omega \; \phi \; 2\; r\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{GMm\}\; \{r\; ^\; \{2\}\}\}\; =\; \backslash \; mu\; \backslash \; omega\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\; r\}$

Где $\mu \; \{\backslash \; textstyle\; \backslash \; mu\}$- приведенная масса.

В наших обозначениях классическая орбитальная угловая скорость равна

$\omega \; \phi \; 2\; \approx \; GM\; router\; 3\; =\; (rsc\; 2\; 2\; router\; 3)\; =\; (rsc\; 2\; 2)\; (rs\; 3\; 8\; a\; 6)\; =\; c\; 2\; rs\; 4\; 16\; a\; 6\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{GM\}\; \{r\; \_\; \{\backslash \; mathrm\; \{outer\}\}\; ^\; \{3\}\}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; c\; ^\; \{2\}\}\; \{2r\; \_\; \{\backslash \; mathrm\; \{outer\}\}\; ^\; \{3\}\}\}\; \backslash \; right)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; c\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{3\}\}\; \{8a\; ^\; \{6\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{c\; ^\; \{2\}\; r\_\; \{\; \backslash \; rm\; \{s\}\}\; ^\; \{4\}\}\; \{16a\; ^\; \{6\}\}\}\}$

С другой стороны, когда a приближается к 3r s сверху, два радиуса сходятся к одному значению

$router\; \approx \; rinner\; \approx \; 3\; rs\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; mathrm\; \{outer\}\}\; \backslash \; приблизительно\; r\; \_\; \{\backslash \; mathrm\; \{inner\}\}\; \backslash \; приблизительно\; 3r\; \_\; \{\backslash \; rm\; \{s\}\}\}$

Приведенные выше квадратичные решения гарантируют, что r external всегда больше 3r s, тогда как r internal находится между ⁄ 2rsи 3r с. Круговые орбиты меньше ⁄ 2rsневозможны. Для безмассовых частиц a стремится к бесконечности, подразумевая, что существует круговая орбита для фотонов при r internal = ⁄ 2rs. Сфера этого радиуса иногда известна как фотонная сфера.

Прецессия эллиптических орбит

В нерелятивистской задаче Кеплера частица следует тому же идеальному эллипсу (красная орбита) вечно. Общая теория относительности вводит третью силу, которая притягивает частицу немного сильнее, чем гравитация Ньютона, особенно на малых радиусах. Эта третья сила заставляет эллиптическую орбиту частицы прецессировать (голубую орбиту) в направлении ее вращения; этот эффект был измерен в Меркурии, Венере и Земле. Желтая точка на орбитах представляет собой центр притяжения, такой как Солнце.

Скорость орбитальной прецессии может быть получена с использованием этого радиального эффективного V. Небольшое радиальное отклонение от круговой орбиты радиусом r внешний будет стабильно колебаться с угловой частотой

$\omega \; r\; 2\; =\; 1\; м\; [d\; 2\; V\; dr\; 2]\; r\; =\; маршрутизатор\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{r\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{m\}\}\; \backslash \; left\; [\{\; \backslash \; frac\; \{d\; ^\; \{2\}\; V\}\; \{dr\; ^\; \{2\}\}\}\; \backslash \; right]\; \_\; \{r\; =\; r\; \_\; \{\backslash \; mathrm\; \{outer\}\}$

что равно

$\omega \; р\; 2\; знак\; равно\; (c\; 2\; RS\; 2\; маршрутизатор\; 4)\; (маршрутизатор\; -\; rinner)\; =\; \omega \; \phi \; 2\; 1-3\; RS\; 2\; a\; 2\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{r\}\; ^\; \{2\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{c\; ^\; \{2\}\; r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{2r\; \_\; \{\backslash \; mathrm\; \{external\}\}\; ^\; \{4\}\}\}\; \backslash \; right)\; \backslash \; left\; (r\; \_\; \{\backslash \; mathrm\; \{external\}\}\; -r\; \_\; \{\backslash \; mathrm\; \{inner\}\}\; \backslash \; справа)\; =\; \backslash \; omega\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\; \{\backslash \; sqrt\; \{1\; -\; \{\backslash \; frac\; \{3r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\}\}$

Извлечение квадратного корня из частей и выполнение разложения в ряд Тейлора дает

$\omega \; р\; знак\; равно\; \omega \; \phi \; [1-3\; rs\; 2\; 4\; a\; 2\; +\; O\; (rs\; 4\; a\; 4)]\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{r\}\; =\; \backslash \; omega\; \_\; \{\backslash \; varphi\}\; \backslash \; left\; [1-\; \{\backslash \; frac\; \{3r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{2\}\}\; \{4a\; ^\; \{2\}\}\}\; +\; \{\backslash \; mathcal\; \{O\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{4\; \}\}\; \{a\; ^\; \{4\}\}\}\; \backslash \; right)\; \backslash \; right]\}$

Умножение на период T одного оборота дает прецессию орбиты за оборот

$\delta \; \phi \; =\; T\; (\omega \; \phi \; -\; \omega \; r)\; \approx \; 2\; \pi \; (3\; рс\; 2\; 4\; a\; 2)\; знак\; равно\; 3\; \pi \; м\; 2\; с\; 2\; 2\; L\; 2\; рс\; 2\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; =\; T\; \backslash \; left\; (\backslash \; omega\; \_\; \{\backslash \; varphi\}\; -\; \backslash \; omega\; \_\; \{r\}\; \backslash \; справа)\; \backslash \; приблизительно\; 2\; \backslash \; pi\; \backslash \; left\; (\{\backslash \; frac\; \{3r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{2\}\}\; \{4a\; ^\; \{2\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{3\; \backslash \; pi\; m\; ^\; \{2\}\; c\; ^\; \{2\}\}\; \{2L\; ^\; \{2\}\}\}\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; ^\; \{2\}\}$

где мы использовали ω φ T = 2п и определение масштаб длины a. Подстановка определения радиуса Шварцшильда rsдает

$\delta \; \phi \; \approx \; 3\; \pi \; m\; 2\; c\; 2\; 2\; L\; 2\; (4\; G\; 2\; M\; 2\; c\; 4)\; =\; 6\; \pi \; G\; 2\; M\; 2\; m\; 2\; c\; 2\; L\; 2\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{3\; \backslash \; pi\; m\; ^\; \{2\}\; c\; ^\; \{2\}\}\; \{2L\; ^\; \{2\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{4G\; ^\; \{2\}\; M\; ^\; \{2\}\}\; \{c\; ^\; \{4\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{6\; \backslash \; pi\; G\; ^\; \{2\}\; M\; ^\; \{2\}\; m\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\; L\; ^\; \{2\}\; \}\}\}$

Это можно упростить, используя полуось A эллиптической орбиты и эксцентриситет e, связанные формулой

$h\; 2\; G\; (M\; +\; m)\; =\; A\; (1\; -\; e\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{G\; (M\; +\; m)\}\}\; =\; A\; \backslash \; left\; (1-e\; ^\; \{2\}\; \backslash \; right)\}$

, чтобы получить угол прецессии

$\delta \; \phi \; \approx \; 6\; \pi \; G\; (M\; +\; m)\; c\; 2\; A\; (1\; -\; e\; 2)\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; varphi\; \backslash \; приблизительно\; \{\backslash \; frac\; \{6\; \backslash \; pi\; G\; (M\; +\; m)\}\; \{c\; ^\; \{2\}\; A\; \backslash \; left\; (1-e\; ^\; \{2\}\; \backslash \; right)\}\}\}$

символы Кристоффеля

Неисчезающие символы Кристоффеля для метрики Шварцшильда равны:

$\Gamma \; rtt\; =\; -\; \Gamma \; rrr\; =\; rs\; 2\; r\; (r\; -\; rs)\; \Gamma \; ttr\; =\; rs\; (r\; -\; rs)\; 2\; r\; 3\; \Gamma \; \varphi \; \varphi \; r\; =\; (rs\; -\; r)\; sin\; 2\; \; (\theta )\; \Gamma \; \theta \; \theta \; r\; =\; rs\; -\; r\; \Gamma \; r\; \theta \; \theta \; =\; \Gamma \; р\; \varphi \; \varphi \; =\; 1\; р\; \Gamma \; \varphi \; \varphi \; \theta \; =\; -\; грех\; \; (\theta )\; соз\; \; (\theta )\; \Gamma \; \theta \; \varphi \; \varphi \; =\; детская\; кроватка\; \; (\theta )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Gamma\; \_\; \{rt\}\; ^\; \{\; t\}\; =\; -\; \backslash \; Gamma\; \_\; \{rr\}\; ^\; \{r\}\; =\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{2r\; (r-r\; \_\; \{\backslash \; rm\; \{s\}\})\}\}\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{tt\}\; ^\; \{r\}\; =\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\; (r-r\; \_\; \{\backslash \; rm\; \{s\}\})\}\; \{2r\; ^\; \{3\}\}\}\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{\backslash \; phi\; \backslash \; phi\}\; ^\; \{r\}\; =\; (r\; \_\; \{\backslash \; rm\; \{s\}\}\; -\; r)\; \backslash \; sin\; ^\; \{2\}\; (\backslash \; theta)\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{\backslash \; theta\; \backslash \; theta\; \}\; ^\; \{r\}\; =\; r\; \_\; \{\backslash \; rm\; \{s\}\}\; -\; r\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{r\; \backslash \; theta\}\; ^\; \{\backslash \; theta\}\; =\; \backslash \; Gamma\; \_\; \{r\; \backslash \; phi\}\; ^\; \{\backslash \; phi\}\; =\; \{\backslash \; frac\; \{1\}\; \{r\}\}\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{\backslash \; phi\; \backslash \; phi\}\; ^\; \{\backslash \; theta\}\; =\; -\; \backslash \; sin\; (\backslash \; theta)\; \backslash \; cos\; (\backslash \; theta)\; \backslash \backslash \; [3pt]\; \backslash \; Gamma\; \_\; \{\backslash \; theta\; \backslash \; phi\}\; ^\; \{\backslash \; phi\}\; =\; \backslash \; cot\; (\backslash \; theta)\; \backslash \; end\; \{align\}\}\}$

Геодезическое уравнение

Согласно общей теории относительности Эйнштейна, частицы пренебрежимо малое массовое путешествие по геодезическим в пространстве-времени. В плоском пространстве-времени, вдали от источника гравитации, эти геодезические соответствуют прямым линиям; однако они могут отклоняться от прямых линий, когда пространство-время искривлено. Уравнение геодезических линий:

$d\; 2\; x\; \lambda \; dq\; 2\; +\; \Gamma \; \mu \; \nu \; \lambda \; dx\; \mu \; dqdx\; \nu \; dq\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; x\; ^\; \{\backslash \; lambda\}\}\; \{dq\; ^\; \{2\}\}\}\; +\; \backslash \; Gamma\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; ^\; \{\backslash \; lambda\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\}\; \{dq\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; nu\}\}\; \{dq\}\}\; =\; 0\}$

где Γ представляет собой символ Кристоффеля, а переменная $q\; \{\backslash \; textstyle\; q\}$параметризует путь частицы через пространство-время, его так называемая мировая линия. Символ Кристоффеля зависит только от метрического тензора $g\; \mu \; \nu \; \{\backslash \; textstyle\; g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\}$, или, скорее, от того, как он изменяется с положением. Переменная $q\; \{\backslash \; textstyle\; q\}$является постоянным кратным собственному времени $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$для времениподобных орбит (которые перемещаются массивными частицами) и обычно принимается равным ему. Для светоподобных (или нулевых) орбит (которые перемещаются безмассовыми частицами, такими как фотон ) собственное время равно нулю и, строго говоря, не может использоваться в качестве переменной $q\; \{\backslash \; textstyle\; q\; \}$. Тем не менее, светоподобные орбиты могут быть получены как ультрарелятивистский предел времениподобных орбит, то есть предел, при котором масса m частицы стремится к нулю при сохранении ее полной энергии фиксированной.

Таким образом, наиболее простой способ найти движение частицы - это решить уравнение геодезических, подход, принятый Эйнштейном и другими. Метрику Шварцшильда можно записать как

$c\; 2\; d\; \tau \; 2\; =\; w\; (r)\; c\; 2\; dt\; 2\; -\; v\; (r)\; dr\; 2\; -\; r\; 2\; d\; \theta \; 2\; -\; r\; 2\; sin\; 2\; \; \theta \; d\; \varphi \; 2\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; d\; \backslash \; tau\; ^\; \{2\}\; =\; w\; (r)\; c\; ^\; \{2\}\; dt\; ^\; \{2\}\; -v\; (r)\; dr\; ^\; \{2\}\; -r\; ^\; \{2\}\; d\; \backslash \; theta\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; d\; \backslash \; phi\; ^\; \{2\}\; \backslash ,\}$

где две функции $w\; (r)\; =\; 1\; -\; rsr\; \{\backslash \; textstyle\; w\; (r)\; =\; 1\; -\; \{\backslash \; frac\; \{r\_\; \{s\}\}\; \{r\}\}\}$и его обратная величина $v\; (r)\; =\; 1\; w\; (r)\; \{\backslash \; textstyle\; v\; (r)\; =\; \{\backslash \; frac\; \{\; 1\}\; \{w\; (r)\}\}\}$определены для краткости. По этой метрике можно вычислить символы Кристоффеля $\Gamma \; \mu \; \nu \; \lambda \; \{\backslash \; textstyle\; \backslash \; Gamma\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; ^\; \{\backslash \; lambda\}\}$, и результаты подставить в уравнения геодезических

$0 = d 2 θ dq 2 + 2 rd θ dqdrdq - sin ⁡ θ cos ⁡ θ (d ϕ dq) 2 0 = d 2 ϕ dq 2 + 2 rd ϕ dqdrdq + 2 кроватки ⁡ θ d ϕ dqd θ dq 0 = d 2 tdq 2 + 1 wdwdrdtdqdrdq 0 = d 2 rdq 2 + 1 2 vdvdr (drdq) 2 - rv (d θ dq) 2 - r sin 2 ⁡ θ v (d ϕ dq) 2 + c 2 2 vdwdr ( dtdq) 2 {\ displaystyle {\ begin {align} 0 = {\ frac {d ^ {2} \ theta} {dq ^ {2}}} + {\ frac {2} {r}} {\ frac {d \ theta} {dq}} {\ frac {dr} {dq}} - \ sin \ theta \ cos \ theta \ left ({\ frac {d \ phi} {dq}} \ right) ^ {2} \\ [3pt] 0 = {\ frac {d ^ {2} \ phi} {dq ^ {2}}} + {\ frac {2} {r}} {\ frac {d \ phi} {dq}} {\ frac {dr} {dq}} + 2 \ cot \ theta {\ frac {d \ phi} {dq}} {\ frac {d \ theta} {dq}} \\ [3pt] 0 = {\ frac {d ^ {2} t} {dq ^ {2}}} + {\ frac {1} {w}} {\ frac {dw} {dr}} {\ frac {dt} {dq}} {\ frac {dr } {dq}} \\ [3pt] 0 = {\ frac {d ^ {2} r} {dq ^ {2}}} + {\ frac {1} {2v}} {\ frac {dv} {dr }} \ left ({\ frac {d r} {dq}} \ right) ^ {2} - {\ frac {r} {v}} \ left ({\ frac {d \ theta} {dq}} \ right) ^ {2} - {\ frac {r \ sin ^ {2} \ theta} {v}} \ left ({\ frac {d \ phi} {dq}} \ right) ^ {2} + {\ frac {c ^ {2}} {2v }} {\ frac {dw} {dr}} \ left ({\ frac {dt} {dq}} \ right) ^ {2} \ end {align}}}$

Можно проверить, что $\theta \; =\; \pi \; 2\; \{\backslash \; textstyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$является допустимым решением путем подстановки в первое из этих четырех уравнений. По симметрии орбита должна быть плоской, и мы можем расположить систему координат так, чтобы экваториальная плоскость была плоскостью орбиты. Это решение $\theta \; \{\backslash \; textstyle\; \backslash \; theta\}$упрощает второе и четвертое уравнения.

Чтобы решить второе и третье уравнения, достаточно разделить их на $d\; \varphi \; dq\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{dq\}\}\}$и $dtdq\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{dt\}\; \{dq\}\}\}$соответственно.

$0\; =\; ddq\; [ln\; \; d\; \varphi \; dq\; +\; ln\; \; r\; 2]\; 0\; =\; ddq\; [ln\; \; dtdq\; +\; ln\; \; w],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; 0\; =\; \{\backslash \; frac\; \{d\}\; \{dq\; \}\}\; \backslash \; left\; [\backslash \; ln\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{dq\}\}\; +\; \backslash \; ln\; r\; ^\; \{2\}\; \backslash \; right]\; \backslash \backslash \; [3pt]\; 0\; =\; \{\backslash \; frac\; \{d\}\; \{dq\}\}\; \backslash \; left\; [\; \backslash \; ln\; \{\backslash \; frac\; \{dt\}\; \{dq\}\}\; +\; \backslash \; ln\; w\; \backslash \; right],\; \backslash \; end\; \{align\}\}\}$

что дает две константы движения.

Лагранжев подход

Поскольку тестовые частицы следуют геодезическим в фиксированной метрике, орбиты этих частиц могут быть определены с использованием вариационного исчисления, также называемого лагранжевым подходом. Геодезические в пространстве-времени определяются как кривые, для которых небольшие локальные изменения в их координатах (при фиксированных конечных точках событий) не вызывают значительных изменений их общей длины s. Это можно выразить математически, используя вариационное исчисление

$0\; =\; \delta \; s\; =\; \delta \; \int \; ds\; =\; \delta \; \int \; g\; \mu \; \nu \; dx\; \mu \; d\; \tau \; dx\; \nu \; d\; \tau \; d\; \tau \; =\; \delta \; \int \; 2\; T\; d\; \tau \; \{\backslash \; displaystyle\; 0\; =\; \backslash \; delta\; s\; =\; \backslash \; delta\; \backslash \; int\; ds\; =\; \backslash \; delta\; \backslash \; int\; \{\backslash \; sqrt\; \{g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; nu\}\}\; \{d\; \backslash \; tau\}\}\}\}\; d\; \backslash \; tau\; =\; \backslash \; delta\; \backslash \; int\; \{\backslash \; sqrt\; \{2T\}\}\; d\; \backslash \; tau\}$

, где τ - собственное время, s = cτ - длина дуги в пространстве-времени, а T определяется как

$2\; T\; =\; c\; 2\; =\; (dsd\; \tau )\; 2\; =\; g\; \mu \; \nu \; dx\; \mu \; d\; \tau \; dx\; \nu \; d\; \tau \; =\; (1\; -\; rsr)\; c\; 2\; (dtd\; \tau )\; 2\; -\; 1\; 1\; -\; rsr\; (drd\; \tau )\; 2\; -\; r\; 2\; (d\; \phi \; d\; \tau )\; 2\; \{\backslash \; displaystyle\; 2T\; =\; c\; ^\; \{2\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{ds\})\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; nu\}\}\; \{\; d\; \backslash \; tau\}\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\; \}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\; \}\}\; \backslash \; right)\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\}$

по аналогии с кинетическим энергия. Если производная по собственному времени представлена ​​точкой для краткости

$x\; \dot{}\; \mu \; =\; dx\; \mu \; d\; \tau \; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{x\}\}\; ^\; \{\backslash \; mu\}\; =\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\}\; \{d\; \backslash \; tau\}\}\}$

T можно записать как

$2\; T\; =\; c\; 2\; =\; (1\; -\; rsr)\; c\; 2\; (t\; \dot{})\; 2\; -\; 1\; 1\; -\; rsr\; (r\; \dot{})\; 2\; -\; р\; 2\; (\phi \; \dot{})\; 2\; \{\backslash \; displaystyle\; 2T\; =\; c\; ^\; \{2\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; dot\; \{t\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; dot\; \{r\}\}\; \backslash \; right)\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; dot\; \{\backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\}$

Постоянные множители (например, c или квадратный корень из два) не влияют на ответ на вариационную задачу; следовательно, если взять вариацию внутрь интеграла, получим принцип Гамильтона

$0\; =\; \delta \; \int \; 2\; T\; d\; \tau \; =\; \int \; \delta \; T\; 2\; T\; d\; \tau \; =\; 1\; c\; \delta \; \int \; T\; d\; \tau .\; \{\backslash \; displaystyle\; 0\; =\; \backslash \; delta\; \backslash \; int\; \{\backslash \; sqrt\; \{2T\}\}\; d\; \backslash \; tau\; =\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; delta\; T\}\; \{\backslash \; sqrt\; \{2T\}\}\}\; d\; \backslash \; tau\; =\; \{\backslash \; frac\; \{1\}\; \{c\; \}\}\; \backslash \; delta\; \backslash \; int\; Td\; \backslash \; tau.\}$

Решение вариационной задачи дается уравнениями Лагранжа

$dd\; \tau \; (\partial \; T\; \partial \; x\; \dot{}\; \sigma )\; =\; \partial \; T\; \partial \; x\; \sigma .\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{d\; \backslash \; tau\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; \{\backslash \; dot\; \{x\}\}\; ^\; \{\backslash \; sigma\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; T\}\; \{\backslash \; partial\; x\; ^\; \{\backslash \; sigma\}\}\}.\}$

В применении к t и φ эти уравнения показывают две константы движения

$dd\; \tau \; [r\; 2\; d\; \phi \; d\; \tau \; ]\; =\; 0,\; дд\; \tau \; [(1\; -\; rsr)\; dtd\; \tau ]\; =\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{d\}\; \{d\; \backslash \; tau\}\}\; \backslash \; left\; [r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right]\; =\; 0,\; \backslash \backslash \; \{\backslash \; frac\; \{d\}\; \{d\; \backslash \; tau\}\}\; \backslash \; left\; [\backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\; \}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right]\; =\; 0,\; \backslash \; end\; \{align\}\}\}$

что может быть выражено через две постоянные длины - шкалы, $a\; \{\backslash \; textstyle\; a\}$и $b\; \{\backslash \; textstyle\; b\}$

$r\; 2\; d\; \phi \; d\; \tau \; =\; ac,\; (1\; -\; rsr)\; dtd\; \tau \; =\; ab.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; =\; ac,\; \backslash \backslash \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\})\; \}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{a\}\; \{b\}\}.\; \backslash \; end\; \{align\}\}\}$

Как показано выше, замена этих уравнений в определение метрики Шварцшильда дает уравнение для орбиты.

Гамильтонов подход

Лагранжево решение может быть преобразовано в эквивалентную гамильтонову форму. В этом случае гамильтониан $H\; \{\backslash \; displaystyle\; H\}$определяется как

$2\; H\; =\; c\; 2\; =\; pt\; 2\; c\; 2\; (1\; -\; rsr)\; -\; (1\; -\; rsr)\; pr\; 2\; -\; п\; \theta \; 2\; р\; 2\; -\; п\; \phi \; 2\; р\; 2\; грех\; 2\; \; \theta \; \{\backslash \; displaystyle\; 2H\; =\; c\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{p\_\; \{t\}\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; p\_\; \{r\}\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{p\; \_\; \{\backslash \; theta\}\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{p\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\}\; \{r\; ^\; \{2\; \}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}\}$

Опять же, орбита может быть ограничена $\theta \; =\; \pi \; 2\; \{\backslash \; textstyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$по симметрии. Поскольку $t\; \{\backslash \; textstyle\; t\}$и $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$не появляются в гамильтониане, их сопряженные импульсы постоянны; они могут быть выражены в терминах скорости света $c\; \{\backslash \; textstyle\; c\}$и двух постоянных масштабов длины $a\; \{\backslash \; textstyle\; a\}$и $b\; \{\backslash \; textstyle\; b\}$

$p\; \phi \; =\; -\; acp\; \theta \; =\; 0\; pt\; =\; ac\; 2\; b\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; p\; \_\; \{\backslash \; varphi\}\; =\; -\; ac\; \backslash \backslash \; p\; \_\; \{\backslash \; theta\}\; =\; 0\; \backslash \backslash \; p\_\; \{t\}\; =\; \{\backslash \; frac\; \{ac\; ^\; \{2\}\}\; \{b\}\}\; \backslash \; end\; \{align\}\}\}$

Производные по собственному времени даются как

$drd\; \tau \; =\; \partial \; H\; \partial \; pr\; =\; -\; (1\; -\; rsr)\; prd\; \phi \; d\; \tau \; =\; \partial \; H\; \partial \; p\; \phi \; =\; -\; p\; \phi \; r\; 2\; =\; acr\; 2\; dtd\; \tau \; =\; \partial \; H\; \partial \; pt\; =\; ptc\; 2\; (1\; -\; rsr)\; =\; ab\; (1\; -\; rsr)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; H\}\; \{\backslash \; partial\; p\_\; \{r\}\}\}\; =\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; p\_\; \{r\}\; \backslash \backslash \; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; H\}\; \{\backslash \; частичный\; p\; \_\; \{\backslash \; varphi\}\}\}\; =\; \{\backslash \; frac\; \{-p\; \_\; \{\backslash \; varphi\}\}\; \{r\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{ac\}\; \{r\; ^\; \{2\}\}\}\; \backslash \backslash \; \{\backslash \; frac\; \{dt\; \}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; H\}\; \{\backslash \; partial\; p\_\; \{t\}\}\}\; =\; \{\backslash \; frac\; \{p\_\; \{t\}\}\; \{c\; ^\; \{2\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\}\}\; =\; \{\backslash \; frac\; \{a\}\; \{b\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\})\; \backslash \; right)\}\}\; \backslash \; end\; \{align\}\}\}$

Дивидин g первое уравнение по второму дает уравнение орбиты

$drd\; \phi \; =\; -\; r\; 2\; ac\; (1\; -\; rsr)\; pr\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; =\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{ac\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; p\_\; \{r\}\}$

Радиальный импульс p r может быть выражено через r, используя постоянство гамильтониана $H\; =\; c\; 2\; 2\; \{\backslash \; textstyle\; H\; =\; \{\backslash \; frac\; \{c\; ^\; \{2\}\}\; \{2\}\}\}$; это дает фундаментальное уравнение орбиты

$(drd\; \phi )\; 2\; =\; r\; 4\; b\; 2\; -\; (1\; -\; rsr)\; (r\; 4\; a\; 2\; +\; r\; 2)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\; \}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{b\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\; \}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{a\; ^\; \{2\}\}\}\; +\; r\; ^\; \{2\}\; \backslash \; right)\}$

Подход Гамильтона – Якоби

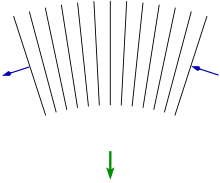
Изгиб волн в гравитационное поле. Из-за силы тяжести время внизу течет медленнее, чем вверху, в результате чего волновые фронты (показанные черным) постепенно изгибаются вниз. Зеленая стрелка показывает направление кажущегося «гравитационного притяжения».

Орбитальное уравнение может быть получено из уравнения Гамильтона – Якоби. Преимущество этого подхода состоит в том, что он приравнивает движение частицы к распространению волны и аккуратно приводит к выводу отклонения света под действием силы тяжести в общей теории относительности с помощью принципа Ферма.. Основная идея состоит в том, что из-за гравитационного замедления времени части волнового фронта, близкие к гравитирующей массе, движутся медленнее, чем те, что дальше, таким образом изменяя направление распространения волнового фронта.

Используя общую ковариацию, уравнение Гамильтона – Якоби для отдельной частицы единичной массы может быть выражено в произвольных координатах как

$g\; \mu \; \nu \; \partial \; S\; \partial \; x\; \mu \; \partial \; S\; \partial \; x\; \nu \; =\; с\; 2.\; \{\backslash \; displaystyle\; g\; ^\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; x\; ^\; \{\backslash \; mu\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; x\; ^\; \{\backslash \; nu\}\}\}\; =\; c\; ^\; \{2\}.\}$

Это эквивалентно гамильтоновой формулировке выше, в которой частные производные действия заменяют обобщенные импульсы. Используя метрику Шварцшильда g, это уравнение принимает вид

$1\; c\; 2\; (1\; -\; rsr)\; (\partial \; S\; \partial \; t)\; 2\; -\; (1\; -\; rsr)\; (\partial \; S\; \partial \; r)\; 2\; -\; 1\; r\; 2\; (\partial \; S\; \partial \; \phi )\; 2\; знак\; равно\; c\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{c\; ^\; \{2\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; t\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; справа)\; \backslash \; слева\; (\{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; r\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; c\; ^\; \{2\}\}$

где мы снова ориентируем сферическую систему координат относительно плоскости орбиты. Время t и азимутальный угол φ являются циклическими координатами, так что решение для главной функции Гамильтона S можно записать в виде

$S\; =\; -\; ptt\; +\; p\; \phi \; +\; S\; r\; (r)\; \{\backslash \; displaystyle\; S\; =\; -p\_\; \{t\}\; t\; +\; p\; \_\; \{\backslash \; varphi\}\; \backslash \; varphi\; +\; S\_\; \{r\}\; (r)\; \backslash ,\}$

где p t и p φ - постоянные обобщенные импульсы. Уравнение Гамильтона – Якоби дает интегральное решение для радиальной части S r (r)

$S\; r\; (r)\; =\; \int \; rdr\; 1\; -\; rsrpt\; 2\; c\; 2\; -\; (1\; -\; rsr)\; (c\; 2\; +\; p\; \phi \; 2\; r\; 2).\; \{\backslash \; displaystyle\; S\_\; \{r\}\; (r)\; =\; \backslash \; int\; ^\; \{r\}\; \{\backslash \; frac\; \{dr\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \{\backslash \; sqrt\; \{\{\; \backslash \; frac\; \{p\_\; \{t\}\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; right)\}\}.\}$

Взяв производную главной функции Гамильтона S по сохраняющейся импульс p φ дает

$\partial \; S\; \partial \; p\; \phi \; =\; \phi \; +\; \partial \; S\; r\; \partial \; p\; \phi \; =\; константа\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; p\; \_\; \{\backslash \; varphi\}\}\}\; =\; \backslash \; varphi\; +\; \{\backslash \; frac\; \{\backslash \; partial\; S\_\; \{r\}\}\; \{\backslash \; partial\; p\; \_\; \{\backslash \; varphi\}\}\}\; =\; \backslash \; mathrm\; \{constant\}\}$

что равняется

$\phi \; -\; \int \; rp\; \phi \; drr\; 2\; pt\; 2\; c\; 2\; -\; (1\; -\; rsr)\; (с\; 2\; +\; п\; \phi \; 2\; р\; 2)\; =\; константа\; \{\backslash \; displaystyle\; \backslash \; varphi\; -\; \backslash \; int\; ^\; \{r\}\; \{\backslash \; frac\; \{p\; \_\; \{\backslash \; varphi\}\; dr\}\; \{r\; ^\; \{2\}\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{p\_\; \{t\}\; ^\; \{2\}\}\; \{c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\; \_\; \{\backslash \; varphi\}\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; \backslash \; right)\}\}\}\}\; =\; \backslash \; mathrm\; \{constant\}\}$

Взяв бесконечно малую изменение φ и r дает фундаментальное уравнение орбиты

$(drd\; \phi )\; 2\; =\; r\; 4\; b\; 2\; -\; (1\; -\; rsr)\; (r\; 4\; a\; 2\; +\; r\; 2).\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{b\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1-\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{a\; ^\; \{2\}\}\}\; +\; r\; ^\; \{2\}\; \backslash \; right).\}$

где сохраняющиеся масштабы длины a и b определяются сохраняющимися импульсами уравнениями

$\partial \; S\; \partial \; \phi \; =\; p\; \phi \; =\; -\; ac\; \partial \; S\; \partial \; t\; =\; pt\; =\; ac\; 2\; b\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; \backslash \; varphi\}\}\; =\; p\; \_\; \{\backslash \; varphi\}\; =\; -\; ac\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; partial\; S\}\; \{\backslash \; partial\; t\}\}\; =\; p\_\; \{t\; \}\; =\; \{\backslash \; frac\; \{ac\; ^\; \{2\}\}\; \{b\}\}\; \backslash \; end\; \{align\}\}\}$

Принцип Гамильтона

Интеграл действия для частицы, на которую влияет только гравитация

$S\; =\; \int \; -\; mc\; 2\; d\; \tau \; =\; -\; mc\; \int \; cd\; \tau \; dqdq\; =\; -\; mc\; \int \; -\; g\; \mu \; \nu \; dx\; \mu \; dqdx\; \nu \; dqdq\; \{\backslash \; displaystyle\; S\; =\; \backslash \; int\; \{-mc\; ^\; \{2\}\; d\; \backslash \; tau\; \}\; =\; -\; mc\; \backslash \; int\; \{c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; dq\}\; =\; -\; mc\; \backslash \; int\; \{\{\backslash \; sqrt\; \{-g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\; \}\; \{dq\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; nu\}\}\; \{dq\}\}\}\}\; dq\}\}$

где $\tau \; \{\backslash \; textstyle\; \backslash \; tau\}$- это собственное время и $q\; \{\backslash \; textstyle\; q\}$- любая плавная параметризация мира частицы lin е. Если применить к этому вариационное исчисление, мы снова получим уравнения для геодезической. Чтобы упростить вычисления, сначала берется изменение квадрата подынтегрального выражения. Для метрики и координат этого случая и предполагая, что частица движется в экваториальной плоскости $\theta \; =\; \pi \; 2\; \{\backslash \; textstyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$, этот квадрат равен

$(cd\; \tau \; dq)\; 2\; =\; -\; g\; \mu \; \nu \; dx\; \mu \; dqdx\; \nu \; dq\; =\; (1\; -\; rsr)\; c\; 2\; (dtdq)\; 2\; -\; 1\; 1\; -\; rsr\; (drdq)\; 2\; -\; r\; 2\; (d\; \phi \; dq)\; 2.\; \{\backslash \; displaystyle\; \backslash \; left\; (c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; -\; g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; mu\}\}\; \{dq\}\}\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; nu\}\}\; \{dq\}\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \backslash \; left\; (\{\; \backslash \; frac\; \{dt\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash ,.\}$

Вариация этого значения дает

$\delta \; (cd\; \tau \; dq)\; 2\; =\; 2\; c\; 2\; d\; \tau \; dq\; \delta \; d\; \tau \; dq\; =\; \delta \; [(1\; -\; rsr)\; c\; 2\; (dtdq)\; 2\; -\; 1\; 1\; -\; rsr\; (drdq)\; 2\; -\; r\; 2\; (d\; \phi \; dq)\; 2].\; \{\backslash \; displaystyle\; \backslash \; delta\; \backslash \; left\; (c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; =\; 2c\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; =\; \backslash \; delta\; \backslash \; left\; [\backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \backslash \; left\; (\{\; \backslash \; frac\; \{dt\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; -r\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{dq\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; \backslash ,.\}$

Движение по долготе

Варьируйте по долготе $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$только для получения

$2\; c\; 2\; d\; \tau \; dq\; \delta \; d\; \tau \; dq\; =\; -\; 2\; r\; 2\; d\; \phi \; dq\; \delta \; d\; \phi \; dq.\; \{\backslash \; displaystyle\; 2c\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; =\; -\; 2r\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{\; dq\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{dq\}\}\; \backslash ,.\}$

Разделить на $2\; кд\; \tau \; dq\; \{\backslash \; textstyle\; 2c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\}$для получения вариации самого подынтегрального выражения

$c\; \delta \; d\; \tau \; dq\; =\; -\; r\; 2\; cd\; \phi \; d\; \tau \; \delta \; d\; \phi \; dq\; =\; -\; r\; 2\; cd\; \phi \; d\; \tau \; d\; \delta \; \phi \; dq.\; \{\backslash \; displaystyle\; c\; \backslash ,\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; =\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{dq\}\}\; =\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{d\; \backslash \; delta\; \backslash \; varphi\}\; \{dq\}\}\; \backslash ,.\}$

Таким образом,

$0\; =\; \delta \; \int \; cd\; \tau \; dqdq\; =\; c\; \delta \; d\; \tau \; dqdq\; =\; \int \; -\; r\; 2\; cd\; \phi \; d\; \tau \; d\; \delta \; \phi \; dqdq.\; \{\backslash \; displaystyle\; 0\; =\; \backslash \; delta\; \backslash \; int\; \{c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; dq\}\; =\; \backslash \; int\; \{c\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; dq\}\; =\; \backslash \; int\; \{\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{d\; \backslash \; delta\; \backslash \; varphi\}\; \{dq\}\}\; dq\}\; \backslash ,.\}$

Интегрированиепо частям дает

$0\; =\; -\; r\; 2\; cd\; \phi \; d\; \tau \; \delta \; \phi \; -\; ddq\; [-\; r\; 2\; cd\; \phi \; d\; \tau ]\; \delta \; \phi \; dq.\; \{\backslash \; displaystyle\; 0\; =\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; delta\; \backslash \; varphi\; -\; \backslash \; int\; \{\{\backslash \; frac\; \{d\}\; \{dq\; \}\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right]\; \backslash \; delta\; \backslash \; varphi\; dq\}\; \backslash ,.\}$

Предполагается, что изменение долготы в конечных точках равно нулю, поэтому первый член исчезает. Интеграл может быть ненулевым путем неправильного выбора $\delta \; \phi \; \{\backslash \; textstyle\; \backslash \; delta\; \backslash \; varphi\}$, если другой множитель внутри не равен нулю всюду. Таким образом, уравнение движения:

$d\; d\; q\; [-\; r\; 2\; c\; d\; \phi \; d\; \tau ]\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dq\}\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{c\}\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right]\; =\; 0\; \backslash ,.\}$

Движение во времени

Изменяйте во времени $t\; \{\backslash \; textstyle\; t\}$только для получения

$2\; c\; 2\; d\; \tau \; dq\; \delta \; d\; \tau \; dq\; =\; 2\; (1\; -\; rsr)\; c\; 2\; dtdq\; \delta \; dtdq.\; \{\backslash \; displaystyle\; 2c\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; =\; 2\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{\; s\}\}\}\; \{r\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; \{\backslash \; frac\; \{dt\}\; \{dq\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{dt\}\; \{dq\}\}\; \backslash ,.\}$

Разделить на $2\; cd\; \tau \; dq\; \{\backslash \; textstyle\; 2c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\}$, чтобы получить вариацию самого подынтегрального выражения

$c\; \delta \; d\; \tau \; dq\; =\; c\; (1\; -\; rsr)\; dtd\; \tau \; \delta \; dtdq\; =\; c\; (1\; -\; rsr)\; dtd\; \tau \; d\; \delta \; tdq.\; \{\backslash \; displaystyle\; c\; \backslash \; delta\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; =\; c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\; \}\; \{d\; \backslash \; tau\}\}\; \backslash \; delta\; \{\backslash \; frac\; \{dt\}\; \{dq\}\}\; =\; c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{\; dt\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{d\; \backslash \; delta\; t\}\; \{dq\}\}\; \backslash ,.\}$

Таким образом,

$0\; =\; \delta \; \int \; cd\; \tau \; dqdq\; =\; \int \; c\; (1\; -\; rsr)\; dtd\; \tau \; d\; \delta \; tdqdq.\; \{\backslash \; displaystyle\; 0\; =\; \backslash \; delta\; \backslash \; int\; \{c\; \{\backslash \; frac\; \{d\; \backslash \; tau\}\; \{dq\}\}\; dq\}\; =\; \backslash \; int\; \{c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\; \}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \{\backslash \; frac\; \{d\; \backslash \; delta\; t\}\; \{dq\}\}\; dq\}\; \backslash ,.\}$

Интегрирование по частям дает

$0\; =\; c\; (\; 1\; -\; rsr)\; dtd\; \tau \; \delta \; t\; -\; \int \; ddq\; [c\; (1\; -\; rsr)\; dtd\; \tau ]\; \delta \; tdq.\; \{\backslash \; displaystyle\; 0\; =\; c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \backslash \; delta\; t-\; \backslash \; int\; \{\; \{\backslash \; frac\; \{d\}\; \{dq\}\}\; \backslash \; left\; [c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\; \}\; \backslash \; right]\; \backslash \; delta\; tdq\}\; \backslash ,.\}$

Итак, уравнение движения:

$ddq\; [c\; (1\; -\; rsr)\; dtd\; \tau ]\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dq\}\}\; \backslash \; left\; [c\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right]\; =\; 0\; \backslash ,.\}$

Сохраняющиеся импульсы

Проинтегрируйте эти уравнения движения, чтобы определить константы интегрирования, получив

$L\; =\; p\; \varphi \; =\; mr\; 2\; d\; \phi \; d\; \tau ,\; E\; =\; -\; pt\; =\; mc\; 2\; (1\; -\; rsr)\; dtd\; \tau .\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; L\; =\; p\; \_\; \{\backslash \; phi\}\; =\; mr\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash ,,\; \backslash \backslash \; E\; =\; -p\_\; \{t\}\; =\; mc\; ^\; \{2\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; \backslash ,.\; \backslash \; end\; \{выровнено\; \}\}\}$

Эти два уравнения для констант движения $L\; \{\backslash \; textstyle\; L\}$(угловой момент) и $E\; \{\backslash \; textstyle\; E\}$( энергия) можно объединить, чтобы сформировать одно уравнение, которое справедливо даже для фотонов и других безмассовых частиц, для которых собственное время вдоль геодезической равно нулю.

$d\; \phi \; d\; t\; =\; (1\; -\; r\; s\; r)\; L\; c\; 2\; E\; r\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{dt\}\}\; =\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{L\; \backslash ,\; c\; ^\; \{2\}\}\; \{E\; \backslash ,\; r\; ^\; \{2\}\}\}\; \backslash ,.\}$

Радиальное движение

Подставив

$d\; \phi \; d\; \tau \; =\; L\; mr\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{L\}\; \{m\; \backslash ,\; r\; ^\; \{2\}\}\}\; \backslash ,\}$

и

$dtd\; \tau \; =\; E\; (1\; -\; rsr)\; mc\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; tau\}\}\; =\; \{\backslash \; frac\; \{E\}\; \{\backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; m\; \backslash ,\; c\; ^\; \{2\}\}\}\; \backslash ,\}$

в метрическое уравнение (и используя $\theta \; =\; \pi \; 2\; \{\backslash \; textstyle\; \backslash \; theta\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\}$) дает

$c\; 2\; =\; 1\; 1\; -\; rsr\; E\; 2\; m\; 2\; c\; 2\; -\; 1\; 1\; -\; rsr\; (drd\; \tau )\; 2\; -\; 1\; r\; 2\; L\; 2\; m\; 2,\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{\; 1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash ,\; \{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{r\; ^\; \{2\}\}\}\; \backslash ,\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\}\}\; \backslash ,,\}$

из которого можно получить

$(ДРД\; \tau )\; 2\; знак\; равно\; Е\; 2\; м\; 2\; с\; 2\; -\; (1\; -\; RSR)\; (с\; 2\; +\; L\; 2\; м\; 2\; р\; 2),\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; tau\}\}\; \backslash \; справа)\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{E\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (c\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; r\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash ,,\}$

, которое является уравнением движения для $r\; \{\backslash \; textstyle\; r\}$. Зависимость $r\; \{\backslash \; textstyle\; r\}$от $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$можно найти, разделив это на

$(d\; \phi \; d\; \tau )\; 2\; =\; L\; 2\; м\; 2\; р\; 4\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{d\; \backslash \; varphi\}\; \{d\; \backslash \; tau\}\}\; \backslash \; right)\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{L\; ^\; \{2\}\}\; \{\; m\; ^\; \{2\}\; r\; ^\; \{4\}\}\}\}$

, чтобы получить

$(drd\; \phi )\; 2\; =\; E\; 2\; r\; 4\; L\; 2\; c\; 2\; -\; (1\; -\; rsr)\; (m\; 2\; c\; 2\; r\; 4\; L\; 2\; +\; р\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{E\; ^\; \{2\}\; r\; ^\; \{4\}\}\; \{L\; ^\; \{2\}\; c\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{m\; ^\; \{2\}\; c\; ^\; \{2\}\; r\; ^\; \{4\}\}\; \{L\; ^\; \{2\}\}\}\; +\; r\; ^\; \{2\}\; \backslash \; right)\; \backslash ,\}$

что верно даже для частиц без массы. Если масштабы длины определены как

$a\; =\; L\; mc\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; frac\; \{L\}\; \{m\; \backslash ,\; c\}\}\}$

и

$b\; =\; L\; c\; E,\; \{\backslash \; displaystyle\; b\; =\; \{\backslash \; frac\; \{L\; \backslash ,\; c\}\; \{E\}\}\; \backslash ,,\}$

, тогда зависимость $r\; \{\backslash \; textstyle\; r\}$от $\phi \; \{\backslash \; textstyle\; \backslash \; varphi\}$упрощается до

$(drd\; \phi )\; 2\; =\; r\; 4\; b\; 2\; -\; (1\; -\; rsr)\; (r\; 4\; a\; 2\; +\; r\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; left\; (\{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; varphi\}\}\; \backslash \; right)\}\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{b\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (\; 1\; -\; \{\backslash \; frac\; \{r\; \_\; \{\backslash \; rm\; \{s\}\}\}\; \{r\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{r\; ^\; \{4\}\}\; \{a\; ^\; \{2\}\}\}\; +\; r\; ^\; \{2\}\; \backslash \; справа)\; \backslash ,.\}$

• Проблема Кеплера
• Классическая проблема центральной силы
• Задача двух тел в общей теории относительности
• Фреймовые поля в общей теории относительности

1. ^Это замена r на u также обычна в классических задачах с центральной силой, поскольку она также упрощает решение этих уравнений. Для получения дополнительной информации см. Статью о классической задаче центральной силы.
2. ^В математической литературе K известен как полный эллиптический интеграл первого рода ; для получения дополнительной информации см. статью о эллиптических интегралах.

1. ^Ландау и Лифшиц, стр. 299–301.
2. ^Whittaker 1937.
3. ^Ландау и Лифшиц (1975), стр. 306–309.
4. ^Гиббонс и Виска, «Применение эллиптических функций Вейерштрасса к нулевой геодезии Шварцшильда», https://arxiv.org/abs/1110.6508
5. ^Synge, стр. 294–295.
6. ^arXiv.org: gr-qc / 9907034v1.
7. ^Шон Кэрролл : Конспект лекций по общей теории относительности, глава 7, уравнение. 7.33
8. ^Вайнберг, стр. 122.
9. ^Эйнштейн, стр. 95–96.
10. ^Вайнберг, стр. 185–188; Wald, стр. 138–139.
11. ^Synge, стр. 290–292; Адлер, Базин и Шиффер, стр. 179–182; Whittaker, стр. 390–393; Паули, стр. 167.
12. ^Ланцош, стр. 331–338.
13. ^Ландау, Лифшиц, стр. 306–307; Миснер, Торн и Уиллер, стр. 636–679.

• Шварцшильд, К. (1916). Über das Gravitationsfeld eines Massenpunktes nach der Einstein'schen Theorie. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1, 189–196.
  • сканирование оригинальной статьи
  • текст оригинальной статьи, в Wikisource
  • перевод Antoci и Loinger
  • комментарий к статье, дающий более простой вывод
• Schwarzschild, K. (1916). Über das Gravitationsfeld einer Kugel aus inkompressibler Flüssigkeit. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 1, 424- ?.
• Flamm, L (1916). "Beiträge zur Einstein'schen Gravitationstheorie". Physikalische Zeitschrift. 17 : 448– ?.
• Адлер, Р; Базин М; Шиффер М (1965). Введение в общую теорию относительности. Нью-Йорк: Книжная компания Макгроу-Хилл. Стр. 177 –193. ISBN 978-0-07-000420-7.
• Эйнштейн, A (1956). Значение относительности (5-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. Стр. 92 –97. ISBN 978-0-691-02352-6.
• Хагихара, Y (1931). «Теория релятивистских траекторий в гравитационном поле Шварцшильда». Японский журнал астрономии и геофизики. 8 : 67–176. ISSN 0368-346X.
• Lanczos, C. (1986). Вариационные принципы механики (4-е изд.). Нью-Йорк: Dover Publications. С. 330–338. ISBN 978-0-486-65067-8.
• Ландау, LD ; Лифшиц, Э.М. (1975). Классическая теория поля. Курс теоретической физики. Vol. 2 (переработанное 4-е английское изд.). Нью-Йорк: Pergamon Press. С. 299–309. ISBN 978-0-08-018176-9.
• Миснер, телеканал ; Торн, К. и Уиллер, Дж. А. (1973). Гравитация. Сан-Франциско: В. Х. Фриман. стр. Глава 25 (стр. 636–687), §33.5 (стр. 897–901) и §40.5 (стр. 1110–1116). ISBN 978-0-7167-0344-0.(см. Gravitation (книга).)
• Pais, A. (1982). Тонкое - это Господь: Наука и жизнь Альберта Эйнштейна. Oxford University Press. стр. 253–256. ISBN 0-19-520438-7.
• Pauli, W (1958). Theory of Relativity. Translated by G. Field. New York: Dover Publications. Pp. 40 –41, 166–169. ISBN 978-0-486-64152-2.
• Риндлер, W (1977). Существенная теория относительности: специальная, общая и космологическая (пересмотренное 2-е изд. Нью-Йорк: Springer Verlag. Pp. 143 –149. ISBN 978-0-387-10090-6.
• Roseveare, N.T (1982 Перигелий Меркурия, от Леверье до Эйнштейна. Oxford: University Press. ISBN 0-19-858174-2.

• Synge, JL (1960). Относительность: Общая теория. Амстердам: North-Holland Publishing. Стр. 289 –298. ISBN 978-0-7204-0066- 3.
• Wald, RM (1984). Общая теория относительности. Chic назад: Издательство Чикагского университета. Стр. 136 –146. ISBN 978-0-226-87032-8.
• Уолтер, С. (2007). «Разбивка на 4-вектора: четырехмерное движение в гравитации, 1905–1910». В Ренн, Дж. (Ред.). Генезис общей теории относительности. 3 . Берлин: Springer. pp. 193–252.

• Weinberg, S (1972). Gravitation and Cosmology. Нью-Йорк: Джон Уайли и сыновья. pp. 185–201. ISBN 978-0-471-92567-5.
• Whittaker, ET (1937). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies (4th ed.). Нью-Йорк: Dover Publications. pp. 389 –393. ISBN 978-1-114-28944-4.

• Excerpt from Reflections on Relativity by Kevin Brown.