Прыгающий мяч

редактировать

Физика прыгающего мяча

Прыгающий мяч. Движение не совсем параболическое из-за сопротивления воздуха.

Физика прыгающего мяча касается физического поведения подпрыгивающего мяча., особенно его движение до, во время и после удара о поверхность другого тела. Некоторые аспекты поведения прыгающего мяча служат введением в механику на курсах физики старшей школы или бакалавриата. Однако точное моделирование поведения является сложным и представляет интерес в спортивной инженерии.

Движение мяча обычно описывается движением снаряда (на которое может влиять гравитация, сопротивление, эффект Магнуса и плавучесть ), в то время как его влияние обычно характеризуется через коэффициент восстановления (который может зависеть от природы мяча, характера ударной поверхности, скорости удара, вращения и местных условий, таких как температура и давление ). Чтобы обеспечить честную игру, многие спортивные руководящие органы устанавливают ограничения на подпрыгивание своего мяча и запрещают изменение аэродинамических свойств мяча. Подпрыгивание мячей было особенностью таких древних видов спорта, как мезоамериканская игра с мячом.

Содержание

1 Силы во время полета и влияние на движение
- 1.1 Гравитация
- 1.2 Сопротивление
- 1.3 Эффект Магнуса
- 1.4 Плавучесть
2 Удар
- 2.1 Вращение и угол удара
- 2.2 Несферические мячи
- 2.3 Несколько уложенных друг на друга мячей
3 Спортивные правила
4 См. Также
5 Примечания
6 Ссылки
7 Дополнительная литература

Силы во время полета и влияние на движение

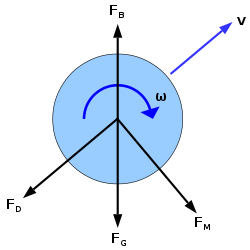Силами, действующими на вращающийся шар во время полета, являются сила тяжести (FG), сила сопротивления (FD), сила Магнуса (FM) и выталкивающая сила (FB).

. Движение прыгающего мяча подчиняется движению снаряда. На настоящий шар действует множество сил, а именно сила тяжести (FG), сила сопротивления, обусловленная сопротивлением воздуха (FD), сила Магнуса из-за вращения (FMмяча) и выталкивающей силы (FB). В общем, для анализа движения мяча необходимо использовать второй закон Ньютона с учетом всех сил:

∑ F = ma, FG + FD + FM + FB = ma = mdvdt = md 2 rdt 2, {\ displaystyle {\ begin {align} \ sum \ mathbf {F} = m \ mathbf {a}, \\\ mathbf {F} _ {\ text {G}} + \ mathbf {F} _ { \ text {D}} + \ mathbf {F} _ {\ text {M}} + \ mathbf {F} _ {\ text {B}} = m \ mathbf {a} = m {\ frac {d \ mathbf {v}} {dt}} = m {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2}}}, \ end {align}}}

{\ displaystyle {\ begin {align} \ sum \ mathbf {F} = m \ mathbf {a}, \\\ mathbf {F} _ {\ text {G}} + \ mathbf {F} _ {\ text {D}} + \ mathbf {F} _ {\ text {M} } + \ mathbf {F} _ {\ text {B}} = m \ mathbf {a} = m {\ frac {d \ mathbf {v}} {dt}} = m {\ frac {d ^ {2 } \ mathbf {r}} {dt ^ {2}}}, \ end {align}}}

где m - значение мяча масса. Здесь a, v, rпредставляют собой ускорение, скорость и положение шара за время t.

Гравитация

Траектория отскока мяча под углом 70 ° после удара без сопротивления, с сопротивлением Стокса и с Сопротивление Ньютона.

Сила тяжести направлена вниз и равна

FG = mg, {\ displaystyle F _ {\ text {G}} = mg,}

{\ displaystyle F _ {\ text {G}} = mg,}

где m - масса шара, и g - ускорение свободного падения, которое на Земле изменяется от 9,764 м / с до 9,834 м / с. Поскольку другие силы обычно малы, движение часто идеализируется как происходящее только под действием силы тяжести. Если на мяч действует только сила тяжести, механическая энергия будет сохранена во время полета. В этом идеализированном случае уравнения движения задаются следующим образом:

a = - gj ^, v = v 0 + at, r = r 0 + v 0 t + 1 2 at 2, {\ displaystyle {\ begin {align } \ mathbf {a} = - g \ mathbf {\ hat {j}}, \\\ mathbf {v} = \ mathbf {v} _ {\ text {0}} + \ mathbf {a} t, \\\ mathbf {r} = \ mathbf {r} _ {0} + \ mathbf {v} _ {0} t + {\ frac {1} {2}} \ mathbf {a} t ^ {2}, \ end {align}}}

{\ displaystyle {\ begin {align} \ mathbf { a} = - g \ mathbf {\ hat {j}}, \\\ mathbf {v} = \ mathbf {v} _ {\ text {0}} + \ mathbf {a} t, \\\ mathbf {r} = \ mathbf {r} _ {0} + \ mathbf {v} _ {0} t + {\ frac {1} {2}} \ mathbf {a} t ^ {2}, \ end {выровнено }}}

где a, vи r обозначают ускорение, скорость и положение мяча, а v0и r0- начальная скорость и положение мяч соответственно.

Более конкретно, если мяч отскакивает под углом θ от земли, движение по осям x и y (представляющее горизонтальное и вертикальное движение соответственно) описывается осью

x: $ax = 0, vx = v 0 cos ⁡ (θ), x = x 0 + v 0 cos ⁡ (θ) t, {\ displaystyle {\ begin {align} a _ {\ text {x}} = 0, \\ v _ {\ text {x}} = v_ {0} \ cos \ left (\ theta \ right), \\ x = x_ {0} + v_ {0} \ cos \ left (\ theta \ справа) t, \ end {align}}}$ ${\ displaystyle {\ begin {align} a_ {\ text {x}} = 0, \\ v _ {\ text {x}} = v_ {0} \ cos \ left (\ theta \ right), \\ x = x_ {0} + v_ {0 } \ соз \ влево (\ тета \ вправо) т, \ конец {выровнено}}}$

ось y: $ay = - g, vy = v 0 sin ⁡ (θ) - gt, y = y 0 + v 0 sin ⁡ (θ) t - 1 2 гт 2. {\ displaystyle {\ begin {align} a _ {\ text {y}} = - g, \\ v _ {\ text {y}} = v_ {0} \ sin \ left (\ theta \ right) -gt, \\ y = y_ {0} + v_ {0} \ sin \ left (\ theta \ right) t - {\ frac {1} {2}} gt ^ {2}. \ end {align}}}$ ${\ displaystyle {\ begin {align} a _ {\ text {y}} = - g, \\ v _ {\ text {y}} = v_ {0} \ sin \ left (\ theta \ right) -gt, \\ y = y_ {0} + v_ {0} \ sin \ left (\ theta \ right) t - {\ frac {1} {2}} gt ^ {2}. \ end {align}}}$

Уравнения подразумевают, что максимальная высота (H) и диапазон (R) и время полета (T) мяча, отскакивающего от плоской поверхности, задаются как

H = v 0 2 2 g sin 2 ⁡ (θ), R = v 0 2 g sin ⁡ (2 θ) и T = 2 v 0 g sin ⁡ (θ). {\ displaystyle {\ begin {align} H = {\ frac {v_ {0} ^ {2}} {2g}} \ sin ^ {2} \ left (\ theta \ right), \\ R = {\ frac {v_ {0} ^ {2}} {g}} \ sin \ left (2 \ theta \ right), ~ {\ text {and}} \\ T = {\ frac {2v_ {0}} {g} } \ sin \ left (\ theta \ right). \ end {align}}}

{ \ Displaystyle {\ begin {align} H = {\ frac {v_ {0} ^ {2}} {2g}} \ sin ^ {2} \ left (\ theta \ right), \\ R = {\ frac { v_ {0} ^ {2}} {g}} \ sin \ left (2 \ theta \ right), ~ {\ text {and}} \\ T = {\ frac {2v_ {0}} {g}} \ грех \ влево (\ тета \ вправо). \ конец {выровнено}}}

Дальнейшие уточнения движения мяча могут быть сделаны с учетом сопротивления воздуха (и связанные эффекты, такие как сопротивление и ветер ), эффект Магнуса и плавучесть. Поскольку более легкие шары ускоряются быстрее, на их движение, как правило, больше влияют такие силы.

Перетаскивание

Поток воздуха вокруг шара может быть ламинарным или турбулентным в зависимости от числа Рейнольдса (Re), определяется как:

Re = ρ D v μ, {\ displaystyle {\ text {Re}} = {\ frac {\ rho Dv} {\ mu}},}

{\ displaystyle {\ text {Re}} = {\ frac {\ rho Dv} {\ mu}},}

где ρ - плотность воздуха, μ динамическая вязкость воздуха, D диаметр шара и v скорость шара в воздухе. При температуре 20 ° C, ρ = 1,2 кг / м и μ = 1,8 · 10 Па · с.

Если число Рейнольдса очень низкое (Re <1), сила лобового сопротивления шара описывается законом Стокса :

FD = 6 π μ rv, {\ displaystyle F _ {\ text {D}} = 6 \ pi \ mu rv,}

{\ displaystyle F _ {\ text {D}} = 6 \ pi \ mu rv,}

где r - радиус шара. Эта сила действует против направления мяча (в направлении $- v ^ {\ displaystyle \ textstyle - {\ hat {\ mathbf {v}}}}$ ${\ displaystyle \ textstyle - {\ hat {\ mathbf {v}}}}$ ). Однако для большинства спортивных мячей число Рейнольдса составляет от 10 до 10, и закон Стокса не применяется. При этих более высоких значениях числа Рейнольдса сила сопротивления мяча вместо этого описывается уравнением сопротивления :

FD = 1 2 ρ C d A v 2, {\ displaystyle F _ {\ text {D}} = {\ frac {1} {2}} \ rho C _ {\ text {d}} Av ^ {2},}

{\ displaystyle F _ {\ text {D}} = {\ frac {1} {2}} \ rho C _ {\ текст {d}} Av ^ {2},}

где C d - коэффициент сопротивления, и A площадь поперечного сечения мяча.

Перетаскивание приведет к потере механической энергии мячом во время полета и уменьшит его дальность и высоту, в то время как боковой ветер отклонит его от первоначального пути. Оба эффекта должны быть приняты во внимание игроками, занимающимися такими видами спорта, как гольф.

Эффект Магнуса

Сила Магнуса, действующая на шар с обратным вращением. Фигурные линии тока представляют собой турбулентный след. Воздушный поток был отклонен в направлении вращения.

Обратное вращение для настольного тенниса

В настольном теннисе опытный игрок может использовать вращение мяча, чтобы повлиять на траекторию мяча во время его полета и его реакция при ударе о поверхность. При использовании topspin мяч достигает максимальной высоты в процессе полета (1), а затем резко изгибается вниз (2). Удар толкает мяч вперед (3) и будет стремиться отскочить вверх при ударе по ракетке противоположного игрока. В случае обратного вращения.

ситуация обратная. Вращение мяча повлияет на его траекторию посредством эффекта Магнуса. Согласно теореме Кутты – Жуковского, для вращающейся сферы с невязким потоком воздуха сила Магнуса равна

FM = 8 3 π r 3 ρ ω v, {\ displaystyle F _ {\ text {M}} = {\ frac {8} {3}} \ pi r ^ {3} \ rho \ omega v,}

{\ displaystyle F _ {\ text {M}} = {\ frac { 8} {3}} \ pi r ^ {3} \ rho \ omega v,}

где r - радиус шара, ω угловая скорость (или скорость вращения) мяча, ρ - плотность воздуха, а v - скорость мяча относительно воздуха. Эта сила направлена перпендикулярно движению и перпендикулярно оси вращения (в направлении $ω ^ × v ^ {\ displaystyle \ textstyle {\ hat {\ mathbf {\ omega}}} \ times {\ hat {\ mathbf {v}}}}$ ${\ displaystyle \ textstyle {\ hat {\ mathbf {\ omega}}} \ times {\ hat {\ mathbf {v}}}}$ ). Сила направлена вверх для обратного вращения и вниз для верхнего вращения. На самом деле поток никогда не бывает гладким, и подъемная сила Магнуса лучше описывается следующим образом:

FM = 1 2 ρ CLA v 2, {\ displaystyle F _ {\ text {M}} = {\ frac {1} {2}} \ rho C _ {\ text {L}} Av ^ {2},}

{\ displaystyle F _ {\ text {M}} = {\ frac {1} {2}} \ rho C _ {\ text {L}} Av ^ {2},}

где ρ - плотность воздуха, C L коэффициент подъемной силы, A - поперечный площадь сечения мяча и v скорость мяча относительно воздуха. Коэффициент подъемной силы является комплексным фактором, который зависит, среди прочего, от отношения rω / v, числа Рейнольдса и шероховатости поверхности. В определенных условиях коэффициент подъемной силы может быть даже отрицательным, изменяя направление силы Магнуса ().

В таких видах спорта, как теннис или волейбол, игрок может используйте эффект Магнуса для управления траекторией мяча (например, с помощью topspin или backspin ) во время полета. В гольфе эффект отвечает за разрезание и зацепление, которые обычно вредят гольфисту, но также помогают увеличить дальность драйва и других выстрелы. В бейсбол, питчеры используют эффект для создания кривых мячей и других специальных питчей.

Подделка мяча часто является незаконной и часто в центре крикета споров, таких как спор между Англией и Пакистаном в августе 2006 года. В бейсболе термин «плевательница » относится к незаконному покрытию мяча слюной или другими веществами для изменения аэродинамики мяча.

Плавучесть

Любой объект, погруженный в жидкость, например воду или воздух, будет испытывать подъемную плавучесть. Согласно принципу Архимеда, эта выталкивающая сила равна весу жидкости, вытесняемой объектом. В случае шара эта сила равна

F B = 4 3 π r 3 ρ g. {\ displaystyle F _ {\ text {B}} = {\ frac {4} {3}} \ pi r ^ {3} \ rho g.}

{\ displaystyle F _ {\ text {B}} = {\ frac {4} {3}} \ pi r ^ {3} \ rho g.}

Выталкивающая сила обычно мала по сравнению с силой сопротивления и силы Магнуса. и им часто можно пренебречь. Однако в случае с баскетбольным мячом подъемная сила может составлять около 1,5% веса мяча. Поскольку плавучесть направлена вверх, она увеличивает дальность полета и высоту мяча.

Удар

Сжатие (A → B) и декомпрессия (B → C) удара мяча о поверхность. Сила удара обычно пропорциональна расстоянию сжатия, по крайней мере, для небольших сжатий, и может быть смоделирована как сила пружины.

Внешнее видео
Флориан Корн (2013). «Мяч подпрыгивает в замедленной съемке: резиновый мяч». YouTube.

Когда мяч ударяется о поверхность, поверхность отскакивает и вибрирует, как и мяч, создавая звук и нагреваются, и мяч теряет кинетическую энергию. Кроме того, удар может придать шару некоторое вращение, передав часть его поступательной кинетической энергии в кинетической энергии вращения. Эти потери энергии обычно характеризуются (косвенно) через коэффициент восстановления (или COR, обозначаемый e):

e = - vf - ufvi - ui, {\ displaystyle e = - {\ frac { v _ {\ text {f}} - u _ {\ text {f}}} {v _ {\ text {i}} - u _ {\ text {i}}}},}

{\ displaystyle e = - {\ frac {v _ {\ text {f}} - u _ {\ text {f}}} {v _ {\ text {i}} - u _ {\ text {i}}}},}

где v f и v i - конечная и начальная скорости мяча, а u f и u i - конечная и начальная скорости удара о поверхность соответственно. В конкретном случае, когда мяч ударяется о неподвижную поверхность, COR упрощается до

e = - v f v i. {\ displaystyle e = - {\ frac {v _ {\ text {f}}} {v _ {\ text {i}}}}.}

{\ displaystyle e = - {\ frac {v _ {\ text {f}}} {v _ {\ text {i }}}}.}

Таким образом, для мяча, упавшего на пол, COR будет варьироваться от 0 (без отскока, полная потеря энергии) и 1 (идеально подскакивает, без потери энергии). Значение COR ниже 0 или выше 1 теоретически возможно, но будет означать, что мяч прошел через поверхность (e < 0), or that the surface was not "relaxed" when the ball impacted it (e>1), как в случае приземления мяча на подпружиненную платформу.

Для анализа вертикальной и горизонтальной составляющих движения COR иногда разделяется на нормальный COR (e y) и тангенциальный COR (e x), определяемый как

ey = - v yf - u yf v yi - u yi, {\ displaystyle e _ {\ text {y}} = - {\ frac { v _ {\ text {yf}} - u _ {\ text {yf}}} {v _ {\ text {yi}} - u _ {\ text {yi}}}},}

{\ displaystyle e _ {\ text {y}} = - {\ frac {v _ {\ text {yf}} - u _ {\ text {yf}}} {v_ { \ text {yi}} - u _ {\ text {yi}}}},}

ex = - (v xf - р ω е) - (U XF - R Ω е) (v XI - р ω я) - (U XI - R Ω я), {\ Displaystyle е _ {\ текст {х}} = - {\ гидроразрыва {(v_ {\ text {xf}} - r \ omega _ {\ text {f}}) - (u _ {\ text {xf}} - R \ Omega _ {\ text {f}})} {(v _ {\ text {xi}} - r \ omega _ {\ text {i}}) - (u _ {\ text {xi}} - R \ Omega _ {\ text {i}})}},}

{\ displaystyle e _ {\ text {x}} = - {\ frac {(v _ {\ text {xf}) } -r \ omega _ {\ text {f}}) - (u _ {\ text {xf}} - R \ Omega _ {\ text {f}})} {(v _ {\ text {xi}} - r \ omega _ {\ text {i}}) - (u _ {\ text {xi}} - R \ Omega _ {\ text {i}})}},}

где r и ω обозначают радиус и угловую скорость мяча, а R и Ω обозначают радиус и угловую скорость ударной поверхности (такой как бейсбольная бита). В частности, rω - это тангенциальная скорость поверхности шара, а RΩ - тангенциальная скорость ударной поверхности. Это особенно интересно, когда мяч ударяется о поверхность под углом наклона или когда задействовано вращение.

Для прямого падения на землю без вращения, когда на мяч действует только сила тяжести, COR можно связать с несколькими другими величинами следующим образом:

e = | v f v i | = К е К я = U е U я = Н е Н я = Т е Т я = г Т е 2 8 H я. {\ displaystyle e = \ left | {\ frac {v _ {\ text {f}}} {v _ {\ text {i}}}} \ right | = {\ sqrt {\ frac {K _ {\ text {f} }} {K _ {\ text {i}}}}} = {\ sqrt {\ frac {U _ {\ text {f}}} {U _ {\ text {i}}}}} = {\ sqrt {\ frac {H _ {\ text {f}}} {H _ {\ text {i}}}}} = {\ frac {T _ {\ text {f}}} {T _ {\ text {i}}}} = {\ sqrt {\ frac {gT _ {\ text {f}} ^ {2}} {8H _ {\ text {i}}}}}.}

{\ displaystyle e = \ left | {\ frac {v _ {\ text {f}}} {v_ { \ text {i}}}} \ right | = {\ sqrt {\ frac {K _ {\ text {f}}} {K _ {\ text {i}}}}} = {\ sqrt {\ frac {U_ { \ text {f}}} {U _ {\ text {i}}}}} = {\ sqrt {\ frac {H _ {\ text {f}}} {H _ {\ text {i}}}}} = { \ frac {T _ {\ text {f}}} {T _ {\ text {i}}}} = {\ sqrt {\ frac {gT _ {\ text {f}} ^ {2}} {8H _ {\ text {i}}}}}.}

Здесь K и U обозначают кинетический и потенциальная энергия мяча, H - максимальная высота мяча, а T - время полета мяча. Индексы «i» и «f» относятся к начальному (до удара) и конечному (после удара) состояниям мяча. Аналогичным образом, потеря энергии при ударе может быть связана с COR следующим образом:

Потери энергии = K i - K f K i × 100% = (1 - e 2) × 100%. {\ displaystyle {\ text {Energy Loss}} = {\ frac {{K _ {\ text {i}}} - {K _ {\ text {f}}}} {K _ {\ text {i}}}} \ times 100 \% = \ left (1-e ^ {2} \ right) \ times 100 \%.}

{\ displaystyle {\ text {Energy Loss}} = {\ frac {{K _ {\ text {i}}} - {K _ {\ text {f}}}} {K _ {\ text {i}}} } \ times 100 \% = \ left (1-e ^ {2} \ right) \ times 100 \%.}

COR шара может зависеть от нескольких факторов, в основном

природы ударной поверхности (например, трава, бетон, проволочная сетка)
материал мяча (например, кожа, резина, пластик)
давление внутри мяча (если он полый)
величина вращения, вызываемая в шаре при ударе
скорость удара

Внешние условия, такие как температура, могут изменить свойства ударной поверхности или шара, делая их более гибкими или более жесткий. Это, в свою очередь, повлияет на COR. В общем, мяч будет деформироваться больше при более высоких скоростях удара и, соответственно, потеряет больше своей энергии, уменьшая свой COR.

Вращение и угол удара

Силы, действующие на вращающийся шар во время удара, являются сила тяжести, нормальная сила и сила трения (которая обычно имеет как «поступательную», так и «вращательную» составляющую). Если поверхность наклонена под углом, сила тяжести будет находиться под углом к поверхности, в то время как другие силы останутся перпендикулярными или параллельными поверхности.

Внешнее видео
BiomechanicsMMU (2008). «Удары гольфа - замедленное видео». YouTube.

При ударе о землю часть поступательной кинетической энергии может быть преобразована в кинетическую энергию вращения и наоборот, в зависимости от угла удара и угловой скорости мяча. Если при ударе мяч движется горизонтально, трение будет иметь «поступательный» компонент в направлении, противоположном движению мяча. На рисунке мяч движется вправо, и поэтому он будет иметь поступательную составляющую трения, толкающую мяч влево. Кроме того, если мяч вращается при ударе, трение будет иметь «вращательную» составляющую в направлении, противоположном вращению мяча. На рисунке мяч вращается по часовой стрелке, а точка, касающаяся земли, перемещается влево относительно центра масс мяча. Таким образом, вращательная составляющая трения толкает мяч вправо. В отличие от нормальной силы и силы тяжести, эти силы трения будут оказывать на мяч крутящий момент и изменять его угловую скорость (ω).

Могут возникнуть три ситуации:

Если мяч продвигается вперед с обратным вращением, поступательное и вращательное трение будут действовать в одних и тех же направлениях. Угловая скорость мяча будет уменьшена после удара, как и его горизонтальная скорость, и мяч продвигается вверх, возможно, даже превышая его первоначальную высоту. Также возможно, что мяч начнет вращаться в противоположном направлении и даже отскочит назад.
Если мяч продвигается вперед с помощью topspin, поступательное и вращательное трение будет действовать в противоположные направления. Что именно происходит, зависит от того, какой из двух компонентов преобладает.
1. Если мяч вращается намного быстрее, чем он двигался, трение вращения будет преобладать. После удара угловая скорость мяча уменьшится, но его горизонтальная скорость увеличится. Мяч будет продвигаться вперед, но не превысит свою первоначальную высоту и продолжит вращаться в том же направлении.
2. Если мяч движется намного быстрее, чем он вращался, поступательное трение будет преобладать. После удара угловая скорость мяча увеличится, но его горизонтальная скорость уменьшится. Мяч не превысит свою первоначальную высоту и будет продолжать вращаться в том же направлении.

Если поверхность наклонена на некоторую величину θ, вся диаграмма будет повернута на θ, но сила тяжести останется направленной вниз (образуя угол θ с поверхностью). Тогда гравитация будет иметь компонент, параллельный поверхности, который будет способствовать трению и, таким образом, способствовать вращению.

В видах спорта с ракеткой, таких как настольный теннис или ракетбол, опытные игроки будут использовать вращение (в том числе), чтобы внезапно изменить направление мяча, когда он ударяется о поверхность, такую как земля или ракетка соперника.

Несферические мячи

Действующие силы на футбольный мяч gridiron или мяч для регби при ударе действуют сила тяжести, нормальная сила и сила трения. Трение обычно имеет «продольный» компонент из-за скорости мяча и «кувыркающего» вращения и «боковой» компонент из-за «осевого» вращения мяча, вызванного броском.

Отскок овала -образный мяч (например, используемый в футболе с сеткой или футболе по регби ), как правило, гораздо менее предсказуем, чем отскок сферического мяча. В зависимости от выравнивания мяча при ударе, нормальная сила может действовать впереди или позади центра масс мяча, а трение от земли будет зависеть от выравнивание мяча, а также его вращение, вращение и скорость удара. Когда силы, действующие по отношению к центру масс мяча, изменяются, когда мяч катится по земле, и все силы могут оказывать на мяч крутящий момент, включая нормальную силу и силу тяжести. Это может привести к тому, что мяч отскочит вперед, отскочит назад или вбок. Поскольку можно преобразовать некоторую кинетическую энергию вращения в кинетическую энергию поступательного движения, возможно, что COR будет больше 1 или скорость движения мяча может увеличиться при ударе.

Множественные уложенные друг на друга шары

Внешнее видео
Physics Girl (2015). "Шариковая капля". YouTube.

Популярная демонстрация включает в себя отскок нескольких уложенных стопкой шаров. Если теннисный мяч сложен поверх баскетбольного мяча, и оба из них упадут одновременно, теннисный мяч отскочит намного выше, чем при падении сам по себе, даже превышая исходную высоту выброса. Результат удивителен, поскольку он явно нарушает закон сохранения энергии. Однако при ближайшем рассмотрении баскетбольный мяч не подпрыгивает так высоко, как если бы теннисный мяч не находился на нем, а передавал часть своей энергии теннисному мячу, поднимая его на большую высоту.

Обычное объяснение включает рассмотрение двух отдельных ударов: удар баскетбольного мяча об пол, а затем удар баскетбольного мяча теннисным мячом. Предполагая идеально упругие столкновения, баскетбольный мяч, ударяющийся об пол со скоростью 1 м / с, отскочит со скоростью 1 м / с. У теннисного мяча, движущегося со скоростью 1 м / с, будет относительная скорость удара 2 м / с, что означает, что он отскочит со скоростью 2 м / с относительно баскетбольного мяча или 3 м / с относительно пола и утроит его. скорость отскока по сравнению с собственным ударом об пол. Это означает, что мяч отскочит от своей первоначальной высоты в 9 раз. На самом деле, из-за неупругих столкновений теннисный мяч будет увеличивать свою скорость и высоту отскока в меньшем количестве, но все же будет отскакивать быстрее и выше, чем сам по себе.

Хотя предположения об отдельных ударах на самом деле не верны (шары остаются в тесном контакте друг с другом в течение большей части удара), эта модель, тем не менее, воспроизводит экспериментальные результаты с хорошим согласием и часто используется для понимания более сложных явлений, таких как коллапс ядра сверхновой, или маневры гравитационной рогатки.

Спортивные правила

Некоторые спортивные руководящие органы регулируют подвижность мяч различными способами, прямыми и косвенными.

AFL : регулирует манометрическое давление футбольного мяча в диапазоне от 62 кПа до 76 кПа.
FIBA : регулирует манометрическое давление, чтобы баскетбольный мяч отскакивает от 1200 мм до 1400 мм (верхняя часть мяча) при падении с высоты 1800 мм (нижняя часть мяча). Это примерно соответствует COR от 0,727 до 0,806.
FIFA : регулирует манометрическое давление футбольного мяча в диапазоне от 0,6 атм до 1,1 атм при уровень моря (от 61 до 111 кПа ).
FIVB : регулирует манометрическое давление волейбольного мяча в диапазоне от 0,30 kgF / см до 0,325 кг F / см (от 29,4 до 31,9 кПа) для внутреннего волейбольного мяча и от 0,175 kgF / см до 0,225 кг F / см (от 17,2 до 22,1 кПа) для пляжный волейбол.
ITF : регулирует высоту отскока теннисного мяча при падении на «гладкий, жесткий и горизонтальный блок большой массы». Разные типы мячей допускаются для разных При падении с высоты 100 дюймов (254 см) отскок должен составлять 54–60 дюймов (137–152 см) для мячей типа 1, 53–58 дюймов (135–147 см) для мячей типа 2 и Мячи типа 3 и 48–53 дюйма (122–135 см) для мячей для высокогорья. Это примерно соответствует COR 0,735–0,775 (мяч типа 1), 0,728–0,762 (мячи типов 2 и 3) и 0,693– 0,728 (Высотные мячи) при падении на испытательную поверхность.
ITTF : регулирует игровую поверхность так, что мяч для настольного тенниса отскакивает примерно на 23 см при падении с высоты 30 см. Это примерно соответствует коэффициенту COR около 0,876 относительно игровой поверхности.
NBA : регулирует манометрическое давление баскетбольного мяча в пределах от 7,5 до 8,5 psi (51,7 до 58,6 кПа).
NFL : регулирует манометрическое давление американского футбола в диапазоне от 12,5 до 13,5 фунтов на квадратный дюйм (от 86 до 93 кПа).
RA / USGA : напрямую ограничивает COR мяча для гольфа, который не должен превышать 0,83 против клюшки для гольфа.

Давление американского футбола было в центре deflategate полемика. Некоторые виды спорта не регулируют прыгающие свойства мячей напрямую, а вместо этого определяют метод конструкции. В бейсбол введение мяча на основе пробки помогло положить конец эре мертвого мяча и запустить эру живого мяча.

См. Также

Примечания

Ссылки

Дополнительная литература

Briggs, LJ (1945). «Методы измерения коэффициента восстановления и вращения мяча». Журнал исследований Национального бюро стандартов. 34(1): 1–23. doi : 10.6028 / jres.034.001.
Кросс, Р. (2011). Физика бейсбола и софтбола. Спрингер. ISBN 978-1-4419-8112-7.
Кросс, Р. (июнь 2014 г.). «Физика отскока». Сиднейский университет.
Кросс, Р. (2015). «Поведение прыгающего мяча». Физическое образование. 50(3): 335–341. Bibcode : 2015PhyEd..50..335C. doi : 10.1088 / 0031-9120 / 50/3/335.
Стронге, У. Дж. (2004). Механика удара. Издательство Кембриджского университета. ISBN 978-0-521-60289-1.
Эрлихсон, Герман (1983). «Максимальная дальность полета снаряда с сопротивлением и подъемной силой, особенно применительно к гольфу». Американский журнал физики. 51(4): 357–362. Bibcode : 1983AmJPh..51..357E. doi : 10,1119 / 1,13248. Краткое содержание - Forbes.com (29 апреля 2013 г.)