Функция Бесселя

Семейства решений связанных дифференциальных уравнений Функции Бесселя - это радиальная часть форм колебаний кругового барабана.

Функции Бесселя, сначала выступ математиком Даниэлем Бернулли, объединенные Фридрихом Бесселем, являются каноническими решениями y (x) дифференциального уравнения Бесселя

$Икс\; 2\; d\; 2\; ydx\; 2\; +\; xdydx\; +\; (x\; 2\; -\; \alpha \; 2)\; y\; =\; 0\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; y\}\; \{dx\; ^\; \{2\}\}\}\; +\; x\; \{\backslash \; frac\; \{dy\}\; \{dx\}\}\; +\; \backslash \; left\; (x\; ^\; \{2\}\; -\; \backslash \; alpha\; ^\; \{2\}\; \backslash \; right)\; y\; =\; 0\}$

для произвольного комплексного числа α, порядок функции Бесселя. Хотя α и −α используют одно и то же дифференциальное уравнение, определяют разные функции для этих двух значений таким образом, чтобы функции Бесселя в основном были гладкими функциями α.

Наиболее важные случаи, когда α является целым числом или полуцелым числом. Функции Бесселя для целого числа α также известны как цилиндрические функции или цилиндрические гармоники, они появляются в решении уравнения Лапласа в цилиндрические координаты. Сферические функции Бесселя с полуцелым числом α получаются, когда уравнение Гельмгольца решается в сферических координатах.

• 1 Функции Бесселя
• 2 Определения
  • 2.1 Функции Бесселя первого рода: J α
    • 2.1.1 Интегралы Бесселя
    • 2.1.2 Связь с гипергеометрическими рядами
    • 2.1.3 Связь с полиномами Лагерра
  • 2.2 Функции Бесселя второго рода: Y α
  • 2.3 Функции Ганкеля: H α, H α
  • 2.4 Модифицированные функции Бесселя: I α, K α
  • 2.5 Сферические функции Бесселя: j n, y n
    • 2.5.1 Производящая функция
    • 2.5.2 Дифференциальные отношения
  • 2.6 Сферические функции Ганкеля: h n, h n
  • 2.7 Функции Риккати - Бесселя: S n, C n, ξ n, ζ n
• 3 Asy Мптотические формы
• 4 Полнообластные приближения с элементарными функциями
• 5 Свойства
  • 5.1 Рекуррентные соотношения
• 6 Теорема умножения
• 7 Нули функции Бесселя
  • 7.1 Гипотеза Бурже
  • 7.2 Численные подходы
• 8 См. Также
• 9 Примечания
• 10 Ссылки
• 11 Внешние ссылки

Уравнение Бесселя возникает при нахождении разделимых решений уравнения уравнения Лапласа и уравнение Гельмгольца в цилиндрических или сферических координатах. Поэтому функции Бесселя особенно важны для многих задач распространение волн и статических потенциалов. При решении задач в цилиндрических системах получаются функции Бесселя целого порядка (α = n); в сферических задачах получаются полуцелые порядки (α = n + 1/2). Например:

• Электромагнитные волны в цилиндрическом волноводе
• Амплитуды давления невязких вращательных потоков
• Теплопроводность в цилиндрическом объекте
• Режимы вибрации тонкой круглой (или кольцевой) акустической мембраны (например, барабана или другого мембранофона )
• Проблемы диффузии на решетке
• Решения радиального уравнения Шредингера (в сферических и цилиндрических координатах) для частиц
• Решение структурного акустического излучения
• Частотно-зависимое трение в круглых трубопроводах
• Динамика плавающих тел
• Угловое разрешение
• Дифракция от спиральных объектов, включая ДНК
• Функция плотности вероятности произведения двух нормально распределенных случайных величин

Также функции Бесселя появляются в других задачах, таких как обработка сигналов (например, см. FM -синтез, окно Кайзера или фильтр Бесселя ).

Определения это линейное дифференциальное уравнение второго порядка, должно быть два линейно независимых решений. Однако в зависимости от обстоятельств удобны различные составы этих растворов. Различные варианты приведены в таблице ниже и в следующих разделах.

Тип	Первый вид	Второй вид
Функции Бесселя	Jα	Yα
Модифицированные функции Бесселя	Iα	Kα
Функции Ханкеля	H. α= J α + iY α	H. α= J α - iY α
Сферические функции Бесселя	jn	yn
Сферические функции Ганкеля	h. n= j n + iy n	h. n= j n - iy n

Функции Бесселя второго рода и сферические функции Бесселя второго рода иногда обозначаются N n и n n соответственно, а не Y n и y n.

Функции Бесселя первого рода: J α

Функции Бесселя первого рода, обозначенные как J α (x), являются решениями дифференциального уравнения Бесселя, которые являются конечными в начале координат (x = 0) для целого или положительного α и расходятся, когда x приближается к нулю для отрицательного нецелого числа α. Функцию можно определить по ее разложению в ряду вокруг x = 0, которое можно найти, применив метод Фробениуса к уравнению Бесселя:

$J\; \alpha \; (x)\; =\; \sum \; m\; =\; 0\; \infty \; (-\; 1)\; мм!\; \Gamma \; (м\; +\; \alpha \; +\; 1)\; (Икс\; 2)\; 2\; м\; +\; \alpha ,\; \{\backslash \; Displaystyle\; J\; \_\; \{\backslash \; альфа\}\; (х)\; =\; \backslash \; сумма\; \_\; \{м\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{м\}\}\; \{м!\; \backslash \; Gamma\; (m\; +\; \backslash \; alpha\; +1)\}\}\; \{\backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\}\; ^\; \{2m\; +\; \backslash \; alpha\},\}$

где Γ (z) - это гамма -функция , сдвинутое обобщение функций факториала на нецелочисленные значения. Функция Бесселя первого рода является целой функцией, если α является целым числом, в результате этого многозначная функция с сингулярностью в нуле. Графики функций Бесселя выглядят примерно как осциллирующие синусоидальные или косинусные функции, которые убивают пропорционально $x\; -\; 1\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}$(см. также их асимптотические формы ниже), хотя их корни в общем случае не периодичны, за исключением асимптотики для больших x. (Ряд указывает, что −J 1 (x) является производной от J 0 (x), так же как −sin x является производной от cos x; в более общем смысле, производная из J n (x) может быть выражено через J n ± 1 (x) тождествами ниже.)

График функции Бесселя первого рода, J α (x), для целых порядков α = 0, 1, 2

Для нецелых α функций J α (x) и J −α (x) линейно независимы и, следовательно, являются решения двух дифференциальных уравнений. С другой стороны, для целого порядка n справедливо следующее соотношение (гамма-функция имеет простые полюсы при каждом из неположительных целых чисел):

$J\; -\; n\; (x)\; =\; (-\; 1)\; n\; J\; n\; (Икс).\; \{\backslash \; displaystyle\; J\; \_\; \{-\; n\}\; (x)\; =\; (-\; 1)\; ^\; \{n\}\; J\_\; \{n\}\; (x).\}$

Это означает, что два решения больше не являются линейно независимыми. В этом случае вторым линейно независимым решением оказывается функция Бесселя второго рода, как обсуждается ниже.

Интегралы Бесселя

Другое определение функции Бесселя для целых значений, возможно с использованием интегрального представления:

$J\; n\; (x)\; =\; 1\; \pi \; \int \; 0\; \pi \; cos\; \; (n\; \tau \; -\; x\; sin\; \; \tau )\; d\; \tau .\; \{\backslash \; displaystyle\; J\_\; \{n\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; \backslash \; cos\; (n\; \backslash \; tau\; -x\; \backslash \; sin\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau.\}$

Другое интегральное представление:

$J\; n\; (x)\; =\; 1\; 2\; \pi \; \int \; -\; \pi \; \pi \; ei\; (x\; sin\; \; \tau \; -\; n\; \tau )\; d\; \tau .\; \{\backslash \; displaystyle\; J\_\; \{n\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; pi\}\; ^\; \{\backslash \; pi\}\; e\; ^\; \{i\; (x\; \backslash \; sin\; \backslash \; tau\; -n\; \backslash \; tau)\}\; \backslash ,\; d\; \backslash \; tau.\}$

Это был подход, который использовал Бессель, и из этого определения он вывел несколько функций функций. Определение может быть расширено на нецелые порядки с помощью одного из интегралов Шлефли, для Re (x)>0:

$J\; \alpha \; (x)\; =\; 1\; \pi \; \int \; 0\; \pi \; cos\; \; (\alpha \; \tau \; -\; x\; sin\; \; \tau )\; d\; \tau \; -\; sin\; \; \alpha \; \pi \; \pi \; \int \; 0\; \infty \; e\; -\; x\; sinh\; \; t\; -\; \alpha \; tdt.\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; \backslash \; cos\; (\backslash \; alpha\; \backslash \; tau\; -x\; \backslash \; sin\; \backslash \; tau)\; \backslash ,\; d\; \backslash \; tau\; -\; \{\backslash \; frac\; \{\backslash \; sin\; \backslash \; alpha\; \backslash \; pi\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; x\; \backslash \; sinh\; t-\; \backslash \; alpha\; t\}\; \backslash ,\; dt.\}$

Связь с гипергеометрическим рядом

Функции Бесселя можно выразить через обобщенный гипергеометрический ряд as

$J\; \alpha \; (x)\; =\; (x\; 2)\; \alpha \; \Gamma \; (\alpha \; +\; 1)\; 0\; F\; 1\; (\alpha \; +\; 1;\; -\; х\; 2\; 4).\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\}\}\; \backslash ;\; \_\; \{0\}\; F\_\; \{1\}\; \backslash \; left\; (\backslash \; alpha\; +1;\; -\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right).\}$

Это связано с разработкой функций Бесселя в терминах функции Бесселя - Клиффорда.

Связь с полиномами Лагерра

В терминах полиномов Лагерра Lkи произвольно выбранные программы t функция Бесселя может быть выражена как

$J\; \alpha \; (x)\; (x\; 2)\; \alpha \; знак\; равно\; e\; -\; t\; \Gamma \; (\alpha \; +\; 1)\; \sum \; k\; =\; 0\; \infty \; L\; k\; (\alpha )\; (x\; 2\; 4\; t)\; (k\; +\; \alpha \; k)\; tkk!.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{J\; \_\; \{\backslash \; alpha\}\; (x)\}\; \{\backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\}\}\; =\; \{\backslash \; frac\; \{e\; ^\; \{-\; t\}\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{L\_\; \{k\}\; ^\; \{(\backslash \; alpha)\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{4t\}\}\; \backslash \; right)\}\; \{\backslash \; binom\; \{k\; +\; \backslash \; alpha\}\; \{k\}\}\}\; \{\backslash \; frac\; \{t\; ^\; \{k\}\}\; \{k!\}\}.\}$

Функции Бесселя второго kind: Y α

Функции Бесселя второго рода, обозначаемые Y α (x), иногда вместо этого обозначаемые N α (x), являются решениями дифференциала Бесселя уравнение, которое имеет особенность в начало координат (x = 0) и является многозначным. Иногда их называют функции Вебера, так как они были введены H. М. Вебер (1873), а также функции Неймана после Карла Неймана.

График функции Бесселя второго рода, Y α (x), для целочисленных порядков α = 0, 1, 2

Для нецелого числа α Y α (x) связано с J α (x) по

$Y\; \alpha \; (x)\; =\; J\; \alpha \; (x)\; cos\; \; (\alpha \; \pi )\; -\; J\; -\; \alpha \; (x)\; sin\; \; (\alpha \; \pi ).\; \{\backslash \; Displaystyle\; Y\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{J\; \_\; \{\backslash \; alpha\}\; (x)\; \backslash \; cos\; (\backslash \; alpha\; \backslash \; pi)\; -J\; \_\; \{-\; \backslash \; alpha\}\; (x)\}\; \{\backslash \; sin\; (\; \backslash \; alpha\; \backslash \; pi)\}\}.\}$

В случае целого порядка n функция достигается путем взятия предела, когда нецелое число α к n:

$Y\; n\; (x)\; =\; lim\; \alpha \; \to \; n\; Y\; \alpha \; (Икс).\; \{\backslash \; displaystyle\; Y\_\; \{n\}\; (x)\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; n\}\; Y\; \_\; \{\backslash \; alpha\}\; (x).\}$

Если n - неотрицательное целое число, мы имеем ряд

$Y\; n\; (г)\; знак\; равно\; -\; (г\; 2)\; -\; N\; \pi \; \sum \; К\; знак\; равно\; 0\; N\; -\; 1\; (N\; -\; К\; -\; 1)!\; к!\; (z\; 2\; 4)\; k\; +\; 2\; \pi \; J\; n\; (z)\; ln\; \; z\; 2\; -\; (z\; 2)\; n\; \pi \; \sum \; k\; =\; 0\; \infty \; (\psi \; (k\; +\; 1)\; +\; \psi \; (n\; +\; k\; +\; 1))\; (-\; z\; 2\; 4)\; кк!\; (п\; +\; к)!\; \{\backslash \; displaystyle\; Y\_\; \{n\}\; (z)\; =\; -\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{-\; n\}\}\; \{\backslash \; pi\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\; \}\; ^\; \{n-1\}\; \{\backslash \; frac\; \{(nk-1)!\}\; \{k!\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; ^\; \{k\}\; +\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\; J\_\; \{n\}\; (z)\; \backslash \; ln\; \{\backslash \; frac\; \{z\}\; \{2\}\}\; -\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{n\}\}\; \{\backslash \; pi\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; (\backslash \; psi\; (k\; +\; 1)\; +\; \backslash \; psi\; (n\; +\; k\; +\; 1))\; \{\backslash \; frac\; \{\backslash \; left\; (-\; \{\; \backslash \; frac\; \{z\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; ^\; \{k\}\}\; \{к!\; (n\; +\; k)!\}\}\}$

где $\psi \; (z)\; \{\backslash \; displaystyle\; \backslash \; psi\; (z)\}$- дигамма-функция, логарифмическая производная от гамма-.

Существует также соответствующая функция интегральной формулы (для Re (x)>0):

$Y\; n\; (x)\; =\; 1\; \pi \; \int \; 0\; \pi \; sin\; \; (x\; sin\; \; \theta \; -\; n\; \theta )\; d\; \theta \; -\; 1\; \pi \; \int \; 0\; \infty \; (ent\; +\; (-\; 1)\; ne\; -\; nt)\; е\; -\; х\; з\; тдт.\; \{\backslash \; displaystyle\; Y\_\; \{n\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; \backslash \; sin\; (x\; \backslash \; sin\; \backslash \; theta\; -n\; \backslash \; theta)\; \backslash ,\; d\; \backslash \; theta\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (e\; ^\; \{nt\}\; +\; (-\; 1)\; ^\; \{n\}\; e\; ^\; \{-\; nt\}\; \backslash \; right)\; e\; ^\; \{-\; x\; \backslash \; sh\; t\}\; \backslash ,\; dt.\}$

Yα(x) необходимо как второе линейно независимое решение уравнения Бесселя, когда α является целым числом. Но Y α (x) имеет большее значение, чем это. Его можно рассматривать как «естественного» партнера J α (x). См. Также подраздел о функциях Ганкеля ниже.

Когда α является целым числом, кроме того, как было аналогично для функций первого рода, справедливо следующее соотношение:

$Y\; -\; n\; (x)\; =\; (-\; 1)\; n\; Y\; n\; (Икс).\; \{\backslash \; displaystyle\; Y\; \_\; \{-\; n\}\; (x)\; =\; (-\; 1)\; ^\; \{n\}\; Y\_\; \{n\}\; (x).\}$

И J α (x), и Y α (x) - голоморфные функции от x на комплексной плоскости, разрезанной вдоль отрицательной действительной оси. Когда α является целым числом, функции Бесселя J являются целыми функциями от x. Если x удерживается фиксированным на ненулевом значении, то Бесселя выполняет целые функции от α.

Функции Бесселя второго рода, когда одним из основных примеров решения типа в теореме Фукса.

Функции Ганкеля: H. α, H. α

Еще одна важная формулировка двух линейно независимых решения уравнения Бесселя являются функции Ганкеля первого и второго рода, H. α(x) и H. α(x), определяемые как

$H\; \alpha \; (1)\; (Икс)\; знак\; равно\; J\; \alpha \; (Икс)\; +\; я\; Y\; \alpha \; (Икс),\; ЧАС\; \alpha \; (2)\; (Икс)\; =\; J\; \alpha \; (Икс)\; -\; я\; Y\; \alpha \; (Икс),\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; H\; \_\; \{\backslash \; alpha\}\; ^\; \{\; (1)\}\; (x)\; =\; J\; \_\; \{\backslash \; alpha\}\; (x)\; +\; iY\; \_\; \{\backslash \; alpha\}\; (x),\; \backslash \backslash \; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(2)\}\; (x)\; =\; J\; \_\; \{\backslash \; alpha\}\; (x)\; -iY\; \_\; \{\backslash \; alpha\}\; (x),\; \backslash \; end\; \{align\}\}\}$

, где i - мнимая единица. Эти линейные комбинации также известны как функции Бесселя третьего рода ; они являются двумя линейно независимыми решениями дифференциального уравнения Бесселя. Они названы в честь Германа Ганкеля.

. Эти формы линейной комбинации представлены многочисленным на первый взгляд простых свойств, такими как асимптотические формулы или интегральные представления. Здесь «простой» появление фактора формы e. Таким образом, можно думать, что функция Бесселя второго рода естественным образом возникает как мнимая часть функций Ганкеля.

Функции Ханкеля используются для выражения решений цилиндрических волн, распространяющихся наружу и внутрь, уравнения цилиндрической волны, соответственно (или наоборот, в зависимости от знака для частота ).

Используя предыдущие соотношения, их можно выразить как

$H\; \alpha \; (1)\; (x)\; =\; J\; -\; \alpha \; (x)\; -\; e\; -\; \alpha \; \pi \; i\; J\; \alpha \; (x)\; i\; sin\; \; \alpha \; \pi ,\; H\; \alpha \; (2)\; (x)\; =\; J\; -\; \alpha \; (x)\; -\; e\; \alpha \; \pi \; i\; J\; \alpha \; (x)\; -\; i\; sin\; \; \alpha \; \pi .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(1)\}\; (x)\; =\; \{\backslash \; frac\; \{J\; \_\; \{-\; \backslash \; alpha\}\; (x)\; -e\; ^\; \{-\; \backslash \; alpha\; \backslash \; pi\; i\; \}\; J\_\; \{\backslash \; alpha\}\; (x)\}\; \{i\; \backslash \; sin\; \backslash \; alpha\; \backslash \; pi\}\},\; \backslash \backslash \; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(2)\}\; (x)\; =\; \{\backslash \; frac\; \{J\; \_\; \{-\; \backslash \; alpha\; \}\; (x)\; -e\; ^\; \{\backslash \; alpha\; \backslash \; pi\; i\}\; J\; \_\; \{\backslash \; alpha\}\; (x)\}\; \{-\; i\; \backslash \; sin\; \backslash \; alpha\; \backslash \; pi\}\}.\; \backslash \; end\; \{align\}\}\}$

Если α - целое число, предел имеет быть рассчитанным. Следующие соотношения действительны, независимо от того, являются ли α целым или нет:

$H\; -\; \alpha \; (1)\; (x)\; =\; e\; \alpha \; \pi \; i\; H\; \alpha \; (1)\; (x),\; H\; -\; \alpha \; (2)\; (x)\; =\; е\; -\; \alpha \; \pi \; i\; H\; \alpha \; (2)\; (x).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; H\; \_\; \{-\; \backslash \; alpha\}\; ^\; \{(1)\}\; (x)\; =\; e\; ^\; \{\backslash \; alpha\; \backslash \; pi\; i\}\; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(1)\}\; (x),\; \backslash \backslash \; H\; \_\; \{-\; \backslash \; alpha\}\; ^\; \{(2)\}\; (x)\; =\; e\; ^\; \{-\; \backslash \; alpha\; \backslash \; pi\; i\}\; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(2)\}\; (x).\; \backslash \; End\; \{align\}\}\}$

В частности, если α = m + 1/2 с ma неотрицательным целым числом, из приведенных выше указанных прямо следует, что

$J\; -\; (m\; +\; 1\; 2)\; (x)\; =\; (-\; 1)\; m\; +\; 1\; Y\; m\; +\; 1\; 2\; (х),\; Y\; -\; (м\; +\; 1\; 2)\; (х)\; =\; (-\; 1)\; м\; Дж\; м\; +\; 1\; 2\; (х).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; J\; \_\; \{-\; (m\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\}\; (x)\; =\; (-\; 1)\; ^\; \{m\; +\; 1\}\; Y\_\; \{m\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x),\; \backslash \backslash \; Y\; \_\; \{-\; (m\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\}\; (x)\; =\; (-\; 1)\; ^\; \{m\}\; J\_\; \{m\; +\; \{\backslash \; frac\; \{1\})\; \{2\}\}\}\; (х).\; \backslash \; End\; \{align\}\}\}$

Они полезны при разработке сферических функций Бесселя (см. Ниже).

Функции Ганкеля допускают следующие интегральные представления для Re (x)>0:

$H\; \alpha \; (1)\; (x)\; =\; 1\; \pi \; i\; \int \; -\; \infty \; +\; \infty \; +\; i\; \pi \; ex\; sinh\; \; t\; -\; \alpha \; tdt,\; ЧАС\; \alpha \; (2)\; (Икс)\; знак\; равно\; -\; 1\; \pi \; я\; \int \; -\; \infty \; +\; \infty \; -\; я\; \pi \; ex\; sinh\; \; T\; -\; \alpha \; tdt,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(1)\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; i\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{+\; \backslash \; infty\; +\; i\; \backslash \; pi\}\; e\; ^\; \{x\; \backslash \; sinh\; t-\; \backslash \; alpha\; t\}\; \backslash ,\; dt,\; \backslash \backslash \; H\; \_\; \{\backslash \; alpha\}\; ^\; \{(2)\}\; (x)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; i\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{+\; \backslash \; infty\; -i\; \backslash \; pi\}\; e\; ^\; \{x\; \backslash \; sinh\; t-\; \backslash \; alpha\; t\}\; \backslash ,\; dt,\; \backslash \; end\; \{align\}\}\}$

где пределы интегрирования укажите интегрирование вдоль контура , который можно выбрать следующим образом: от −∞ до 0 по отрицательной действительной оси, от 0 до ± iπ по мнимой оси и от ± iπ до + ∞ ± iπ по контуру, параллельному действительной оси.

Модифицированные функции Бесселя: I α, K α

Функции Бесселя действительны даже для сложных аргументов x, важный частный случай является случай чисто мнимого аргумента. В этом случае решения уравнения Бесселя называются модифицированные функции Бесселя (или иногда гиперболические функции Бесселя ) первого и второго рода и имеют значение как

$I\; \alpha \; (x)\; знак\; равно\; я\; -\; \alpha \; J\; \alpha \; (ix)\; знак\; равно\; \sum \; м\; знак\; равно\; 0\; \infty \; 1\; м!\; \Gamma \; (m\; +\; \alpha \; +\; 1)\; (x\; 2)\; 2\; m\; +\; \alpha ,\; K\; \alpha \; (x)\; =\; \pi \; 2\; I\; -\; \alpha \; (x)\; -\; I\; \alpha \; (x)\; sin\; \; \alpha \; \pi ,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено)\; \}\; I\; \_\; \{\backslash \; alpha\}\; (x)\; =\; i\; ^\; \{-\; \backslash \; alpha\}\; J\; \_\; \{\backslash \; alpha\}\; (ix)\; =\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{m\; !\; \backslash ,\; \backslash \; Gamma\; (m\; +\; \backslash \; alpha\; +1)\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; ^\; \{2m\; +\; \backslash \; alpha\},\; \backslash \backslash \; K\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \{\backslash \; frac\; \{I\; \_\; \{-\; \backslash \; alpha\}\; (x)\; -I\; \_\; \{\backslash \; alpha\}\; (x)\}\; \{\backslash \; sin\; \backslash \; alpha\; \backslash \; pi\}\},\; \backslash \; end\; \{\; align\}\}\}$

когда α не целое; когда α - целое число, используется предел. Они выбраны с действительными значениями для действительных и положительных аргументов x. Таким образом, разложение в ряд для I α (x) аналогично разложению для J α (x), но без переменного (-1) множителя.

$K\; \alpha \; \{\backslash \; displaystyle\; K\; \_\; \{\backslash \; alpha\}\}$можно выразить через функции Ганкеля:

Мы можем выразить первую и вторую функции Бесселя через модифицированные функции Бесселя (они верны, если −π < arg z ≤ π/2):

$J\; \alpha \; (iz)\; =\; e\; \alpha \; i\; \pi \; 2\; I\; \alpha \; (z),\; Y\; \alpha \; (iz)\; знак\; равно\; е\; (\alpha \; +\; 1)\; я\; \pi \; 2\; я\; \alpha \; (z)\; -\; 2\; \pi \; е\; -\; \alpha \; я\; \pi \; 2\; К\; \alpha \; (z).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; J\; \_\; \{\backslash \; альфа\}\; (iz)\; =\; e\; ^\; \{\backslash \; frac\; \{\backslash \; alpha\; i\; \backslash \; pi\}\; \{2\}\}\; I\; \_\; \{\backslash \; alpha\}\; (z),\; \backslash \backslash \; Y\; \_\; \{\backslash \; alpha\}\; (iz)\; =\; e\; ^\; \{\backslash \; frac\; \{(\backslash \; alpha\; +1)\; i\; \backslash \; pi\}\; \{2\}\}\; I\; \_\; \{\backslash \; alpha\}\; (z)\; -\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{\backslash \; alpha\; i\; \backslash \; pi\}\; \{2\}\}\}\; K\_\; \{\backslash \; alpha\}\; (z).\; \backslash \; end\; \{align\}\}\}$

Iα(x) и K α (x) - два линейно независимых решения модифицированного уравнения Бесселя :

$x\; 2\; d\; 2\; ydx\; 2\; +\; xdydx\; -\; (x\; 2\; +\; \alpha \; 2)\; y\; =\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; y\}\; \{dx\; ^\; \{2\}\}\}\; +\; x\; \{\backslash \; frac\; \{dy\}\; \{dx\}\}\; -\; \backslash \; left\; (x\; ^\; \{2\}\; +\; \backslash \; alpha\; ^\; \{2\}\; \backslash \; right)\; y\; =\; 0.\}$

В отличие от обычных функций Бесселя, которые колеблются как функции дей ствительного аргумента, I α и K α - это экспоненциально растущие и убывающие функции соответственно. Как и обычная функция Бесселя J α, функция I α стремится к нулю при x = 0 при α>0 и конечна при x = 0 при α = 0. Аналогично, K α расходится при x = 0 с особенностью логарифмического типа для K 0 и ½Γ (| α |) (2 / x) в случае.

Модифицированные функции Бесселя первого рода, I α (x), для α = 0, 1, 2, 3

Модифицированные функции Бесселя второго рода, K α (x), для α = 0, 1, 2, 3

. Две интегральные формулы для модифицированных функций Бесселя (для Re (x)>0):

$I\; \alpha \; (x)\; =\; 1\; \pi \; \int \; 0\; \pi \; ex\; cos\; \; \theta \; cos\; {\rm A}\; \theta \; d\; \theta \; -\; sin\; \; \alpha \; \pi \; \pi \; \int \; 0\; \infty \; e\; -\; x\; ch\; \; t\; -\; \alpha \; tdt,\; K\; \alpha \; (x)\; =\; \int \; 0\; \infty \; e\; -\; x\; ch\; \; t\; ch\; \; \alpha \; tdt.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; I\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; pi\}\; e\; ^\; \{x\; \backslash \; cos\; \backslash \; theta\; \}\; \backslash \; cos\; \backslash \; alpha\; \backslash \; theta\; \backslash ,\; d\; \backslash \; theta\; -\; \{\backslash \; frac\; \{\backslash \; sin\; \backslash \; alpha\; \backslash \; pi\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; x\; \backslash \; ch\; t-\; \backslash \; альфа\; t\}\; \backslash ,\; dt,\; \backslash \backslash \; K\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; x\; \backslash \; ch\; t\}\; \backslash \; cosh\; \backslash \; alpha\; t\; \backslash ,\; dt.\; \backslash \; end\; \{выровнены\}\}\}$

Функции Бесселя можно описать как преобразование Фурье степеней квадратичных функций. Например:

$2\; K\; 0\; (\omega )\; =\; \int \; -\; \infty \; \infty \; e\; i\; \omega \; t\; t\; 2\; +\; 1\; d\; t.\; \{\backslash \; displaystyle\; 2\; \backslash ,\; K\_\; \{0\}\; (\backslash \; omega)\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{e\; ^\; \{я\; \backslash \; omega\; t\}\}\; \{\backslash \; sqrt\; \{t\; ^\; \{2\}\; +1\}\}\}\; \backslash ,\; dt.\}$

Это можно доказать равенство приведенному выше определению интеграла для K 0. Это делается путем интегрирования замкнутой кривой в первом квадранте комплексной плоскости.

Модифицированные функции Бесселя K 1/3 и K 2/3 могут быть представлены в виде быстро сходящихся интегралов

$K\; 1\; 3\; (\xi )\; =\; 3\; \int \; 0\; \infty \; exp\; \; (-\; \xi \; (1\; +\; 4\; x\; 2\; 3)\; 1\; +\; x\; 2\; 3)\; dx,\; K\; 2\; 3\; (\xi )\; =\; 1\; 3\; \int \; 0\; \infty \; 3\; +\; 2\; x\; 2\; 1\; +\; x\; 2\; 3\; exp\; \; (-\; \xi \; (1\; +\; 4\; x\; 2\; 3)\; 1\; +\; x\; 2\; 3)\; dx.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; K\; \_\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; (\backslash \; xi)\; =\; \{\backslash \; sqrt\; \{3\}\}\; \backslash \; int\; \_\{0\}\; ^\; \{\backslash \; infty\}\; \backslash \; exp\; \backslash \; left\; (-\; \backslash \; xi\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{4x\; ^\; \{2\}\}\; \{3\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{1\; +\; \{\backslash \; frac\; \{x\; ^)\; \{2\}\}\; \{3\}\}\}\}\; \backslash \; right)\; \backslash ,\; dx,\; \backslash \backslash \; K\; \_\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; (\backslash \; xi)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{3\}\}\; \}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{3\; +\; 2x\; ^\; \{2\}\}\; \{\backslash \; sqrt\; \{1\; +\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{3\}\}\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \backslash \; xi\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{4x\; ^\; \{2\}\}\; \{3\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{1\; +\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{3\}\}\}\}\; \backslash \; вправо)\; \backslash ,\; dx.\; \backslash \; End\; \{align\}\}\}$

модифицированная функция Бесселя второго также вызывалась под именами (сейчас редко):

• функция Бассета после Альфреда Барнарда Бассета
• Модифицированная функция Бесселя третий вид
• Модифицированная функция Ханкеля
• функция Макдональда после Гектора Манро Макдональда

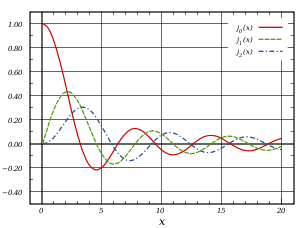Сферические функции Бесселя: j n, y n Сферические функции Бесселя первого вида, j n (x), для n = 0, 1, 2 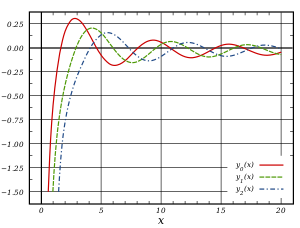Сферические функции Бесселя второго рода, y n (x), для n = 0, 1, 2

При решении уравнения Гельмгольца в сферической координате путем разделения альтернативное уравнение имеет вид

$x\; 2\; d\; 2\; ydx\; 2\; +\; 2\; xdydx\; +\; (x\; 2\; -\; n\; (n\; +\; 1))\; y\; =\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; \{\backslash \; гидроразрыв\; \{d\; ^\; \{2\}\; y\}\; \{dx\; ^\; \{2\}\}\}\; +\; 2x\; \{\backslash \; frac\; \{dy\}\; \{dx\}\}\; +\; \backslash \; left\; (x\; ^\; \{2\}\; -n\; (n\; +\; 1)\; \backslash \; right)\; y\; =\; 0.\}$

Два линейно независимых решения этого уравнения сферические функции Бесселя jnи y n и с вязаны с обычными функциями Бесселя J n и Y nby

$jn\; (x)\; =\; \pi \; 2\; x\; J\; n\; +\; 1\; 2\; (x),\; yn\; (x)\; =\; \pi \; 2\; x\; Y\; n\; +\; 1\; 2\; (x)\; =\; (-\; 1)\; n\; +\; 1\; \pi \; 2\; х\; Дж\; -\; п\; -\; 1\; 2\; (х).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; j\_\; \{n\}\; (x)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2x\}\}\}\; J\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x),\; \backslash \backslash \; y\_\; \{n\}\; (x)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2x\}\}\}\; Y\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x)\; =\; (-\; 1)\; ^\; \{n\; +\; 1\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2x\}\}\}\; J\; \_\; \{-\; n\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x).\; \backslash \; end\; \{align\}\}\}$

ynтакже обозначается n n или η n; некоторые авторы эти функции являются сферическими функциями Неймана .

Сферические функции Бесселя также могут быть записаны как (формулы Рэлея )

$jn\; (x)\; =\; (-\; x)\; n\; (1\; xddx)\; n\; sin\; \; хх,\; уn\; (х)\; =\; -\; (-\; х)\; п\; (1\; хддх)\; п\; соз\; \; хх.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; j\_\; \{n\}\; (x)\; =\; (-\; x)\; ^\; \{n\}\; \backslash \; left\; (\{\; \backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \backslash \; right)\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\}\},\; \backslash \backslash \; y\_\; \{n\}\; (x)\; =\; -\; (-\; x)\; ^\; \{n\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \backslash \; right)\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\}\; \}.\; \backslash \; end\; \{align\}\}\}$

Первая сферическая функция Бесселя j 0 (x) также известна как (ненормализованная) функция sinc. Первые сферические функции Бесселя являются:

$j\; 0\; (x)\; =\; sin\; \; xx.\; J\; 1\; (x)\; =\; sin\; \; xx\; 2\; -\; cos\; \; xx,\; j\; 2\; (x)\; =\; (3\; x\; 2\; -\; 1)\; sin\; \; xx\; -\; 3\; соз\; \; хх\; 2,\; j\; 3\; (х)\; =\; (15\; х\; 3\; -\; 6\; х)\; грех\; хх\; -\; (15\; х\; 2\; -\; 1)\; соз\; х\; хх\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; j\_\; \{0\}\; (x)\; =\; \{\backslash \; frac\; \{\; \backslash \; sin\; x\}\; \{x\}\}.\; \backslash \backslash \; j\_\; \{1\}\; (x)\; =\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{\; x\}\},\; \backslash \backslash \; j\_\; \{2\}\; (x)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{x\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\}\}\; -\; \{\backslash \; frac\; \{3\; \backslash \; cos\; x\}\; \{x\; ^\; \{2\}\}\},\; \backslash \backslash \; j\_\; \{3\}\; (x)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{15\}\; \{x\; ^\; \{3\}\}\}\; -\; \{\backslash \; frac\; \{6\}\; \{x\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\}\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{15\}\; \{x\; ^\; \{2\}\}\}\; -\; 1\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\}\}\; \backslash \; end\; \{align\}\}\}$

и

$y\; 0\; (x)\; =\; -\; j\; -\; 1\; (x)\; =\; -\; cos\; \; xx,\; y\; 1\; (x)\; =\; j\; -\; 2\; (\; x)\; =\; -\; cos\; \; xx\; 2\; -\; sin\; \; xx,\; y\; 2\; (x)\; =\; -\; j\; -\; 3\; (x)\; =\; (-\; 3\; x\; 2\; +\; 1)\; cos\; \; xx\; -\; 3\; sin\; \; xx\; 2,\; y\; 3\; (x)\; знак\; равно\; j\; -\; 4\; (x)\; =\; (-\; 15\; x\; 3\; +\; 6\; x)\; cos\; \; xx\; -\; (15\; x\; 2\; -\; 1)\; sin\; \; xx.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; y\_\; \{0\}\; (x)\; =\; -\; j\; \_\; \{-\; 1\}\; (x)\; =\; -\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\}\},\; \backslash \backslash \; y\_\; \{1\}\; (\; x)\; =\; j\; \_\; \{-\; 2\}\; (x)\; =\; -\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\}\},\; \backslash \backslash \; y\_\; \{2\; \}\; (x)\; =\; -\; j\; \_\; \{-\; 3\}\; (x)\; =\; \backslash \; left\; (-\; \{\backslash \; frac\; \{3\}\; \{x\; ^\; \{2\}\}\}\; +\; 1\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\; \}\}\; -\; \{\backslash \; frac\; \{3\; \backslash \; sin\; x\}\; \{x\; ^\; \{2\}\}\},\; \backslash \backslash \; y\_\; \{3\}\; (x)\; =\; j\; \_\; \{-\; 4\}\; (x)\; =\; \backslash \; left\; (-\; \{\backslash \; frac\; \{\; 15\}\; \{x\; ^\; \{3\}\}\}\; +\; \{\backslash \; frac\; \{6\}\; \{x\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; cos\; x\}\; \{x\}\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{15\}\; \{x\; ^\; \{\; 2\}\}\}\; -1\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; sin\; x\}\; \{x\}\}.\; \backslash \; End\; \{align\}\}\}$

Производящая функция

Сферические функции Бесселя имеют производящие функции

$1\; z\; cos\; \; (z\; 2\; -\; 2\; zt)\; знак\; равно\; \sum \; N\; знак\; равно\; 0\; \infty \; tnn!\; J\; N\; -\; 1\; (Z),\; 1\; Z\; грех\; \; (Z\; 2\; -\; 2\; Z\; T)\; знак\; равно\; \sum \; N\; знак\; равно\; 0\; \infty \; T\; N\; N!\; у\; н\; -\; 1\; (г).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{1\}\; \{z\}\}\; \backslash \; cos\; \backslash \; left\; (\{\backslash \; sqrt\; \{z\; ^\; \{2\}\; -2zt\}\}\; \backslash \; right)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{t\; ^\; \{n\}\}\; \{n!\}\}\; j\_\; \{n-1\}\; (z),\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{z\}\}\; \backslash \; sin\; \backslash \; left\; (\{\backslash \; sqrt\; \{z\; ^\; \{2\}\; -2zt\}\}\; \backslash \; right)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{t\; ^\; \{n\}\}\; \{n!\}\}\; y\_\; \{n-1\}\; (\; z).\; \backslash \; end\; \{align\}\}\}$

Дифференциальные отношения

Далее f n представляет собой любое из j n, y n, h. n, h. nдля n = 0, ± 1, ± 2,...

$(1\; zddz)\; m\; (zn\; +\; 1\; fn\; (z))\; =\; zn\; -\; m\; +\; 1\; fn\; -\; m\; (z),\; (1\; zddz)\; m\; (z\; -\; nfn\; (z))\; =\; (-\; 1)\; mz\; -\; n\; -\; mfn\; +\; m\; (z).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{z\}\}\; \{\backslash \; frac\; \{d\}\; \{dz\}\}\; \backslash \; right)\; ^\; \{m\}\; \backslash \; left\; (z\; ^\; \{n\; +\; 1\}\; f\_\; \{n\}\; (z)\; \backslash \; right)\; =\; z\; ^\; \{nm\; +\; 1\}\; f\_\; \{nm\}\; (z),\; \backslash \backslash \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{z\}\}\; \{\backslash \; frac\; \{d\}\; \{dz\}\; \}\; \backslash \; right)\; ^\; \{m\}\; \backslash \; left\; (z\; ^\; \{-\; n\}\; f\_\; \{n\}\; (z)\; \backslash \; right)\; =\; (-\; 1)\; ^\; \{m\}\; z\; ^\; \{-\; nm\}\; f\_\; \{n\; +\; m\}\; (\; z).\; \backslash \; end\; \{align\}\}\}$

Сферические функции Ганкеля: h. n, h. n

Существуют также сферические функции-аналоги Ханкеля:

$hn\; (1)\; (x)\; =\; jn\; (х)\; +\; iyn\; (x),\; hn\; (2)\; (x)\; =\; jn\; (x)\; -\; iyn\; (x).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; h\_\; \{n\}\; ^\; \{(1)\}\; (x)\; =\; j\_\; \{n\}\; (x)\; +\; iy\_\; \{n\}\; (x),\; \backslash \backslash \; h\_\; \{n\}\; ^\; \{(2)\}\; (х)\; =\; j\_\; \{n\}\; (x)\; -iy\_\; \{n\}\; (x).\; \backslash \; end\; \{align\}\}\}$

На самом деле есть простые выражения в замкнутой форме для функций Бесселя полуцелочисленный порядок в терминах стандартных тригонометрических функций и, следовательно, для сферических функций Бесселя. В частности, для неотрицательных целых чисел n:

$h\; n\; (1)\; (x)\; =\; (-\; i)\; n\; +\; 1\; e\; i\; x\; x\; \sum \; m\; =\; 0\; n\; i\; m\; m!\; (2\; х)\; м\; (п\; +\; м)!\; (п\; -\; м)!,\; \{\backslash \; displaystyle\; h\_\; \{n\}\; ^\; \{(1)\}\; (x)\; =\; (-\; i)\; ^\; \{n\; +\; 1\}\; \{\backslash \; frac\; \{e\; ^\; \{ix\}\}\; \{x\}\}\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{n\}\; \{\backslash \; frac\; \{i\; ^\; \{m\}\}\; \{м!\; \backslash ,\; (2x)\; ^\; \{m\}\}\}\; \{\backslash \; frac\; \{(n\; +\; m)!\}\; \{(Nm)!\}\},\}$

и h. n- это комплексно-сопряженное значение этого (для действительного x). Отсюда следует, например, что j 0 (x) = sin x / x и y 0 (x) = −cos x / x и так далее. мультипольном разложении электромагнитного поля.

Функции Риккати - Бесселя - Бесселя: S n мультипольном разложении электромагнитного поля

., C n, ξ n, ζ n

Riccati - функции Бесселя незначительно отличаются от сферических функций Бесселя:

$S\; n\; (x)\; =\; xjn\; (x)\; =\; \pi \; x\; 2\; J\; n\; +\; 1\; 2\; (x)\; C\; n\; (x)\; =\; -\; xyn\; (x)\; =\; -\; \pi \; x\; 2\; Y\; n\; +\; 1\; 2\; (x)\; \xi \; n\; (x)\; =\; xhn\; (1)\; (x)\; =\; \pi \; x\; 2\; H\; n\; +\; 1\; 2\; (1)\; (x)\; =\; S\; n\; (x)\; -\; i\; C\; n\; (x)\; \zeta \; n\; (x)\; =\; xhn\; (2)\; (x)\; =\; \pi \; x\; 2\; H\; n\; +\; 1\; 2\; (\; 2)\; (Икс)\; знак\; равно\; SN\; (Икс)\; +\; я\; С\; N\; (Икс)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; S\_\; \{п\}\; (х)\; =\; xj\_\; \{п\}\; (х)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\; x\}\; \{2\}\}\}\; J\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x)\; \backslash \backslash \; C\_\; \{n\}\; (x)\; =\; -\; xy\_\; \{n\}\; (x)\; =\; -\; \{\; \backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\; x\}\; \{2\}\}\}\; Y\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; (x)\; \backslash \backslash \backslash \; xi\; \_\; \{n\}\; (x)\; =\; xh\_\; \{n\}\; ^\; \{(1)\}\; (x)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\; x\}\; \{2\}\}\}\; H\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; ^\; \{(1)\}\; (x)\; =\; S\_\; \{n\}\; (x)\; -iC\_\; \{n\}\; (x)\; \backslash \backslash \backslash \; zeta\; \_\; \{n\}\; (x)\; =\; xh\_\; \{n\}\; ^\; \{\; (2)\}\; (x)\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; pi\; x\}\; \{2\}\}\}\; H\_\; \{n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; ^\; \{(2)\}\; (x)\; =\; S\_\; \{n\}\; (x)\; +\; iC\_\; \{n\}\; (x)\; \backslash \; end\; \{align\}\}\}$

Они удовлетворяют дифференциальному уравнению

$x\; 2\; d\; 2\; ydx\; 2\; +\; (x\; 2\; -\; n\; (n\; +\; 1))\; y\; Знак\; равно\; 0.\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; y\}\; \{dx\; ^\; \{2\}\}\}\; +\; \backslash \; left\; (x\; ^\; \{2\}\; -n\; (n\; +\; 1)\; \backslash \; right)\; y\; =\; 0.\}$

Например, такого рода дифференциальное уравнение появляется в квантовой механике при решении радиальной составляющей уравнения уравнения Шредингера с гипотетическим цилиндрическим бесконечным потенциальным барьером. Это дифференциальное уравнение и решения Риккати - Бесселя также задает задаче рассеяния электромагнитных волн сферой, известной как рассеяние Ми после первого решения Ми (1908). См. Например, Du (2004) для последних разработок и ссылок.

После Дебая (1909) иногда используется обозначение ψ n, χ n вместо S n, C n.

Асимптотические формы

Функции Бесселя имеют следующие асимптотические формы. Для малых аргументов 0 < z ≪ √α + 1, one obtains, when α is not a negative integer:

$J\; \alpha \; (z)\; \sim \; 1\; \Gamma \; (\alpha \; +\; 1)\; (z\; 2)\; \alpha .\; \{\backslash \; Displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (z)\; \backslash \; sim\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}.\}$

Когда α - отрицательное целое число, мы имеем

$J\; \alpha \; (z)\; \sim \; (-\; 1)\; \alpha \; (-\; \alpha )!\; (2\; z)\; \alpha .\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (z)\; \backslash \; sim\; \{\backslash \; frac\; \{(-1)\; ^\; \{\backslash \; alpha\}\}\; \{(-\; \backslash \; alpha)!\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{z\}\}\; \backslash )\; ^\; \{\backslash \; alpha\}.\}$

Для функций Бесселя второго имеет три случая справа:

$Y\; \alpha \; (z)\; \sim \; \{2\; \pi \; (ln\; \; (z\; 2)\; +\; \gamma ),\; если\; \alpha \; =\; 0\; -\; \Gamma \; (\alpha )\; \pi \; (2\; z)\; \alpha \; +\; 1\; \Gamma \; (\alpha \; +\; 1)\; (z\; 2)\; \alpha \; cot\; \; (\alpha \; \pi ),\; если\; \alpha \; не\; является\; целым\; неположительным\; числом\; (один\; член\; доминирует,\; если\; \alpha \; не\; является\; мнимым),\; -\; (-\; 1)\; \alpha \; \Gamma \; (-\; \alpha )\; \pi \; (z\; 2)\; \alpha ,\; если\; \alpha \; -\; целое\; отрицательное\; число,\; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; alpha\}\; (z)\; \backslash \; sim\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; dfrac\; \{2\}\; \{\backslash \; pi\}\}\; \backslash \; left\; (\backslash \; ln\; \backslash \; left\; (\{\backslash \; dfrac\; \{z\}\; \{2\}\}\; \backslash \; right)\; +\; \backslash \; gamma\; \backslash \; right)\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha\; =\; 0\; \backslash \backslash \; -\; \{\backslash \; dfrac\; \{\backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; pi\}\}\; \backslash \; left\; (\{\backslash \; dfrac\; \{2\}\; \{z\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; +\; \{\backslash \; dfrac\; \{1\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\; \}\}\; \backslash \; left\; (\{\backslash \; dfrac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \backslash \; cot\; (\backslash \; alpha\; \backslash \; pi)\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha\; \{\backslash \; text\; \{не\; является\; неположительным\; целым\; числом\; (один\; член\; доминирует,\; если\}\}\; \backslash \; alpha\; \{\backslash \; text\; \{не\; является\; воображаемым)\}\},\; \backslash \backslash \; -\; \{\backslash \; dfrac\; \{(-1)\; ^\; \{\backslash \; alpha\}\; \backslash \; Gamma\; (-\; \backslash \; alpha)\}\; \{\backslash \; pi\}\}\; \backslash \; left\; (\{\backslash \; dfrac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha\; \{\backslash \; text\; \{\; -\; отрицательное\; целое\; число,\}\}\; \backslash \; end\; \{cases\}\}\}$

где γ - константа Эйлера - Маскерони (0,5772...).

Для больших вещественных аргументов z ≫ | α - 1/4 | нельзя записать истинную асимптотику для функций Бесселя и второго рода (если α не является полуцелым числом ), потому что они имеют нули до бесконечности, что должно было бы точно соответствовать любому асимптотическому разложению. Однако для данного значения arg z можно написать уравнение, содержащее член порядка | z |:

(При α = 1/2 члены в этих формулах полностью выпадают; см. Сферические функции Бесселя выше.) Даже если эти уравнения верны, для комплексного z могут быть доступны лучшие приближения. Например, J 0 (z), когда z находится рядом с отрицательной действительной линией, лучше аппроксимируется

$J\; 0\; (z)\; \approx \; -\; 2\; \pi \; z\; cos\; \; (z\; +\; \pi \; 4)\; \{\backslash \; displaystyle\; J\_\; \{0\}\; (z)\; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{-2\}\; \{\backslash \; pi\; z\}\}\}\; \backslash \; cos\; \backslash \; left\; (z\; +\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{4\}\}\; \backslash \; right)\}$

чем на

$J\; 0\; (z)\; \approx \; 2\; \pi \; z\; cos\; \; (z\; -\; \pi \; 4).\; \{\backslash \; displaystyle\; J\_\; \{0\}\; (z)\; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\; z\}\}\}\; \backslash \; cos\; \backslash \; left\; (z\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{4\}\}\; \backslash \; right).\; \}$

Асимптотики для функций Ганкеля:

Их можно распространить на другие значения arg z с использованием уравнения, связывающих H. α(ze) и H. α(ze) с H. α(z) и H. α(z).

Интересно, что хотя функция Бесселя первого - это среднее значение двух функций Ганкеля, J α (z) не является асимптотическим средним средним этих двух асимптотических форм, когда z отрицательно (потому что одна или другая функция) другая не будет там будет правильно, в зависимости от используемого arg z). Но асимптотики для функций Ганкеля позволяют нам записывать асимптотики для функций Бесселя первого и второго рода для комплексных (не действующих) z, пока | z | стремится к бесконечности при постоянном фазовом угле arg z (с использованием квадратного корня с положительной действительной частью):

Для модифицированных функций Бесселя Ханкель разработал также асимптотические разложения (с большим аргументом) :

Когда α = 1/2, все члены, кроме первого, обращаются в нуль, и мы имеем

Для малых аргументов 0 < |z| ≪ √α + 1, we have

$I\; \alpha \; (z)\; \sim \; 1\; \Gamma \; (\alpha \; +\; 1)\; (z\; 2)\; \alpha ,\; K\; \alpha \; (z)\; \sim \; \{-\; ln\; \; (z\; 2)\; -\; \gamma ,\; если\; \alpha \; =\; 0\; \Gamma \; (\alpha )\; 2\; (2\; z)\; \alpha ,\; если\; \alpha >0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; I\; \_\; \{\backslash \; alpha\}\; (z)\; \backslash \; sim\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\},\; \backslash \backslash \; K\; \_\; \{\backslash \; alpha\}\; (z)\; \backslash \; sim\; \{\backslash \; begin\; \{cases\}\; -\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; dfrac\; \{z\}\; \{2\}\}\; \backslash \; right)\; -\; \backslash \; gamma\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha\; =\; 0\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; Gamma\; (\backslash \; alpha)\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; dfrac\; \{2\; \}\; \{z\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>0\; \backslash \; end\; \{cases\}\}\; \backslash \; end\; \{align\}\}\}$

Приближение полной области с элементарными функциями

Очень хорошее приближение (ошибка ниже $0,3\%\; \{\backslash \; displaystyle\; 0.3\; \backslash \%\}$максимального значения 1) функции Бесселя $J\; 0\; \{\backslash \; displaystyle\; J\_\; \{0\}\}$для произвольного значения аргумента x может быть получено с помощью элементарных функций путем объединения тригонометрическое приближение, работающее для меньших значений x с выражением, содержащим функцию ослабленного косинуса, действительную для больших аргументов с использованием функции плавного перехода $1\; 1\; +\; (x\; /\; 7)\; 20\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{1\}\; +\; (x\; /\; 7)\; ^\; \{20\}\}\}\}$т.е.

$J\; 0\; (x)\; \approx \; [1\; 6\; +\; 1\; 3\; cos\; \; x\; 2\; +\; 1\; 3\; cos\; \; 3\; x\; 2\; +\; 1\; 6\; cos\; \; x]\; 1\; 1\; +\; (x\; /\; 7)\; 20\; +\; 2\; \pi \; |\; х\; |\; cos\; \; [x\; -\; \pi \; 4\; sign\; \; (x)]\; [1\; -\; 1\; 1\; +\; (x\; /\; 7)\; 20].\; \{\backslash \; displaystyle\; J\_\; \{0\}\; (x)\; \backslash \; приблизительно\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{6\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; cos\; \{\backslash \; frac\; \{x\}\; \{2\}\}\; +\; \{\; \backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; cos\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{3\}\}\; x\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; \backslash \; cos\; x\; \backslash \; right]\; \{\backslash \; frac\; \{1\; \}\; \{1+\; (x\; /\; 7)\; ^\; \{20\}\}\}\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\; |\; x\; |\}\}\}\; \backslash \; cos\; \backslash \; left\; [x\; -\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{4\; \}\}\; \backslash \; operatorname\; \{sgn\}\; (x)\; \backslash \; right]\; \backslash \; left\; [1\; -\; \{\backslash \; frac\; \{1\}\; \{1+\; (x\; /\; 7)\; ^\; \{20\}\}\}\; \backslash \; right].\}$

Свойства

Для целочисленного порядка α = n, J n часто определяется через ряд Лорана для производящей функции:

$e\; (x\; 2)\; (t\; -\; 1\; t)\; Знак\; равно\; \sum \; N\; =\; -\; \infty \; \infty \; J\; N\; (x)\; tn\; \{\backslash \; displaystyle\; e\; ^\; \{\backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; \backslash \; left\; (t\; -\; \{\backslash \; frac\; \{1\}\; \{t\}\})\; \backslash \; right)\}\; =\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; J\_\; \{n\}\; (x)\; t\; ^\; \{n\}\}$

подход, используемый P. А. Хансен в 1843 году. (Это можно обобщить на нецелочисленный порядок с помощью контурного интегрирования или других методов.) Еще одним важным соотношением для целочисленных порядков является разложение Якоби – Ангера :

$eiz\; соз\; \; \varphi \; =\; \sum \; N\; =\; -\; \infty \; \infty \; в\; J\; N\; (z)\; ein\; \varphi \; \{\backslash \; displaystyle\; e\; ^\; \{iz\; \backslash \; cos\; \backslash \; phi\}\; =\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; i\; ^\; \{n\}\; J\_\; \{n\}\; (z)\; e\; ^\; \{in\; \backslash \; phi\}\}$

и

$e\; \pm \; iz\; sin\; \; \varphi \; =\; J\; 0\; (z)\; +\; 2\; \sum \; n\; =\; 1\; \infty \; J\; 2\; n\; (z)\; cos\; \; (2\; n\; \varphi )\; \pm \; 2\; i\; \sum \; n\; =\; 0\; \infty \; J\; 2\; n\; +\; 1\; (z)\; sin\; \; ((2\; n\; +\; 1)\; \varphi )\; \{\backslash \; displayst\; yle\; e\; ^\; \{\backslash \; pm\; iz\; \backslash \; sin\; \backslash \; phi\}\; =\; J\_\; \{0\}\; (z)\; +2\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; J\_\; \{2n\}\; (z)\; \backslash \; cos\; (2n\; \backslash \; phi)\; \backslash \; pm\; 2i\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; J\_\; \{2n\; +\; 1\}\; (z)\; \backslash \; sin\; ((2n\; +\; 1)\; \backslash \; phi)\}$

, который используется для расширения плоской волны как суммы цилиндрических волн, или найти ряд Фурье тонально-модулированного сигнала FM.

В более общем смысле, ряд

$f\; (z)\; =\; a\; 0\; \nu \; J\; \nu \; (z)\; +\; 2\; \cdot \; \sum \; k\; =\; 1\; \infty \; ak\; \nu \; J\; \nu \; +\; k\; (z)\; \{\backslash \; displaystyle\; f\; (z)\; =\; a\_\; \{0\}\; ^\; \{\backslash \; nu\}\; J\; \_\; \{\backslash \; nu\}\; (z)\; +2\; \backslash \; cdot\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; a\_\; \{k\}\; ^\; \{\backslash \; nu\}\; J\; \_\; \{\backslash \; nu\; +\; k\}\; (z)\}$

называется разложением Неймана функции f. Коэффициенты при ν = 0 имеют явный вид

$a\; k\; 0\; =\; 1\; 2\; \pi \; i\; \int \; |\; z\; |\; знак\; равно\; cf\; (z)\; О\; К\; (z)\; dz\; \{\backslash \; displaystyle\; a\_\; \{k\}\; ^\; \{0\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; int\; \_\; \{|\; z\; |\; =\; c\}\; f\; (z)\; O\_\; \{k\}\; (z)\; \backslash ,\; dz\}$

где O k - многочлен Неймана.

Выбранные функции допускают специальное представление

$f\; (z)\; =\; \sum \; k\; =\; 0\; \infty \; ak\; \nu \; J\; \nu \; +\; 2\; K\; (z)\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; a\_\; \{k\}\; ^\; \{\backslash \; nu\}\; J\; \_\; \{\backslash \; nu\; +\; 2k\}\; (z)\}$

с

$ak\; \nu \; =\; 2\; (\nu \; +\; 2\; k)\; \int \; 0\; \infty \; f\; (z)\; J\; \nu \; +\; 2\; k\; (z)\; zdz\; \{\backslash \; displaystyle\; a\_\; \{k\}\; ^\; \{\backslash \; nu\}\; =\; 2\; (\; \backslash \; nu\; +\; 2k)\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; f\; (z)\; \{\backslash \; frac\; \{J\; \_\; \{\backslash \; nu\; +\; 2k\}\; (z)\}\; \{z\}\}\; \backslash ,\; dz\}$

из-за ортогональности отношение

$\int \; 0\; \infty \; J\; \alpha \; (z)\; J\; \beta \; (z)\; dzz\; =\; 2\; \pi \; sin\; \; (\pi \; 2\; (\alpha \; -\; \beta ))\; \alpha \; 2\; -\; \beta \; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\; \}\; J\; \_\; \{\backslash \; alpha\}\; (z)\; J\; \_\; \{\backslash \; beta\}\; (z)\; \{\backslash \; frac\; \{dz\}\; \{z\}\}\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\; \{\backslash \; frac\; \{\backslash \; sin\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; (\backslash \; alpha\; -\; \backslash \; beta)\; \backslash \; right)\}\; \{\backslash \; alpha\; ^\; \{2\}\; -\; \backslash \; beta\; ^\; \{2\}\}\}\}$

В общем, если f имеет точку ветвления около начала координат такой природы, что

$f\; (z)\; =\; \sum \; k\; =\; 0\; ak\; J\; \nu \; +\; k\; (z)\; \{\backslash \; displaystyle\; f\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; a\_\; \{k\}\; J\_\; \{\; \backslash \; nu\; +\; k\}\; (z)\}$

, тогда

$L\; \{\sum \; k\; =\; 0\; ak\; J\; \nu \; +\; к\}\; (s)\; знак\; равно\; 1\; 1\; +\; s\; 2\; \sum \; К\; знак\; равно\; 0\; ак\; (s\; +\; 1\; +\; s\; 2)\; \nu \; +\; к\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; left\; \backslash \; \{\backslash \; sum\; \_\; \{k\; =\; 0\}\; a\_\; \{k\}\; J\; \_\; \{\backslash \; nu\; +\; k\}\; \backslash \; right\; \backslash \}\; (s)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; +\; s\; ^\; \{2\}\}\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; \{\backslash \; frac\; \{\; a\_\; \{k\}\}\; \{\backslash \; left\; (s\; +\; \{\backslash \; sqrt\; \{1\; +\; s\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; nu\; +\; k\}\}\}\}$

или

$\sum \; k\; =\; 0\; ak\; \xi \; \nu \; +\; К\; знак\; равно\; 1\; +\; \xi \; 2\; 2\; \xi \; L\; \{е\}\; (1\; -\; \xi \; 2\; 2\; \xi )\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; a\_\; \{k\}\; \backslash \; xi\; ^\; \{\backslash \; nu\; +\; k\}\; =\; \{\backslash \; frac\; \{\; 1+\; \backslash \; xi\; ^\; \{2\}\}\; \{2\; \backslash \; xi\}\}\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; \{f\; \backslash \}\; \backslash \; left\; (\{\backslash \; frac\; \{1-\; \backslash \; xi\; ^\; \{2\}\}\; \{2\; \backslash \; xi\}\}\; \backslash \; right)\}$

где $L\; \{f\}\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; \{f\; \backslash \}\}$- это преобразование Лапласа для f.

Другой способ определения функций Бесселя - это метод Пуассона формула представления и формула Мелера-Сонина:

$J\; \nu \; (z)\; =\; (z\; 2)\; \nu \; \Gamma \; (\nu \; +\; 1\; 2)\; \pi \; \int \; -\; 1\; 1\; eizs\; (1\; -\; s\; 2)\; \nu \; -\; 1\; 2\; ds\; =\; 2\; (z\; 2)\; \nu \; \cdot \; \pi \; \cdot \; \Gamma \; (1\; 2\; -\; \nu )\; \int \; 1\; \infty \; sin\; \; zu\; (u\; 2\; -\; 1)\; \nu \; +\; 1\; 2\; du\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; J\; \_\; \{\backslash \; nu\}\; (z)\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; nu\}\}\; \{\backslash \; Gamma\; \backslash \; left\; (\backslash \; nu\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\}\}\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; e\; ^\; \{izs\}\; \backslash \; left\; (1-s\; ^\; \{2\}\; \backslash \; справа)\; ^\; \{\backslash \; nu\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash ,\; ds\; \backslash \backslash \; [5px]\; =\; \{\backslash \; frac\; \{2\}\; \{\{\backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\}\; ^\; \{\backslash \; nu\}\; \backslash \; cdot\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\; \backslash \; cdot\; \backslash \; Gamma\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \backslash \; nu\; \backslash \; right)\}\}\; \backslash \; int\; \_\; \{1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; sin\; zu\}\; \{\backslash \; left\; (u\; ^\; \{2\}\; -1\; \backslash \; right)\; ^\; \{\backslash \; nu\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}\}\; \backslash ,\; du\; \backslash \; end\; \{\; align\}\}\}$

где ν>−1/2 и z ∈ C . Эта формула особенно полезна при работе с преобразованием Фурье.

уравнение Бесселя становится эрмитовым (самосопряженным), если оно делится на x, решения должны удовлетворять ортогональности для соответствующих граничных условий. В частности, отсюда следует, что:

$\int \; 0\; 1\; x\; J\; \alpha \; (xu\; \alpha ,\; m)\; J\; \alpha \; (xu\; \alpha ,\; n)\; dx\; =\; \delta \; m,\; n\; 2\; [J\; \alpha \; +\; 1\; (u\; \alpha ,\; m)]\; 2\; знака\; равно\; \delta \; м,\; N\; 2\; [J\; \alpha \; \prime \; (u\; \alpha ,\; m)]\; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; xJ\; \_\; \{\backslash \; alpha\}\; \backslash \; left\; (xu\; \_\; \{\backslash \; alpha,\; m\}\; \backslash \; right)\; J\_\; \{\backslash \; alpha\}\; \backslash \; left\; (xu\; \_\; \{\backslash \; alpha,\; n\}\; \backslash \; right)\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{\backslash \; delta\; \_\; \{m,\; n\}\}\; \{2\}\}\; \backslash \; left\; [J\; \_\; \{\backslash \; альфа\; +1\}\; \backslash \; left\; (u\; \_\; \{\backslash \; alpha,\; m\}\; \backslash \; right)\; \backslash \; right]\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{\backslash \; delta\; \_\; \{m,\; n\}\}\; \{2\}\}\; \backslash \; left\; [J\; \_\; \{\backslash \; alpha\}\; \text{'}\backslash \; left\; (u\_\; \{\backslash \; alpha,\; m\}\; \backslash \; right)\; \backslash \; right]\; ^\; \{2\}\}$

где α>−1, δ m, n - дельта Кронекера, а u α, m - m-й ноль из J α (x). Это соотношение ортогональности можно использовать для извлечения коэффициентов в рядх Фурье - Бесселя, где функция раскрывается в базисе функций J α (xu α, m) для фиксированного α и переменного м.

Аналогичное соотношение для сферических функций Бесселя следует немедленно:

$\int \; 0\; 1\; x\; 2\; j\; \alpha \; (xu\; \alpha ,\; m)\; j\; \alpha \; (xu\; \alpha ,\; n)\; dx\; =\; \delta \; m,\; n\; 2\; [j\; \alpha \; +\; 1\; (U\; \alpha ,\; м)]\; 2\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; x\; ^\; \{2\}\; j\; \_\; \{\backslash \; alpha\}\; \backslash \; left\; (xu\; \_\; \{\backslash \; alpha,\; m\}\; \backslash \; right)\; j\; \_\; \{\; \backslash \; alpha\}\; \backslash \; left\; (xu\; \_\; \{\backslash \; alpha,\; n\}\; \backslash \; right)\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{\backslash \; delta\; \_\; \{m,\; n\}\}\; \{2\}\}\; \backslash \; left\; [j\; \_\; \{\backslash \; alpha\; +1\}\; \backslash \; left\; (u\_\; \{\backslash \; alpha,\; m\}\; \backslash \; right)\; \backslash \; right]\; ^\; \{2\}\}$

Если определить функцию товарного вагона x, которая зависит от малого параметра ε, как:

$f\; \epsilon \; (Икс)\; знак\; равно\; \epsilon \; rect\; \; (Икс\; -\; 1\; \epsilon )\; \{\backslash \; Displaystyle\; f\; \_\; \{\backslash \; varepsilon\}\; (x)\; =\; \backslash \; varepsilon\; \backslash \; OperatorName\; \{rect\}\; \backslash \; left\; (\{\backslash \; frac\; \{x-1\}\; \{\backslash \; varepsilon\}\}\; \backslash \; right)\}$

(где rect - это функция прямоугольника ), затем его преобразование Ханкеля (любого заданного порядка α>−1/2), g ε (k) приближается к J α (k), когда ε приближается к нулю для любого заданного k. И наоборот, преобразование Ханкеля (того же порядка) для g ε (k) есть f ε (x):

$\int \; 0\; \infty \; k\; J\; \alpha \; (kx)\; g\; \epsilon \; (к)\; dk\; знак\; равно\; е\; \epsilon \; (Икс)\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; kJ\; \_\; \{\backslash \; alpha\}\; (kx)\; g\; \_\; \{\backslash \; varepsilon\}\; (k)\; \backslash ,\; dk\; =\; f\; \_\; \{\backslash \; varepsilon\}\; (\; x)\}$

который равен нулю везде, кроме около 1. Когда ε приближается к нулю, правая часть приближается к δ (x - 1), где δ - дельта-функция Дирака. Это допускает предел (в распределительном смысле):

$\int \; 0\; \infty \; k\; J\; \alpha \; (kx)\; J\; \alpha \; (k)\; dk\; =\; \delta \; (x\; -\; 1)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\; \}\; ^\; \{\backslash \; infty\}\; kJ\; \_\; \{\backslash \; alpha\}\; (kx)\; J\; \_\; \{\backslash \; alpha\}\; (k)\; \backslash ,\; dk\; =\; \backslash \; delta\; (x-1)\}$

После замены переменных получается уравнение замыкания:

$\int \; 0\; \infty \; Икс\; J\; \alpha \; (ux)\; J\; \alpha \; (vx)\; dx\; знак\; равно\; 1\; u\; \delta \; (u\; -\; v)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; xJ\; \_\; \{\backslash \; alpha\}\; (ux)\; J\; \_\; \{\backslash \; alpha\; \}\; (vx)\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{1\}\; \{u\}\}\; \backslash \; delta\; (uv)\}$

для α>−1/2. Преобразование Ханкеля может выразить довольно произвольную функцию как интеграл от функций Бесселя разного масштаба. Для сферических функций Бесселя соотношение ортогональности:

$\int \; 0\; \infty \; x\; 2\; j\; \alpha \; (ux)\; j\; \alpha \; (vx)\; dx\; =\; \pi \; 2\; u\; 2\; \delta \; (u\; -\; v)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; x\; ^\; \{2\}\; j\; \_\; \{\backslash \; alpha\}\; (ux)\; j\; \_\; \{\backslash \; alpha\}\; (vx)\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2u\; ^\; \{2\}\}\}\; \backslash \; delta\; (uv)\}$

для α>−1.

Другое важное свойство уравнений Бесселя, которое следует из тождества Абеля, включает вронскиан решений:

$A\; \alpha \; (x)\; d\; B\; \alpha \; dx\; -\; d\; A\; \alpha \; dx\; В\; \alpha \; (Икс)\; знак\; равно\; С\; \alpha \; Икс\; \{\backslash \; Displaystyle\; A\; \_\; \{\backslash \; alpha\}\; (x)\; \{\backslash \; frac\; \{dB\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; -\; \{\backslash \; frac\; \{dA\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; B\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{C\; \_\; \{\backslash \; alpha\}\}\; \{x\}\}\}$

где A α и B α - любые два решения уравнения Бесселя, и C α является константой, не зависящей от x (которая зависит от α и от конкретных рассматриваемых функций Бесселя). В частности,

$J\; \alpha \; (x)\; d\; Y\; \alpha \; dx\; -\; d\; J\; \alpha \; dx\; Y\; \alpha \; (x)\; =\; 2\; \pi \; x\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (x)\; \{\backslash \; frac\; \{dY\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; -\; \{\backslash \; frac\; \{dJ\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; Y\; \_\; \{\backslash \; alpha\}\; (x)\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\; x\}\}\}$

и

$I\; \alpha \; (Икс)\; d\; К\; \alpha \; dx\; -\; d\; я\; \alpha \; dx\; К\; \alpha \; (Икс)\; =\; -\; 1\; Икс,\; \{\backslash \; Displaystyle\; I\; \_\; \{\backslash \; alpha\}\; (x)\; \{\backslash \; гидроразрыва\; \{dK\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; -\; \{\backslash \; frac\; \{dI\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\}\; K\; \_\; \{\backslash \; alpha\}\; (x)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{x\}\},\}$

для α>−1.

При α>−1 четная целая функция рода 1, xJ α (x), имеет только действительные нули. Пусть

- все его положительные нули, тогда

$J\; \alpha \; (z)\; =\; (z\; 2)\; \alpha \; \Gamma \; (\alpha \; +\; 1)\; \prod \; n\; =\; 1\; \infty \; (1\; -\; z\; 2\; j\; \alpha ,\; n\; 2)\; \{\backslash \; displaystyle\; J\; \_\; \{\backslash \; alpha\}\; (z)\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\}\; \{\backslash \; Gamma\; (\backslash \; alpha\; +1)\}\}\; \backslash \; prod\; \_\; \{\; n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{j\; \_\; \{\backslash \; alpha,\; n\}\; ^\; \{2\}\}\}\; \backslash \; right)\}$

(Есть большой число других известных интегралов и тождеств, которые здесь не воспроизводятся, но которые можно найти в справочных материалах.)

Повторяющиеся отношения

Функции J α, Y α, H. αи H. αудовлетворяют рекуррентным соотношениям

$2\; \alpha \; x\; Z\; \alpha \; (x)\; =\; Z\; \alpha \; -\; 1\; (x)\; +\; Z\; \alpha \; +\; 1\; (\; х)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{2\; \backslash \; alpha\}\; \{x\}\}\; Z\; \_\; \{\backslash \; alpha\}\; (x)\; =\; Z\; \_\; \{\backslash \; alpha\; -1\}\; (x)\; +\; Z\; \_\; \{\backslash \; alpha\; +1\}\; (x)\}$

и

$2\; d\; Z\; \alpha \; (x)\; dx\; =\; Z\; \alpha \; -\; 1\; (x)\; -\; Z\; \alpha \; +\; 1\; (x),\; \{\backslash \; displaystyle\; 2\; \{\backslash \; frac\; \{dZ\; \_\; \{\backslash \; alpha\}\; (x)\}\; \{dx\}\; \}\; =\; Z\; \_\; \{\backslash \; alpha\; -1\}\; (x)\; -Z\; \_\; \{\backslash \; alpha\; +1\}\; (x),\}$

. где Z обозначает J, Y, H или H. Эти две идентичности часто комбинируются, например добавлены или вычтены, чтобы получить различные другие отношения. Таким образом, например, можно вычислить функции Бесселя более высоких порядков (или более высокие производные) с учетом значений более низких порядков (или более низких производных). В частности, следует, что

$(1\; xddx)\; m\; [x\; \alpha \; Z\; \alpha \; (x)]\; =\; x\; \alpha \; -\; m\; Z\; \alpha \; -\; m\; (x),\; (1\; xddx)\; m\; [Z\; \alpha \; (x)\; x\; \alpha ]\; =\; (-\; 1)\; м\; Z\; \alpha \; +\; м\; (х)\; х\; \alpha \; +\; м.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; frac\; \{d\}\; \{dx\}\}\; \backslash \; right)\; ^\; \{m\}\; \backslash \; left\; [x\; ^\; \{\backslash \; alpha\}\; Z\_\; \{\; \backslash \; alpha\}\; (x)\; \backslash \; right]\; =\; x\; ^\; \{\backslash \; alpha\; -m\}\; Z\; \_\; \{\backslash \; alpha\; -m\}\; (x),\; \backslash \backslash \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{x\}\}\; \{\backslash \; frac\; \{d\; \}\; \{dx\}\}\; \backslash \; right)\; ^\; \{m\}\; \backslash \; left\; [\{\backslash \; frac\; \{Z\; \_\; \{\backslash \; alpha\}\; (x)\}\; \{x\; ^\; \{\backslash \; alpha\}\}\}\; \backslash \; right]\; =\; (-\; 1)\; ^\; \{m\}\; \{\backslash \; frac\; \{Z\; \_\; \{\backslash \; alpha\; +\; m\}\; (x)\}\; \{x\; ^\; \{\backslash \; alpha\; +\; m\}\}\}.\; \backslash \; end\; \{align\}\}\}$

Модифицированные функции Бесселя подчиняются аналогичным отношениям:

$e\; (x\; 2)\; (T\; +\; 1\; T)\; знак\; равно\; \sum \; N\; =\; -\; \infty \; \infty \; I\; N\; (x)\; tn\; \{\backslash \; displaystyle\; e\; ^\; \{\backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{2\}\}\; \backslash \; right)\; \backslash \; left\; (t\; +\; \{\backslash \; frac\; \{1\}\; \{t\}\}\; \backslash \; right)\}\; =\; \backslash \; sum\; \_\; \{n\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; I\_\; \{n\}\; (x)\; t\; ^\; \{n\}\}$

и

$ez\; cos\; \; \theta \; знак\; равно\; I\; 0\; (z)\; +\; 2\; \sum \; n\; знак\; равно\; 1\; \infty \; I\; n\; (z)\; cos\; \; n\; \theta .\; \{\backslash \; displaystyle\; e\; ^\; \{z\; \backslash \; cos\; \backslash \; theta\}\; =\; I\_\; \{0\}\; (z)\; +2\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; I\_\; \{n\}\; (z)\; \backslash \; cos\; n\; \backslash \; theta.\}$

и

$1\; 2\; \pi \; \int \; 0\; 2\; \pi \; ez\; cos\; \; (m\; \theta )\; +\; y\; cos\; \; \theta \; =\; I\; 0\; (z)\; I\; 0\; (y)\; +\; 2\; \sum \; n\; =\; 1\; \infty \; I\; n\; (z)\; I\; mn\; (у).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{2\; \backslash \; pi\}\; e\; ^\; \{z\; \backslash \; cos\; (m\; \backslash \; theta)\; +\; y\; \backslash \; cos\; \backslash \; theta\}\; =\; I\_\; \{0\}\; (z)\; I\_\; \{0\}\; (y)\; +2\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; I\_\; \{n\}\; (z)\; I\_\; \{mn\}\; (y).\}$

. Рекуррентное соотношение имеет вид

$C\; \alpha \; -\; 1\; (x)\; -\; C\; \alpha \; +\; 1\; (x)\; =\; 2\; \alpha \; x\; C\; \alpha \; (x),\; C\; \alpha \; -\; 1\; (x)\; +\; C\; \alpha \; +\; 1\; (x)\; =\; 2\; d\; C\; \alpha \; dx,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; C\; \_\; \{\backslash \; alpha\; -1\}\; (x)\; -C\; \_\; \{\backslash \; alpha\; +1\}\; (x)\; =\; \{\backslash \; frac\; \{2\; \backslash \; alpha\}\; \{x\}\}\; C\; \_\; \{\backslash \; alpha\}\; (x),\; \backslash \backslash \; C\; \_\; \{\backslash \; alpha\; -1\}\; (x)\; +\; C\; \_\; \{\backslash \; alpha\; +1\}\; (x)\; =\; 2\; \{\backslash \; frac\; \{dC\; \_\; \{\backslash \; alpha\}\}\; \{dx\}\},\; \backslash \; end\; \{align\}\}\}$

, где C α обозначает I α или eK α. Эти рекуррентные соотношения полезны для задач дискретной диффузии.

Функции Бесселя подчиняются теореме умножения

$\lambda \; -\; \nu \; J\; \nu \; (\lambda \; z)\; =\; \sum \; n\; =\; 0\; \infty \; 1\; n!\; ((1\; -\; \lambda \; 2)\; Z\; 2)\; N\; J\; \nu \; +\; N\; (Z),\; \{\backslash \; Displaystyle\; \backslash \; lambda\; ^\; \{-\; \backslash \; nu\}\; J\; \_\; \{\backslash \; nu\}\; (\backslash \; lambda\; z)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{n!\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; left\; (1-\; \backslash \; lambda\; ^\; \{2\}\; \backslash \; right)\; z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{n\}\; J\_\; \{\backslash \; nu\; +\; n\}\; (z),\}$

где λ и ν могут быть взяты как произвольные комплексные числа. Для | λ - 1 | < 1, the above expression also holds if J is replaced by Y. The analogous identities for modified Bessel functions and |λ − 1| < 1 are

$\lambda \; -\; \nu \; I\; \nu \; (\lambda \; z)\; знак\; равно\; \sum \; n\; =\; 0\; \infty \; 1\; n!\; ((\lambda \; 2\; -\; 1)\; z\; 2)\; N\; я\; \nu \; +\; N\; (z)\; \{\backslash \; Displaystyle\; \backslash \; lambda\; ^\; \{-\; \backslash \; nu\}\; I\; \_\; \{\backslash \; nu\}\; (\backslash \; lambda\; z)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\; \backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{n!\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; left\; (\backslash \; lambda\; ^\; \{2\}\; -1\; \backslash \; right)\; z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{n\}\; I\_\; \{\; \backslash \; nu\; +\; n\}\; (z)\}$

и

$\lambda \; -\; \nu \; K\; \nu \; (\lambda \; z)\; =\; \sum \; n\; =\; 0\; \infty \; (-\; 1)\; nn!\; ((\lambda \; 2\; -\; 1)\; z\; 2)\; n\; K\; \nu \; +\; n\; (z).\; \{\backslash \; displaystyle\; \backslash \; lambda\; ^\; \{-\; \backslash \; nu\}\; K\; \_\; \{\backslash \; nu\}\; (\backslash \; lambda\; z)\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{n\; !\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; left\; (\backslash \; lambda\; ^\; \{2\}\; -1\; \backslash \; right)\; z\}\; \{2\}\}\; \backslash \; right)\; ^\; \{n\}\; K\; \_\; \{\backslash \; nu\; +\; n\}\; (z).\}$

Гипотеза Бурже

Сам Бессель первоначально доказал, что для неотрицательных целых чисел n уравнение J n (x) = 0 имеет бесконечное число решений по x. Однако, когда функции J n (x) нанесены на один и тот же график, кажется, что ни один из нулей не совпадает для разных значений n, за исключением нуля при x = 0. Это явление известно как Гипотеза Бурже в честь французского математика XIX века, изучавшего функции Бесселя. В частности, он заявляет, что для любых целых чисел n ≥ 0 и m ≥ 1 функции J n (x) и J n + m (x) не имеют общих нулей, кроме одного при x = 0. Гипотеза была доказана Карлом Людвигом Сигелем в 1929 году.

Численные подходы

Для численных исследований нулей функции Бесселя см. Gil, Segura Temme (2007) ошибка harvtxt: нет цели: CITEREFGilSeguraTemme2007 (help ), Kravanja et al. (1998) ошибка harvtxt: нет цели: CITEREFKravanjaRagosVrahatisZafiropoulos1998 (help ) и Moler (2004) ошибка harvtxt: нет цели: CITEREFMoler2004 (help ).

• Функция Гнева
• Функция Бесселя – Клиффорда
• Функция Бесселя – Мейтланда
• Многочлены Бесселя
• Ряд Фурье – Бесселя
• Ряд Шлёмильха
• Хан-Экстон q-функция Бесселя
• преобразование Ханкеля
• функция Джексона q-Бесселя
• функции Кельвина
• преобразование Конторовича-Лебедева
• правило сумм Лерша – Ньюбергера
• функция Ломмеля
• многочлен Ломмеля
• Многочлен Неймана
• Сониновая формула
• Функция Струве
• Колебания кругового барабана
• Функция Вебера