 . Инволюционная симметрия. Cs, (*). [] = . Инволюционная симметрия. Cs, (*). [] = |  . Циклический симметрия. Cnv, (* nn). [n] = . Циклический симметрия. Cnv, (* nn). [n] = |  . Двугранная симметрия. Dnh, (* n22). [n, 2] = . Двугранная симметрия. Dnh, (* n22). [n, 2] = | |
| Группа полиэдров, [n, 3], (* n32) | |||
|---|---|---|---|
 . Тетраэдрическая симметрия. Td, (* 332). [3,3] = . Тетраэдрическая симметрия. Td, (* 332). [3,3] = |  . Октаэдрическая симметрия. Oh, (* 432). [4,3] = . Октаэдрическая симметрия. Oh, (* 432). [4,3] = |  . Икосаэдрическая симметрия. Ih, (* 532). [5,3] = . Икосаэдрическая симметрия. Ih, (* 532). [5,3] = | |
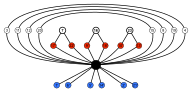
 График цикла. Четыре шестиугольных цикла имеют общую инверсию (черный узел наверху). Шестиугольники симметричны, поэтому, например, 3 и 4 находятся в одном цикле.
График цикла. Четыре шестиугольных цикла имеют общую инверсию (черный узел наверху). Шестиугольники симметричны, поэтому, например, 3 и 4 находятся в одном цикле. Правильный октаэдр имеет 24 симметрии вращения (или сохраняющие ориентацию) и 48 симметрий в целом. К ним относятся преобразования, сочетающие отражение и вращение. Куб имеет тот же набор симметрий, поскольку это многогранник, двойственный октаэдру.
Группа сохраняющих ориентацию симметрий - это S 4, симметрическая группа или группа перестановок четырех объектов, поскольку существует ровно одна такая симметрия для каждого перестановка четырех пар противоположных граней октаэдра.
Хиральные и полная (или ахиральная ) октаэдрическая симметрия - это дискретные точечные симметрии (или, эквивалентно, симметрии на сфера ) с наибольшими группами симметрии , совместимыми с трансляционной симметрией. Они входят в число кристаллографических точечных групп кубической кристаллической системы.
| Элементы O | Инверсии элементов O | ||
|---|---|---|---|
| идентичности | 0 | инверсия | 0' |
| 3 × поворот на 180 ° вокруг оси 4-го порядка | 7, 16, 23 | 3-кратное отражение в плоскости, перпендикулярной оси 4-го порядка | 7 ', 16', 23 ' |
| 8-кратное вращение на 120 ° вокруг оси 3-го порядка | 3, 4, 8, 11, 12, 15, 19, 20 | 8-кратное вращение на 60 ° | 3 ', 4', 8 ', 11', 12 ', 15', 19 ', 20' |
| 6-кратное вращение на 180 ° вокруг двукратной оси | 1 ', 2', 5 ', 6', 14 ', 21' | 6-кратное отражение в плоскости, перпендикулярной двукратной оси | 1, 2, 5, 6, 14, 21 |
| 6-кратное вращение на 90 ° вокруг 4-кратной оси | 9 ', 10', 13 ', 17', 18 ', 22' | 6-кратное вращение на 90 ° | 9, 10, 13, 17, 18, 22 |
| Примеры | ||||
|---|---|---|---|---|
 . .  |  . .  |  . .  |  . .  |  . .  |
 . .  |  . .  |  . .  |  . .  |  . .  |
| Полный список можно найти в статье Викиверситета. | ||||
Поскольку гипероктаэдрическая группа размерности 3, полная октаэдрическая группа является сплетением 






Так, например, тождество 







A rotoreflection - это комбинация вращения и отражения.
| Иллюстрация кругового отражения | ||||
|---|---|---|---|---|
 Отражение Отражение   , примененное к повороту на 120 ° , примененное к повороту на 120 °   , дает поворот на 60 ° , дает поворот на 60 °  . .. | ||||
 Отражение Отражение   примененный к повороту на 90 ° примененный к повороту на 90 °   дает угол поворота на 90 ° дает угол поворота на 90 °  . .. | ||||
| Гирационные оси | ||
|---|---|---|
| C4. | C3. | C2. |
| 3 | 4 | 6 |
O, 432, или [4,3] порядка 24, являются хиральной октаэдрической симметрией или вращательной октаэдрическая симметрия . Эта группа похожа на хиральную тетраэдрическую симметрию T, но оси C 2 теперь являются осями C 4, и, кроме того, имеется 6 C 2 оси через середины граней куба. T d и O изоморфны как абстрактные группы: они оба соответствуют S 4, симметричной группе на 4 объектах. T d - это объединение T и набора, полученного путем объединения каждого элемента O \ T с инверсией. O - группа вращения куба и правильного октаэдра.
| Ортогональная проекция | Стереографическая проекция | ||
|---|---|---|---|
| 2-кратная | 4-кратное | 3-кратное | 2-кратное |
 |  |  |  |
Oh, * 432, [4,3] или м3 · м порядка 48 - ахиральная октаэдрическая симметрия или полная октаэдрическая симметрия . Эта группа имеет те же оси вращения, что и O, но с зеркальными плоскостями, содержащими обе зеркальные плоскости T d и T h. Эта группа изоморфна S 4.C2и является полной группой симметрии куба и октаэдра. Это группа гипероктаэдра для n = 3. См. Также изометрии куба.
 Соединение куба и октаэдра
Соединение куба и октаэдра 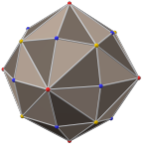 Каждая грань додекаэдра Дисдиакиса является фундаментальная область.
Каждая грань додекаэдра Дисдиакиса является фундаментальная область. 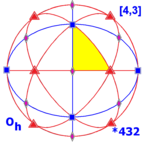 Группа октаэдра O h с фундаментальной областью
Группа октаэдра O h с фундаментальной областью С осями 4-го порядка в качестве координатных осей фундаментальная область Ohзадается как 0 ≤ x ≤ y ≤ z. Объект с этой симметрией характеризуется частью объекта в фундаментальной области, например, куб задается z = 1, а октаэдр - x + y + z = 1 (или соответствующие неравенства, чтобы вместо поверхности получить твердое тело). ax + by + cz = 1 дает многогранник с 48 гранями, например додекаэдр дисдякиса.
Грани 8 на 8 объединены в большие грани для a = b = 0 (куб) и 6 на 6 для a = b = c (октаэдр).
9 зеркальных линий полной октаэдрической симметрии можно разделить на две подгруппы 3 и 6 (нарисованные фиолетовым и красным цветом), представляющие две ортогональные подсимметрии: D2h и Td. Симметрия D 2h может быть увеличена вдвое до D 4h путем восстановления двух зеркал из одной из трех ориентаций.
| Октаэдрическая симметрия и отражающие подгруппы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Возьмите набор всех матриц перестановок 3x3 и назначьте знак + или знак - каждой из трех единиц. Всего имеется 6 матриц x 8 перестановок знаков = 48 матриц, дающих полную группу октаэдра. Существует ровно 24 матрицы с детерминантом = +1, и это матрицы вращения киральной октаэдрической группы. Остальные 24 матрицы соответствуют отражению или инверсии.
Для октаэдрической симметрии необходимы три матрицы отражательных генераторов, которые представляют три зеркала диаграммы Кокстера-Дынкина. Продукт отражений производят 3 вращающихся генератора.
| Отражения | Вращения | |||||
|---|---|---|---|---|---|---|
| Имя | R0 | R1 | R2 | R0R1 | R1R2 | R0R2 |
| Группа | ||||||
| Порядок | 2 | 2 | 2 | 4 | 3 | 2 |
| Матрица | ||||||
 O O Td Td ThЦиклические графы подгрупп порядка 24 ThЦиклические графы подгрупп порядка 24 |
 Подгруппы, упорядоченные в диаграмме Хассе Подгруппы, упорядоченные в диаграмме Хассе |
 Вращательные подгруппы Вращательные подгруппы 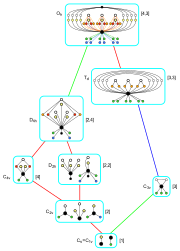 Отражающие подгруппы Отражающие подгруппы  Подгруппы, содержащие инверсия Подгруппы, содержащие инверсия |
| Schoe. | Coxeter | Orb. | HM | Structure | Cyc. | Order | Index | |
|---|---|---|---|---|---|---|---|---|
| Oh | [4,3] | * 432 | м3 м | S4 ×S2 | 48 | 1 | ||
| Td | [3,3] | * 332 | 43 м | S4 | 24 | 2 | ||
| D4h | [2,4] | * 224 | 4 / ммм | Dih 1 × Dih 4 | 16 | 3 | ||
| D2h | [2,2] | * 222 | ммм | Dih 1 = Dih 1×Didiv class="ht" | 8 | 6 | ||
| C4v | [4pting | *44 | 4mm | Dih 4 | 8 | 6 | ||
| C3v | [3] | * 33 | 3m | Dih 3=S3 | 6 | 8 | ||
| C2v | [ 2] | * 22 | мм2 | Dih 2 | 4 | 12 | ||
| Cs=C1v | [] | * | 2 или m | Dih 1 | 2 | 24 | ||
| Th | [3,4] | 3 * 2 | m3 | A4 ×S2 | 24 | 2 | ||
| C4h | [4,2] | 4* | 4 / м | Z4 × Dih 1 | 8 | 6 | ||
| D3d | [2,6] | 2 * 3 | 3m | Dih 6=Z2× Dih 3 | 12 | 4 | ||
| D2d | [2,4] | 2 * 2 | 42m | Dih 4 | 8 | 6 | ||
| C2h= D 1d | [2,2] | 2* | 2 / м | Z2× Dih 1 | 4 | 12 | ||
| S6 | [2,6] | 3× | 3 | Z6=Z2×Z3 | 6 | 8 | ||
| S4 | [2,4] | 2× | 4 | Z4 | 4 | 12 | ||
| S2 | [2,2] | × | 1 | S2 | 2 | 24 | ||
| O | [4,3] | 432 | 432 | S4 | 24 | 2 | ||
| T | [3,3] | 332 | 23 | A4 | 12 | 4 | ||
| D4 | [2,4] | 224 | 422 | Dih 4 | 8 | 6 | ||
| D3 | [2,3] | 223 | 322 | Дих 3=S3 | 6 | 8 | ||
| D2 | [2,2] | 222 | 222 | Дих 2=Z2 | 4 | 12 | ||
| C4 | [4] | 44 | 4 | Z4 | 4 | 12 | ||
| C3 | [3] | 33 | 3 | Z3=A3 | 3 | 16 | ||
| C2 | [2] | 22 | 2 | Z2 | 2 | 24 | ||
| C1 | [] | 11 | 1 | Z1 | 1 | 48 | ||
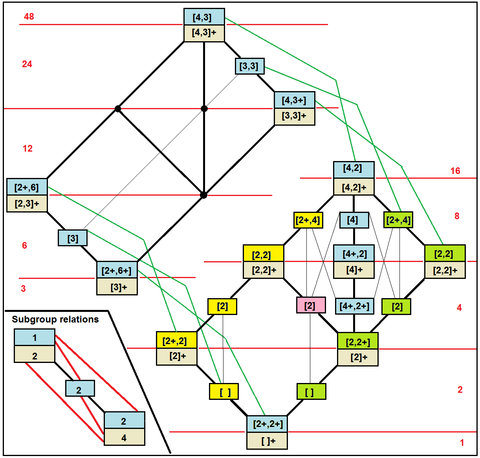 |
| Октаэдрические подгруппы в Обозначение Кокстера |
 48 элементы симметрии куба
48 элементы симметрии куба Куб имеет 48 изометрий (элементов симметрии), образующих группу симметрии Oh, изоморфную S4 × C 2. Их можно разделить на следующие категории:
Изометрию куба можно определить различными способами:
Для кубиков с цветами или маркировкой (например, кубики имеют), группа симметрии является подгруппой O h.
Примеры:
Для некоторых больших подгрупп куб с этой группой в качестве группы симметрии невозможно, просто раскрасьте целые грани. На лицах нужно нарисовать какой-то узор.
Примеры:
Полная симметрия куба, O h, [4,3], ( * 432), сохраняется тогда и только тогда, когда все грани имеют одинаковый узор, так что сохраняется полная симметрия квадрата, а для квадрата - группа симметрии, Dih 4, [4], порядка 8.
Полная симметрия куба относительно собственных вращений, O, [4,3], (432), сохраняется тогда и только тогда, когда все грани имеют тот же образец с 4-кратной вращательной симметрией , C 4, [4].
В теории римановых поверхностей поверхность Больца, иногда называемая кривой Больца, получается как разветвленная двойное покрытие сферы Римана с местом ветвления на множестве вершин правильного вписанного октаэдра. Его группа автоморфизмов включает гиперэллиптическую инволюцию, переворачивающую два листа покрытия. Фактор по подгруппе порядка 2, порожденной гиперэллиптической инволюцией, дает в точности группу симметрий октаэдра. Среди многих замечательных свойств поверхности Больца - тот факт, что она максимизирует систолу среди всех гиперболических поверхностей рода 2.
| Класс | Название | Изображение | Грани | Ребра | Вершины | Двойное имя | Изображение |
|---|---|---|---|---|---|---|---|
| Архимедово твердое тело. (Каталонское твердое тело ) | курносый куб |  | 38 | 60 | 24 | пятиугольный икоситетраэдр |  |
| Класс | Имя | Изображение | Грани | Ребра | Вершины | Двойное имя | Изображение |
|---|---|---|---|---|---|---|---|
| Платоново твердое тело | Куб |  | 6 | 12 | 8 | Октаэдр |  |
| Архимедово твердое тело. (двойное Каталонское твердое тело ) | Кубооктаэдр |  | 14 | 24 | 12 | Ромбический додекаэдр |  |
| Усеченный куб |  | 14 | 36 | 24 | Октаэдр триакиса |  | |
| Усеченный октаэдр |  | 14 | 36 | 24 | Гексаэдр Тетракиса |  | |
| Ромбокубооктаэдр |  | 26 | 48 | 24 | Дельтоидальный икоситетраэдр |  | |
| Усеченный кубооктаэдр | |||||||
 Дисциплина 48 Дисциплина 48 |  | ||||||
| Правильный. составной. многогранник | Стелла octangula |  | 8 | 12 | 8 | Самодвойственный | |
| Куб и октаэдр |  | 14 | 24 | 14 | Самодвойственный |