В математике и особенно в дифференциальной геометрии и манометре теория, соединение на пучке волокон - это устройство, которое определяет понятие параллельного транспорта на пучке; то есть способ «соединить» или идентифицировать волокна в близлежащих точках. Наиболее распространенный случай - это линейное соединение на векторном пакете , для которого понятие параллельного транспорта должно быть линейным. Линейная связь эквивалентно определяется ковариантной производной , оператором, который дифференцирует секции пучка вдоль касательных направлений в базовом многообразии таким образом, что параллельные участки имеют нулевую производную. Линейные связности обобщают на произвольные векторные расслоения связь Леви-Чивиты на касательном расслоении к риманову многообразию, которое дает стандартный способ дифференцировать векторные поля. Нелинейные связи обобщают это понятие на расслоения, слои которых не обязательно линейны.
Линейные связи также называются связями Кошуля в честь Жана-Луи Кошуля, который дал алгебраическую основу для их описания (Koszul 1950).
В этой статье связь в векторном пучке определяется с использованием общепринятой математической нотации, которая не выделяет координаты. Однако также регулярно используются другие обозначения: в общей теории относительности вычисления векторных расслоений обычно записываются с использованием индексированных тензоров; в калибровочной теории подчеркиваются эндоморфизмы слоев векторного пространства. Различные обозначения эквивалентны, как обсуждалось в статье о метрических связях (сделанные там комментарии относятся ко всем векторным связкам).
Содержание
- 1 Мотивация
- 2 Формальное определение
- 3 Индуцированные связи
- 4 Внешние ковариантные производные и векторные формы
- 5 Аффинные свойства набора связей
- 6 Отношение к главная и связь Эресмана
- 7 Локальное выражение
- 8 Параллельный перенос и голономия
- 9 Кривизна
- 9.1 Локальная форма и уравнение структуры Картана
- 9.2 Тождество Бианки
- 10 Калибровочные преобразования
- 11 Примеры
- 12 См. Также
- 13 Ссылки
Мотивация
Часть векторного расслоения обобщает понятие функции на многообразии в том смысле, что стандартная вектор-функция  можно рассматривать как часть тривиального векторного расслоения
можно рассматривать как часть тривиального векторного расслоения  . Поэтому естественно спросить, можно ли дифференцировать сечение по аналогии с тем, как дифференцировать векторное поле. Когда векторное расслоение является касательным расслоением к римановому многообразию, на этот вопрос естественным образом отвечает связность Леви-Чивита, которая является единственной связностью без кручения. совместим с римановой метрикой на касательном расслоении. Вообще такого естественного выбора способа разграничения разделов нет.
. Поэтому естественно спросить, можно ли дифференцировать сечение по аналогии с тем, как дифференцировать векторное поле. Когда векторное расслоение является касательным расслоением к римановому многообразию, на этот вопрос естественным образом отвечает связность Леви-Чивита, которая является единственной связностью без кручения. совместим с римановой метрикой на касательном расслоении. Вообще такого естественного выбора способа разграничения разделов нет.
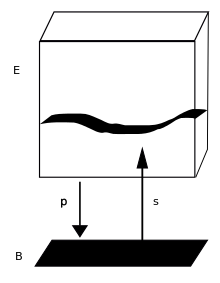
Сечение расслоения можно рассматривать как обобщенную функцию от основания к слоям векторного расслоения. Это можно визуализировать с помощью графика разреза, как на рисунке выше.
Пример модели - дифференцировать  -компонентное векторное поле
-компонентное векторное поле  в евклидовом пространстве
в евклидовом пространстве  . В этой настройке производная
. В этой настройке производная  в точке
в точке  в направлении
в направлении  может быть просто определено как
может быть просто определено как

Обратите внимание, что для каждого  , мы определили новый вектор
, мы определили новый вектор  , поэтому производная от
, поэтому производная от  в направлении
в направлении  дало новое
дало новое  -компонентное векторное поле на
-компонентное векторное поле на  .
.
При переходе к разделу  векторного расслоения
векторного расслоения  на коллекторе
на коллекторе  , с этим определением возникают две ключевые проблемы. Во-первых, поскольку многообразие не имеет линейной структуры, термин
, с этим определением возникают две ключевые проблемы. Во-первых, поскольку многообразие не имеет линейной структуры, термин  не имеет смысла на
не имеет смысла на  . Вместо этого выбирается путь
. Вместо этого выбирается путь  такой, что
такой, что  и вычисляет
и вычисляет

Однако это все еще не имеет смысла, потому что  - вектор в волокне над
- вектор в волокне над  , а
, а  , волокно над
, волокно над  , которое представляет собой другое векторное пространство. Это означает, что нет никакого смысла в вычитании этих двух членов, лежащих в разных векторных пространствах.
, которое представляет собой другое векторное пространство. Это означает, что нет никакого смысла в вычитании этих двух членов, лежащих в разных векторных пространствах.
Цель состоит в том, чтобы решить вышеупомянутую загадку, придумав способ дифференцировать секции векторного расслоения в направлении векторных полей и получить обратно другой участок векторного расслоения. Есть три возможных решения этой проблемы. Все три требуют выбора того, как различать сечения, и только в особых условиях, таких как касательное расслоение на римановом многообразии, есть естественный такой выбор.
- (Параллельный перенос ) Поскольку проблема в том, что векторы
 и
и  лежат в разных волокнах
лежат в разных волокнах  , одно решение - определить изоморфизм
, одно решение - определить изоморфизм  для всех
для всех  близко к нулю. Используя этот изоморфизм, можно переместить
близко к нулю. Используя этот изоморфизм, можно переместить  в волокно
в волокно  а потом учтите разницу. Явно
а потом учтите разницу. Явно

- Это параллельный транспорт и выбор изоморфизмов
 для всех кривых
для всех кривых  в
в  можно рассматривать как определение того, как различать сечение.
можно рассматривать как определение того, как различать сечение.
- (Связь Эресмана ) Используйте понятие дифференциала отображения гладких многообразий. Раздел
 по определению является гладкой картой
по определению является гладкой картой  , так что
, так что  . Это имеет дифференциал
. Это имеет дифференциал  со свойством, что
со свойством, что  для векторного поля
для векторного поля  . Однако вместо этого хотелось бы, чтобы
. Однако вместо этого хотелось бы, чтобы  был частью самого
был частью самого  . Фактически, вертикальный пучок
. Фактически, вертикальный пучок  является откатом от
является откатом от  вдоль
вдоль  с тем же волокном, что и
с тем же волокном, что и  . Если выбрать проекцию векторных пучков
. Если выбрать проекцию векторных пучков  , композиция с этой проекцией приведет к
, композиция с этой проекцией приведет к  обратно в
обратно в  . Это называется линейной связностью Эресмана на векторном расслоении
. Это называется линейной связностью Эресмана на векторном расслоении  . Существует множество вариантов операторов проекции
. Существует множество вариантов операторов проекции  , поэтому в целом существует много разных способов дифференцирования векторного поля.
, поэтому в целом существует много разных способов дифференцирования векторного поля.
- (Ковариантный производная ) Третье решение состоит в том, чтобы абстрагироваться от свойств, которыми должна обладать производная от части векторного расслоения, и принимать это как аксиоматическое определение. Это понятие связи или ковариантной производной, описанное в этой статье. Два других вышеуказанных подхода могут быть эквивалентны этому аксиоматическому определению дифференцирования.
Формальное определение
Пусть E → M будет гладким векторным расслоением над дифференцируемое многообразие М. Обозначим пространство гладких сечений множества E через Γ (E). A соединение на E является ℝ- линейным отображением

такая, что правило Лейбница

выполняется для всех гладких функций f на M и всех гладких сечений σ множества E.
Если X - касательная векторное поле на M (т.е. часть касательного пучка TM) можно определить ковариантную производную по X

путем сжатия X с полученным ковариантным индексом в соединении: ∇ X σ = (∇σ) (X). Ковариантная производная удовлетворяет следующим условиям:

И наоборот, любой оператор, удовлетворяющий указанным выше свойствам, определяет соединение на E, и соединение в этом смысле также известно как ковариантная производная на E.
Индуцированные соединения
Учитывая векторный набор  , существует множество связанных пакетов с
, существует множество связанных пакетов с  , которые могут быть построены, например двойное векторное расслоение
, которые могут быть построены, например двойное векторное расслоение  , тензорные степени
, тензорные степени  , симметричные и антисимметричные тензорные степени
, симметричные и антисимметричные тензорные степени  и директ t суммы
и директ t суммы  . Соединение на
. Соединение на  индуцирует соединение на любом из этих связанных пакетов. Простота перехода между связями на ассоциированных связках более элегантно описывается теорией основных связок пучков, но здесь мы представляем некоторые из основных индуцированных связей.
индуцирует соединение на любом из этих связанных пакетов. Простота перехода между связями на ассоциированных связках более элегантно описывается теорией основных связок пучков, но здесь мы представляем некоторые из основных индуцированных связей.
Учитывая  соединение на
соединение на  , индуцированное двойное соединение
, индуцированное двойное соединение  на
на  определяется
определяется

Здесь  - гладкое векторное поле,
- гладкое векторное поле,  - это часть
- это часть  и
и  раздел двойного пакета и
раздел двойного пакета и  естественное соединение между векторным пространством и двойственным ему (происходит на каждом волокне между
естественное соединение между векторным пространством и двойственным ему (происходит на каждом волокне между  и
и  ). Обратите внимание, что это определение, по сути, предписывает, чтобы
). Обратите внимание, что это определение, по сути, предписывает, чтобы  было соединением на
было соединением на  так, чтобы естественное правило произведения удовлетворялось для пары
так, чтобы естественное правило произведения удовлетворялось для пары  .
.
Учитывая  соединения на двух векторных пучках
соединения на двух векторных пучках  , определите связь тензорного произведения по формуле
, определите связь тензорного произведения по формуле

Здесь  . Обратите внимание, что это естественный способ объединения
. Обратите внимание, что это естественный способ объединения  , чтобы обеспечить соблюдение правила произведения для связи тензорного произведения. Аналогичным образом определите связь с прямой суммой как
, чтобы обеспечить соблюдение правила произведения для связи тензорного произведения. Аналогичным образом определите связь с прямой суммой как

где  .
.
Поскольку внешняя мощность и симметричная мощность вектора пучок можно рассматривать как подпространства тензорной степени,  , определение связи тензорного произведения прямо применяется к этой настройке. А именно, если
, определение связи тензорного произведения прямо применяется к этой настройке. А именно, если  является соединением на
является соединением на  , у него соединение с тензорным питанием Путем повторного применения вышеупомянутого соединения тензорного произведения. У нас также есть симметричная связь продукта, определяемая как
, у него соединение с тензорным питанием Путем повторного применения вышеупомянутого соединения тензорного произведения. У нас также есть симметричная связь продукта, определяемая как

и внешнее соединение продукта, определенное

для всех  . Повторное применение этих продуктов дает наведенное симметричное питание и внешние силовые соединения на
. Повторное применение этих продуктов дает наведенное симметричное питание и внешние силовые соединения на  и
и  соответственно.
соответственно.
Наконец, получается индуцированная связь  на векторном расслоении
на векторном расслоении  , связь эндоморфизма . Это просто тензорное произведение двойного соединения
, связь эндоморфизма . Это просто тензорное произведение двойного соединения  на
на  и
и  на
на  . Если
. Если  и
и  , так что композиция
, так что композиция  , то выполняется следующее правило произведения:
, то выполняется следующее правило произведения:

Внешняя ковариантная производная и векторнозначные формы
Пусть E → M - векторное расслоение. E-значная дифференциальная форма степени r является частью пучка тензорного произведения :

Пространство таких форм обозначается

E-значная 0-форма - это просто сечение расслоения E. То есть

В этих обозначениях связь на E → M является линейным отображением

Тогда соединение можно рассматривать как обобщение внешней производной к векторным расслоенным значным формам. Фактически, для связности ∇ на E существует единственный способ продолжить ∇ до внешней ковариантной производной

В отличие от обычной внешней производной, обычно (d) ≠ 0. Фактически, (d) напрямую связано с кривизной соединения ∇ (см. ниже).
Аффинные свойства множества связностей
Каждое векторное расслоение над многообразием допускает связь, что может быть доказано с помощью разбиений единицы. Однако связи не уникальны. Если ∇ 1 и ∇ 2 - две связи на E → M, то их различие представляет собой C -линейный оператор. То есть

для всех гладких функций f на M и всех гладких сечений σ множества E. Отсюда следует, что разность ∇ 1 - ∇ 2 индуцируется одной формой на M со значениями в расслоении эндоморфизмов End (E) = E⊗E *:

И наоборот, если ∇ - соединение на E и A - одноформа на M со значениями в End (E), тогда ∇ + A - связность на E.
Другими словами, пространство связностей на E - это аффинное пространство для Ω (конец E). Это аффинное пространство обычно обозначается  .
.
Отношение к основным связям и связям Эресмана
Пусть E → M - векторное расслоение ранга k и пусть F (E) быть основным пакетом кадров E. Затем (главное) соединение на F (E) индуцирует соединение на E. Сначала обратите внимание, что разделы E находятся во взаимно однозначном соответствии с правоэквивариантными отображениями F (E) → R . (Это можно увидеть, рассматривая откат E над F (E) → M, который изоморфен тривиальному пучку F (E) × R .) Для сечения σ множества E пусть соответствующее эквивариантное отображение есть ψ (σ). Ковариантная производная на E тогда определяется выражением

где X - горизонтальный подъем X от M до F (E). (Напомним, что горизонтальный подъем определяется связностью на F (E).)
И наоборот, связность на E определяет связность на F (E), и эти две конструкции взаимно обратны.
Соединение на E также определяется эквивалентным образом с помощью линейного соединения Эресмана на E. Это обеспечивает один метод для построения ассоциированного главного соединения.
Локальное выражение
Пусть E → M - векторное расслоение ранга k, и пусть U - открытое подмножество M, над которым E тривиально. Для локальной гладкой шкалы (e1,..., e k) E над U, любое сечение σ матрицы E можно записать как  (предполагается нотация Эйнштейна ). Связь на E, ограниченная U, тогда принимает вид
(предполагается нотация Эйнштейна ). Связь на E, ограниченная U, тогда принимает вид

что означает, учитывая каждый компонент:

где

Здесь  определяет матрицу 1-форм размера k × k на U. Фактически, для любой такой матрицы приведенное выше выражение определяет связь на E, ограниченную U. Это потому что
определяет матрицу 1-форм размера k × k на U. Фактически, для любой такой матрицы приведенное выше выражение определяет связь на E, ограниченную U. Это потому что  определяет одноформу ω со значениями в End (E), и это выражение определяет ∇ быть связностью d + ω, где d - тривиальная связность на E над U, определяемая дифференцированием компонентов секции с помощью локальной шкалы. В этом контексте ω иногда называют формой соединения по отношению к локальному кадру.
определяет одноформу ω со значениями в End (E), и это выражение определяет ∇ быть связностью d + ω, где d - тривиальная связность на E над U, определяемая дифференцированием компонентов секции с помощью локальной шкалы. В этом контексте ω иногда называют формой соединения по отношению к локальному кадру.
Если U - координатная окрестность с координатами (x), то мы можем записать

Обратите внимание на сочетание координатных индексов (i) и волокон (α, β) в этом выражении.
Коэффициентные функции  тензорны в индекс i (они определяют одну форму), но не в индексах α и β. Закон преобразования для показателей волокна более сложный. Пусть (f 1,..., f k) будет другим гладким локальным кадром над U, и пустьизменение координатной матрицы будет обозначено t, то есть:
тензорны в индекс i (они определяют одну форму), но не в индексах α и β. Закон преобразования для показателей волокна более сложный. Пусть (f 1,..., f k) будет другим гладким локальным кадром над U, и пустьизменение координатной матрицы будет обозначено t, то есть:

Матрица связи по отношению к кадру (f α) тогда задается матричным выражением

Здесь dt - матрица единичных форм, полученная взятием внешней производной компонентов t.
Ковариантная производная в локальных координатах и по полю локализации системы отсчета (e α) задается выражением

Например, если мы насыщаем нижний индекс аргумента ∇ базисным касательным вектором  и установить
и установить  , мы имеем:
, мы имеем:

Параллельный перенос и голономия
Связность ∇ на векторном расслоении E → M сущность параллельного на E вдоль кривой кривой в M. Пусть γ: [0, 1] → M - гладкий путь в M. Сечение σ точки E вдоль γ называется параллельным, если

для всех t ∈ [0, 1 ]. Эквивалентно, можно рассматривать обратное расслоение γ * E для E через γ. Это векторное расслоение над [0, 1] со слоем E γ (t) над t ∈ [0, 1]. Связь ∇ на E переходит в связь на γ * E. Участок σ отрезка γ * E параллелен тогда и только тогда, когда γ * ∇ (σ) = 0.
Предположим, что γ - это путь от x к y в M. Приведенное выше уравнение, определяющее параллельные участки, является первым - Порядок обыкновенное уравнение (см. локальное выражение выше) и поэтому имеет уникальное решение для каждого возможного начального условия. То есть для каждого изображения v в E x существует уникальный параллельный участок σ из γ * E с σ (0) = v. Определите параллельную транспортную карту

на τ γ (v) = σ (1). Можно показать, что τ γ - это линейный изоморфизм.
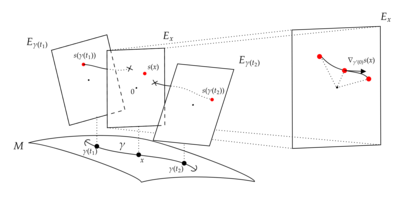
Как восстановить ковариантную производную соединения из его параллельного переноса. Значения

секции

переносятся параллельно по пути

обратно к

, а берется ковариантная производная в фиксированном векторном пространстве, слой

над

.
Параллельный перенос может группы отопления для установки соединения ∇ на основе точки x в M. Это подгруппа GL (E x), состоящий из всех параллельных транспортных карт, поступающих из петель на основе x:

Группа голономии связного с кривизной соединения (AmbroseSinger 1953).
Соединение может быть восстановлено от его параллельных транспортных операторов следующим образом. Если  - новое поле и
- новое поле и  сечение в точке
сечение в точке  выберите интегральную кривую
выберите интегральную кривую  для
для  при
при  . Для каждого
. Для каждого  мы будем писать
мы будем писать  для параллельной транспортной карты, путешествующей по
для параллельной транспортной карты, путешествующей по  от
от  до
до  . В частности, для каждого
. В частности, для каждого  мы имеем
мы имеем  . Тогда
. Тогда  определить кривую в векторном пространстве
определить кривую в векторном пространстве  , которые можно различать. Ковариантная производная восстанавливается как
, которые можно различать. Ковариантная производная восстанавливается как

Это демонстрирует, что эквивалентное определение соединения путем указания всех параллельных транспортных изоморфизмов  между волокнами
между волокнами  и взяв указанное выше выражение как определение
и взяв указанное выше выражение как определение  .
.
Curvature
curvature связности ∇ на E → M представляет собой 2-форму F на M со значениями в расслоении эндоморфизмов End (E) = E⊗E *. То есть

Он определяется выражением
![F ^ {\ nabla} (X, Y) ( s) = \ nabla _ {X} \ nabla _ {Y} s- \ nabla _ {Y} \ nabla _ {X} s- \ nabla _ {{[X, Y]}} s](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c313567e9cee5ede2aed07f2309d61705b22856)
где X и Y - касательные поля на M, а s - часть E. Необходимо проверить, что F C -линеен как по X, так и по Y, и что оно действительно определить эндоморфизм расслоения E.
Как включается выше, ковариантная внешняя производная d не должна возводиться в ноль при действии на E-значные формы. Однако оператор (d) строго тензорный (то есть есть C-линейный). Это означает, что он индуцирован 2-со значениями в конце (E). Эта 2-форма в точности соответствует приведенной выше форме кривизны. Для E-значной формы σ имеем

A плоское соединение - это соединение, форма кривизны которого одинаково равна нулю.
Локальная форма и уравнение структуры Картана
Форма кривизны имеет локальное описание, называемое структурным уравнением Картана . Если  имеет локальную форму
имеет локальную форму  в некотором упрощающем открытом подмножестве
в некотором упрощающем открытом подмножестве  для
для  , затем
, затем

на  . Чтобы уточнить,
. Чтобы уточнить,  , где
, где  - однозначная эндоморфизмозначная форма. Для простоты предположим, что
- однозначная эндоморфизмозначная форма. Для простоты предположим, что  для единственной формы
для единственной формы  и эндоморфизм
и эндоморфизм  . Затем мы используем
. Затем мы используем

где  - еще одна форма эндоморфизма со значением одной формы. В общем случае
- еще одна форма эндоморфизма со значением одной формы. В общем случае  будет этой суммой простых тензоров формы, а операторы
будет этой суммой простых тензоров формы, а операторы  и
и  расширяются линейно.
расширяются линейно.
Можно проверить, что если мы определим ![{\ displayst yle [\ omega, \ omega]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49781158c85571db177c1be54ffd2419bbfc109e) как произведение клина форм, но коммутатор эндоморфизмов в противоположность композиции, то
как произведение клина форм, но коммутатор эндоморфизмов в противоположность композиции, то ![{\ displaystyle \ omega \ клин \ omega = {\ frac {1} {2}} [\ omega, \ omega]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff61d53b3050f819bee0b8347b02ce44066277b) , и с этим альтернативным обозначением структурное уравнение Картана принимает вид
, и с этим альтернативным обозначением структурное уравнение Картана принимает вид
![{\ displaystyle F ^ {\ nabla} = d \ omega + {\ frac {1} {2}} [\ omega, \ omega].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfff0c032e9b116f25a91ca11c6491eeb521555e)
Это альтернативное обозначение обычно используется в теории основных связок пучков, где форма связи  - это алгебра Ли -значная однозначная форма, для которой нет понятия композиции (в отличие от случая эндоморфизмов), но есть понятие скобки Ли.
- это алгебра Ли -значная однозначная форма, для которой нет понятия композиции (в отличие от случая эндоморфизмов), но есть понятие скобки Ли.
В некоторых ссылках структурное уравнение Картана может быть записано со знаком минус:

В этом другом соглашении используется порядок умножения матриц, отличный от стандартной нотации Эйнштейна в произведении клина матричнозначных одноформные.
Тождество Бьянки
Версия тождества Бьянки из римановой геометрии верна для связности на любом векторном расслоении. Напомним, что соединение  на векторном расслоении
на векторном расслоении  индуцирует соединение эндоморфизма на
индуцирует соединение эндоморфизма на  . Эта связь эндоморфизма имеет внешнюю ковариантную производную, которую мы неоднозначно называем
. Эта связь эндоморфизма имеет внешнюю ковариантную производную, которую мы неоднозначно называем  . Поскольку кривизна - это глобально определенная
. Поскольку кривизна - это глобально определенная  -значная двухформа, мы можем применить к ней внешнюю ковариантную производную. Тождество Бьянки гласит, что
-значная двухформа, мы можем применить к ней внешнюю ковариантную производную. Тождество Бьянки гласит, что
 .
.
Это лаконично отражает сложные тензорные формулы Тождество Бианки в случае римановых многообразий, и можно перевести это уравнение в стандартные тождества Бианки, расширив связность и кривизну в локальных координатах.
Преобразования датчика
Даны две связи  на векторный набор
на векторный набор  , естественно спросить, когда они могут считаться эквивалентными. Существует четко определенное понятие автоморфизма векторного расслоения
, естественно спросить, когда они могут считаться эквивалентными. Существует четко определенное понятие автоморфизма векторного расслоения  . Секция
. Секция  является автоморфизмом, если
является автоморфизмом, если  обратимо в каждой точке
обратимо в каждой точке  . Такой автоморфизм называется калибровочным преобразованием элемента
. Такой автоморфизм называется калибровочным преобразованием элемента  , а группа всех автоморфизмов называется калибровочной группой, часто обозначается
, а группа всех автоморфизмов называется калибровочной группой, часто обозначается  или
или  . Группу калибровочных преобразований можно аккуратно охарактеризовать как пространство сечений сопряженного пучка A
. Группу калибровочных преобразований можно аккуратно охарактеризовать как пространство сечений сопряженного пучка A  из пакета кадров векторного пакета
из пакета кадров векторного пакета  . Это не следует путать со строчными буквами a присоединенный набор
. Это не следует путать со строчными буквами a присоединенный набор  , который естественно отождествляется с самим
, который естественно отождествляется с самим  . Пакет
. Пакет  - это связанный пакет с основным фреймом связка представлением конъюгации
- это связанный пакет с основным фреймом связка представлением конъюгации  на себе,
на себе,  и имеет слой той же общей линейной группы
и имеет слой той же общей линейной группы  где
где  . Обратите внимание, что, несмотря на то, что у пакета фреймов
. Обратите внимание, что, несмотря на то, что у пакета фреймов  то же волокно и он связан с ним,
то же волокно и он связан с ним,  не совпадает ни с пакетом кадров, ни даже с самим основным пакетом. Калибровочную группу можно эквивалентно охарактеризовать как
не совпадает ни с пакетом кадров, ни даже с самим основным пакетом. Калибровочную группу можно эквивалентно охарактеризовать как 
Преобразование датчика  из
из  действует на разделы
действует на разделы  , поэтому действует на соединение путем сопряжения. Явно, если
, поэтому действует на соединение путем сопряжения. Явно, если  является соединением на
является соединением на  , то определяется
, то определяется  по
по

для  . Чтобы проверить, что
. Чтобы проверить, что  является соединением, проверяется правило произведения
является соединением, проверяется правило произведения

Можно проверить, что это определяет левое действие груп пы из  на тонкое пространство всех соединений
на тонкое пространство всех соединений  .
.
Время  моделируется аффинным пространством на
моделируется аффинным пространством на  должен существовать некоторый эндоморфизм - однозначная однозначная форма
должен существовать некоторый эндоморфизм - однозначная однозначная форма  такой, что
такой, что  . Используя определение связи эндоморфизма
. Используя определение связи эндоморфизма  , вызванной
, вызванной  , видно, что
, видно, что

то есть  .
.
Две связи называются калибровочными эквивалентами, если они отличаются калибровочной группы и факторпространством  - это пространство модулей всех соединений на
- это пространство модулей всех соединений на  . В общем, это топологическое пространство не является ни гладким многообразием, ни даже хаусдорфовым пространством, но содержит внутри пространство модулей связностей Янга - Миллса на
. В общем, это топологическое пространство не является ни гладким многообразием, ни даже хаусдорфовым пространством, но содержит внутри пространство модулей связностей Янга - Миллса на  , который представляет значительный интерес в калибровочной теории и физике.
, который представляет значительный интерес в калибровочной теории и физике.
Примеры
- Классическая ковариантная производная или аффинная связь создать соединение на касательном пучке M, или в более общем смысле, на любом тензорном пучке, образованном путем взятия тензорных произведений касательного пучка на себя и его двойное.
- Соединение на
 можно явно описать как оператор
можно явно описать как оператор

- где
 - внешняя производная, вычисляемая по векторному значению гладкие функции и
- внешняя производная, вычисляемая по векторному значению гладкие функции и  гладкие. Участок
гладкие. Участок  можно отождествить картой
можно отождествить картой 
- , а затем

- Если пакет снабжен метрикой пакет, внутреннимтом на его волоконнах пространства продуктивы, соединение метрики определяет как соединение, которое совместимо с метрикой пакет.
- A Связь Янга-Миллса - это специальная метрическая связь, которая удовлетворяет уравнениям Янга-Миллса движения.
- A Риманова связность - это метрическая связность на касательном расслоении риманова многообразия.
- A Связность Леви-Чивита является модельной римановой связностью: явое с метрикой соединение на касательном пучке, которое также не имеет кручения. Она уникальна в том смысле, что для любого римановой связности всегда можно найти одну и только одну эквивалентную связь, не имеющую кручения. «Эквивалентный» означает, что он соответствовал одной и той же метрикой, хотя тензоры кривизны могут быть разными; см. телепараллелизм. Леви-Чивиты задаются тензором .
- . Внешняя производная является плоской связью на
 (тривиальное линейное расслоение над M).
(тривиальное линейное расслоение над M). - В более общем плане существует плоская плоская связность на любом канале плоском векторном расслоении (т. Е. который вектор расслоение, все функции перехода которого постоянны), задается внешней производной в любой тривиализации.
См. Также
Ссылки
- Chern, Shiing-Shen (1951), Topics in Differential Geometry, Institute for Advanced Study, мимеографические записи лекций
- Darling, RWR (1994), Дифференциальные формы и связи, Кембридж, Великобритания: Cambridge University Press, ISBN 0-521-46800-0
- Кобаяси, Шошичи; Номидзу, Кацуми (1996) [1963], Основы дифференциальной геометрии, Vol. 1, Wiley Classics Library, Нью-Йорк: Wiley Interscience, ISBN 0-471-15733-3
- Кошул, JL (1950), "Homologie et cohomologie des algebres de Lie ", Bulletin de la Société Mathématique, 78 : 65–127
- Wells, RO (1973), Дифференциальный анализ комплексных многообразий, Springer-Verlag, ISBN 0-387-90419-0
- Амвросий, Вашингтон; Сингер, И.М. (1953), «Теорема о голономии», Труды Американского математического общества, 75 : 428–443, doi : 10.2307 / 1990721


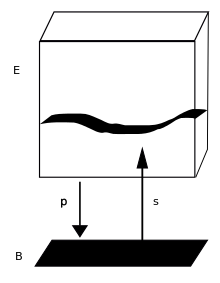 Сечение расслоения можно рассматривать как обобщенную функцию от основания к слоям векторного расслоения. Это можно визуализировать с помощью графика разреза, как на рисунке выше.
Сечение расслоения можно рассматривать как обобщенную функцию от основания к слоям векторного расслоения. Это можно визуализировать с помощью графика разреза, как на рисунке выше. 
























 и
и  лежат в разных волокнах
лежат в разных волокнах  , одно решение - определить изоморфизм
, одно решение - определить изоморфизм  для всех
для всех  близко к нулю. Используя этот изоморфизм, можно переместить
близко к нулю. Используя этот изоморфизм, можно переместить  в волокно
в волокно  а потом учтите разницу. Явно
а потом учтите разницу. Явно
 для всех кривых
для всех кривых  в
в  можно рассматривать как определение того, как различать сечение.
можно рассматривать как определение того, как различать сечение. по определению является гладкой картой
по определению является гладкой картой  , так что
, так что  . Это имеет дифференциал
. Это имеет дифференциал  со свойством, что
со свойством, что  для векторного поля
для векторного поля  . Однако вместо этого хотелось бы, чтобы
. Однако вместо этого хотелось бы, чтобы  был частью самого
был частью самого  . Фактически, вертикальный пучок
. Фактически, вертикальный пучок  является откатом от
является откатом от  вдоль
вдоль  с тем же волокном, что и
с тем же волокном, что и  . Если выбрать проекцию векторных пучков
. Если выбрать проекцию векторных пучков  , композиция с этой проекцией приведет к
, композиция с этой проекцией приведет к  обратно в
обратно в  . Это называется линейной связностью Эресмана на векторном расслоении
. Это называется линейной связностью Эресмана на векторном расслоении  . Существует множество вариантов операторов проекции
. Существует множество вариантов операторов проекции  , поэтому в целом существует много разных способов дифференцирования векторного поля.
, поэтому в целом существует много разных способов дифференцирования векторного поля.











































































 Как восстановить ковариантную производную соединения из его параллельного переноса. Значения
Как восстановить ковариантную производную соединения из его параллельного переноса. Значения  секции
секции  переносятся параллельно по пути
переносятся параллельно по пути  обратно к
обратно к  , а берется ковариантная производная в фиксированном векторном пространстве, слой
, а берется ковариантная производная в фиксированном векторном пространстве, слой  над
над  .
.




















![F ^ {\ nabla} (X, Y) ( s) = \ nabla _ {X} \ nabla _ {Y} s- \ nabla _ {Y} \ nabla _ {X} s- \ nabla _ {{[X, Y]}} s](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c313567e9cee5ede2aed07f2309d61705b22856)

















![{\ displayst yle [\ omega, \ omega]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49781158c85571db177c1be54ffd2419bbfc109e)
![{\ displaystyle \ omega \ клин \ omega = {\ frac {1} {2}} [\ omega, \ omega]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ff61d53b3050f819bee0b8347b02ce44066277b)
![{\ displaystyle F ^ {\ nabla} = d \ omega + {\ frac {1} {2}} [\ omega, \ omega].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfff0c032e9b116f25a91ca11c6491eeb521555e)







 .
.










































 можно явно описать как оператор
можно явно описать как оператор
 - внешняя производная, вычисляемая по векторному значению гладкие функции и
- внешняя производная, вычисляемая по векторному значению гладкие функции и  гладкие. Участок
гладкие. Участок  можно отождествить картой
можно отождествить картой 

 (тривиальное линейное расслоение над M).
(тривиальное линейное расслоение над M).