Примеры векторных пространств

На этой странице перечислены некоторые примеры векторных пространств . См. векторное пространство для определения терминов, используемых на этой странице. См. Также: размер, базис.

Обозначения. Пусть F обозначает произвольное поле , такое как вещественные числа Rили комплексные числа C.

• 1 Простое или нулевое векторное пространство
• 2 Поле
• 3 Координатное пространство
• 4 Бесконечное координатное пространство
• 5 Произведение векторных пространств
• 6 Матрицы
• 7 Полиномиальные векторные пространства
  • 7.1 Одна переменная
  • 7.2 Несколько переменных
• 8 Функциональные пространства
  • 8.1 Обобщенное координатное пространство
  • 8.2 Линейные карты
  • 8.3 Непрерывные функции
  • 8.4 Дифференциальные уравнения
• 9 Расширения полей
• 10 Конечные векторные пространства
• 11 Примечания
• 12 Ссылки

Простейшим примером векторного пространства является тривиальный: {0}, который содержит только нулевой вектор (см. Третью аксиому в статье Векторное пространство ). Как сложение векторов, так и скалярное умножение тривиальны. базисом для этого векторного пространства является пустой набор, так что {0} является 0- -мерным векторным пространством над F. Каждое векторное пространство над F содержит подпространство , изоморфное этому.

Нулевое векторное пространство отличается от нулевого пространства линейного оператора L, который является ядром L.

Следующий простейший пример - это само поле F. Сложение векторов - это просто сложение полей, а скалярное умножение - это просто умножение полей. Это свойство можно использовать, чтобы доказать, что поле является векторным пространством. Любой ненулевой элемент F служит базисом, поэтому F является 1-мерным векторным пространством над собой.

Поле представляет собой довольно специфическое векторное пространство; на самом деле это простейший пример коммутативной алгебры над F. Кроме того, F имеет только два подпространства : {0} и сам F.

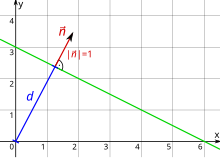Планарная аналитическая геометрия использует координатное пространство R . Изображено: описание строки как набора решений в $x\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{x\}\}\}$векторного уравнения $x\; \to \; \cdot \; n\; \to \; =\; d\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{x\}\}\; \backslash \; cdot\; \{\backslash \; vec\; \{n\}\}\; =\; d\}$.

Исходный пример векторного пространства следующий. Для любого положительного целого n, набор всех n-кортежей элементов F образует n-мерное векторное пространство над F, иногда называемое координатой пробел и обозначается F. Элемент F записывается

$x\; =\; (x\; 1,\; x\; 2,\dots ,\; xn)\; \{\backslash \; displaystyle\; x\; =\; (x\_\; \{1\},\; x\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\})\}$

, где каждый x i является элементом F. Операции с F определяются как

$x\; +\; y\; =\; (x\; 1\; +\; y\; 1,\; x\; 2\; +\; y\; 2,\dots ,\; Xn\; +\; yn)\; \{\backslash \; displaystyle\; x\; +\; y\; =\; (x\_\; \{1\}\; +\; y\_\; \{1\},\; x\_\; \{2\}\; +\; y\_\; \{2\},\; \backslash \; ldots,\; x\_\; \{n\}\; +\; y\_\; \{n\})\}$

$\alpha \; Икс\; знак\; равно\; (\alpha \; Икс\; 1,\; \alpha \; Икс\; 2,\dots ,\; \alpha \; Xn)\; \{\backslash \; Displaystyle\; \backslash \; альфа\; х\; =\; (\backslash \; альфа\; х\_\; \{1\},\; \backslash \; альфа\; х\_\; \{2\},\; \backslash \; ldots,\; \backslash \; альфа\; х\_\; \{п\})\}$

$0\; =\; (0,\; 0,\dots ,\; 0)\; \{\backslash \; displaystyle\; 0\; =\; (0,0,\; \backslash \; ldots,\; 0)\}$

$-\; x\; =\; (-\; x\; 1,\; -\; x\; 2,\dots ,\; -\; xn)\; \{\backslash \; displaystyle\; -x\; =\; (-\; x\_\; \{1\},\; -\; x\_\; \{2\},\; \backslash \; ldots,\; -x\_\; \{n\})\}$

Обычно F - это поле вещественных чисел, в этом случае мы получаем реальное координатное пространство R. Поле комплексных чисел дает комплексное координатное пространство C. Форма a + bi комплексного числа показывает, что C само по себе является двумерным вещественным векторным пространством с координатами (a, b). Аналогично, кватернионы и октонионы являются соответственно четырех- и восьмимерными действительными векторными пространствами, а C - это 2n-мерное реальное векторное пространство.

Векторное пространство F имеет стандартную основу :

$e\; 1\; =\; (1,\; 0,\dots ,\; 0)\; \{\backslash \; displaystyle\; e\_\; \{1\}\; =\; (1,0,\; \backslash \; ldots,\; 0)\; \}$

$е\; 2\; =\; (0,\; 1,\dots ,\; 0)\; \{\backslash \; displaystyle\; e\_\; \{2\}\; =\; (0,1,\; \backslash \; ldots,\; 0)\}$

$⋮\; \{\backslash \; displaystyle\; \backslash \; vdots\}$

$ru\; =\; (0,\; 0,\dots ,\; 1)\; \{\backslash \; displaystyle\; e\_\; \{n\}\; =\; (0,0,\; \backslash \; ldots,\; 1)\}$

где 1 обозначает мультипликативное тождество в F.

Пусть F обозначает пространство бесконечных последовательностей элементов из F таких, что только конечное число элементов ненулевое. То есть, если мы запишем элемент F как

$x\; =\; (x\; 1,\; x\; 2,\; x\; 3,\dots )\; \{\backslash \; displaystyle\; x\; =\; (x\_\; \{1\},\; x\_\; \{2\},\; x\_\; \{3\},\; \backslash \; ldots)\}$

, то только конечное число x i отличны от нуля (т. е. все координаты становятся нулевыми после определенной точки). Сложение и скалярное умножение задаются как в конечном координатном пространстве. Размерность F счетно бесконечна. Стандартный базис состоит из векторов e i, которые содержат 1 в i-м слоте и нули в другом месте. Это векторное пространство является копроизведением (или прямой суммой ) счетного количества копий векторного пространства F.

Обратите внимание на роль условия конечности здесь. Можно рассматривать произвольные последовательности элементов в F, которые также составляют векторное пространство с теми же операциями, часто обозначаемыми F - см. ниже. F является произведением счетного числа копий F.

Согласно лемме Цорна, F имеет базис (очевидного базиса нет). В базе бесчисленное множество элементов. Поскольку размеры различны, F не изоморфен F. Стоит отметить, что F является (изоморфным) двойным пространством к F, потому что линейное отображение T из F в F определяется однозначно своими значениями T (e i) на основе элементов F, и эти значения могут быть произвольными. Таким образом, можно увидеть, что векторное пространство не обязательно должно быть изоморфным своему двойному двойному, если оно бесконечномерно, в отличие от конечномерного случая.

Начиная с n векторных пространств или их счетного бесконечного набора, каждое с одним и тем же полем, мы можем определить пространство произведения, как указано выше.

Пусть F обозначает набор m × n матриц с элементами из F. Тогда F - векторное пространство над F. Сложение векторов - это просто сложение матриц и скалярное умножение определяется очевидным образом (умножением каждой записи на один и тот же скаляр). Нулевой вектор - это просто нулевая матрица . Размер F равен mn. Один из возможных вариантов базиса - это матрицы с одним элементом, равным 1, а все остальные элементы - 0.

Когда m = n, матрица представляет собой квадрат и матричное умножение из двух таких матриц получается третья. Это векторное пространство размерности n образует алгебру над полем.

Одна переменная

Набор полиномов с коэффициентами в F равен векторное пространство над F, обозначаемое F [x]. Сложение векторов и скалярное умножение определяются очевидным образом. Если степень многочленов неограничена, то размерность F [x] равна счетно бесконечной. Если вместо этого ограничиться многочленами со степенью меньше или равной n, то мы получим векторное пространство с размерностью n + 1.

Одним из возможных базисов для F [x] является мономиальный базис : координаты многочлена относительно этого базиса - это его коэффициенты, а отображение, отправляющее многочлен в последовательность его коэффициентов, - это линейный изоморфизм от F [x] к бесконечное координатное пространство F.

Векторное пространство многочленов с действительными коэффициентами и степенью меньше или равной n часто обозначается как P n.

Несколько переменных

Набор многочлены от нескольких переменных с коэффициентами в F - это векторное пространство над F, обозначенное F [x 1, x 2,…, x r ]. Здесь r - количество переменных.

См. Также: Кольцо многочленов

См. Основную статью на Функциональное пространство, особенно раздел функционального анализа.

Пусть X будет непустым произвольным множеством и V - произвольное векторное пространство над F. Пространство всех функций от X до V является векторным пространством над F при поточечном сложении и умножении. То есть пусть f: X → V и g: X → V обозначают две функции, а α в F. Определим

$(f\; +\; g)\; (x)\; =\; f\; (x)\; +\; g\; (x)\; \{\backslash \; displaystyle\; (е\; +\; g)\; (x)\; =\; f\; (x)\; +\; g\; (x)\}$

$(\alpha \; f)\; (x)\; =\; \alpha \; f\; (x)\; \{\backslash \; displaystyle\; (\backslash \; alpha\; f)\; (x)\; =\; \backslash \; alpha\; f\; (x)\}$

где операции в правой части - операции в V. Нулевой вектор задается постоянной функцией, отправляющей все в нулевой вектор в V. Пространство всех функций от X до V обычно является обозначается V.

Если X конечно и V конечномерно, то V имеет размерность | X | (dim V), в противном случае пространство бесконечномерно (несчетное число, если X бесконечно).

Многие векторные пространства, возникающие в математике, являются подпространствами некоторого функционального пространства. Приведем еще несколько примеров.

Обобщенное координатное пространство

Пусть X - произвольный набор. Рассмотрим пространство всех функций от X до F, которые обращаются в нуль во всех, кроме конечного числа точек в X. Это пространство является векторным подпространством F, пространством всех возможных функций от X до F. Чтобы увидеть это, обратите внимание, что объединение двух конечных множеств конечно, так что сумма двух функций в этом пространстве все равно обращается в нуль вне конечного множества.

Описанное выше пространство обычно обозначается (F) 0 и называется обобщенным координатным пространством по следующей причине. Если X - это набор чисел от 1 до n, то это пространство, как легко видеть, эквивалентно координатному пространству F. Аналогично, если X - это набор натуральных чисел, N, то это пространство просто F.

Канонической основой для (F) 0 является набор функций {δ x | x ∈ X}, определяемый формулой

$\delta \; x\; (y)\; =\; \{1\; x\; =\; y\; 0\; x\; \ne \; y\; \{\backslash \; displaystyle\; \backslash \; delta\; \_\; \{x\}\; (y)\; =\; \{\backslash \; begin\; \{cases\}\; 1\; \backslash \; quad\; x\; =\; y\; \backslash \; \backslash \; 0\; \backslash \; quad\; x\; \backslash \; neq\; y\; \backslash \; end\; \{cases\}\}\}$

Следовательно, размерность (F) 0 равна мощности X. Таким образом, мы может построить векторное пространство любой размерности над любым полем. Кроме того, каждое векторное пространство изоморфно одному из этих видов. Любой выбор базиса определяет изоморфизм, переводя базис в канонический для (F) 0.

Обобщенное координатное пространство также можно понимать как прямую сумму | X | копии F (т.е. по одной для каждой точки в X):

$(F\; X)\; 0\; =\; ⨁\; x\; \in \; X\; F.\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{F\}\; ^\; \{X\})\; \_\; \{0\}\; =\; \backslash \; bigoplus\; \_\; \{x\; \backslash \; in\; X\}\; \backslash \; mathbf\; \{F\}.\}$

Условие конечности встроено в определение прямой суммы. Сравните это с прямым произведением | X | копии F, которые дали бы полное функциональное пространство F.

Линейные карты

Важным примером, возникающим в контексте самой линейной алгебры, является векторное пространство линейные карты. Пусть L (V, W) обозначает множество всех линейных отображений из V в W (оба из которых являются векторными пространствами над F). Тогда L (V, W) - подпространство в W, поскольку оно замкнуто относительно сложения и скалярного умножения.

Обратите внимание, что L (F, F) можно естественным образом отождествить с пространством матриц F. Фактически, выбирая подходящие базисы для конечномерных пространств V и W, L (V, W) также можно отождествить с F. Это отождествление обычно зависит от выбора базиса.

Непрерывные функции

Если X является некоторым топологическим пространством, например, единичным интервалом [0,1], мы можем рассматривать пространство все непрерывные функции от X до R . Это векторное подпространство в R, поскольку сумма любых двух непрерывных функций непрерывна, а скалярное умножение непрерывно.

Дифференциальные уравнения

Подмножество пространства всех функций от R до R, состоящее из (достаточно дифференцируемых) функций, которые удовлетворяют определенному дифференциальное уравнение является подпространством R, если уравнение является линейным. Это потому, что дифференцирование является линейной операцией, то есть (a f + b g) ′ = a f ′ + b g ′, где ′ - оператор дифференцирования.

Предположим, K - подполе из F (см. расширение поля ). Тогда F можно рассматривать как векторное пространство над K, ограничивая скалярное умножение элементами в K (сложение векторов определяется как нормальное). Размерность этого векторного пространства, если оно существует, называется степенью расширения. Например, комплексные числа Cобразуют двумерное векторное пространство над действительными числами R . Аналогично, действительные числа Rобразуют векторное пространство над рациональными числами Q, которое имеет (несчетное количество) бесконечную размерность, если существует базис Гамеля.

Если V - вектор пространство над F его также можно рассматривать как векторное пространство над K. Размеры связаны формулой

dim K V = (dim F V) (dim KF)

Например, C, рассматриваемое как векторное пространство над вещественными числами, имеет размерность 2n.

Помимо тривиального случая ноль- размерное пространство над любым полем, векторное пространство над полем F имеет конечное число элементов тогда и только тогда, когда F является конечным полем и векторное пространство имеет конечную размерность. Таким образом, мы имеем F q, единственное конечное поле (до изоморфизма ) с q элементами. Здесь q должно быть степенью простого числа (q = p с простым p). Тогда любое n-мерное векторное пространство V над F q будет иметь q элементов. Обратите внимание, что количество элементов в V также является степенью простого числа (поскольку власть первичной силы снова первичная сила). Основным примером такого пространства является координатное пространство (F q).

Эти векторные пространства имеют решающее значение в теории представлений конечных групп, теории чисел и криптографии.