Алгебра Хопфа

В математике, А алгебра Хопфа, названная в честь Heinz Хопфа, является структурой, которая является одновременно ( унитальным ассоциативной) алгебра и (counital coassociative) коалгебра, с совместимостью этих структур делают его биалгебру, и что, кроме того оснащено антиавтоморфизмом удовлетворяющие определенному свойству. Теория представлений алгебры Хопфа особенно хороша, поскольку существование совместимого коумножения, коэлита и антипода позволяет строить тензорные произведения представлений, тривиальных представлений и двойственных представлений.

Алгебры Хопфа естественным образом встречаются в алгебраической топологии, откуда они возникли и связаны с концепцией H-пространства, в теории схем групп, в теории групп (через концепцию группового кольца ) и во многих других местах, что делает их, вероятно, наиболее распространенными. знакомый тип биалгебры. Алгебры Хопфа также изучаются сами по себе, с большой работой над конкретными классами примеров, с одной стороны, и проблемами классификации, с другой. У них есть самые разные приложения, начиная от физики конденсированного состояния и квантовой теории поля до теории струн и феноменологии LHC.

• 1 Формальное определение
  • 1.1 Структурные константы
  • 1.2 Свойства антипода
  • 1.3 Подалгебры Хопфа
  • 1.4 Заказы Хопфа
  • 1.5 Групповые элементы
• 2 Примеры
  • 2.1 Когомологии групп Ли
  • 2.2 Квантовые группы и некоммутативная геометрия
• 3 Теория представлений
• 4 Понятия, связанные с данным
  • 4.1 Слабые алгебры Хопфа
  • 4.2 Алгеброиды Хопфа
• 5 Аналогия с группами
• 6 алгебры Хопфа в плетеных моноидальных категории
• 7 См. Также
• 8 Примечания и ссылки
  • 8.1 Примечания
  • 8.2 Ссылки

Формально алгебра Хопфа - это (ассоциативная и коассоциативная) биалгебра H над полем K вместе с K- линейным отображением S: H → H (называемым антиподом), такая что следующая диаграмма коммутирует :

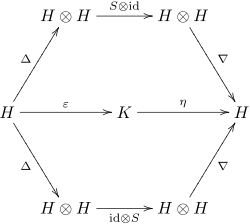
Здесь Δ - коумножение биалгебры, - ее умножение, η - ее единица, а ε - ее счетчик. В нотации Sumless Sweedler это свойство также может быть выражено как

${\ Displaystyle S (c _ {(1)}) c _ {(2)} = c _ {(1)} S (c _ {(2)}) = \ varepsilon (c) 1 \ qquad {\ t_dv {для всех} } c \ in H.}$

Что же касается алгебры, можно заменить, лежащий в основе поля K с коммутативным кольцом R в приведенном выше определении.

Определение алгебры Хопфа является самодвойственным (что отражено в симметрии вышеприведенной диаграммы), поэтому, если можно определить двойственное к H (что всегда возможно, если H конечномерно), то это автоматически алгебра Хопфа..

Структурные константы

Зафиксировав основу для лежащего в основе векторного пространства, можно определить алгебру в терминах структурных констант для умножения: ${\ Displaystyle \ {е_ {к} \}}$

${\ displaystyle e_ {i} \ nabla e_ {j} = \ sum _ {k} \ mu _ {\; ij} ^ {k} e_ {k}}$

для совместного умножения:

${\ displaystyle \ Delta e_ {i} = \ sum _ {j, k} \ nu _ {i} ^ {\; jk} e_ {j} \ otimes e_ {k}}$

и антипод:

${\ displaystyle Se_ {i} = \ sum _ {j} \ tau _ {i} ^ {\; j} e_ {j}}$

Тогда ассоциативность требует, чтобы

${\ displaystyle \ mu _ {\; ij} ^ {k} \ mu _ {\; kn} ^ {m} = \ mu _ {\; jn} ^ {k} \ mu _ {\; ik} ^ { m}}$

в то время как соассоциативность требует, чтобы

${\ displaystyle \ nu _ {k} ^ {\; ij} \ nu _ {i} ^ {\; mn} = \ nu _ {k} ^ {\; mi} \ nu _ {i} ^ {\; nj}}$

Связующая аксиома требует, чтобы

${\ displaystyle \ nu _ {k} ^ {\; ij} \ tau _ {j} ^ {\; m} \ mu _ {\; pm} ^ {n} = \ nu _ {k} ^ {\; jm} \ tau _ {j} ^ {\, \; i} \ mu _ {\; pm} ^ {n}}$

Свойства антипода

Антиподом S иногда требуется, чтобы иметь K -линейные обратный, который является автоматическим в конечномерном случае, или если Н является коммутативным или кокоммутативен (или в более общем случае квазитреугольном ).

В общем, S является антигомоморфизмом, поэтому S ² является гомоморфизмом, который, следовательно, является автоморфизмом, если S был обратимым (что может потребоваться).

Если S ² = id H, то алгебра Хопфа называется инволютивной (а основная алгебра с инволюцией является * -алгеброй ). Если H конечномерно полупросто над полем нулевой характеристики, коммутативно или кокоммутативно, то оно инволютивно.

Если биалгебра B допускает антипод S, то S единственна («биалгебра допускает не более 1 структуры алгебры Хопфа»). Таким образом, антипод не создает никакой дополнительной структуры, которую мы можем выбрать: быть алгеброй Хопфа - это свойство биалгебры.

Антипод является аналогом отображения инверсии на группе, которое переводит g в g ⁻¹.

Подалгебры Хопфа

Подалгебру из алгебры Хопфа H подалгебра Хопфа, если это subcoalgebra из H и антипод S отображает A в A. Другими словами, подалгебра Хопфа A является алгеброй Хопфа сама по себе, когда умножение, коумножение, коумножение и антипод H ограничены до A (и, кроме того, тождество 1 H требуется, чтобы находиться в A). Теорема Николса – Зеллера о свободе установила (в 1989 г.), что естественный A- модуль H не имеет конечного ранга, если H конечномерно: это обобщение теоремы Лагранжа для подгрупп. Как следствие этой и интегральной теории, подалгебра Хопфа полупростой конечномерной алгебры Хопфа автоматически полупроста.

Подалгебра Хопфа A называется нормальной справа в алгебре Хопфа H, если она удовлетворяет условию устойчивости ad r ( h) ( A) ⊆ A для всех h в H, где правое сопряженное отображение ad r определяется формулой ad г ( ч) () = S ( ч (1)) ах (2) для всех а в А, ч в H. Точно так же подалгебра Хопфа A остается нормальной в H, если она устойчива относительно сопряженного слева отображения, заданного формулой ad l ( h) ( a) = h (1) aS ( h (2)). Два условия нормальности эквивалентны, если антипод S биективен, и в этом случае A называется нормальной подалгеброй Хопфа.

Нормальная подалгебра Хопфа в H удовлетворяет условию (равенства подмножеств H): HA ⁺ = ⁺Н, где ⁺ обозначает ядро коединицы на K. Из этого условия нормальности следует, что HA ⁺ - идеал Хопфа в H (т. Е. Идеал алгебры в ядре коединицы, коидеальная и устойчивая коалгебра относительно антипода). Как следствие, возникает фактор-алгебра Хопфа H / HA ⁺ и эпиморфизм H → H / A ⁺H, теория, аналогичная теории нормальных подгрупп и фактор-групп в теории групп.

Заказы Хопфа

Хопфа порядок вывода над областью целостности R с полем частных K представляет собой порядок в алгебре Хопфа H над K, который закрыт под алгебры и коалгебра операций: в частности, коумножение Δ отображает вывода для вывода ⊗ вывода.

Групповые элементы

Группы, как элемент является ненулевым элементом х таким образом, что Δ ( х) = х ⊗ х. Группоподобные элементы образуют группу с инверсией, задаваемой антиподом. Для примитивного элемента x выполняется Δ ( x) = x ⊗1 + 1⊗ x.

	В зависимости от	Умножение	Графство	Антипод	Коммутативный	Кокоммутативный	Замечания
групповая алгебра KG	группа G	Δ ( g) = g ⊗ g для всех g в G	ε ( g) = 1 для всех g в G	S ( g) = g −1 для всех g в G	тогда и только тогда, когда G абелева	да
функции f из конечной группы в K, K G (с поточечным сложением и умножением)	конечная группа G	Δ ( f) ( x, y) = f ( xy)	ε ( f) = f (1 г)	S ( е) ( х) = е ( х - 1)	да	тогда и только тогда, когда G абелева
Представительные функции на компактной группе	компактная группа G	Δ ( f) ( x, y) = f ( xy)	ε ( f) = f (1 г)	S ( е) ( х) = е ( х - 1)	да	тогда и только тогда, когда G абелева	Наоборот, всякая коммутативная инволютивная редуцированная алгебра Хопфа над C с конечным интегралом Хаара возникает таким образом, что дает одну формулировку двойственности Таннаки – Крейна.
Регулярные функции на алгебраической группе		Δ ( f) ( x, y) = f ( xy)	ε ( f) = f (1 г)	S ( е) ( х) = е ( х - 1)	да	тогда и только тогда, когда G абелева	Наоборот, всякая коммутативная алгебра Хопфа над полем возникает из групповой схемы таким образом, что дает антиэквивалентность категорий.
Тензорная алгебра T ( V)	векторное пространство V	Δ ( x) = x ⊗ 1 + 1 ⊗ x, x в V, Δ (1) = 1 ⊗ 1	ε ( х) = 0	S ( x) = - x для всех x в 'T 1 ( V) (и расширен до более высоких тензорных степеней)	Если и только если dim ( V) = 0,1	да	симметрическая алгебра и внешняя алгебра (которые являются факторами тензорной алгебры) также являются алгебрами Хопфа с таким определением коумножения, коединицы и антипода.
Универсальная обертывающая алгебра U (g)	Алгебра Ли g	Δ ( x) = x ⊗ 1 + 1 ⊗ x для каждого x в g (это правило совместимо с коммутаторами и, следовательно, может быть однозначно распространено на все U)	ε ( x) = 0 для всех x в g (опять же, продолжено на U)	S ( х) = - х	тогда и только тогда, когда g абелева	да
Алгебра Хопфа Свидлера H = K [ c, x ] / c 2 = 1, x 2 = 0 и xc = - cx.	K - поле с характеристикой, отличной от 2	Δ ( c) = c ⊗ c, Δ ( x) = c ⊗ x + x ⊗ 1, Δ (1) = 1 ⊗ 1	ε ( c) = 1 и ε ( x) = 0	S ( c) = c −1 = c и S ( x) = - cx	нет	нет	Основное векторное пространство порождается {1, c, x, cx } и, таким образом, имеет размерность 4. Это наименьший пример алгебры Хопфа, которая одновременно некоммутативна и некокоммутативна.
кольцо симметричных функций		через полные однородные симметричные функции h k ( k ≥ 1): Δ ( ч к) знак равно 1 ⊗ ч К + ч 1 ⊗ ч к −1 +... + ч к −1 ⊗ ч 1 + ч к ⊗ 1.	ε ( h k) = 0	S ( h k) = (−1) k e k	да	да

Обратите внимание, что функции на конечной группе можно отождествить с групповым кольцом, хотя их более естественно рассматривать как двойственные - групповое кольцо состоит из конечных сумм элементов и, таким образом, соединяется с функциями на группе, вычисляя функцию на суммированном элементы.

Когомологии групп Ли

Алгебра когомологий (над полем) группы Ли - это алгебра Хопфа: умножение обеспечивается чашечным произведением, а коумножение ${\ displaystyle K}$${\ displaystyle G}$

${\ displaystyle H ^ {*} (G, K) \ rightarrow H ^ {*} (G \ times G, K) \ cong H ^ {*} (G, K) \ otimes H ^ {*} (G, K)}$

групповым умножением. Это наблюдение было фактически источником понятия алгебры Хопфа. Используя эту структуру, Хопф доказал структурную теорему для алгебры когомологий групп Ли. ${\ displaystyle G \ times G \ to G}$

Теорема (Хопф) Пусть - конечномерная градуированная коммутативная градуированная кокоммутативная алгебра Хопфа над полем характеристики 0. Тогда (как алгебра) является свободной внешней алгеброй с образующими нечетной степени. ${\ displaystyle A}$ ${\ displaystyle A}$

Квантовые группы и некоммутативная геометрия

Основная статья: квантовая группа

Все приведенные выше примеры либо коммутативны (т. Е. Умножение коммутативно ), либо ко-коммутативно (т. Е. Δ = T ∘ Δ, где твист-отображение T: H ⊗ H → H ⊗ H определяется формулой T ( x ⊗ y) = y ⊗ x). Другими интересными алгебрами Хопфа являются определенные «деформации» или « квантования » алгебр из примера 3, которые не являются ни коммутативными, ни ко-коммутативными. Эти алгебры Хопфа часто называют квантовыми группами, термин, который до сих пор определяется нечетко. Они важны в некоммутативной геометрии, идея заключается в следующем: стандартная алгебраическая группа хорошо описывается своей стандартной алгеброй Хопфа регулярных функций; тогда мы можем думать о деформированной версии этой алгебры Хопфа как о некой «нестандартной» или «квантованной» алгебраической группе (которая вообще не является алгебраической группой). Хотя кажется, что нет прямого способа определять или манипулировать этими нестандартными объектами, можно по-прежнему работать с их алгебрами Хопфа и действительно отождествлять их с их алгебрами Хопфа. Отсюда и название «квантовая группа».

Пусть A - алгебра Хопфа, а M и N - A -модули. Тогда M ⊗ N также является A -модулем, причем

${\ displaystyle a (m \ otimes n): = \ Delta (a) (m \ otimes n) = (a_ {1} \ otimes a_ {2}) (m \ otimes n) = (a_ {1} m \ иногда a_ {2} n)}$

для m ∈ M, n ∈ N и ∆ ( a) = ( a 1, a 2). Кроме того, мы можем определить тривиальное представление как базовое поле K с

${\ Displaystyle а (м): = \ эпсилон (а) м}$

для м ∈ K. Наконец, можно определить двойственное представление A: если M - A -модуль, а M * - его двойственное пространство, то

${\ Displaystyle (аф) (т): = е (S (а) м)}$

где F ∈ M * и т ∈ M.

Связь между Δ, ε и S гарантирует, что некоторые естественные гомоморфизмы векторных пространств действительно являются гомоморфизмами A -модулей. Например, естественные изоморфизмы векторных пространств M → M ⊗ K и M → K ⊗ M также являются изоморфизмами A -модулей. Кроме того, отображение векторных пространств M * ⊗ M → K с f ⊗ m → f ( m) также является гомоморфизмом A -модулей. Однако отображение M ⊗ M * → K не обязательно является гомоморфизмом A -модулей.

Градуированные алгебры Хопфа часто используются в алгебраической топологии : они представляют собой естественную алгебраическую структуру на прямой сумме всех групп гомологий или когомологий H-пространства.

Локально компактные квантовые группы обобщают алгебры Хопфа и несут топологию. Алгебра всех непрерывных функций на группе Ли является локально компактной квантовой группой.

Квазихопфовые алгебры являются обобщениями алгебр Хопфа, где коассоциативность сохраняется только с точностью до твиста. Они были использованы при изучении уравнений Книжника – Замолодчикова.

Алгебры мультипликаторов Хопфа, введенные Альфонсом Ван Даэлем в 1994 году, являются обобщениями алгебр Хопфа, в которых коумножение алгебры (с единицей или без нее) на алгебру мультипликаторов тензорной алгебры произведения алгебры с самим собой.

Групповые (ко) алгебры Хопфа, введенные В. Г. Тураевым в 2000 г., также являются обобщениями алгебр Хопфа.

Слабые алгебры Хопфа

Слабые алгебры Хопфа или квантовые группоиды являются обобщениями алгебр Хопфа. Подобно алгебрам Хопфа, слабые алгебры Хопфа образуют самодуальный класс алгебр; т. е. если H - (слабая) алгебра Хопфа, то H * - двойственное пространство линейных форм на H (по отношению к структуре алгебры-коалгебры, полученной естественным спариванием с H и ее структурой коалгебры-алгебры). Слабая алгебра Хопфа H обычно считается

• конечномерна алгебра и коалгебра с копроизведением А: Н → Н ⊗ Н и коединица amp; epsi ;: H → K, удовлетворяющий все аксиомами алгебры Хопфа, за исключением, возможно, Д (1) ≠ 1 ⊗ 1 или е ( абы) ≠ ε () amp; epsi ; ( б) для некоторых а, Ь в Н. Вместо этого требуется следующее:

${\ Displaystyle (\ Delta (1) \ otimes 1) (1 \ otimes \ Delta (1)) = (1 \ otimes \ Delta (1)) (\ Delta (1) \ otimes 1) = (\ Delta \ otimes {\ t_dv {Id}}) \ Delta (1)}$

${\ displaystyle \ epsilon (abc) = \ sum \ epsilon (ab _ {(1)}) \ epsilon (b _ {(2)} c) = \ sum \ epsilon (ab _ {(2)}) \ epsilon (b_ { (1)} c)}$

для всех в, б, и с в Н.

• H имеет ослабленный антипод S: H → H, удовлетворяющий аксиомам:

1. ${\ Displaystyle S (а _ {(1)}) а _ {(2)} = 1 _ {(1)} \ epsilon (a1 _ {(2)})}$для всех a в H (правая часть представляет собой интересную проекцию, обычно обозначаемую Π ^R ( a) или ε s ( a) с изображением сепарабельной подалгебры, обозначаемой H ^R или H s);
2. ${\ Displaystyle а _ {(1)} S (а _ {(2)}) = \ epsilon (1 _ {(1)} а) 1 _ {(2)}}$для всех a в H (другая интересная проекция, обычно обозначаемая как Π ^R ( a) или ε t ( a), образ которой является сепарабельной алгеброй H ^L или H t, антиизоморфной H ^L посредством S);
3. ${\ Displaystyle S (а _ {(1)}) а _ {(2)} S (а _ {(3)}) = S (а)}$для всех а в H.

Заметим, что если ∆ (1) = 1 ⊗ 1, эти условия сводятся к двум обычным условиям на антипод алгебры Хопфа.

Частично аксиомы выбраны так, что категория H -модулей является жесткой моноидальной категорией. Единичный H -модуль - это упомянутая выше сепарабельная алгебра H ^L.

Например, алгебра конечных группоидов является слабой алгеброй Хопфа. В частности, группоидом алгебра на [N] с одной парой обратима стрелки е IJ и е ц между I и J в [ п ] изоморфна алгебре Н из п х п матриц. Структура слабой алгебры Хопфа на этой конкретной H задается копроизведением ∆ ( e ij) = e ij ⊗ e ij, countit ε ( e ij) = 1 и антиподом S ( e ij) = e ji. Сепарабельные подалгебры H ^L и H ^R совпадают и в данном частном случае являются нецентральными коммутативными алгебрами (подалгеброй диагональных матриц).

Ранние теоретические вклады в слабые алгебры Хопфа можно найти, а также в

Алгеброиды Хопфа

См. Алгеброид Хопфа

Группы могут быть аксиоматизированы с помощью тех же диаграмм (то есть операций), что и алгебра Хопфа, где G рассматривается как множество, а не модуль. В этом случае:

• поле K заменяется одноточечным множеством
• есть естественная страна (сопоставить с 1 точкой)
• есть естественное коумножение (диагональное отображение)
• единица является тождественным элементом группы
• умножение - это умножение в группе
• антипод обратный

В этой философии группу можно рассматривать как алгебру Хопфа над « полем с одним элементом ».

Определение алгебры Хопфа естественным образом распространяется на произвольные сплетенные моноидальные категории. Алгебра Хопфа в такой категории - это шестерка, в которой - объект, а ${\ displaystyle (C, \ otimes, I, \ alpha, \ lambda, \ rho, \ gamma)}$${\ Displaystyle (Н, \ набла, \ эта, \ Дельта, \ varepsilon, S)}$${\ displaystyle H}$${\ displaystyle C}$

${\ displaystyle \ nabla: H \ otimes H \ to H}$ (умножение),

${\ displaystyle \ eta: от I \ до H}$ (Ед. изм),

${\ displaystyle \ Delta: H \ to H \ otimes H}$ (коумножение),

${\ displaystyle \ varepsilon: H \ to I}$ (счет),

${\ displaystyle S: H \ to H}$ (антипод)

- морфизмы в такие, что ${\ displaystyle C}$

1) тройка является моноидом в моноидальной категории, т. Е. Следующие диаграммы коммутативны:${\ displaystyle (H, \ nabla, \ eta)}$ ${\ displaystyle (C, \ otimes, I, \ alpha, \ lambda, \ rho, \ gamma)}$

2) тройка является комоноидом в моноидальной категории, т. Е. Следующие диаграммы коммутативны:${\ displaystyle (H, \ Delta, \ varepsilon)}$ ${\ displaystyle (C, \ otimes, I, \ alpha, \ lambda, \ rho, \ gamma)}$

3) структуры моноида и комоноида на совместимы: умножение и единица являются морфизмами комоноидов, и (в данной ситуации это эквивалентно) в то же время коумножение и коумножение являются морфизмами моноидов; это означает, что следующие диаграммы должны быть коммутативными:${\ displaystyle H}$${\ displaystyle \ nabla}$${\ displaystyle \ eta}$${\ displaystyle \ Delta}$${\ displaystyle \ varepsilon}$

пятерка со свойствами 1), 2), 3) называется биалгеброй в категории ;${\ Displaystyle (Н, \ набла, \ эта, \ Дельта, \ varepsilon)}$${\ displaystyle (C, \ otimes, I, \ alpha, \ lambda, \ rho, \ gamma)}$

4) диаграмма антипода коммутативна:

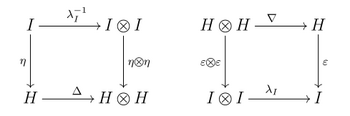
Типичные примеры следующие.

• Группы. В моноидальной категории из множеств (с декартово произведением как тензорное произведение, и произвольным singletone, скажем, в качестве единичного объекта) тройкой является моноидом в категориальной смысле тогда и только тогда, когда она является моноидом в обычном алгебраическом смысл, т.е. если операции и ведут себя как обычное умножение и единица в (но, возможно, без обратимости элементов). В то же время тройка является комоноидом в категориальном смысле тогда и только тогда, когда это диагональная операция (и операция также определена однозначно:). И любая такая структура комоноида совместима с любой структурой моноида в том смысле, что диаграммы в разделе 3 определения всегда коммутируют. Как следствие, каждый моноид in естественно рассматривать как биалгебру в, и наоборот. Существование антипода для такой биалгебры в точности означает, что каждый элемент имеет обратный элемент по отношению к умножению. Таким образом, в категории множеств алгебры Хопфа - это в точности группы в обычном алгебраическом смысле.${\ displaystyle ({\ text {Set}}, \ times, 1)}$ ${\ displaystyle \ times}$${\ displaystyle 1 = \ {\ varnothing \}}$${\ displaystyle (H, \ nabla, \ eta)}$ ${\ Displaystyle \ набла (х, у) = х \ CDOT у}$${\ displaystyle \ eta (1)}$${\ displaystyle H}$${\ displaystyle x \ in H}$${\ displaystyle (H, \ Delta, \ varepsilon)}$${\ displaystyle \ Delta}$${\ Displaystyle \ Delta (х) = (х, х)}$${\ displaystyle \ varepsilon}$${\ Displaystyle \ varepsilon (х) = 1}$${\ displaystyle (H, \ Delta, \ varepsilon)}$${\ displaystyle (H, \ nabla, \ eta)}$${\ displaystyle (H, \ nabla, \ eta)}$${\ displaystyle ({\ text {Set}}, \ times, 1)}$${\ Displaystyle (Н, \ набла, \ эта, \ Дельта, \ varepsilon)}$${\ displaystyle ({\ text {Set}}, \ times, 1)}$${\ displaystyle S: H \ to H}$${\ Displaystyle (Н, \ набла, \ эта, \ Дельта, \ varepsilon)}$${\ displaystyle x \ in H}$${\ displaystyle x ^ {- 1} \ in H}$${\ Displaystyle \ набла (х, у) = х \ CDOT у}$${\ displaystyle ({\ text {Set}}, \ times, 1)}$
• Классические алгебры Хопфа. В частном случае, когда - категория векторных пространств над данным полем, алгебры Хопфа в являются в точности классическими алгебрами Хопфа, описанными выше.${\ displaystyle (C, \ otimes, s, I)}$${\ displaystyle K}$${\ displaystyle (C, \ otimes, s, I)}$
• Функциональные алгебры на группах. Стандартные функциональные алгебры,,, (непрерывный, гладкие, голоморфные, регулярные функции) на группах являются алгебрами Хопфа в категории ( Ste,) из стереотипных пространств,${\ Displaystyle {\ mathcal {C}} (G)}$${\ Displaystyle {\ mathcal {E}} (G)}$${\ Displaystyle {\ mathcal {O}} (G)}$${\ Displaystyle {\ mathcal {P}} (G)}$${\ displaystyle \ odot}$
• Групповые алгебры. В алгебрах стереотипа группы,,, (меры, распределение, аналитические функционалы и токов) на группах являются алгебрами Хопфа в категории ( Ste,) из стереотипных пространств. Эти алгебры Хопфа используются в теориях двойственности для некоммутативных групп. ${\ Displaystyle {\ mathcal {C}} ^ {\ звезда} (G)}$${\ displaystyle {\ mathcal {E}} ^ {\ star} (G)}$${\ Displaystyle {\ mathcal {O}} ^ {\ звезда} (G)}$${\ Displaystyle {\ mathcal {P}} ^ {\ star} (G)}$${\ displaystyle \ circledast}$

• Квазитреугольная алгебра Хопфа
• Алгебра / аналогия множеств
• Теория представлений алгебр Хопфа
• Ленточная алгебра Хопфа
• Супералгебра
• Супергруппа
• Аньонная алгебра Ли
• Алгебра Свидлера Хопфа
• Алгебра перестановок Хопфа
• Теорема Милнора – Мура

Примечания

использованная литература

• Дэскэлеску, Сорин; Нэстэсеску, Константин; Райану, Щербан (2001), Алгебры Хопфа. Введение, Чистая и прикладная математика, 235 (1-е изд.), Марсель Деккер, ISBN   978-0-8247-0481-0, Zbl   0962,16026.
• Картье, Пьер (2007), «Учебник по алгебрам Хопфа», в Cartier, P.; Moussa, P.; Юлия, Б.; Vanhove, П. (ред.), Frontiers в теории чисел, физики и геометрии, II, Берлин: Springer, С. 537-615,. DOI : 10.1007 / 978-3-540-30308-4_12, ISBN   978-3-540-30307-7
• Фукс, Юрген (1992), аффинные алгебры Ли и квантовые группы. Введение с приложениями в конформной теории поля, Кембриджские монографии по математической физике, Кембридж: Cambridge University Press, ISBN   978-0-521-48412-1, Zbl   0925,17031
• Хайнц Хопф, Uber die Topologie der Gruppen-Mannigfaltigkeiten und ihrer Verallgemeinerungen, Annals of Mathematics 42 (1941), 22–52. Перепечатано в Selecta Heinz Hopf, pp. 119–151, Springer, Berlin (1964). Руководство по ремонту 4784, Zbl   0025.09303
• Монтгомери, Сьюзен (1993), алгебры Хопфа и их действия на кольцах, Серия региональных конференций по математике, 82, Провиденс, Род-Айленд: Американское математическое общество, ISBN   978-0-8218-0738-5, Zbl   0793,16029
• Стрит, Росс (2007), Квантовые группы: путь к современной алгебре, Серия лекций Австралийского математического общества, 19, Cambridge University Press, ISBN   978-0-521-69524-4, Руководство по ремонту   2294803, Zbl   1117.16031.
• Свидлер, Мосс Э. (1969), алгебры Хопфа, серия лекций по математике, WA Benjamin, Inc., Нью-Йорк, ISBN   9780805392548, MR   0252485, Zbl   0194.32901
• Андервуд, Роберт Г. (2011), Введение в алгебры Хопфа, Берлин: Springer-Verlag, ISBN   978-0-387-72765-3, Zbl   1234,16022
• Тураев, Владимир; Вирелизье, Алексис (2017), Моноидальные категории и топологическая теория поля, Прогресс в математике, 322, Springer, DOI : 10.1007 / 978-3-319-49834-8, ISBN   978-3-319-49833-1.
• Акбаров, С.С. (2003). «Двойственность Понтрягина в теории топологических векторных пространств и в топологической алгебре». Журнал математических наук. 113 (2): 179–349. DOI : 10,1023 / А: 1020929201133. S2CID   115297067.
• Акбаров, С.С. (2009). «Голоморфные функции экспоненциального типа и двойственности для групп Штейна с алгебраической связной компонентой единицы». Журнал математических наук. 162 (4): 459–586. arXiv : 0806.3205. DOI : 10.1007 / s10958-009-9646-1. S2CID   115153766.