Полилогарифм

В математике полилогарифм (также известная как функция Жонкьера по имени Альфреда Жонкьера) - это специальная функция Lis(z) порядка s и аргумента z. Только для специальных значений s полилогарифм сводится к элементарной функции , такой как натуральный логарифм или рациональные функции. В квантовой статистике функция полилогарифма появляется как замкнутая форма интегралов от распределения Ферми – Дирака и распределения Бозе – Эйнштейна, и также известен как интеграл Ферми – Дирака или интеграл Бозе – Эйнштейна . В квантовой электродинамике полилогарифмы положительного целого порядка возникают при вычислении процессов, представленных диаграммами Фейнмана более высокого порядка .

Функция полилогарифма эквивалентна Дзета-функция Гурвица - любая функция может быть выражена через другую - и обе функции являются частными случаями трансцендента Лерха. Полилогарифмы не следует путать с полилогарифмическими функциями или с логарифмическим интегралом смещения, который имеет ту же запись, но с одной переменной.

• Различные функции полилогарифма в комплексной плоскости
• 

  Li−3(z)

• 

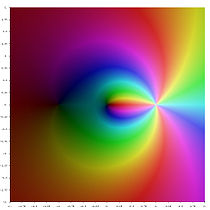
  Li−2(z)

• 

  Li−1(z)

• 

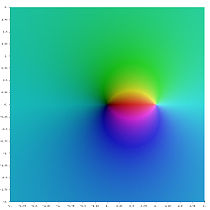
  Li0(z)

• 

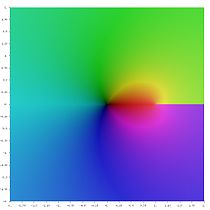
  Li1(z)

• 

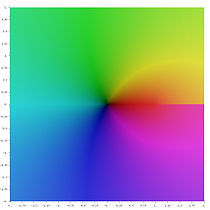
  Li2(z)

• 

  Li3( z)

Функция полилогарифма определяется степенным рядом по z, который также является рядом Дирихле по s:

$Li\; s\; \; (z)\; =\; \sum \; k\; Знак\; равно\; 1\; \infty \; zkks\; знак\; равно\; z\; +\; z\; 2\; 2\; s\; +\; z\; 3\; 3\; s\; +\; \cdots \; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{z\; ^\; \{k\}\; \backslash \; over\; k\; ^\; \{s\}\}\; =\; z\; +\; \{z\; ^\; \{2\}\; \backslash \; over\; 2\; ^\; \{s\}\}\; +\; \{z\; ^\; \{3\}\; \backslash \; over\; 3\; ^\; \{s\}\}\; +\; \backslash \; cdots\}$

Это определение действительно для произвольного комплексного порядка s и для всех комплексных аргументов z с | z | <1; его можно продолжить до | z | ≥ 1 в процессе аналитического продолжения. В частном случае s = 1 используется обычный натуральный логарифм, Li 1 (z) = −ln (1 − z), а в частных случаях s = 2 и s = 3 называется дилогарифмом (также называемым функцией Спенса) и трилогарифмом соответственно. Название функции связано с тем, что ее также можно определить как повторяющийся интеграл самого себя:

$Li\; s\; +\; 1\; \; (z)\; =\; \int \; 0\; z\; Li\; s\; \; (t)\; tdt\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\; +\; 1\}\; (z)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{z\}\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (t)\}\; \{t\}\}\; dt\; \}$

таким образом дилогарифм является интегралом функции, содержащей логарифм, и так далее. Для неположительных целочисленных порядков s полилогарифм является рациональной функцией.

• 1 Свойства
• 2 Частные значения
• 3 Связь с другими функциями
• 4 Интегральные представления
• 5 Последовательные представления
• 6 Асимптотические расширения
• 7 Ограничивающее поведение
• 8 Дилогарифм
• 9 Полилогарифм лестницы
• 10 Монодромия
• 11 Ссылки
• 12 Внешние ссылки

В случай, когда порядок полилогарифмов $s\; \{\backslash \; displaystyle\; s\}$является целым числом, он будет представлен как $n\; \{\backslash \; displaystyle\; n\}$(или $-\; n\; \{\backslash \; displaystyle\; -n\}$в случае отрицательного значения). Часто бывает удобно определить $\mu \; =\; пер\; \; (z)\; \{\backslash \; displaystyle\; \backslash \; mu\; =\; \backslash \; ln\; (z)\}$где $ln\; \; (z)\; \{\backslash \; displaystyle\; \backslash \; ln\; (z)\}$- главная ветвь комплексного логарифма $Ln\; \; (z)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Ln\}\; (z)\}$, так что Также предполагается, что все возведения в степень однозначны: $zs\; =\; exp\; \; (s\; ln\; \; (z)).\; \{\backslash \; displaystyle\; z\; ^\; \{s\}\; =\; \backslash \; exp\; (s\; \backslash \; ln\; (z)).\}$

В зависимости от порядка $s\; \{\backslash \; displaystyle\; s\}$полилогарифм может быть многозначным. ценится. Основная ветвь $Li\; s\; \; (z)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\}$считается заданной для в соответствии с приведенным выше определением серии и считается непрерывным, за исключением положительной действительной оси, где выполняется разрез от $z\; =\; 1\; \{\backslash \; displaystyle\; z\; =\; 1\}$до $\infty \; \{\backslash \; displaystyle\; \backslash \; infty\}$таким образом, чтобы ось размещалась в нижней полуплоскости $z\; \{\backslash \; displaystyle\; z\}$. В терминах $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$это составляет . Прерывистость полилогарифма в зависимости от $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$иногда может сбивать с толку.

Для вещественного аргумента $z\; \{\backslash \; displaystyle\; z\}$полилогарифм действительного порядка $s\; \{\backslash \; displaystyle\; s\}$является действительным, если , а его мнимая часть для $z\; \ge \; 1\; \{\backslash \; displaystyle\; z\; \backslash \; geq\; 1\}$равна (Wood 1992, § 3):

$Im\; \; (Li\; s\; \; (z))\; =\; -\; \pi \; \mu \; s\; -\; 1\; \Gamma \; (s).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Im\}\; \backslash \; left\; (\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; \backslash \; right)\; =\; -\; \{\{\backslash \; pi\; \backslash \; mu\; ^\; \{s-1\}\}\; \backslash \; over\; \{\backslash \; Gamma\; (s)\}\; \}.\}$

Если пересечь разрез, если ε бесконечно малое положительное вещественное число, то:

$Im\; \; (Li\; s\; \; (z\; +\; i\; ϵ))\; =\; \pi \; \mu \; s\; -\; 1\; \Gamma \; (s).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Im\}\; \backslash \; left\; (\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z\; +\; i\; \backslash \; epsilon)\; \backslash \; right)\; =\; \{\{\backslash \; pi\; \backslash \; mu\; ^\; \{s-1\}\}\; \backslash \; over\; \{\backslash \; Gamma\; (\; s)\}\}.\}$

Оба могут быть заключены из разложения в ряд (см. ниже) Li s (e) о μ = 0.

Производные полилогарифма следуют из определяющего степенного ряда:

$z\; \partial \; Li\; s\; \; (z)\; \partial \; z\; =\; Li\; s\; -\; 1\; \; (z)\; \{\backslash \; displaystyle\; z\; \{\backslash \; partial\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; \backslash \; over\; \backslash \; partial\; z\}\; =\; \backslash \; operatorname\; \{Li\}\; \_\; \{s-1\}\; (z)\}$

$\partial \; Li\; s\; \; (e\; \mu )\; \partial \; \mu \; =\; Li\; s\; -\; 1\; \; (e\; \mu ).\; \{\backslash \; displaystyle\; \{\backslash \; partial\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; \backslash \; over\; \backslash \; partial\; \backslash \; mu\}\; =\; \backslash \; operatorname\; \{Li\}\; \_\; \{s-1\}\; (e\; ^\; \{\backslash \; mu\}).\}$

Отношение квадратов видно из определения ряда и связано с формулой дублирования (см. Также Clunie (1954), Schrödinger (1952)):

$Li\; s\; \; (-\; z)\; +\; Li\; s\; \; (z)\; =\; 2\; 1\; -\; s\; Li\; s\; \; (z\; 2).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; z)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; 2\; ^\; \{1-s\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z\; ^\; \{\; 2\}).\}$

Функция Куммера подчиняется очень похожей формуле дублирования. Это частный случай формулы умножения для любого целого положительного числа p:

$\sum \; m\; =\; 0\; p\; -\; 1\; Li\; s\; \; (ze\; 2\; \pi \; im\; /\; p)\; =\; p\; 1\; -\; s\; Li\; s\; \; (zp),\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{m\; =\; 0\}\; ^\; \{p-1\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (ze\; ^\; \{2\; \backslash \; pi\; im\; /\; p\})\; =\; p\; ^\; \{1-s\; \}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z\; ^\; \{p\}),\}$

что может быть доказано, используя определение полилогарифма рядами и ортогональность экспоненциальных членов (см., например, дискретное преобразование Фурье ).

Другое важное свойство, формула обращения, включает в себя дзета-функцию Гурвица или полиномы Бернулли и находится в связи с другими функциями ниже..

Для особых случаев полилогарифм может быть выражен в терминах других функций (см. Ниже). Таким образом, конкретные значения полилогарифма также могут быть найдены как конкретные значения этих других функций.

1.Для целочисленных значений порядка полилогарифма следующие явные выражения получаются повторным применением z · ∂ / ∂z к Li 1 (z):

$Li\; 1\; \; (z)\; =\; -\; пер\; \; (1\; -\; z)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{1\}\; (z)\; =\; -\; \backslash \; ln\; (1-z)\}$

$Li\; 0\; \; (z)\; =\; z\; 1\; -\; z\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{0\}\; (z)\; =\; \{z\; \backslash \; over\; 1-z\}\}$

$Li\; -\; 1\; \; (z)\; =\; z\; (1\; -\; z)\; 2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{\; -1\}\; (z)\; =\; \{z\; \backslash \; over\; (1-z)\; ^\; \{2\}\}\}$

$Li\; -\; 2\; \; (z)\; =\; z\; (1\; +\; z)\; (1\; -\; z)\; 3\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; 2\}\; (z)\; =\; \{z\; (1\; +\; z)\; \backslash \; over\; (1-z)\; ^\; \{3\}\}\}$

$Li\; -\; 3\; \; (z)\; =\; z\; (1\; +\; 4\; z\; +\; z\; 2)\; (1\; -\; z)\; 4\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; 3\}\; (z)\; =\; \{z\; (1\; +\; 4z\; +\; z\; ^\; \{2\})\; \backslash \; over\; (1-z)\; ^\; \{4\}\; \}\}$

$Li\; -\; 4\; \; (z)\; =\; z\; (1\; +\; z)\; (1\; +\; 10\; z\; +\; z\; 2)\; (1\; -\; z)\; 5.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; 4\}\; (z)\; =\; \{z\; (1\; +\; z)\; (1\; +\; 10z\; +\; z\; ^\; \{2\})\; \backslash \; over\; (1-z)\; ^\; \{5\}\}.\}$

Соответственно, полилогарифм сводится к соотношению многочленов по z и, следовательно, является рациональной функцией от z для всех неположительных целочисленных порядков. Общий случай можно представить в виде конечной суммы:

$Li\; -\; n\; \; (z)\; =\; (z\; \partial \; \partial \; z)\; n\; z\; 1\; -\; z\; =\; \sum \; k\; =\; 0\; n\; k!\; S\; (N\; +\; 1,\; К\; +\; 1)\; (Z\; 1\; -\; Z)\; К\; +\; 1\; (N\; =\; 0,\; 1,\; 2,\dots ),\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{-\; n\}\; (z)\; =\; \backslash \; left\; (z\; \{\backslash \; partial\; \backslash \; over\; \backslash \; partial\; z\}\; \backslash \; right)\; ^\; \{n\}\; \{z\; \backslash \; over\; \{1-z\}\}\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; k!\; S\; (n\; +\; 1,\; k\; +1)\; \backslash \; left\; (\{z\; \backslash \; over\; \{1-z\}\}\; \backslash \; right)\; ^\; \{k\; +\; 1\}\; \backslash \; qquad\; (n\; =\; 0,1,2,\; \backslash \; ldots),\}$

где S (n, k) являются числами Стирлинга второго рода. Эквивалентные формулы, применимые к отрицательным целым порядкам, следующие (Wood 1992, § 6):

$Li\; -\; n\; \; (z)\; =\; (-\; 1)\; n\; +\; 1\; \sum \; k\; =\; 0\; n\; k!\; S\; (N\; +\; 1,\; к\; +\; 1)\; (-\; 1\; 1\; -\; z)\; k\; +\; 1\; (n\; =\; 1,\; 2,\; 3,\dots ),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; n\}\; (z)\; =\; (\; -1)\; ^\; \{n\; +\; 1\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; k!\; S\; (n\; +\; 1,\; k\; +\; 1)\; \backslash \; left\; (\{\{-\; 1\}\; \backslash \; over\; \{1-z\}\}\; \backslash \; справа)\; ^\; \{k\; +\; 1\}\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots),\}$

и:

$Li\; -\; n\; \; (z)\; =\; 1\; (1\; -\; z)\; n\; +\; 1\; \sum \; К\; знак\; равно\; 0\; N\; -\; 1\; ⟨NK⟩\; Zn\; -\; К\; (N\; =\; 1,\; 2,\; 3,\dots ),\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{-\; п\}\; (г)\; =\; \{1\; \backslash \; над\; (1-г)\; ^\; \{n\; +\; 1\}\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n-1\}\; \backslash \; left\; \backslash \; langle\; \{n\; \backslash \; atop\; k\}\; \backslash \; right\; \backslash \; rangle\; z\; ^\; \{nk\}\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots),\}$

где $⟨nk⟩\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; left\; \backslash \; langle\; \{n\; \backslash \; atop\; k\}\; \backslash \; right\; \backslash \; rangle\}$- числа Эйлера. Все корни Li −n (z) различны и действительны; они включают z = 0, а остаток отрицателен и центрируется вокруг z = -1 в логарифмической шкале. По мере того как n становится большим, численная оценка этих рациональных выражений все больше страдает от аннулирования (Wood 1992, § 6); однако полная точность может быть получена путем вычисления Li -n (z) через общую связь с дзета-функцией Гурвица (см. ниже).

2.Некоторые конкретные выражения для полуцелых значений аргумента z:

$Li\; 1\; \; (1\; 2)\; =\; ln\; \; 2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{1\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; \backslash \; ln\; 2\}$

$Li\; 2\; \; (1\; 2)\; =\; 1\; 12\; \pi \; 2\; -\; 1\; 2\; (ln\; \; 2)\; 2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; \{\backslash \; tfrac\; \{1\}\; \{12\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (\backslash \; ln\; 2)\; ^\; \{2\}\}$

$Ли\; 3\; \; (1\; 2)\; знак\; равно\; 1\; 6\; (пер\; 2)\; 3\; -\; 1\; 12\; \pi \; 2\; пер\; 2\; +\; 7\; 8\; \zeta \; (3),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{3\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; \{\backslash \; tfrac\; \{1\}\; \{6\}\}\; (\backslash \; ln\; 2)\; ^\; \{3\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{12\}\}\; \backslash \; pi\; ^\; \{2\}\; \backslash \; ln\; 2\; +\; \{\backslash \; tfrac\; \{\; 7\}\; \{8\}\}\; \backslash \; zeta\; (3),\}$

где ζ - дзета-функция Римана. Формулы этого типа для высших целочисленных порядков неизвестны (Lewin 1991, p. 2), но есть, например, (Borwein, Borwein Girgensohn 1995):

$Li\; 4\; \; (1\; 2)\; знак\; равно\; 1360\; \pi \; 4-1\; 24\; (пер\; \; 2)\; 4\; +\; 1\; 24\; \pi \; 2\; (пер\; \; 2)\; 2-1\; 2\; \zeta \; (3\; ¯,\; 1\; ¯),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\; \}\; \_\; \{4\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; \{\backslash \; tfrac\; \{1\}\; \{360\}\}\; \backslash \; pi\; ^\; \{4\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{24\}\}\; (\backslash \; ln\; 2)\; ^\; \{4\}\; +\; \{\backslash \; tfrac\; \{1\}\; \{24\}\}\; \backslash \; pi\; ^\; \{2\}\; (\backslash \; ln\; 2)\; ^\; \{2\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; zeta\; (\{\backslash \; bar\; \{3\}\; \},\; \{\backslash \; bar\; \{1\}\}),\}$

который включает в себя двойную переменную сумму

$\zeta \; (3\; ¯,\; 1\; ¯)\; =\; \sum \; m>n>0\; (-\; 1)\; m\; +\; nm\; -\; 3\; n\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; zeta\; (\{\backslash \; bar\; \{3\}\},\; \{\backslash \; bar\; \{1\}\})\; =\; \backslash \; sum\; \_\; \{m>n>0\}\; (-\; 1)\; ^\; \{m\; +\; n\}\; m\; ^\; \{-\; 3\}\; n\; ^\; \{-\; 1\}.\}$

Как правило, для целочисленных порядков n ≥ 2 (Broadhurst 1996, стр. 9):

$Li\; n\; \; (1\; 2)\; =\; -\; \zeta \; (1\; ¯,\; 1\; ¯,\; \{1\}\; n\; -\; 2),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; -\; \backslash \; zeta\; (\{\backslash \; bar\; \{1\}\},\; \{\backslash \; bar\; \{1\}\},\; \backslash \; left\; \backslash \; \{1\; \backslash \; right\; \backslash \}\; ^\; \{n-2\}),\; \}$

где ζ (s 1,..., s k) - это множественная дзета-функция ; например:

$Li\; 5\; \; (1\; 2)\; =\; -\; \zeta \; (1\; ¯,\; 1\; ¯,\; 1,\; 1,\; 1).\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{5\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; -\; \backslash \; zeta\; (\; \{\backslash \; bar\; \{1\}\},\; \{\backslash \; bar\; \{1\}\},\; 1,1,1).\}$

3.Как непосредственное следствие определения ряда, значения полилогарифма в p-м комплексном корнях из единицы задаются суммой Фурье :

$Li\; s\; \; (e\; 2\; \pi \; im\; /\; p)\; =\; p\; -\; s\; \sum \; k\; =\; 1\; pe\; 2\; \pi \; imk\; /\; p\; \zeta \; (s,\; kp)\; (m\; =\; 1,\; 2,\dots ,\; p\; -\; 1),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{2\; \backslash \; pi\; im\; /\; p\})\; =\; p\; ^\; \{-\; s\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{p\}\; e\; ^\; \{2\; \backslash \; pi\; imk\; /\; p\}\; \backslash \; zeta\; (s,\; \{\backslash \; tfrac\; \{k\}\; \{p\}\})\; \backslash \; qquad\; (m\; =\; 1,2,\; \backslash \; точки,\; p-1),\}$

где ζ - дзета-функция Гурвица. Для Re (s)>1, где Li s (1) конечно, соотношение также выполняется при m = 0 или m = p. Хотя эта формула не так проста, как это подразумевается более общей связью с дзета-функцией Гурвица, перечисленной в разделе отношение к другим функциям ниже, ее преимущество также заключается в применении к неотрицательным целым значениям s.. Как обычно, отношение можно инвертировать, чтобы выразить ζ (s, ⁄ p) для любого m = 1,..., p как сумму Фурье Li s (exp ( 2πi ⁄ p)) над k = 1,..., p.

• Для z = 1 полилогарифм сводится к дзета-функции Римана

$Li\; s\; \; (1)\; =\; \zeta \; (s)\; (Re\; \; (s)>1).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (1)\; =\; \backslash \; zeta\; (s)\; \backslash \; qquad\; (\backslash \; operatorname\; \{Re\}\; (s)>1).\}$

• Полилогарифм связан с Dir функция эта и бета-функция Дирихле :

$Li\; s\; \; (-\; 1)\; =\; -\; \eta \; (s),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; 1)\; =\; -\; \backslash \; eta\; (s),\}$

где η (s) - эта функция Дирихле. Для чисто мнимых аргументов имеем:

$Li\; s\; \; (\pm \; i)\; =\; -\; 2\; -\; s\; \eta \; (s)\; \pm \; i\; \beta \; (\; s),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (\backslash \; pm\; i)\; =\; -\; 2\; ^\; \{-\; s\}\; \backslash \; eta\; (s)\; \backslash \; pm\; i\; \backslash \; beta\; (s),\}$

где β (s) является бета-функцией Дирихле.

• Полилогарифм связан с полным интегралом Ферми – Дирака как:

$F\; s\; (\mu )\; =\; -\; Li\; s\; +\; 1\; \; (-\; e\; \mu ).\; \{\backslash \; displaystyle\; F\_\; \{s\}\; (\backslash \; mu)\; =\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\; +\; 1\}\; (-\; e\; ^\; \{\backslash \; mu\}).\}$

• Полилогарифм является частным случаем неполного полилогарифм функция

$Li\; s\; \; (z)\; =\; Li\; s\; \; (0,\; z).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (0,\; z).\}$

• Полилогарифм является частным случаем трансцендента Лерха (Erdélyi et al. 1981, § 1.11-14)

$Li\; s\; \; (z)\; =\; z\; \Phi \; (z,\; s,\; 1).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; z\; \backslash \; Phi\; (z,\; s,\; 1).\}$

• Полилогарифм связан с дзета-функцией Гурвица следующим соотношением:

$Li\; s\; \; (z)\; =\; \Gamma \; (1\; -\; s)\; (2\; \pi )\; 1\; -\; s\; [i\; 1\; -\; s\; \zeta \; (1\; -\; s,\; 1\; 2\; +\; ln\; \; (-\; z)\; 2\; \pi \; i)\; +\; is\; -\; 1\; \zeta \; (1\; -\; s,\; 1\; 2\; -\; пер\; \; (-\; z)\; 2\; \pi \; я)],\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\backslash \; Gamma\; (1-s)\; \backslash \; over\; (2\; \backslash \; pi)\; ^\; \{1-s\}\}\; \backslash \; left\; [i\; ^\; \{1-s\}\; \backslash \; zeta\; \backslash \; left\; (1-s,\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; +\; \{\backslash \; ln\; (-z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right)\; +\; i\; ^\; \{s-1\}\; ~\; \backslash \; zeta\; \backslash \; left\; (1-s,\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \{\backslash \; ln\; (-z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\; \}\}\; \backslash \; right)\; \backslash \; right],\}$

это отношение, однако, недействительно при положительном целом числе s полюсами гамма-функции Γ (1-s), и при s = 0 полюсом обеих дзета-функций; вывод этой формулы приведен ниже в разделе серийные представления. С небольшой помощью функционального уравнения для дзета-функции Гурвица полилогарифм, следовательно, также связан с этой функцией через (Jonquière 1889):

$i\; -\; s\; Li\; s\; \; (e\; 2\; \pi \; ix)\; +\; is\; Li\; s\; \; (е\; -\; 2\; \pi \; ix)\; знак\; равно\; (2\; \pi )\; s\; \Gamma \; (s)\; \zeta \; (1\; -\; s,\; x),\; \{\backslash \; displaystyle\; i\; ^\; \{-\; s\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{2\; \backslash \; pi\; ix\})\; +\; i\; ^\; \{s\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{-\; 2\; \backslash \; pi\; ix\})\; =\; \{(2\; \backslash \; pi)\; ^\; \{s\}\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; \backslash \; zeta\; (1-s,\; x),\}$

, которое выполняется при 0 ≤ Re (x) < 1 if Im(x) ≥ 0, and for 0 < Re(x) ≤ 1 if Im(x) < 0. Equivalently, for all complex s and for complex z ∉ ]0;1], the inversion formula reads

$Li\; s\; \; (z)\; +\; (-\; 1)\; s\; Li\; s\; \; (1\; /\; z)\; =\; (2\; \pi \; я)\; s\; \Gamma \; (s)\; \zeta \; (1\; -\; s,\; 1\; 2\; +\; ln\; \; (-\; z)\; 2\; \pi \; я),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; +\; (-\; 1)\; ^\; \{s\; \}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (1\; /\; z)\; =\; \{(2\; \backslash \; pi\; i)\; ^\; \{s\}\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; ~\; \backslash \; zeta\; \backslash \; left\; (1-s,\; ~\; \{\backslash \; frac\; \{\; 1\}\; \{2\}\}\; +\; \{\backslash \; ln\; (-z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right),\}$

и для всех комплексных s и для комплексных z ∉] 1; ∞ [

$Li\; s\; \; (z)\; +\; (-\; 1)\; s\; Li\; s\; \; (1\; /\; z)\; =\; (2\; \pi \; i)\; s\; \Gamma \; (s)\; \zeta \; (1\; -\; s,\; 1\; 2\; -\; ln\; \; (-\; 1\; /\; z)\; 2\; \pi \; i)).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; +\; (-\; 1)\; ^\; \{s\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (1\; /\; z)\; =\; \{(2\; \backslash \; pi\; i)\; ^\; \{\; s\}\; \backslash \; ov\; er\; \backslash \; Gamma\; (s)\}\; ~\; \backslash \; zeta\; \backslash \; left\; (1-s,\; ~\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \{\backslash \; ln\; (-1\; /\; z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right).\}$

Для z ∉] 0; ∞ [ln (−z) = −ln (−⁄ z), и оба выражения согласуются. Эти соотношения дают аналитическое продолжение полилогарифма за круг сходимости | z | = 1 определяющего степенного ряда. (Соответствующее уравнение Jonquière (1889, уравнение 5) и Erdélyi et al. (1981, § 1.11-16) неверно, если предположить, что основные ветви Полилогарифм и логарифм используются одновременно.) См. следующий пункт для упрощенной формулы, когда s является целым числом.

• Для положительных целых порядков полилогарифма s дзета-функция Гурвица ζ (1 - s, x) сокращается до Многочлены Бернулли, ζ (1 − n, x) = −B n (x) / n, и формула обращения Жонкьера для n = 1, 2, 3,... принимает следующий вид:

$Li\; N\; \; (e\; 2\; \pi \; ix)\; +\; (-\; 1)\; n\; Li\; n\; \; (e\; -\; 2\; \pi \; ix)\; =\; -\; (2\; \pi \; i)\; nn!\; В\; N\; (Икс),\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{n\}\; (e\; ^\; \{2\; \backslash \; pi\; ix\})\; +\; (-\; 1)\; ^\; \{n\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (e\; ^\; \{\; -2\; \backslash \; pi\; ix\})\; =\; -\; \{(2\; \backslash \; pi\; i)\; ^\; \{n\}\; \backslash \; over\; n!\}\; B\_\; \{n\}\; (x),\}$

где снова 0 ≤ Re (x) < 1 if Im(x) ≥ 0, and 0 < Re(x) ≤ 1 if Im(x) < 0. Upon restriction of the polylogarithm argument to the unit circle, Im(x) = 0, the left hand side of this formula simplifies to 2 Re(Lin(e)), если n четное, и 2i Im (Li n (e)), если n нечетное. С другой стороны, для отрицательных целых порядков дивергенция Γ (s) означает, что для всех z (Erdélyi et al. 1981, § 1.11-17):

$Li\; -\; n\; \; (z)\; +\; (-\; 1)\; n\; Li\; -\; n\; \; (1\; /\; z)\; =\; 0\; (n\; =\; 1,\; 2,\; 3,\dots ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; n\}\; (z)\; +\; (-\; 1)\; ^\; \{n\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; n\}\; (1\; /\; z)\; =\; 0\; \backslash \; qquad\; (n\; =\; 1,2,\; 3,\; \backslash \; ldots).\}$

В более общем случае для n = 0, ± 1, ± 2, ± 3,...:

$Li\; n\; \; (z)\; +\; (-\; 1)\; n\; Li\; n\; \; (1\; /\; z)\; знак\; равно\; -\; (2\; \pi \; я)\; nn!\; В\; N\; (1\; 2\; +\; пер\; \; (-\; z)\; 2\; \pi \; я)\; (z\; \notin ]\; 0;\; 1]),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (z)\; +\; (-\; 1)\; ^\; \{n\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (1\; /\; z)\; =\; -\; \{\backslash \; frac\; \{(2\; \backslash \; pi\; i)\; ^\; \{n\}\}\; \{n!\}\}\; B\_\; \{n\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\; 2\}\}\; +\; \{\backslash \; ln\; (-z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right)\; \backslash \; qquad\; (z\; \backslash \; not\; \backslash \; in]\; 0;\; 1]),\}$

$Li\; n\; \; (z)\; +\; (\; -\; 1)\; N\; Li\; N\; \; (1\; /\; z)\; знак\; равно\; -\; (2\; \pi \; я)\; nn!\; В\; N\; (1\; 2\; -\; пер\; \; (-\; 1\; /\; z)\; 2\; \pi \; я)\; (z\; \notin ]\; 1;\; \infty \; [),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (z)\; +\; (-\; 1)\; ^\; \{\; n\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (1\; /\; z)\; =\; -\; \{\backslash \; frac\; \{(2\; \backslash \; pi\; i)\; ^\; \{n\}\}\; \{n!\}\}\; B\_\; \{n\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\; \}\; \{2\}\}\; -\; \{\backslash \; ln\; (-1\; /\; z)\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right)\; \backslash \; qquad\; (z\; \backslash \; not\; \backslash \; in\; ~]\; 1;\; \backslash \; infty\; [),\}$

где оба выражения согласуются при z ∉] 0; ∞ [. (Соответствующее уравнение Jonquière (1889, уравнение 1) и Erdélyi et al. (1981, § 1.11-18) снова неверно.)

• Полилогарифм с чисто мнимое μ может быть выражено через функции Клаузена Cis(θ) и Si s (θ), и наоборот (Lewin 1958, Ch. VII § 1.4; Abramowitz Stegun 1972, § 27.8):

$Li\; s\; \; (e\; \pm \; i\; \theta )\; =\; C\; is\; (\theta )\; \pm \; i\; S\; is\; (\theta ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; pm\; i\; \backslash \; theta\})\; =\; Ci\_\; \{s\}\; (\backslash \; theta)\; \backslash \; pm\; iSi\_\; \{s\}\; (\backslash \; theta).\}$

• The интеграл обратной касательной Tis(z) (Lewin 1958, Ch. VII § 1.2) может быть выражен в терминах полилогарифмов:

$Ti\; s\; \; (z)\; =\; 1\; 2\; i\; [Li\; s\; \; (iz)\; -\; Li\; s\; \; (-\; iz)].\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Ti\}\; \_\; \{s\}\; (z)\; =\; \{1\; \backslash \; over\; 2i\}\; \backslash \; left\; [\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (iz)\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; iz)\; \backslash \; right].\}$

Это соотношение, в частности, подразумевает:

$Ti\; 0\; \; (z)\; =\; z\; 1\; +\; z\; 2,\; Ti\; 1\; \; (z)\; =\; arctan\; \; z,\; Ti\; 2\; \; (z)\; =\; \int \; 0\; z\; arctan\; \; ttdt,\dots \; Ti\; n\; +\; 1\; \; (z)\; =\; \int \; 0\; z\; Ti\; n\; \; (t)\; tdt,\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Ti\}\; \_\; \{0\}\; (z)\; =\; \{z\; \backslash \; over\; 1\; +\; z\; ^\; \{2\}\},\; \backslash \; quad\; \backslash \; operatorname\; \{Ti\}\; \_\; \{1\}\; (z)\; =\; \backslash \; arctan\; z,\; \backslash \; quad\; \backslash \; operatorname\; \{Ti\}\; \_\; \{2\}\; (z)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{z\}\; \{\backslash \; arctan\; t\; \backslash \; over\; t\}\; dt,\; \backslash \; quad\; \backslash \; ldots\; ~\; \backslash \; quad\; \backslash \; operatorname\; \{Ti\}\; \_\; \{n\; +\; 1\}\; (z)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{z\}\; \{\backslash \; frac\; \{\backslash \; operatorname\{Ti\}\; \_\; \{n\}\; (t)\}\; \{t\}\}\; dt,\}$

, в котором объясняется имя функции.

• Функция ци Лежандра χs(z) (Левин 1958, Ch. VII § 1.1; Boersma Dempsey 1992) можно выразить в терминах полилогарифмов:

$\chi \; s\; (z)\; =\; 1\; 2\; [Li\; s\; \; (z)\; -\; Li\; s\; (-\; z)].\; \{\backslash \; displaystyle\; \backslash \; chi\; \_\; \{s\}\; (z)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; left\; [\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; z)\; \backslash \; right].\}$

• Полилогарифм целого порядка может быть выражен как обобщенная гипергеометрическая функция :

$Li\; n\; \; (z)\; =\; zn\; +\; 1\; F\; n\; (1,\; 1,\dots ,\; 1;\; 2,\; 2,\dots ,\; 2;\; z)\; (n\; =\; 0,\; 1,\; 2,\dots ),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (z)\; =\; z\_\; \{n\; +\; 1\}\; F\_\; \{n\}\; (1,\; 1,\; \backslash \; dots,\; 1;\; 2,2,\; \backslash \; dots,\; 2;\; z)\; \backslash \; qquad\; (n\; =\; 0,1,2,\; \backslash \; ldots),\}$

$Li\; -\; n\; \; (z)\; =\; zn\; F\; n\; -\; 1\; (2,\; 2,\dots ,\; 2;\; 1,\; 1,\dots ,\; 1;\; z)\; (n\; =\; 1,\; 2,\; 3,\dots ).\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{-\; n\}\; (z)\; =\; z\_\; \{n\}\; F\_\; \{n-1\}\; (2,2,\; \backslash \; точки,\; 2;\; 1,1,\; \backslash \; точки,\; 1;\; z)\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots)\; ~.\}$

• В терминах неполных дзета-функций или «функций Дебая » (Abramowitz Stegun 1972, § 27.1):

$Z\; n\; (z)\; =\; 1\; (n\; -\; 1)!\; \int \; z\; \infty \; tn\; -\; 1\; et\; -\; 1\; dt\; (n\; =\; 1,\; 2,\; 3,\dots ),\; \{\backslash \; displaystyle\; Z\_\; \{n\}\; (z)\; =\; \{1\; \backslash \; over\; (n-1)!\}\; \backslash \; Int\; \_\; \{z\}\; ^\; \{\backslash \; infty\}\; \{t\; ^\; \{n-1\}\; \backslash \; over\; e\; ^\; \{t\}\; -1\}\; dt\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots),\}$

полилогарифм Li n (z) для положительного целого числа n может быть выражено как конечная сумма (Wood 1992, § 16):

$Li\; n\; \; (e\; \mu )\; =\; \sum \; k\; =\; 0\; n\; -\; 1\; Z\; п\; -\; к\; (-\; \mu )\; \mu \; кк!\; (n\; =\; 1,\; 2,\; 3,\dots ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{n\}\; (e\; ^\; \{\backslash \; mu\})\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n-1\}\; Z\_\; \{nk\}\; (-\; \backslash \; mu)\; \{\backslash \; mu\; ^\; \{k\; \}\; \backslash \; over\; k!\}\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots).\}$

Замечательно похожее выражение связывает "функции Дебая" Z n (z) с полилогарифмом:

$Z\; n\; (z)\; знак\; равно\; \sum \; k\; знак\; равно\; 0\; n\; -\; 1\; Li\; n\; -\; k\; \; (e\; -\; z)\; zkk!\; (n\; =\; 1,\; 2,\; 3,\dots ).\; \{\backslash \; displaystyle\; Z\_\; \{n\}\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n-1\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{nk\}\; (e\; ^\; \{-\; z\})\; \{z\; ^\; \{k\}\; \backslash \; over\; k!\}\; \backslash \; qquad\; (n\; =\; 1,2,3,\; \backslash \; ldots).\}$

Любое из следующих интегральных представлений обеспечивает аналитическое продолжение полилогарифма за пределы круг сходимости | z | = 1 определяющего степенного ряда.

1.Полилогарифм может быть выражен через интеграл от распределения Бозе - Эйнштейна :

$Li\; s\; \; (z)\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; t\; s\; -\; 1\; e\; t\; /\; z\; -\; 1\; d\; t.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{1\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{t\; ^\; \{s-1\}\; \backslash \; over\; e\; ^\; \{\; t\}\; /\; z-1\}\; dt.\}$

Это будет для Re (s)>0 и всех z, кроме вещественных z и ≥ 1. Полилогарифм в этом контексте иногда называют интегралом Бозе, но чаще как а. Точно так же полилогарифм можно выразить через интеграл от распределения Ферми - Дирака :

$-\; Li\; s\; \; (-\; z)\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; ts\; -\; 1\; et\; /\; z\; +\; 1\; dt.\; \{\backslash \; displaystyle\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; z)\; =\; \{1\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{t\; ^\; \{s-1\}\; \backslash \; over\; e\; ^\; \{t\}\; /\; z\; +\; 1\}\; dt.\}$

Это сходится для Re (s)>0 и всех z, кроме вещественного z и ≤ −1. Полилогарифм в этом контексте иногда называют интегралом Ферми или интегралом Ферми - Дирака (GSL 2010). Эти представления легко проверить с помощью разложения Тейлора подынтегрального выражения по z и почленного интегрирования. В работах Дингла подробные исследования обоих типов интегралов.

Полилогарифм также связан с интегралом от распределения Максвелла - Больцмана :

$lim\; z\; \to \; 0\; Li\; s\; \; (z)\; z\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; ts\; -\; 1\; e\; -\; tdt\; =\; 1.\; \{\backslash \; Displaystyle\; \backslash \; lim\; \_\; \{z\; \backslash \; to\; 0\}\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\}\; \{z\}\}\; =\; \{1\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; \backslash \; int\; \_\; \{0\; \}\; ^\; \{\backslash \; infty\}\; \{t\; ^\; \{s-1\}\; e\; ^\; \{-\; t\}\}\; dt\; =\; 1.\}$

Это также дает асимптотическое поведение полилогарифма в окрестностях происхождения.

2.Дополнительное интегральное представление к Re (s) < 0 and to all z except to z real and ≥ 0:

$Li\; s\; \; (z)\; =\; \int \; 0\; \infty \; t\; -\; s\; sin\; \; [s\; \pi \; /\; 2\; -\; t\; ln\; \; (-\; z)]\; sinh\; \; (\pi \; t)\; dt.\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{t\; ^\; \{-\; s\}\; \backslash \; sin\; [s\; \backslash \; pi\; /\; 2-t\; \backslash \; ln\; (-z)\; ]\; \backslash \; over\; \backslash \; sinh\; (\backslash \; pi\; t)\}\; dt.\}$

Этот интеграл следует из общей связи полилогарифма с дзета-функцией Гурвица (см. выше) и знакомое интегральное представление последнего.

3.Полилогарифм в общем виде может быть представлен в виде контура Ганкеля интеграла (Whittaker Watson 1927, § 12.22, § 13.13), который расширяет представление Бозе - Эйнштейна до отрицательных порядков. с. Пока t = μ полюс подынтегрального выражения не лежит на неотрицательной действительной оси и s ≠ 1, 2, 3,..., мы имеем:

$Li\; s\; \; (е\; \mu )\; знак\; равно\; -\; \Gamma \; (\; 1\; -\; s)\; 2\; \pi \; я\; \oint \; H\; (-\; t)\; s\; -\; 1\; et\; -\; \mu \; -\; 1\; dt\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; -\; \{\{\backslash \; Gamma\; (1\; -s)\}\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; oint\; \_\; \{H\}\; \{\{(-\; t)\; ^\; \{s-1\}\}\; \backslash \; over\; \{e\; ^\; \{t-\; \backslash \; mu\}\; -1\}\}\; dt\}$

где H представляет контур Ганкеля. Подынтегральная функция имеет разрез по действительной оси от нуля до бесконечности, причем ось принадлежит нижней полуплоскости t. Интегрирование начинается в + ∞ в верхней полуплоскости (Im (t)>0), обходит начало координат, не охватывая ни один из полюсов t = µ + 2kπi, и заканчивается в + ∞ в нижней полуплоскости (Im (t) < 0). For the case where µ is real and non-negative, we can simply subtract the contribution of the enclosed t = µ pole:

$Li\; s\; \; (е\; \mu )\; знак\; равно\; -\; \Gamma \; (1\; -\; s)\; 2\; \pi \; я\; \oint \; H\; \; (-\; t)\; s\; -\; 1\; et\; -\; \mu \; -\; 1\; dt\; -\; 2\; \pi \; i\; R\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; -\; \{\{\backslash \; Gamma\; (1-s)\}\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; oint\; \_\; \{H\}\; \{\{(-\; t)\; ^\; \{s-1\}\}\; \backslash \; over\; \{e\; ^\; \{t-\; \backslash \; mu\}\}\; -\; 1\}\; dt-2\; \backslash \; pi\; iR\}$

где R - остаток полюса:

$R\; =\; i\; 2\; \pi \; \Gamma \; (1\; -\; s)\; (\; -\; \mu )\; s\; -\; 1.\; \{\backslash \; Displaystyle\; R\; =\; \{i\; \backslash \; over\; 2\; \backslash \; pi\}\; \backslash \; Gamma\; (1-s)\; (-\; \backslash \; mu)\; ^\; \{s-1\}.\}$

4.Когда формула Абеля - Плана используемый к определяющему ряду полилогарифма, получается интегральное представление типа Эрмита, которое действительно для всех комплексных z и для всех сложных s:

$Li\; s\; \; (z)\; =\; 1\; 2\; z\; +\; \Gamma \; (\; 1\; -\; s,\; -\; ln\; \; z)\; (-\; ln\; \; z)\; 1\; -\; s\; +\; 2\; z\; \int \; 0\; \infty \; sin\; \; (s\; arctan\; \; t\; -\; t\; ln\; \; z)\; (1\; +\; T\; 2)\; s\; /\; 2\; (е\; 2\; \pi \; т\; -\; 1)\; dt\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\; \backslash \; tfrac\; \{1\}\; \{2\}\}\; z\; +\; \{\backslash \; Gamma\; (1-с,\; -\; \backslash \; ln\; z)\; \backslash \; over\; (-\; \backslash \; ln\; z)\; ^\; \{1-s\}\}\; +\; 2z\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; sin\; (s\; \backslash \; arctan\; tt\; \backslash \; ln\; z)\}\; \{(1\; +\; t\; ^\; \{2\})\; ^\; \{s\; /\; 2\}\; (e\; ^\; \{2\; \backslash \; pi\; t\}\; -1)\}\}\; dt\}$

где Γ - верхняя неполная гамма-функция. Все (но не часть) ln (z) в этом выражении можно заменить на −ln (⁄ z). Родственное представление, которое также верно для всех комплексных s,

$Li\; s\; \; (z)\; =\; 1\; 2\; z\; +\; z\; \int \; 0\; \infty \; sin\; \; [s\; arctan\; \; t\; -\; t\; ln\; \; (-\; z)]\; (1\; +\; t\; 2)\; s\; /\; 2\; зп\; \; (\pi \; t)\; dt,\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; z\; +\; z\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; sin\; [s\; \backslash \; arctan\; tt\; \backslash \; ln\; (-z)]\}\; \{(1\; +\; t\; ^\; \{2\})\; ^\; \{s\; /\; 2\}\; \backslash \; sinh\; (\backslash \; pi\; t)\}\}\; dt,\}$

избегает использования неполной гамма-функции, но интеграл не работает для z на положительной действительной оси, если Re (s) ≤ 0. Это выражение находится путем записи 2 Li s (−z) / (- z) = Φ (z, s, ⁄ 2) - z Φ (z, s, 1), где Φ - трансцендент Лерха, и применяя метод Абеля - Плана формулу к первому Ряду Φ и дополнительную формулу, которая включает 1 / (e + 1) вместо 1 / (e - 1) ко второму ряду Φ.

5. Как указано в, мы можем выразить интеграл для полилогарифма, интегрируя обычный геометрический ряд почленно для $s\; \in \; N\; \{\backslash \; displaystyle\; s\; \backslash \; in\; \backslash \; mathbb\; \{N\}\}$как

$Li\; s\; +\; 1\; \; (z)\; =\; z\; \cdot \; (-\; 1)\; ss!\; \int \; 0\; 1\; журнал\; s\; \; (t)\; 1\; -\; t\; z\; d\; t.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\; +\; 1\}\; (z)\; =\; \{\backslash \; frac\; \{z\; \backslash \; cdot\; (-1)\; ^\; \{s\}\}\; \{s!\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\; \backslash \; frac\; \{\backslash \; log\; ^\; \{s\}\; (t)\}\; \{1-tz\}\}\; dt.\}$

1., как отмечалось выше в разделе интегральные представления, интегральное представление Бозе - Эйнштейна полилогарифм может быть расширен до отрицательных порядков s посредством интегрирования контура Ганкеля :

$Li\; s\; \; (e\; \mu )\; =\; -\; \Gamma \; (1\; -\; s)\; 2\; \pi \; i\; \oint \; H\; (-\; t)\; s\; -\; 1\; et\; -\; \mu \; -\; 1\; dt,\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; -\; \{\backslash \; Gamma\; (1-s)\; \backslash \; over\; 2\; \backslash \; pi\; i\}\; \backslash \; oint\; \_\; \{H\}\; \{(\; -\; t)\; ^\; \{s-1\}\; \backslash \; over\; e\; ^\; \{t-\; \backslash \; mu\}\; -1\}\; dt,\}$

где H - контур Ганкеля, s ≠ 1, 2, 3,..., а полюс t = μ подынтегрального выражения не лежит на неотрицательной оси. Контур можно изменить так, чтобы он охватывал полюса подынтегрального выражения при t - µ = 2kπi, а интеграл можно вычислить как сумму остатков (Вуд 1992, § 12, 13; Градштейн и Рыжик 1980, § 9.553 ошибка harvnb: нет цели: CITEREF Li s ⁡ (e μ) = Γ (1 - s) ∑ k = - ∞ ∞ (2 к π я - μ) s - 1. {\ Displaystyle \ operatorname {Li} _ {s} (e ^ {\ mu}) = \ Gamma (1-s) \ sum _ {k = - \ infty} ^ { \ infty} (2k \ pi i- \ mu) ^ {s-1}.}

Это будет справедливо для Re (s) < 0 and all μ except where e = 1. For 0 < Im(µ) ≤ 2π the sum can be split as:

$Li\; s\; \; (e\; \mu )\; =\; \Gamma \; (1\; -\; s)\; [(\; -\; 2\; \pi \; i)\; s\; -\; 1\; \sum \; k\; Знак\; равно\; 0\; \infty \; (К\; +\; \mu \; 2\; \pi \; я)\; s\; -\; 1\; +\; (2\; \pi \; я)\; s\; -\; 1\; \sum \; К\; =\; 0\; \infty \; (к\; +\; 1\; -\; \mu \; 2\; \pi \; я)\; s\; -\; 1],\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; \backslash \; Gamma\; (1-s)\; \backslash \; left\; [(-\; 2\; \backslash \; pi\; i)\; ^\; \{s-1\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (k\; +\; \{\backslash \; mu\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right)\; ^\; \{s-1\}\; +\; (2\; \backslash \; pi\; i)\; ^\; \{s-1\}\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (k\; +\; 1\; -\; \{\backslash \; mu\; \backslash \; over\; \{2\; \backslash \; pi\; i\}\}\; \backslash \; right)\; ^\; \{s-1\}\; \backslash \; right],\}$

где две серии теперь можно идентифицирова ть с помощью Дзета-функция Гурвица :

Это соотношение, которое уже было указано в связи с другими функциями выше, выполнено для всех комплексных s ≠ 0, 1, 2, 3,... и впервые был получен в (Jonquière 1889, уравнение 6).

2.Чтобы представить полилогарифм в виде степенного ряда около µ = 0, запишем ряд, полученный из контурного интеграла Ганкеля, как:

$Li\; s\; \; (e\; \mu )\; =\; \Gamma \; (1\; -\; s)\; (-\; \mu )\; s\; -\; 1\; +\; \Gamma \; (1\; -\; s)\; \sum \; h\; =\; 1\; \infty \; [(-\; 2\; h\; \pi \; i\; -\; \mu )\; s\; -\; 1\; +\; (2\; h\; \pi \; i\; -\; \mu )\; s\; -\; 1].\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; \backslash \; Gamma\; (1-s)\; (-\; \backslash \; mu)\; ^\; \{s-1\}\; +\; \backslash \; Gamma\; (1-s)\; \backslash \; sum\; \_\; \{h\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; [(-\; 2h\; \backslash \; pi\; i-\; \backslash \; mu)\; ^\; \{s-1\}\; +\; (2h\; \backslash \; pi\; i-\; \backslash \; mu)\; ^\; \{s-1\}\; \backslash \; right].\}$

Когда биномиальные степени в сумме разложены до µ = 0 и порядок суммирования меняется на противоположный, сумма по h может быть выражена в замкнутой форме:

$Li\; s\; \; (e\; \mu )\; =\; \Gamma \; (1\; -\; s)\; (-\; \mu )\; s\; -\; 1\; +\; \sum \; К\; знак\; равно\; 0\; \infty \; \zeta \; (s\; -\; К)\; К!\; \mu \; k.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; \backslash \; Gamma\; (1-s)\; (-\; \backslash \; mu)\; ^\; \{s-1\}\; +\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\; \backslash \; infty\}\; \{\backslash \; zeta\; (sk)\; \backslash \; over\; k!\}\; \backslash \; mu\; ^\; \{k\}.\}$

Этот результат верен для | µ | <2π и благодаря аналитическому продолжению, обеспечемому дзета-функции, для всех s ≠ 1, 2, 3,.... Если порядок является положительным целым числом, s = n, оба члена с k = n - 1 и гамма-функция большие бесконечными, хотя их сумма - нет. Получается (Wood 1992, § 9; Gradshteyn Ryzhik 1980, § 9.554 harvnb error: no target: CITEREFGradshteynRyzhik1980 (help )):

$lim\; s\; \to \; к\; +\; 1\; [\zeta \; (s\; -\; k)\; к!\; \mu \; k\; +\; \Gamma \; (1\; -\; s)\; (-\; \mu )\; s\; -\; 1]\; =\; \mu \; k\; k!\; [\sum \; час\; =\; 1\; К\; 1\; час\; -\; пер\; \; (-\; \mu )],\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{s\; \backslash \; to\; k\; +\; 1\}\; \backslash \; left\; [\{\backslash \; zeta\; (sk)\; \backslash \; over\; k!\}\; \backslash \; Mu\; ^\; \{k\; \}\; +\; \backslash \; Gamma\; (1-s)\; (-\; \backslash \; mu)\; ^\; \{s-1\}\; \backslash \; right]\; =\; \{\backslash \; mu\; ^\; \{k\}\; \backslash \; over\; k!\}\; \backslash \; Left\; [\backslash \; sum\; \_\; \{h\; =\; 1\}\; ^\; \{k\; \}\; \{1\; \backslash \; over\; h\}\; -\; \backslash \; ln\; (-\; \backslash \; mu)\; \backslash \; right],\}$

где сумма по h обращается в нуль, если k = 0. Итак, для положительных целочисленных порядков и для | μ | < 2π we have the series:

$Li\; n\; \; (e\; \mu )\; =\; \mu \; n\; -\; 1\; (n\; -\; 1)!\; [H\; n\; -\; 1\; -\; ln\; \; (-\; \mu )]\; +\; \sum \; k\; знак\; равно\; 0,\; k\; \ne \; n\; -\; 1\; \infty \; \zeta \; (n\; -\; k)\; k!\; \mu \; К,\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{n\}\; (e\; ^\; \{\backslash \; mu\})\; =\; \{\backslash \; mu\; ^\; \{n-1\}\; \backslash \; over\; (n-1)!\}\; \backslash \; left\; [H\_\; \{n-1\; \}\; -\; \backslash \; ln\; (-\; \backslash \; mu)\; \backslash \; right]\; +\; \backslash \; sum\; \_\; \{k\; =\; 0,\; k\; \backslash \; neq\; n-1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; zeta\; (nk)\; \backslash \; over\; k!\}\; \backslash \; mu\; ^\; \{k\},\}$

где H n обозначает номер n-й гармоники :

$H\; n\; =\; \sum \; h\; =\; 1\; n\; 1\; h,\; H\; 0\; =\; 0.\; \{\backslash \; displaystyle\; H\_\; \{n\}\; =\; \backslash \; sum\; \_\; \{h\; =\; 1\}\; ^\; \{n\}\; \{1\; \backslash \; over\; h\},\; \backslash \; qquad\; H\_\; \{0\}\; =\; 0.\}$

Теперь члены задачи содержат −ln (−μ), которое при умножении на μ будет стремятся к нулю при μ → 0, за исключением n = 1. Это отражает тот факт, что Li s (z) демонстрирует истинную логарифмическую особенность при s = 1 и z = 1, поскольку :

$lim\; \mu \; \to \; 0\; \Gamma \; (1\; -\; s)\; (-\; \mu )\; s\; -\; 1\; =\; 0\; (Re\; \; (s)>1).\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; 0\}\; \backslash \; Gamma\; (1-s)\; (-\; \backslash \; mu)\; ^\; \{s-1\}\; =\; 0\; \backslash \; qquad\; (\backslash \; operatorname\; \{Re\}\; (s)>1).\}$

Для s, близкого, но не равного положительному целому числу, можно ожидать, что расходящиеся члены в разложении около µ = 0 вызовут вычислительные трудности (Wood 1992, § 9). Соответствующее разложение Эрдейи (Erdélyi et al. 1981, § 1.11-15) в степенях ln (z) неверно, если предположить, что главные ветви полилогарифма и логарифма используются одновременно, поскольку ln (⁄ z) не всегда равно −ln (z).

Для неположительных целочисленных значений s дзета-функция ζ (s - k) в разложении около µ = 0 сводится к Числа Бернулли : ζ (−n - k) = −B 1 + n + k / (1 + n + k). Численное вычисление Li −n (z) этой серии не страдает от эффекта отмены cts, которые конечные рациональные выражения, указанные в разделе конкретные значения выше, демонстрируют для больших n.

3.Используя тождество

$1\; =\; 1\; \Gamma \; (s)\; \int \; 0\; \infty \; e\; -\; tts\; -\; 1\; dt\; (Re\; \; (s)>0),\; \{\backslash \; displaystyle\; 1\; =\; \{1\; \backslash \; over\; \backslash \; Gamma\; (s)\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; t\}\; t\; ^\; \{s-1\}\; dt\; \backslash \; qquad\; (\backslash \; operatorname\; \{Re\}\; (s)>0),\}$

Bose– Интегральное представление Эйнштейна полилогарифма (см. Выше) может быть представлено в виде:

$Li\; s\; \; (z)\; =\; 1\; 2\; z\; +\; z\; 2\; \Gamma \; (s)\; \int \; 0\; \infty \; e\; -\; tts\; -\; 1\; coth\; \; T\; -\; пер\; \; Z\; 2\; dt\; (Re\; \; (s)>0).\; \{\backslash \; Displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; z\; +\; \{z\; \backslash \; над\; 2\; \backslash \; Gamma\; (s)\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; e\; ^\; \{-\; t\}\; t\; ^\; \{s-1\}\; \backslash \; coth\; \{t-\; \backslash \; ln\; z\; \backslash \; over\; 2\}\; dt\; \backslash \; qquad\; (\backslash \; operatorname\; \{Re\}\; (s)>0).\}$

Замена гиперболического котангенса на двусторонний ряд,

$coth\; \; t\; -\; ln\; \; z\; 2\; =\; 2\; \sum \; К\; знак\; равно\; -\; \infty \; \infty \; 1\; 2\; К\; \pi \; я\; +\; T\; -\; пер\; \; Z,\; \{\backslash \; Displaystyle\; \backslash \; coth\; \{t-\; \backslash \; ln\; z\; \backslash \; над\; 2\}\; =\; 2\; \backslash \; сумма\; \_\; \{к\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\; \}\; \{1\; \backslash \; over\; 2k\; \backslash \; pi\; i\; +\; t-\; \backslash \; ln\; z\},\}$

затем меняют порядок интеграла и суммы и, наконец, идентифицируют слагаемые с интегральным представлением верхней неполной гамма-функции, получаем:

$Li\; s\; \; (z)\; =\; 1\; 2\; z\; +\; \sum \; k\; =\; -\; \infty \; \infty \; \Gamma \; (1\; -\; s,\; 2\; k\; \pi \; i\; -\; ln\; \; z)\; (2\; k\; \pi \; i\; -\; ln\; \; z)\; 1\; -\; с.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; z\; +\; \backslash \; sum\; \_\; \{k\; =\; -\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; Gamma\; (1-s,\; 2k\; \backslash \; pi\; i-\; \backslash \; ln\; z)\; \backslash \; over\; (2k\; \backslash \; pi\; i-\; \backslash \; ln\; z)\; ^\; \{1-s\}\}.\}$

Как для двустороннего ряда этого результата, так и для гиперболического котангенса симметричный частичный суммы от -k max до k max безусловно сходятся при k max → ∞. При условии, что суммирование выполняется симметрично, этот ряд для Li s (z), таким образом, выполняется для всех комплексных s, а также для всех комплексных z.

4.Вводя явное выражение для чисел Стирлинга второго рода в конечную сумму для полилогарифма неположительного целочисленного порядка (см. Выше), можно написать:

$Li\; -\; n\; \; (z)\; =\; \sum \; k\; =\; 0\; n\; (-\; z\; 1\; -\; z)\; k\; +\; 1\; \sum \; j\; =\; 0\; k\; (-\; 1)\; j\; +\; 1\; (kj)\; (j\; +\; 1)\; n\; (n\; =\; 0,\; 1,\; 2,\dots ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{-\; n\}\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{n\}\; \backslash \; left\; (\{-\; z\; \backslash \; over\; 1-z\}\; \backslash \; right)\; ^\; \{k\; +\; 1\}\; \backslash \; sum\; \_\; \{j\; =\; 0\}\; ^\; \{k\}\; (-\; 1)\; ^\; \{j\; +\; 1\}\; \{k\; \backslash \; choose\; j\}\; (j\; +\; 1)\; ^\; \{n\}\; \backslash \; qquad\; (n\; =\; 0,1,2,\; \backslash \; ldots).\}$

Бесконечный ряд, полученный простым продолжением внешнего суммирования до ∞ (Guillera Sondow 2008, теорема 2.1):

$Li\; s\; \; (z)\; =\; \sum \; k\; =\; 0\; \infty \; (\; -\; Z\; 1\; -\; Z)\; К\; +\; 1\; \sum \; J\; знак\; равно\; 0\; К\; (-\; 1)\; J\; +\; 1\; (KJ)\; (J\; +\; 1)\; -\; s,\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \backslash \; сумма\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (\{-\; z\; \backslash \; over\; 1-z\}\; \backslash \; right)\; ^\; \{k\; +\; 1\}\; ~\; \backslash \; sum\; \_\; \{j\; =\; 0\}\; ^\; \{k\}\; (-\; 1)\; ^\; \{j\; +\; 1\}\; \{k\; \backslash \; choose\; j\}\; (j\; +\; 1)\; ^\; \{-\; s\},\}$

оказывается сходящимся к полилогарифму для всех комплексных s и комплексных z с Re (z) < ⁄2, что можно проверить для | ⁄ ​​(1 − z) | < ⁄2, изменив порядок суммирования и используя:

$\sum \; k\; =\; j\; \infty \; (kj)\; (-\; z\; 1\; -\; z)\; k\; +\; 1\; =\; [\; (-\; z\; 1\; -\; z)\; -\; 1\; -\; 1]\; -\; j\; -\; 1\; =\; (-\; z)\; j\; +\; 1.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{k\; =\; j\}\; ^\; \{\backslash \; infty\}\; \{k\; \backslash \; select\; j\}\; \backslash \; left\; (\{-\; z\; \backslash \; over\; 1-z\}\; \backslash \; right)\; ^\; \{k\; +\; 1\}\; =\; \backslash \; left\; [\backslash \; left\; (\; \{-z\; \backslash \; over\; 1-z\}\; \backslash \; right)\; ^\; \{-\; 1\}\; -1\; \backslash \; right]\; ^\; \{-\; j-1\}\; =\; (-\; z)\; ^\; \{j\; +\; 1\}.\}$

Внутренние коэффициенты этих серии могут быть выражается формулами , относящимися к количеству Стирлинга,, включающими обобщенные номера гармоник. Например, см. преобразования производящих функций, чтобы найти доказательства (ссылки на доказательства) следующих тождеств:

$Li\; 2\; \; (z)\; =\; \sum \; j\; \ge \; 1\; (-\; 1)\; j\; -\; 1\; 2\; (H\; j\; 2\; +\; H\; j\; (2))\; zj\; (1\; -\; z)\; j\; +\; 1\; Li\; 3\; \; (z)\; =\; \sum \; j\; \ge \; 1\; (-\; 1)\; j\; -\; 1\; 6\; (H\; j\; 3\; +\; 3\; H\; j\; H\; j\; (2)\; +\; 2\; H\; j\; (\; 3))\; zj\; (1\; -\; z)\; j\; +\; 1.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; =\; \backslash \; sum\; \_\; \{j\; \backslash \; geq\; 1\}\; \{\backslash \; frac\; \{(\; -1)\; ^\; \{j-1\}\}\; \{2\}\}\; \backslash \; left\; (H\_\; \{j\}\; ^\; \{2\}\; +\; H\_\; \{j\}\; ^\; \{(2)\}\; \backslash \; right)\; \{\backslash \; frac\; \{z\; ^\; \{j\}\}\; \{\; (1-z)\; ^\; \{j\; +\; 1\}\}\}\; \backslash \backslash \backslash \; operatorname\; \{Li\}\; \_\; \{3\}\; (z)\; =\; \backslash \; sum\; \_\; \{j\; \backslash \; geq\; 1\}\; \{\backslash \; frac\; \{(-1)\; ^\; \{j-\; 1\}\}\; \{6\}\}\; \backslash \; left\; (H\_\; \{j\}\; ^\; \{3\}\; +\; 3H\_\; \{j\}\; H\_\; \{j\}\; ^\; \{(2)\}\; +\; 2H\_\; \{j\}\; ^\; \{(3)\}\; \backslash \; right)\; \{\backslash \; frac\; \{z\; ^\; \{j\}\}\; \{(1-z)\; ^\; \{j\; +\; 1\}\}\}.\; \backslash \; end\; \{align\}\}\}$

Для других аргументов с Re (z) < ⁄2результат следует за аналитическим продолжением. Эта процедура эквивалентна применения преобразования Эйлера к ряду по z, определяющему полилогарифм.

Для | z | ≫ 1, полилогарифм можно разложить в асимптотический ряд через ln (−z):

$Li\; s\; \; (z)\; =\; \pm \; i\; \pi \; \Gamma \; (s)\; [ln\; \; (-\; z)\; \pm \; я\; \pi ]\; s\; -\; 1\; -\; \sum \; К\; знак\; равно\; 0\; \infty \; (-\; 1)\; К\; (2\; \pi )\; 2\; К\; Б\; 2\; К\; (2\; К)!\; [пер\; \; (-\; Z)\; \pm \; я\; \pi ]\; s\; -\; 2\; К\; \Gamma \; (s\; +\; 1-2\; к),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \{\backslash \; pm\; я\; \backslash \; пи\; \backslash \; над\; \backslash \; Гамма\; (ы)\}\; [\backslash \; ln\; (-z)\; \backslash \; pm\; i\; \backslash \; pi]\; ^\; \{s-1\}\; -\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\}\; (-\; 1)\; ^\; \{k\}\; (2\; \backslash \; pi)\; ^\; \{2k\}\; \{B\_\; \{2k\}\; \backslash \; over\; (2k)!\}\; \{[\backslash \; Ln\; (-z)\; \backslash \; pm\; i\; \backslash \; pi]\; ^\; \{s-2k\}\; \backslash \; over\; \backslash \; Gamma\; (s\; +\; 1-2k)\},\; \}$

$Li\; s\; \; (z)\; =\; \sum \; k\; =\; 0\; \infty \; (-\; 1)\; k\; (1-2\; 1\; -\; 2\; k)\; (2\; \pi )\; 2\; k\; B\; 2\; k\; (2\; k)!\; [пер\; \; (-\; Z)]\; s\; -\; 2\; К\; \Gamma \; (s\; +\; 1-2\; к),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; \backslash \; sum\; \_\; \{k\; =\; 0\}\; ^\; \{\backslash \; infty\; \}\; (-\; 1)\; ^\; \{k\}\; (1-2\; ^\; \{1-2k\})\; (2\; \backslash \; pi)\; ^\; \{2k\}\; \{B\_\; \{2k\}\; \backslash \; over\; (2k)!\}\; \{[\backslash \; Ln\; (-z)]\; ^\; \{s-2k\}\; \backslash \; over\; \backslash \; Gamma\; (s\; +\; 1-2k)\},\}$

где B 2k - числа Бернулли. Обе версии верны для всех s и для любого arg (z). Как правило, суммирование должно быть прекращено, когда начинается рост по величине. Для отрицательного целого s разложения полностью исчезают; для целого неотрицательного s они обрываются после конечного числа членов. Вуд (1992, § 11) вызов метод получения этих рядов из интегрального представления Бозе - Эйнштейна (его уравнение 11.2 для Li s (e) требует −2π < Im(µ) ≤ 0).

Следующие ограничения вызывают результатом различных представлений полилогарифма (Wood 1992, § 22):

$lim\; |\; z\; |\; \to \; 0\; Li\; s\; \; (z)\; знак\; равно\; z\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{|\; z\; |\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; z\}$

$lim\; Re\; \; (\mu )\; \to \; \infty \; Li\; s\; \; (e\; \mu )\; =\; -\; \mu \; s\; \Gamma \; (s\; +\; 1)\; (s\; \ne \; -\; 1),\; -\; 2,\; -\; 3,\dots )\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; operatorname\; \{Re\}\; (\backslash \; mu)\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (e\; ^\; \{\backslash \; mu\})\; =\; -\; \{\; \backslash \; mu\; ^\; \{s\}\; \backslash \; over\; \backslash \; Gamma\; (s\; +\; 1)\}\; \backslash \; qquad\; (s\; \backslash \; neq\; -1,\; -2,\; -3,\; \backslash \; ldots)\}$

$lim\; Re\; \; (\mu )\; \to \; \infty \; Li\; -\; N\; \; (е\; \mu )\; знак\; равно\; -\; (-\; 1)\; ne\; -\; \mu \; (n\; =\; 1,\; 2,\; 3,\dots )\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; operatorname\; \{Re\}\; (\backslash \; mu)\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{Li\; \}\; \_\; \{-\; n\}\; (e\; ^\; \{\backslash \; mu\})\; =\; -\; (-\; 1)\; ^\; \{n\}\; e\; ^\; \{-\; \backslash \; mu\}\; \backslash \; qqu\; ad\; (N\; =\; 1,2,3,\; \backslash \; ldots)\}$

$lim\; Re\; \; (s)\; \to \; \infty \; Li\; s\; \; (z)\; знак\; равно\; z\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; operatorname\; \{Re\}\; (s)\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (z)\; =\; z\}$

$lim\; Re\; \; (s)\; \to \; -\; \infty \; Li\; s\; \; (-\; e\; \mu )\; =\; \Gamma \; (1\; -\; s)\; [(-\; \mu \; -\; \pi )\; s\; -\; 1\; +\; (-\; \mu \; +\; \pi )\; s\; -\; 1]\; (Im\; \; (\mu )\; =\; 0)\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; operatorname\; \{Re\}\; (s)\; \backslash \; к\; -\; \backslash \; infty\}\; \backslash \; operatorname\; \{Li\}\; \_\; \{s\}\; (-\; e\; ^\; \{\backslash \; mu\})\; =\; \backslash \; Gamma\; (1-s)\; \backslash \; left\; [(-\; \backslash \; mu\; -i\; \backslash \; pi)\; ^\; \{s-1\}\; +\; (-\; \backslash \; mu\; +\; i\; \backslash \; pi)\; ^\; \{s-1\}\; \backslash \; right]\; \backslash \; qquad\; (\backslash \; operatorname\; \{Im\}\; (\backslash \; mu)\; =\; 0)\}$

Первый предел Вуда для Re (µ) → ∞ был исправлен в соответствии с его уравнением 11.3. Предел для Re (s) → −∞ следует из общей связи полилогарифма с дзета-функцией Гурвица (см. Выше).

Дилогарифм - это полилогарифм порядка s = 2. Альтернативным интегральным выражением дилогарифма для произвольного комплексного аргумента z является (Abramowitz Stegun 1972, § 27.7):

$Li\; 2\; \; (z)\; =\; -\; \int \; 0\; z\; ln\; \; (1\; -\; t)\; tdt\; =\; -\; \int \; 0\; 1\; ln\; \; (1\; -\; zt)\; tdt.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; =\; -\; \backslash \; int\; \_\; \{0\}\; ^\; \{z\}\; \{\backslash \; ln\; (1-t)\; \backslash \; over\; t\}\; dt\; =\; -\; \backslash \; int\; \_\; \{0\}\; ^\; \{\; 1\}\; \{\backslash \; ln\; (1-zt)\; \backslash \; over\; t\}\; dt.\}$

Источник путаницы состоит в том, что некоторые системы компьютерной алгебры определяют дилогарифм как dilog (z) = Li 2 (1-z).

В случае действительного z ≥ 1 первое интегральное выражение для дилогарифма может быть записано как

$Li\; 2\; \; (z)\; =\; \pi \; 2\; 6\; -\; \int \; 1\; z\; ln\; \; (t\; -\; 1)\; tdt\; -\; я\; \pi \; ln\; \; z\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; =\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\}\; \{6\}\}\; -\; \backslash \; int\; \_\; \{1\}\; ^\; \{z\}\; \{\backslash \; ln\; (t-1)\; \backslash \; over\; t\}\; dt-i\; \backslash \; pi\; \backslash \; ln\; z\}$

, из которого, раскладывая ln (t − 1) и почленно интегрировав, получаем

$Li\; 2\; \; (z)\; =\; \pi \; 2\; 3\; -\; 1\; 2\; (ln\; \; z)\; 2\; -\; \sum \; k\; =\; 1\; \infty \; 1\; k\; 2\; zk\; -\; я\; \pi \; ln\; \; z\; (z\; \ge \; 1).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; =\; \{\backslash \; frac\; \{\backslash \; pi\; ^\; \{2\}\}\; \{3\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (\backslash \; ln\; z)\; ^\; \{2\; \}\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{1\; \backslash \; over\; k\; ^\; \{2\}\; z\; ^\; \{k\}\}\; -\; i\; \backslash \; pi\; \backslash \; ln\; z\; \backslash \; qquad\; (z\; \backslash \; geq\; 1).\}$

Тождество Абеля для дилогарифма дается выражением (Абель 1881)

$Li\; 2\; \; (x\; 1\; -\; y)\; +\; Li\; 2\; \; (y\; 1\; -\; x)\; -\; Li\; 2\; \; (xy\; (\; 1\; -\; Икс)\; (1\; -\; Y))\; знак\; равно\; Ли\; 2\; \; (Икс)\; +\; Li\; 2\; \; (Y)\; +\; пер\; \; (1\; -\; х)\; пер\; \; (1\; -\; у)\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{Li\}\; \_\; \{2\; \}\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{1-y\}\}\; \backslash \; right)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{y\}\; \{1-x\}\}\; \backslash \; right)\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{xy\}\; \{(1-x)\; (1-y)\}\}\; \backslash \; right)\; =\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (x)\; +\; \backslash \; operatorname\; \{Li\; \}\; \_\; \{2\}\; (y)\; +\; \backslash \; ln\; (1-x)\; \backslash \; ln\; (1-y)\}$

Сразу видно, что это выполняется либо для x = 0, либо для y = 0, и для общих аргументов легко проверить дифференцированием ∂ / ∂x ∂ / ∂y. F или y = 1 − x тождество сводится к формуле отражения Эйлера

$Li\; 2\; \; (x)\; +\; Li\; 2\; \; (1\; -\; x)\; =\; 1\; 6\; \pi \; 2\; -\; ln\; \; (x)\; пер\; \; (1\; -\; х),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (x\; \backslash \; right)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (1-x\; \backslash \; right)\; =\; \{\backslash \; frac\; \{1\}\; \{6\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; (x)\; \backslash \; ln\; (1-x),\}$

где Li 2 (1) = ζ (2) = ⁄ 6 π, и x может принимать любое комплексное значение.

В терминах новых переменных u = x / (1 − y), v = y / (1 − x) тождество Абеля читается как

$Li\; 2\; \; (u)\; +\; Li\; 2\; \; (v)\; -\; Li\; 2\; \; (uv)\; =\; Li\; 2\; \; (u\; -\; uv\; 1\; -\; uv)\; +\; Li\; 2\; \; (v\; -\; uv\; 1\; -\; uv)\; +\; ln\; \; (1\; -\; u\; 1\; -\; uv)\; ln\; \; (1\; -\; v\; 1\; -\; uv),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (u)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (v)\; -\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (uv)\; =\; \backslash \; operatorname\; \{Li\; \}\; \_\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{u-uv\}\; \{1-uv\}\}\; \backslash \; right)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (\{\backslash \; frac\; \{v-uv\}\; \{1-uv\; \}\}\; \backslash \; right)\; +\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1-u\}\; \{1-uv\}\}\; \backslash \; right)\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1-v\}\; \{1-uv\}\}\; \backslash \; right),\}$

, что соответствует пятиугольнику, указанному в (Rogers 1907).

Из тождества Абеля для x = y = 1 − z и квадратного отношения мы получаем тождество Ландена

$Li\; 2\; \; (1\; -\; z)\; +\; Li\; 2\; \; (\; 1\; -\; 1\; z)\; знак\; равно\; -\; 1\; 2\; (пер\; \; z)\; 2\; (z\; \notin ]\; -\; \infty ;\; 0]),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (1-z)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{1\}\; \{z\}\}\; \backslash \; right)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; (\backslash \; ln\; z)\; ^\; \{2\}\; \backslash \; qquad\; (z\; \backslash \; not\; \backslash \; in\; ~]\; -\; \backslash \; infty;\; 0]),\}$

и применяя формулу отражения к каждому дилогарифму, находим формулу обращения

$Li\; 2\; \; (z)\; +\; Li\; 2\; \; (1\; /\; z)\; =\; -\; 1\; 6\; \pi \; 2\; -\; 1\; 2\; [пер\; \; (-\; z)]\; 2\; (z\; \notin \; [0;\; 1\; [),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (1\; /\; z)\; =\; -\; \{\backslash \; tfrac\; \{1\}\; \{6\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; [\backslash \; ln\; (-z)]\; ^\; \{2\}\; \backslash \; qquad\; (z\; \backslash \; not\; \backslash \; in\; [0;\; 1\; [),\}$

и для вещественного z ≥ 1 также

$Li\; 2\; \; (z)\; +\; Li\; 2\; \; (1\; /\; z)\; =\; 1\; 3\; \pi \; 2\; -\; 1\; 2\; (ln\; \; z)\; 2\; -\; i\; \pi \; ln\; \; z.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (z)\; +\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (1\; /\; z)\; =\; \{\backslash \; tfrac\; \{1\}\; \{3\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (\backslash \; ln\; z)\; ^\; \{2\}\; -i\; \backslash \; pi\; \backslash \; ln\; z.\}$

В таблице ниже собраны известные вычисления дилогарифма в закрытой форме при специальных аргументах. Аргументы в первом столбце связаны отражением x ↔ 1 − x или инверсией x ↔ ⁄ x либо с x = 0, либо с x = −1; все аргументы в третьем столбце связаны между собой этими операциями.

Максимон (2003) обсуждает ссылки 17-19 веков. Формула отражения была уже опубликована Ланденом в 1760 году до ее появления в книге Эйлера 1768 года (Maximon 2003, § 10); эквивалент личности Абеля был уже опубликован в 1809 году, до того, как Абель написал свою рукопись в 1826 году (Zagier 1989, § 2). Обозначение bilogarithmische Function было введено Карлом Йоханом Даниэльссоном Хиллом (профессором из Лунда, Швеция) в 1828 году (Maximon 2003, § 10). Дон Загир (1989) заметил, что дилогарифм - единственная математическая функция, обладающая чувством юмора.

Специальные значения дилогарифма

$x\; \{\backslash \; displaystyle\; x\}$	$Li\; 2\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (x)\}$	$x\; \{\backslash \; displaystyle\; x\; \}$	$Li\; 2\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (x)\}$
$-\; 1\; \{\backslash \; displaystyle\; -1\}$	$-\; 1\; 12\; \pi \; 2\; \{\backslash \; displaystyle\; -\; \{\; \backslash \; tfrac\; \{1\}\; \{12\}\}\; \backslash \; pi\; ^\; \{2\}\}$	$-\; \varphi \; \{\backslash \; displaystyle\; -\; \backslash \; phi\}$	$-\; 1\; 10\; \pi \; 2\; -\; ln\; 2\; \; \varphi \; \{\backslash \; displaystyle\; -\; \{\backslash \; tfrac\; \{1\; \}\; \{10\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; ^\; \{2\}\; \backslash \; phi\}$
$0\; \{\backslash \; displaystyle\; 0\}$	$0\; \{\backslash \; displaystyle\; 0\}$	$-\; 1\; /\; \varphi \; \{\backslash \; displaystyle\; -\; 1\; /\; \backslash \; phi\}$	$-\; 1\; 15\; \pi \; 2\; +\; 1\; 2\; ln\; 2\; \; \varphi \; \{\backslash \; displaystyle\; -\; \{\backslash \; tfrac\; \{1\}\; \{15\}\}\; \backslash \; pi\; ^\; \{2\}\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\; \}\; \backslash \; ln\; ^\; \{2\}\; \backslash \; phi\}$
$1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\}$	$1\; 12\; \pi \; 2\; -\; 1\; 2\; ln\; 2\; \; 2\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\; 1\}\; \{12\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; ln\; ^\; \{2\}\; 2\}$	$1\; /\; \varphi \; 2\; \{\backslash \; displaystyle\; 1\; /\; \backslash \; phi\; ^\; \{2\}\}$	$1\; 15\; \pi \; 2\; -\; пер\; 2\; \; \varphi \; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{15\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; ^\; \{2\}\; \backslash \; phi\}$
$1\; \{\backslash \; displaystyle\; 1\}$	$1\; 6\; \pi \; 2\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{6\}\}\; \backslash \; pi\; ^\; \{2\}\}$	$1\; /\; \varphi \; \{\backslash \; displaystyle\; 1\; /\; \backslash \; phi\}$	$1\; 10\; \pi \; 2\; -\; ln\; 2\; \; \varphi \; \{\backslash \; di\; splaystyle\; \{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; ^\; \{2\}\; \backslash \; phi\}$
$2\; \{\backslash \; displaystyle\; 2\}$	$1\; 4\; \pi \; 2\; -\; \pi \; i\; ln\; \; 2\; \{\; \backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{4\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; pi\; i\; \backslash \; ln\; 2\}$	$\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$	$11\; 15\; \pi \; 2\; +\; 1\; 2\; ln\; 2\; \; (\; -\; 1\; /\; \varphi )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{11\}\; \{15\}\}\; \backslash \; pi\; ^\; \{2\}\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; ln\; ^\; \{2\}\; (-\; 1\; /\; \backslash \; phi)\}$
		$\varphi \; 2\; \{\backslash \; displaystyle\; \backslash \; phi\; ^\; \{2\}\}$	$-\; 11\; 15\; \pi \; 2\; -\; ln\; 2\; \; (-\; \varphi )\; \{\backslash \; displaystyle\; -\; \{\backslash \; tfrac\; \{11\}\; \{15\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; ^\; \{2\}\; (-\; \backslash \; phi)\}$

Здесь $\varphi \; =\; 1\; 2\; (5\; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; phi\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (\{\backslash \; sqrt\; \{\; 5\}\}\; +\; 1)\}$обозначает золотое сечение.

Леонард Левин обнаружил замечательное и широкое обобщение ряда классических соотношений полилогарифма для специальных ценности. Теперь они называются лестницами полилогарифма. Определите $\rho \; =\; 1\; 2\; (5-1)\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; (\{\backslash \; sqrt\; \{5\}\}\; -\; 1)\}$как обратное золотого сечения. Тогда два простых примера лестниц дилогарифма:

$Li\; 2\; \; (\rho \; 6)\; =\; 4\; Li\; 2\; \; (\rho \; 3)\; +\; 3\; Li\; 2\; \; (\rho \; 2)\; -\; 6\; Li\; 2\; \; (\rho )\; +\; 7\; 30\; \pi \; 2\; \{\; \backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\backslash \; rho\; ^\; \{6\})\; =\; 4\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\backslash \; rho\; ^\; \{3\})\; +\; 3\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\; \backslash \; rho\; ^\; \{2\})\; -\; 6\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\backslash \; rho)\; +\; \{\backslash \; tfrac\; \{7\}\; \{30\}\}\; \backslash \; pi\; ^\; \{2\}\}$

получено Кокстером (1935) и

$Li\; 2\; \; (\rho )\; =\; 1\; 10\; \pi \; 2\; -\; ln\; 2\; \; \rho \; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Li\}\; \_\; \{2\}\; (\backslash \; rho)\; =\; \{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; pi\; ^\; \{2\}\; -\; \backslash \; ln\; ^\; \{2\}\; \backslash \; rho\}$

задано Ланденом. Лестницы полилогарифма естественным образом и глубоко используются в K-теории и алгебраической геометрии. Лестницы полилогарифмов обеспечивают основу для быстрых вычислений различных математических констант с помощью алгоритма BBP (Bailey, Borwein Plouffe 1997).

Полилогарифм имеет две точки ветвления ; одна при z = 1, а другая при z = 0. Вторая точка ветвления при z = 0 не видна на основном листе полилогарифма; он становится видимым только тогда, когда функция аналитически продолжается на другие ее листы. Группа монодромии для полилогарифма состоит из гомотопических классов петель, которые наматываются вокруг двух точек ветвления. Обозначая эти два значения m 0 и m 1, группа монодромии имеет представление группы

$m\; 0,\; m\; 1\; |\; вес\; =\; м\; 0\; м\; 1\; м\; 0\; -\; 1\; м\; 1\; -\; 1,\; вес\; м\; 1\; =\; м\; 1\; w⟩.\; \{\backslash \; displaystyle\; \backslash \; langle\; m\_\; \{0\},\; m\_\; \{1\}\; \backslash \; vert\; w\; =\; m\_\; \{0\}\; m\_\; \{1\}\; m\_\; \{0\}\; ^\; \{-\; 1\}\; m\_\; \{1\}\; ^\; \{-\; 1\},\; wm\_\; \{1\}\; =\; m\_\; \{1\}\; w\; \backslash \; rangle.\}$

Для особого случая дилогарифма также имеется wm 0 = m 0 w, и группа монодромии становится Группа Гейзенберга (идентифицирующая m 0, m 1 и w с помощью x, y, z) (Vepstas 2008).

• Abel, N.H. (1881) [1826]. "Обратите внимание на функцию $\psi \; x\; =\; x\; +\; x\; 2\; 2\; 2\; +\; x\; 3\; 3\; 2\; +\; \cdots \; +\; xnn\; 2\; +\; \cdots \; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; psi\; x\; =\; x\; +\; \{\backslash \; frac\; \{x\; ^\; \{2\; \}\}\; \{2\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{x\; ^\; \{3\}\}\; \{3\; ^\; \{2\}\}\}\; +\; \backslash \; cdots\; +\; \{\backslash \; frac\; \{x\; ^\; \{n\}\}\; \{n\; ^\; \{2\}\}\; \}\; +\; \backslash \; cdots\}$" (PDF). In Sylow, L.; Lie, S. (ред.). Œuvres complete de Niels Henrik Abel - Nouvelle édition, Tome II (на французском языке). Christiania [Oslo]: Grøndahl Søn. Pp. 189–193. CS1 maint: ref = harv (ссылка ) (эта рукопись 1826 г. была опубликована только посмертно.)
• Abramowitz, M.; Stegun, IA (1972) Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Dover Publications. ISBN 978-0-486-61272-0. CS1 maint: ref = harv (ссылка )
• Апостол, TM (2010), «Полилогарифм», в Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Справочник по математическим функциям NIST, Cambridge University Press, ISBN 978-0-521- 19225-5, MR 2723248 К S1 maint: ref = harv (ссылка )
• Bailey, D.H. ; Borwein, P.B. ; Plouffe, S. (апрель 1997 г.). «О быстром вычислении различных полилогарифмических констант» (PDF). Математика вычислений. 66 (218): 903–913. Bibcode : 1997MaCom..66..903B. doi : 10.1090 / S0025-5718-97-00856-9. CS1 maint: ref = harv (ссылка )
• Bailey, DH; Broadhurst, DJ (20 июня 1999 г.). «Лестница полилогарифма семнадцатого порядка». arXiv : math.CA/9906134. CS1 maint: ref = harv (link )
• Берндт, Британская Колумбия (1994). Записные книжки Рамануджана, Часть IV. Нью-Йорк: Springer-Verlag. Стр. 323–326. ISBN 978-0-387-94109-7. CS1 maint: ref = harv (link )
• Boersma, J. ; Dempsey, JP (1992). «Об оценке хи-функции Лежандра». Математика вычислений. 59 (199): 157–163. doi : 10.2307 / 2152987. JSTOR 2152987. CS1 maint: ref = harv (link )
• Borwein, D. ; Borwein, JM ; Girgensohn, R. (1995). " Явная оценка сумм Эйлера » (PDF). Труды Эдинбургского математического общества. Серия 2. 38 (2): 277–294. doi : 10.1017 /S0013091500019088.CS1 maint: ref = harv (lin k )
• Borwein, J.M.; Bradley, D.M.; Broadhurst, D.J.; Лисонек, П. (2001). «Особые значения кратных полилогарифмов». Труды Американского математического общества. 353 (3): 907–941. arXiv : math / 9910045. doi : 10.1090 / S0002-9947-00-02616-7. CS1 maint: ref = harv (ссылка )
• Бродхерст, DJ (21 апреля, 1996). «О перечислении неприводимых k-кратных сумм Эйлера и их роли в теории узлов и теории поля». arXiv : hep-th / 9604128. CS1 maint : ref = harv (link )
• Clunie, J. (1954). «О функциях Бозе-Эйнштейна». Proceedings of the Physical Society. Series A. 67 (7): 632– 636. Bibcode : 1954PPSA... 67..632C. doi : 10.1088 / 0370-1298 / 67/7/308. CS1 maint: ref = harv (ссылка )
• Cohen, H.; Lewin, L.; Zagier, D. (1992). «Полилогарифмовая лестница шестнадцатого порядка» (PS). Экспериментальная математика. 1 (1): 25–34. CS1 maint: ref = harv (link )
• Coxeter, HSM (1935) ». Функции Шлефли и Лобачефски ". Quarterly Journal of Mathematics (Oxford). 6 (1): 13–29. Bibcode : 1935QJMat... 6... 13C. doi : 10.1093 / qmath / os-6.1.13. JFM 61.0395.02. CS1 maint: ref = harv (ссылка )
• Cvijovic, D.; Клиновский, Дж. (1997). «Разложения в непрерывную дробь для дзета-функции Римана и полилогарифмы» (PDF). Труды Американского математического общества. 125 (9): 2543–2550. doi : 10.1090 / S0002-9939-97-04102-6. CS1 maint: ref = harv (ссылка )
• Cvijovic, D. (2007). «Новые интегральные представления функции полилогарифма». Труды Королевского общества A. 463 (2080): 897–905. arXiv : 0911.4452. Bibcode : 2007RSPSA.463..897C. doi : 10.1098 / rspa.2006.1794. CS1 maint: ref = harv (link )
• Erdélyi, A. ; Magnus, W.; Oberhettinger, F.; Tricomi, FG (1981). Higher Transcendental Functions, Vol. 1 (PDF). Малабар, Флорида: RE Krieger Publishing. ISBN 978-0-89874-206-0.(это перепечатка оригинала МакГроу – Хилла 1953 года)
• Форнберг, Б.; Кёльбиг, К.С. (1975). «Комплексные нули функции Жонкьера или полилогарифма». Математика вычислений. 29 (130): 582–599. doi : 10.2307 / 2005579. JSTOR 2005579. CS1 maint: ref = harv (ссылка )
• Научная библиотека GNU (2010). «Справочное руководство». Проверено 13 июня 2010 г.
• Градштейн, Израиль Соломонович ; Рыжик Иосиф Моисеевич ; Геронимус Юрий Вениаминович ; Цейтлин Михаил Юльевич ; Джеффри, Алан (2015) [октябрь 2014]. «9.553.». В Цвиллингере, Даниэль; Молл, Виктор Гюго (ред.). Таблица интегралов, серий и продуктов. Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. стр. 1050. ISBN 978-0-12-384933-5. LCCN 2014010276. CS1 maint: ref = harv (link )
• Guillera, J.; Sondow, J. (2008). «Двойные интегралы и бесконечность произведения для некоторых классических констант с помощью аналитического продолжения трансцендента Лерха ». The Ramanujan Journal. 16 (3): 247–270. arXiv : math.NT / 0506319. doi : 10.1007 / s11139-007-9102-0. CS1 maint: ref = harv (link )
• Hain, RM (25 марта, 1992). «Классические полилогарифмы». arXiv : alg-geom / 9202022. CS1 maint: ref = harv (link )
• Jahnke, E.; Эмде, Ф. (1945). Таблицы функций с формулами и кривыми (4-е изд.). Нью-Йорк: Dover Publications. CS1 maint: ref = harv (link )
• Jonquière, A. (1889)). "Примечание по серии $\sum \; n\; =\; 1\; \infty \; xnns\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{x\; ^\; \{n\}\}\; \{n\; ^\; \{s\}\}\}\}$" (PDF). Bulletin de la Société Mathématique de France (на французском языке). 17 : 142–152. doi : 10.24033 / bsmf.392. JFM 21.0246.02. CS1 maint: ref = harv (ссылка )
• Kölbig, K.S.; Mignaco, J.A.; Ремидди, Э. (1970). «Об обобщенных полилогарифмах Нильсена и их численном исчислении». НЕМНОГО. 10 : 38–74. doi : 10.1007 / BF01940890. CS1 maint: ref = harv (ссылка )
• Кириллов, А.Н. (1995). «Дилогарифмические тождества». Прогресс теоретической науки Приложение по физике. 118 : 61–142. arXiv : hep-th / 9408113. Bibcode : 1995PThPS.118...61K. doi : 10.1143 / PTPS.118.61. CS1 maint: ref = harv (ссылка )
• Левин, Л. (1958). Дилогарифмы и связанные функции. Лондон: Macdonald. MR 0105524. CS1 maint: ref = harv (ссылка )
• Левин, Л. (1981). Полилогарифмы и связанные функции. Новое Йорк: Северная Голландия. ISBN 978-0-444-00550-2. CS1 maint: ref = harv (link )
• Lewin, L., ed. (1991). Структурные свойства полилогарифмов. Математические обзоры и монографии. 37 . Providence, RI: Amer. Math. Soc. ISBN 978-0-8218 -1634-9. CS1 maint: ref = harv (ссылка )
• Маркман, Б. (1965). «Дзета-функция Римана». BIT. 5 : 138–141. CS1 maint: ref = h arv (ссылка )
• Maximon, L.C. (2003). «Функция дилогарифма для сложного аргумента». Труды Королевского общества A. 459 (2039): 2807–2819. Bibcode : 2003RSPSA.459.2807M. doi : 10.1098 / rspa.2003.1156. CS1 maint: ref = harv (ссылка )
• McDougall, J.; Stoner, EC (1938). «Вычисление функций Ферми-Дирака». Философские труды Королевского общества A. 237 (773): 67–104. Bibcode : 1938RSPTA.237... 67M. doi : 10.1098 / rsta.1938.0004. JFM 64.1500.04. CS1 maint: ref = harv (ссылка )
• Nielsen, N. (1909). «Der Eulersche Dilogarithmus und seine Verallgemeinerungen. Eine Monographie». Nova Acta Leopoldina (на немецком языке). Галле - Лейпциг, Германия: Kaiserlich-Leopoldinisch-Carolinische Deutsche Akademie der Naturforscher. XC (3): 121–212. JFM 40.0478.01. CS1 maint: ref = harv (ссылка )
• Прудников, А.П.; Маричев, О.И.; Брычков, Ю.А. (1990). Интегралы и ряды, Том 3: Другие специальные функции. Ньюарк, Нью-Джерси: Гордон и Брич. ISBN 978-2-88124-682-1. CS1 maint: ref = harv (ссылка ) (см. П. 1.2, «Обобщенная дзета-функция, многочлены Бернулли, многочлены Эйлера и полилогарифмы», стр. 23.)
• Робинсон, Дж. Э. (1951). «Замечание об интегральных функциях Бозе-Эйнштейна». Физический обзор. Серия 2. 83 (3): 678–679. Bibcode : 1951PhRv... 83..678R. doi : 10.1103 / PhysRev.83.678. CS1 maint: ref = harv (link )
• Rogers, LJ (1907). «Функция включения теоремы о суммах, связанные с рядом $\sum \; n\; =\; 1\; \infty \; xnn\; 2\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \backslash \; sum\; \_\; \{n\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{x\; ^\; \{n\}\}\; \{n\; ^\; \{2\}\; \}\}\}$". Протоколы Лондонского математического общества (2). 4 (1): 169–189. doi : 10.1112 / plms / s2-4.1.169. JFM 37.0428.03. CS1 maint: ref = harv (link )
• Schrödinger, E. (1952). Статистическая термодинамика (2-е изд.). Кембридж, Великобритания: Cambridge University Press. CS1 maint: ref = harv (ссылка )
• Truesdell, C. (1945). «О функции, которая встречается в Теория структуры полимеров ». Annals of Mathematics. Second Series. 46 (1): 144–157. doi : 10.2307 / 1969153. JSTOR 1969153. CS1 maint: ref = harv (ссылка )
• Вепстас, Л. (2008). «Эффективный алгоритм для ускорения сходимости колебательных рядов, полезный для вычисление полилогарифма и дзета-функций Гурвица ".Численные алгоритмы. 47 (3): 211–252. arXiv : math.CA/0702243. Bibcode : 2008NuAlg..47..211V. doi : 10.1007 / s11075-007-9153-8. CS1 maint: ref = harv (ссылка )
• Whittaker, ET ; Watson, GN (1927). A Course of Modern Analysis (4 ed.). Кембридж, Великобритания: Cambridge University Press. CS1 maint: ref = harv (ссылка ) (это издание переиздавалось много раз, в мягкой обложке 1996 года есть ISBN 0-521-09189-6.)
• Wirtinger, W. (1905). "Über eine besondere Dirichletsche Reihe". Journal für die Reine und Angewandte Mathematik (на немецком языке). 1905 (129): 214–219. doi : 10.1515 / crll.1905.129.214. JFM 37.0434.01. CS1 maint: ref = harv (ссылка )
• Вуд, округ Колумбия (июнь 1992 г.). «Вычисление полилогарифмов. Технический отчет 15-92 *» (PS). Кентербери, Великобритания: Компьютерная лаборатория Кентского университета. Дата обращения 1 ноября 2005 г. CS1 maint: ref = harv ( ссылка )
• Zagier, D. (1989). «Функция дилогарифма в геометрии и теории чисел». Теория чисел и связанные темы: доклады, представленные на Коллоквиуме Рамануджана, Бомбей, 1988 г. Исследования по математике. 12 . Бомбей: Институт фундаментальных исследований Тата и издательство Оксфордского университета. С. 231–249. ISBN 0-19-562367-3. CS1 maint: ref = harv (link ) (также обозначается как «Замечательный дилогарифм "в Journal of Mathematical and Physical Sciences 22 (1988), pp. 131–145, и в главе I (Zagier 2007).)
• Zagier, D. ( 2007). «Функция дилогарифма» (PDF). В Cartier, P.E.; и другие. (ред.). Границы теории чисел, физики и геометрии II - О конформных теориях поля, дискретных группах и перенормировке. Берлин: Springer-Verlag. С. 3–65. ISBN 978-3-540-30307-7. CS1 maint: ref = harv (ссылка )

• Weisstein, Eric W. «Полилогарифм». MathWorld.
• Вайсштейн, Эрик У. «Дилогарифм». MathWorld.
• Алгоритмы в аналитической теории чисел обеспечивает реализацию с произвольной точностью, на основе GMP, GPL -лицензионная реализация.