Гептадекагон

Многоугольник с 17 краями

Правильный семиугольник
Правильный семиугольник
Тип	Правильный многоугольник
Края и вершины	17
символ Шлефли	{17}
диаграмма Кокстера
группа симметрии	двугранный (D17), порядок 2 × 17
внутренний угол (градусы )	≈158,82 °
Двойной многоугольник	Собственный
Свойства	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрии гептадекагон или 17-угольник представляет собой семнадцатигранный многоугольник.

• 1 Правильный гептадекагон
  • 1.1 Конструкция
• 2 Симметрия
• 3 Связанные многоугольники
  • 3.1 Гептадекаграммы
  • 3.2 Многоугольники Петри
• 4 Ссылки
• 5 Дополнительная литература
• 6 Внешние ссылки

A правильный семиугольник представлен символом Шлефли {17}.

Конструкция

Так как 17 - это простое число Ферма, правильный семиугольник - это строящийся многоугольник (то есть тот, который может быть построен с использованием циркуля и немаркированной линейки ): это было показано Карлом Фридрихом Гауссом в 1796 году в возрасте 19 лет. Это доказательство представляет первый прогресс в строительстве регулярных полигонов за более чем 2000 лет. Доказательство Гаусса основывается, во-первых, на том факте, что конструктивность эквивалентна выразимости тригонометрических функций общего угла в терминах арифметических операций и извлечения квадратного корня, и во-вторых, о его доказательстве того, что это может быть сделано, если нечетные простые множители $N\; \{\backslash \; displaystyle\; N\}$, количества сторон правильного многоугольника, являются различными простыми числами Ферма, которые имеют вид $F\; n\; =\; 2\; 2\; n\; +\; 1\; \{\backslash \; displaystyle\; F\_\; \{n\}\; =\; 2\; ^\; \{2\; ^\; \{n\}\}\; +\; 1\}$для некоторого неотрицательного целого числа $n\; \{\backslash \; displaystyle\; n\}$. Таким образом, построение правильного семиугольника включает в себя нахождение косинуса $2\; \pi \; /\; 17\; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; /\; 17\}$в терминах квадратных корней, что включает уравнение степени 17 - простое число Ферма. Книга Гаусса Disquisitiones Arithmeticae дает это как (в современных обозначениях):

$16\; cos\; \; 2\; \pi \; 17\; =\; -\; 1\; +\; 17\; +\; 34\; -\; 2\; 17\; +\; 2\; 17\; +\; 3\; 17\; -\; 34\; -\; 2\; 17\; -\; 2\; 34\; +\; 2\; 17\; =\; -\; 1\; +\; 17\; +\; 34\; -\; 2\; 17\; +\; 2\; 17\; +\; 3\; 17\; -\; 170\; +\; 38\; 17.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; 16\; \backslash ,\; \backslash \; cos\; \{\backslash \; frac\; \{2\; \backslash \; pi\}\; \{17\}\}\; =\; -\; 1\; +\; \{\backslash \; sqrt\; \{17\}\}\; +\; \{\backslash \; sqrt\; \{34-2\; \{\backslash \; sqrt\; \{\; 17\}\}\}\}\; +\; \backslash \backslash \; 2\; \{\backslash \; sqrt\; \{17\; +\; 3\; \{\backslash \; sqrt\; \{17\}\}\; -\; \{\backslash \; sqrt\; \{34-2\; \{\backslash \; sqrt\; \{17\}\}\}\}\; -\; 2\; \{\backslash \; sqrt\; \{34\; +\; 2\; \{\; \backslash \; sqrt\; \{17\}\}\}\}\}\}\; \backslash \backslash \; =\; -\; 1\; +\; \{\backslash \; sqrt\; \{17\}\}\; +\; \{\backslash \; sqrt\; \{34-2\; \{\backslash \; sqrt\; \{17\}\}\}\}\; +\; \backslash \backslash \; 2\; \{\backslash \; sqrt\; \{17\; +3\; \{\backslash \; sqrt\; \{17\}\}\; -\; \{\backslash \; sqrt\; \{170\; +\; 38\; \{\backslash \; sqrt\; \{17\}\}\}\}\}\}.\; \backslash \; End\; \{align\}\}\}$

Конструкции для правильного треугольника, пятиугольник, пятиугольник и многоугольники с вдвое большим количеством сторон были даны Евклидом, но конструкции, основанные на простых числах Ферма, кроме 3 и 5, были неизвестны древним. (Единственные известные простые числа Ферма: F n для n = 0, 1, 2, 3, 4. Это 3, 5, 17, 257 и 65537.)

Явный Построение семиугольника было дано Гербертом Уильямом Ричмондом в 1893 году. Следующий метод построения использует круги Карлайла, как показано ниже. Основываясь на построении правильного 17-угольника, можно легко построить n-угольники, где n является произведением 17 на 3 или 5 (или и то, и другое) и любой степени двойки: правильный 51-угольник, 85-угольник или 255. -угольник и любой правильный n-угольник с числом сторон в 2 раза больше.

Построение по Дуэйну В. ДеТемплу с кругами Карлайла, анимация 1 мин 57 с

Еще одно построение правильного семиугольника с использованием линейки и циркуля:

T. П. Стоуэлл из Рочестера, штат Нью-Йорк, ответил на запрос W.E. Хил, Уилинг, Индиана в «Аналитике» в 1874 году:

«Чтобы построить правильный многоугольник из семнадцати сторон в окружности. Нарисуйте радиус CO под прямым углом к ​​диаметру AB: на OC и OB, возьмите OQ равным половине, а OD равным восьмой части радиуса: сделайте DE и DF равными DQ, а EG и FH, соответственно, равными EQ и FQ; примите OK как среднее, пропорциональное между OH и OQ, и через K, проведите KM параллельно AB, встречая полукруг, описанный на OG в M; проведите MN параллельно OC, разрезая данный круг в N - дуга AN является семнадцатой частью всей окружности ".

Построение в соответствии с. ", присланным Т.П. Стоуэллом, зачислено в Leybourn's Math. Repository, 1818".. Добавлено: "Хорошо, среднее пропорциональное между OH и OQ" Построение согласно. "прислано Т.П. Стоуэллом, зачислено в Leybourn's Math. Repository, 1818".. Добавлено: "Хорошо, среднее значение, пропорциональное между OH и OQ", анимация

Следующий простой проект принадлежит Герберту Уильям Ричмонд из 1893 года:

«Пусть OA, OB (рис. 6) будут двумя перпендикулярными радиусами окружности. Сделайте OI одной четвертой OB, а угол OIE - одной четвертой OIA; также найти в OA произвела точку F такую, что EIF составляет 45 °. Пусть окружность на AF как диаметр разрезает OB в K, и пусть окружность с центром в E и радиусом EK разрезает OA в N 3 и N 5 ; тогда, если ординаты N 3P3, N 5P5провести к окружности, то дуги AP 3, AP 5 будут 3/17 и 5 / 17 окружности ».

• Точка N 3 очень близка к центральной точке теоремы Фалеса над AF.

Constr Действие согласно H. W. Richmond Конструкция согласно H. W. Richmond как анимация

Следующая конструкция является вариацией конструкции H. W. Richmond.

Отличия от оригинала:

• Окружность k 2 определяет точку H вместо биссектрисы w 3.
• Окружность k 4 вокруг точки G '(отражение точки G в m) дает точку N, которая больше не так близка к M, для построения касательной.
• Некоторые названия были изменены.

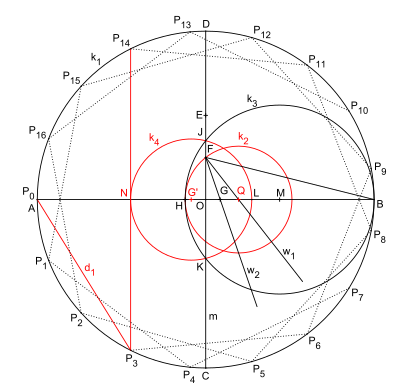Гептадекагон в принципе согласно HW Ричмонд, вариант конструкции относительно точки N

Другая более свежая конструкция дана Каллаги.

Симметрии правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. Порядки вращения даны в центре.

Правильный гептадекагон имеет Dih 17 симметрию, порядок 34. Поскольку 17 является простым числом, есть одна подгруппа с диэдральной симметрией: Dih 1 и 2 симметрии циклической группы : Z 17 и Z 1.

Эти 4 симметрии можно увидеть в 4 различных симметриях на гептадекагон. Джон Конвей помечает их буквой и групповым порядком. Полная симметрия правильной формы - r34, и никакая симметрия не помечена как a1 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины (d для диагонали) или ребра (p для перпендикуляров), и i, когда отражательные линии проходят через как ребра, так и вершины. Циклические симметрии в среднем столбце обозначены как g для их центральных порядков вращения.

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g17 не имеет степеней свободы, но может рассматриваться как направленные ребра.

Гептадекаграммы

Гептадекаграмма - это 17-сторонняя звездообразный многоугольник. Существует семь обычных форм, задаваемых символами Шлефли : {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7 } и {17/8}. Поскольку 17 - простое число, все это обычные звезды, а не составные числа.

Изображение	. {17/2}	. {17/3}	. {17/4}	. {17/5}	. {17/6}	. {17 / 7}	. {17/8}
Внутренний угол	≈137.647 °	≈116.471 °	≈95.2941 °	≈74.1176 °	≈52.9412 °	≈31.7647 °	≈10.5882 °

Многоугольники Петри

Правильный семиугольник - это многоугольник Петри для одного многомерного правильного выпуклого многогранника, спроецированного в наклонной ортогональной проекции :

. 16-симплекс (16D)

• Dunham, William (сентябрь 1996 г.). «1996 год - тройной юбилей». Math Horizons : 8–13. Проверено 6 декабря 2009 г.
• Klein, Felix et al. Известные проблемы и другие монографии. - Описывает алгебраический аспект, автор: Гаусс.

На Wikimedia Commons есть материалы, связанные с 17-угольниками.

• Вайсштейном, Эриком У. «Гептадекагон». MathWorld.Содержит описание конструкции.
• «Построение гептадекагона». MathPages.com.
• Тригонометрические функции Heptadecagon
• здание heptadecagon Новый центр исследований и разработок для SolarUK
• Видео BBC Нового центра исследований и разработок для SolarUK
• Эйзенбуд, Дэвид. «Удивительный гептадекагон (17-угольник)» (видео). Брэди Харан. Проверено 2 марта 2015 г.
• гептадекагон