Производная по направлению

редактировать

В математике, производная по направлению многомерной дифференцируемой функции вдоль заданного вектора vв заданной точке x интуитивно представляет мгновенную скорость изменения функции, перемещаясь через x со скоростью, заданной v . Следовательно, он обобщает понятие частной производной, в которой скорость изменения берется вдоль одной из криволинейных координатных кривых, все остальные координаты постоянны.

Производная по направлению является частным случаем производной Гато.

Содержание

1 Обозначение
2 Определение
- 2.1 Использование только направления вектора
- 2.2 Ограничение на единичный вектор
3 Свойства
4 В дифференциальной геометрии
- 4.1 Производная Ли
- 4.2 Тензор Римана
5 В теории групп
- 5.1 Сдвиги
- 5.2 Вращения
6 Нормаль производная
7 В сплошной механике твердого тела
- 7.1 Производные скалярных функций векторов
- 7.2 Производные векторных функций векторов
- 7.3 Производные скалярных функций от тензоров второго порядка
- 7.4 Производные тензорнозначных функций от тензоров второго порядка
8 См. Также
9 Примечания
10 Ссылки
11 Внешние ссылки

Обозначения

Пусть f будет кривая, касательный вектор которой в некоторой выбранной точке равен v . Производная по направлению функции f относительно v может быть обозначена любым из следующего:

$∇ vf (x), {\ displaystyle \ nabla _ {\ mathbf {v}} {f } (\ mathbf {x}),}$ $\nabla _{\mathbf {v} }{f}(\mathbf {x}),$
$fv ′ (x), {\ displaystyle f '_ {\ mathbf {v}} (\ mathbf {x}),}$ $f'_{\mathbf {v} }(\mathbf {x}),$
$D vf (x), {\ displaystyle D _ {\ mathbf {v}} f (\ mathbf {x}),}$ $D_{\mathbf {v} }f(\mathbf {x}),$
$D f (x) (v), {\ displaystyle Df (\ mathbf {x}) (\ mathbf {v}),}$ $Df(\mathbf {x})(\mathbf {v}),$
$∂ vf (x), {\ displaystyle \ partial _ {\ mathbf {v}} f (\ mathbf {x}),}$ $\partial _{\mathbf {v} }f(\mathbf {x}),$
$∂ f (x) ∂ v, {\ displaystyle { \ frac {\ partial {е (\ mathbf {x})}} {\ partial {\ mathbf {v}}}},}$ ${\frac {\partial {f(\mathbf {x})}}{\partial {\mathbf {v} }}},$
$v ⋅ ∇ f (x), {\ displaystyle \ mathbf {v} \ cdot {\ nabla f (\ mathbf {x})},}$ $\mathbf {v} \cdot {\nabla f(\mathbf {x})},$
$v ⋅ ∂ f (x) ∂ x. {\ displaystyle \ mathbf {v} \ cdot {\ frac {\ partial f (\ mathbf {x})} {\ partial \ mathbf {x}}}.}$ $\mathbf {v} \cdot {\frac {\partial f(\mathbf {x})}{\partial \mathbf {x} }}.$

Определение

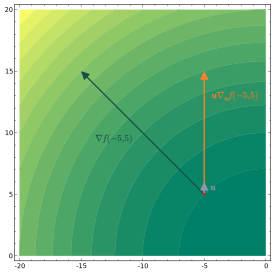
A контурный график из

f (x, y) = x 2 + y 2 {\ displaystyle f (x, y) = x ^ {2} + y ^ {2}}

f(x, y)=x^2 + y^2

, показывая вектор градиента черным цветом и единичный вектор

u {\ displaystyle \ mathbf {u}}

\mathbf {u}

, масштабированный производной по направлению в направлении

u {\ displaystyle \ mathbf {u}}

\mathbf {u}

оранжевым. Вектор градиента длиннее, потому что градиент указывает в направлении наибольшей скорости увеличения функции.

Производная по направлению скалярной функции

f (x) = f (x 1, x 2, …, Xn) {\ displaystyle f (\ mathbf {x}) = f (x_ {1}, x_ {2}, \ ldots, x_ {n})}

f(\mathbf {x})=f(x_{1},x_{2},\ldots,x_{n})

вдоль вектора

v = (v 1,…, vn) {\ displaystyle \ mathbf {v} = (v_ {1}, \ ldots, v_ {n})}

\mathbf {v} =(v_{1},\ldots,v_{n})

- это функция $∇ vf {\ displaystyle \ nabla _ {\ mathbf {v}} {f}}$ $\nabla _{\mathbf {v} }{f}$ определяется пределом

∇ vf (x) = lim h → 0 f (x + hv) - f (x) h. {\ displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ lim _ {h \ rightarrow 0} {\ frac {f (\ mathbf {x} + h \ mathbf {v }) -f (\ mathbf {x})} {h}}.}

\nabla _{\mathbf {v} }{f}(\mathbf {x})=\lim _{h\rightarrow 0}{\frac {f(\mathbf {x} +h\mathbf {v})-f(\mathbf {x})}{h}}.

Это определение действительно в широком диапазоне контекстов, например, когда norm вектора (и, следовательно, единичный вектор) не определен.

Если функция f дифференцируема в x, то производная по направлению существует вдоль любого вектора v, и один имеет

∇ vf (x) = ∇ е (x) ⋅ v {\ displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x }) \ cdot \ mathbf {v}}

\nabla _{\mathbf {v} }{f}(\mathbf {x})=\nabla f(\mathbf {x})\cdot \mathbf {v}

, где $∇ {\ displaystyle \ nabla}$ $\nabla$ справа обозначает градиент и $⋅ {\ displaystyle \ cdot}$ $\cdot$ - это скалярное произведение. Это следует из определения пути $h (t) = x + tv {\ displaystyle h (t) = x + tv}$ $h(t)=x+tv$ и использования определения производной в качестве предела, который может быть вычислен по этот путь получить:

0 = lim t → 0 f (x + tv) - f (x) - t D f (x) (v) t = lim t → 0 f (x + tv) - f ( х) t - D f (x) (v) = ∇ vf (x) - D f (x) (v) → ∇ f (x) ⋅ v = D f (x) (v) = ∇ vf (x) {\ displaystyle {\ begin {align} 0 = \ lim _ {t \ rightarrow 0} {\ frac {f (x + tv) -f (x) -tD_ {f} (x) (v)} {t} } = \ lim _ {t \ rightarrow 0} {\ frac {f (x + tv) -f (x)} {t}} - D_ {f} (x) (v) = \ nabla _ {v} f (x) -D_ {f} (x) (v) \\\ rightarrow \ nabla f (\ mathbf {x}) \ cdot \ mathbf {v} = D_ {f} (x) (v) = \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) \ end {align}}}

{\begin{aligned}0=\lim _{t\rightarrow 0}{\frac {f(x+tv)-f(x)-tD_{f}(x)(v)}{t}}=\lim _{t\rightarrow 0}{\frac {f(x+tv)-f(x)}{t}}-D_{f}(x)(v)=\nabla _{v}f(x)-D_{f}(x)(v)\\\rightarrow \nabla f(\mathbf {x})\cdot \mathbf {v} =D_{f}(x)(v)=\nabla _{\mathbf {v} }{f}(\mathbf {x})\end{aligned}}

Интуитивно понятно, что производная f по направлению в точке x представляет скорость изменения f, в направлении v относительно времени, при движении мимо x.

Использование только направления вектора

Угол α между касательной A и горизонталью будет максимум, если t Режущая плоскость содержит направление градиента A.

В евклидовом пространстве некоторые авторы определяют производную по направлению как относящуюся к произвольному ненулевому вектору v после нормализация, поэтому она не зависит от ее величины и зависит только от ее направления.

Это определение дает скорость увеличения f на единицу расстояния, перемещенного в направлении, заданном как v . В этом случае

∇ v f (x) = lim h → 0 f (x + h v) - f (x) h | v |, {\ displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ lim _ {h \ rightarrow 0} {\ frac {f (\ mathbf {x} + h \ mathbf { v}) -f (\ mathbf {x})} {h | \ mathbf {v} |}},}

\nabla _{\mathbf {v} }{f}(\mathbf {x})=\lim _{h\rightarrow 0}{\frac {f(\mathbf {x} +h\mathbf {v})-f(\mathbf {x})}{h|\mathbf {v} |}},

или в случае, если f дифференцируема в x,

∇ vf (x) = ∇ f (x) ⋅ v | v |. {\ displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x}) \ cdot {\ frac {\ mathbf {v}} {| \ mathbf {v} |}}.}

\nabla _{\mathbf {v} }{f}(\mathbf {x})=\nabla f(\mathbf {x})\cdot {\frac {\mathbf {v} }{|\mathbf {v} |}}.

Ограничение на единичный вектор

В контексте функции в евклидовом пространстве некоторые тексты ограничивают вектор v в единичный вектор. С этим ограничением оба приведенных выше определения эквивалентны.

Свойства

Многие из знакомых свойств обычной производной сохраняются для производной по направлению. К ним относятся, для любых функций f и g, определенных в окрестности из и дифференцируемой at, p:

правило сумм :
$∇ v (f + g) = ∇ vf + ∇ vg. {\ displaystyle \ nabla _ {\ mathbf {v}} (f + g) = \ nabla _ {\ mathbf {v}} f + \ nabla _ {\ mathbf {v}} g.}$ $\nabla _{\mathbf {v} }(f+g)=\nabla _{\mathbf {v} }f+\nabla _{\mathbf {v} }g.$
правило постоянного множителя : для любой константы c
$∇ v (cf) = c ∇ vf. {\ displaystyle \ nabla _ {\ mathbf {v}} (cf) = c \ nabla _ {\ mathbf {v}} f.}$ $\nabla _{\mathbf {v} }(cf)=c\nabla _{\mathbf {v} }f.$
правило продукта (или правило Лейбница ):
$∇ v (fg) = g ∇ vf + f ∇ vg. {\ displaystyle \ nabla _ {\ mathbf {v}} (fg) = g \ nabla _ {\ mathbf {v}} f + f \ nabla _ {\ mathbf {v}} g.}$ $\nabla _{\mathbf {v} }(fg)=g\nabla _{\mathbf {v} }f+f\nabla _{\mathbf {v} }g.$
правило цепочки : Если g дифференцируема в p и h дифференцируема в g (p ), то
$∇ v (h ∘ g) (p) = h ′ (g (p)) ∇ vg (p). {\ displaystyle \ nabla _ {\ mathbf {v}} (h \ circ g) (\ mathbf {p}) = h '(g (\ mathbf {p})) \ nabla _ {\ mathbf {v}} g (\ mathbf {p}).}$ $\nabla _{\mathbf {v} }(h\circ g)(\mathbf {p})=h'(g(\mathbf {p}))\nabla _{\mathbf {v} }g(\mathbf {p}).$

В дифференциальной геометрии

Пусть M будет дифференцируемым многообразием и p точкой M. Предположим, что f является функция, определенная в окрестности p, и дифференцируемая в p . Если v является касательным вектором к M в p, то производная по направлению f вдоль v, обозначается по-разному как df (v ) (см. Внешняя производная ), $∇ vf (p) {\ displaystyle \ nabla _ {\ mathbf {v}} f (\ mathbf {p})}$ $\nabla _{\mathbf {v} }f(\mathbf {p})$ (см. Ковариантная производная ), $L vf (p) {\ displaystyle L _ {\ mathbf {v}} f (\ mathbf {p}) }$ $L_{\mathbf {v} }f(\mathbf {p})$ (см. производная Ли ) или $vp (f) {\ displaystyle {\ mathbf {v}} _ {\ mathbf {p}} (f)}$ ${\mathbf {v} }_{\mathbf {p} }(f)$ (см. Касательное пространство § Определение посредством производных ), можно определить следующим образом. Пусть γ: [−1, 1] → M - дифференцируемая кривая с γ (0) = p и γ ′ (0) = v . Тогда производная по направлению определяется выражением

∇ v f (p) = d d τ f γ (τ) | τ = 0. {\ displaystyle \ nabla _ {\ mathbf {v}} f (\ mathbf {p}) = \ left. {\ frac {d} {d \ tau}} f \ circ \ gamma (\ tau) \ right | _ {\ tau = 0}.}

\nabla _{\mathbf {v} }f(\mathbf {p})=\left.{\frac {d}{d\tau }}f\circ \gamma (\tau)\right|_{\tau =0}.

Это определение может быть доказано независимо от выбора γ, при условии, что γ выбрано предписанным образом, так что γ ′ (0) = v.

Производная Ли

Производная Ли векторного поля $W μ (x) {\ displaystyle \ scriptstyle W ^ {\ mu} (x)}$ $\scriptstyle W^\mu(x)$ вдоль векторного поля $V μ (x) {\ displaystyle \ scriptstyle V ^ {\ mu} (x)}$ $\scriptstyle V^\mu(x)$ дается разностью двух производных по направлению (с нулевым кручением):

LVW μ = (V ⋅ ∇) W μ - (W ⋅ ∇) V μ. {\ displaystyle {\ mathcal {L}} _ {V} W ^ {\ mu} = (V \ cdot \ nabla) W ^ {\ mu} - (W \ cdot \ nabla) V ^ {\ mu}.}

{\mathcal {L}}_{V}W^{\mu }=(V\cdot \nabla)W^{\mu }-(W\cdot \nabla)V^{\mu }.

В частности, для скалярного поля $ϕ (x) {\ displaystyle \ scriptstyle \ phi (x)}$ $\scriptstyle \phi(x)$ производная Ли сводится к стандартной производной по направлению:

LV ϕ = (V ⋅ ∇) ϕ. {\ displaystyle {\ mathcal {L}} _ {V} \ phi = (V \ cdot \ nabla) \ phi.}

{\mathcal {L}}_{V}\phi =(V\cdot \nabla)\phi.

Тензор Римана

Производные по направлениям часто используются во вводных выводах Тензор кривизны Римана. Рассмотрим изогнутый прямоугольник с бесконечно малым вектором δ по одному краю и δ ′ по другому. Мы переносим ковектор S вдоль δ, затем вдоль δ ′, затем вычитаем перенос вдоль δ ′ и затем δ. Вместо построения производной по направлению с использованием частных производных мы используем ковариантную производную. Таким образом, оператор перевода для δ имеет вид

1 + ∑ ν δ ν D ν = 1 + δ ⋅ D, {\ displaystyle 1+ \ sum _ {\ nu} \ delta ^ {\ nu} D _ {\ nu} = 1+ \ delta \ cdot D,}

1+\sum _{\nu }\delta ^{\nu }D_{\nu }=1+\delta \cdot D,

и для δ ′

1 + ∑ μ δ ′ μ D μ = 1 + δ ′ ⋅ D. {\ displaystyle 1+ \ sum _ {\ mu} \ delta '^ {\ mu} D _ {\ mu} = 1 + \ delta' \ cdot D.}

1+\sum _{\mu }\delta '^{\mu }D_{\mu }=1+\delta '\cdot D.

Тогда разница между двумя путями составляет

(1 + δ ′ ⋅ D) (1 + δ ⋅ D) S ρ - (1 + δ ⋅ D) (1 + δ ′ ⋅ D) S ρ = ∑ μ, ν δ ′ μ δ ν [D μ, D ν] S ρ. {\ displaystyle (1+ \ delta '\ cdot D) (1+ \ delta \ cdot D) S ^ {\ rho} - (1+ \ delta \ cdot D) (1+ \ delta' \ cdot D) S ^ {\ rho} = \ sum _ {\ mu, \ nu} \ delta '^ {\ mu} \ delta ^ {\ nu} [D _ {\ mu}, D _ {\ nu}] S _ {\ rho}.}

(1+\delta '\cdot D)(1+\delta \cdot D)S^{\rho }-(1+\delta \cdot D)(1+\delta '\cdot D)S^{\rho }=\sum _{\mu,\nu }\delta '^{\mu }\delta ^{\nu }[D_{\mu },D_{\nu }]S_{\rho }.

Можно утверждать, что некоммутативность ковариантных производных измеряет кривизну многообразия:

[D μ, D ν] S ρ = ± ∑ σ R σ ρ μ ν S σ, {\ displaystyle [D_ {\ mu}, D _ {\ nu}] S _ {\ rho} = \ pm \ sum _ {\ sigma} R ^ {\ sigma} {} _ {\ rho \ mu \ nu} S _ {\ sigma},}

[D_{\mu },D_{\nu }]S_{\rho }=\pm \sum _{\sigma }R^{\sigma }{}_{\rho \mu \nu }S_{\sigma },

где R - тензор кривизны Римана, а знак зависит от соглашения о знаках автора.

В теории групп

Переводы

В алгебре Пуанкаре мы можем определить оператор инфинитезимального преобразования P как

P = i ∇. {\ displaystyle \ mathbf {P} = i \ nabla.}

\mathbf {P} =i\nabla.

(i гарантирует, что P является самосопряженным оператором ) Для конечного смещения λ, унитарное гильбертово пространство представление для переводов равно

U (λ) = exp ⁡ (- i λ ⋅ P). {\ displaystyle U (\ mathbf {\ lambda}) = \ exp \ left (-i \ mathbf {\ lambda} \ cdot \ mathbf {P} \ right).}

U(\mathbf {\lambda })=\exp \left(-i\mathbf {\lambda } \cdot \mathbf {P} \right).

Используя приведенное выше определение бесконечно малого преобразования, мы видим, что оператор конечного сдвига является экспоненциальной производной по направлению:

U (λ) = exp ⁡ (λ ⋅ ∇). {\ displaystyle U (\ mathbf {\ lambda}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right).}

U(\mathbf {\lambda })=\exp \left(\mathbf {\lambda } \cdot \nabla \right).

Это оператор перевода в том смысле, что он действует на функции с несколькими переменными f (x ) как

U (λ) f (x) = exp ⁡ (λ ⋅ ∇) f (x) = f (x + λ). {\ Displaystyle U (\ mathbf {\ lambda}) f (\ mathbf {x}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right) f (\ mathbf {x}) = f ( \ mathbf {x} + \ mathbf {\ lambda}).}

U(\mathbf {\lambda })f(\mathbf {x})=\exp \left(\mathbf {\lambda } \cdot \nabla \right)f(\mathbf {x})=f(\mathbf {x} +\mathbf {\lambda }).

Доказательство последнего уравнения
В стандартном исчислении с одной переменной производная гладкой функции f (x) определяется как (для малых ε) $dfdx = f (x + ϵ) - f (x) ϵ. {\ displaystyle {\ frac {df} {dx}} = {\ frac {f (x + \ epsilon) -f (x)} {\ epsilon}}.}$ ${\frac {df}{dx}}={\frac {f(x+\epsilon)-f(x)}{\epsilon }}.$ Это можно изменить, чтобы найти f (x + ε): $f (x + ϵ) = f (x) + ϵ dfdx = (1 + ϵ ddx) f (x). {\ displaystyle f (x + \ epsilon) = f (x) + \ epsilon \, {\ frac {df} {dx}} = \ left (1+ \ epsilon \, {\ frac {d} {dx}} \ справа) f (x).}$ $f(x+\epsilon)=f(x)+\epsilon \,{\frac {df}{dx}}=\left(1+\epsilon \,{\frac {d}{dx}}\right)f(x).$ Отсюда следует, что $[1 + ϵ (d / dx)] {\ displaystyle [1+ \ epsilon \, (d / dx)]}$ $[1+\epsilon\,(d/dx)]$ оператор перевода. Это мгновенно обобщается на функции многих переменных f (x) $f (x + ϵ) = (1 + ϵ ⋅ ∇) f (x). {\ Displaystyle f (\ mathbf {x} + \ mathbf {\ epsilon}) = \ left (1+ \ mathbf {\ epsilon} \ cdot \ nabla \ right) f (\ mathbf {x}).}$ $f(\mathbf {x} +\mathbf {\epsilon })=\left(1+\mathbf {\epsilon } \cdot \nabla \right)f(\mathbf {x}).$ Здесь $ϵ ⋅ ∇ {\ displaystyle \ mathbf {\ epsilon} \ cdot \ nabla}$ $\mathbf {\epsilon } \cdot \nabla$ - производная по направлению вдоль бесконечно малого смещения ε . Мы нашли бесконечно малую версию оператора перевода: $U (ϵ) = 1 + ϵ ⋅ ∇. { \ Displaystyle U (\ mathbf {\ epsilon}) = 1 + \ mathbf {\ epsilon} \ cdot \ nabla.}$ $U(\mathbf {\epsilon })=1+\mathbf {\epsilon } \cdot \nabla.$ Очевидно, что закон группового умножения U (g) U (f) = U (gf) принимает форму $U (a) U (b) = U (a + b). {\ displaystyle U (\ mathbf {a}) U (\ mathbf {b}) = U (\ mathbf {a + b }).}$ $U(\mathbf {a})U(\mathbf {b})=U(\mathbf {a+b}).$ Итак, предположим, что мы берем конечное смещение λ и делим его на N частей (везде подразумевается N → ∞), так что λ / N = ε . Другими словами, $λ = N ϵ. {\ Displaystyle \ mathbf {\ lambda} = N \ mathbf {\ epsilon}.}$ $\mathbf {\lambda } =N\mathbf {\epsilon }.$ Затем через ap Используя U (ε ) N раз, мы можем построить U (λ ): $[U (ϵ)] N = U (N ϵ) = U (λ). {\ displaystyle [U (\ mathbf {\ epsilon})] ^ {N} = U (N \ mathbf {\ epsilon}) = U (\ mathbf {\ lambda}).}$ $[U(\mathbf {\epsilon })]^{N}=U(N\mathbf {\epsilon })=U(\mathbf {\lambda }).$ Теперь мы можем подключить наш приведенное выше выражение для U (ε ): $[U (ϵ)] N = [1 + ϵ ⋅ ∇] N = [1 + λ ⋅ N] N. {\ Displaystyle [U (\ mathbf {\ epsilon})] ^ {N} = \ left [1+ \ mathbf {\ epsilon} \ cdot \ nabla \ right] ^ {N} = \ left [1 + {\ frac {\ mathbf {\ lambda} \ cdot \ nabla} {N}} \ right] ^ {N}.}$ $[U(\mathbf {\epsilon })]^{N}=\left[1+\mathbf {\epsilon } \cdot \nabla \right]^{N}=\left[1+{\frac {\mathbf {\lambda } \cdot \nabla }{N}}\right]^{N}.$ Использование тождества $exp ⁡ (x) = [1 + x N] N, {\ displaystyle \ exp (x) = \ left [1 + {\ frac {x} {N}} \ right] ^ {N},}$ $\exp(x)=\left[1+{\frac {x}{N}}\right]^{N},$ мы имеем $U (λ) = exp ⁡ (λ ⋅ ∇). {\ displaystyle U (\ mathbf {\ lambda}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right).}$ $U(\mathbf {\lambda })=\exp \left(\mathbf {\lambda } \cdot \nabla \right).$ И поскольку U (ε ) f ( x ) = f (x+ε) имеем $[U (ϵ)] N f (x) = f (x + N ϵ) = f (x + λ) = U (λ) е (Икс) знак равно ехр ⁡ (λ ⋅ ∇) е (Икс), {\ Displaystyle [U (\ mathbf {\ epsilon})] ^ {N} е (\ mathbf {x}) = F (\ mathbf { x} + N \ mathbf {\ epsilon}) = f (\ mathbf {x} + \ mathbf {\ lambda}) = U (\ mathbf {\ lambda}) f (\ mathbf {x}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right) f (\ mathbf {x}),}$ $[U(\mathbf {\epsilon })]^{N}f(\mathbf {x})=f(\mathbf {x} +N\mathbf {\epsilon })=f(\mathbf {x} +\mathbf {\lambda })=U(\mathbf {\lambda })f(\mathbf {x})=\exp \left(\mathbf {\lambda } \cdot \nabla \right)f(\mathbf {x}),$ QED В качестве технического примечания эта процедура возможна только потому, что группа трансляций образует абелевскую подгруппу (подалгебра Картана ) в алгебре Пуанкаре.. В частности, закон группового умножения U (a ) U (b ) = U (a+b) не следует принимать как должное. Отметим также, что Пуанкаре - связная группа Ли. Это группа преобразований T (ξ), которые описываются непрерывным набором реальных параметров $ξ a {\ displaystyle \ scriptstyle \ xi ^ {a}}$ $\scriptstyle \xi^a$ . Закон группового умножения принимает вид $T (ξ ¯) T (ξ) = T (f (ξ ¯, ξ)). {\ displaystyle T ({\ bar {\ xi}}) T (\ xi) = T (f ({\ bar {\ xi}}, \ xi)).}$ $T({\bar {\xi }})T(\xi)=T(f({\bar {\xi }},\xi)).$ Принимая $ξ a {\ displaystyle \ scriptstyle \ xi ^ {a}}$ $\scriptstyle \xi^a$ = 0 в качестве координат идентичности, мы должны иметь $fa (ξ, 0) = fa (0, ξ) = ξ a. {\ displaystyle f ^ {a} (\ xi, 0) = f ^ {a} (0, \ xi) = \ xi ^ {a}.}$ $f^{a}(\xi,0)=f^{a}(0,\xi)=\xi ^{a}.$ Фактические операторы в гильбертовом пространстве представлены унитарными операторами U (T (ξ)). В приведенных выше обозначениях мы убрали T; теперь запишем U (λ ) как U (P(λ)). Для небольшой окрестности вокруг идентичности представление степенного ряда $U (T (ξ)) = 1 + i ∑ a ξ ata + 1 2 ∑ b, c ξ b ξ ctbc + ⋯ {\ displaystyle U (T ( \ xi)) = 1 + i \ sum _ {a} \ xi ^ {a} t_ {a} + {\ frac {1} {2}} \ sum _ {b, c} \ xi ^ {b} \ xi ^ {c} t_ {bc} + \ cdots}$ $U(T(\xi))=1+i\sum_a\xi^a t_a+\frac{1}{2}\sum_{b,c}\xi^b\xi^c t_{bc}+\cdots$ неплохо. Предположим, что U (T (ξ)) образуют непроективное представление, т. Е. $U (T (ξ ¯)) U (T (ξ)) = U (T (f (ξ ¯, ξ))). {\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T (F ({\ bar {\ xi}}, \ xi))).}$ $U(T({\bar {\xi }}))U(T(\xi))=U(T(f({\bar {\xi }},\xi))).$ Разложение f во вторую степень равно $fa (ξ ¯, ξ) = ξ a + ξ ¯ a + ∑ b, cfabc ξ ¯ b ξ c. {\ displaystyle f ^ {a} ({\ bar {\ xi}}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a} + \ sum _ {b, c} f ^ {abc} {\ bar {\ xi}} ^ {b} \ xi ^ {c}.}$ $f^{a}({\bar {\xi }},\xi)=\xi ^{a}+{\bar {\xi }}^{a}+\sum _{b,c}f^{abc}{\bar {\xi }}^{b}\xi ^{c}.$ После расширения уравнения умножения представления и приравнивания коэффициентов мы получаем нетривиальное условие $tbc = - tbtc - я afabcta. {\ displaystyle t_ {bc} = - t_ {b} t_ {c} -i \ sum _ {a} f ^ {abc} t_ {a}.}$ $t_{bc}=-t_{b}t_{c}-i\sum _{a}f^{abc}t_{a}.$ Поскольку $tab {\ displaystyle \ scriptstyle t_ {ab}}$ $\scriptstyle t_{ab}$ по определению симметричен по своим индексам, у нас есть стандартный коммутатор алгебры Ли : $[tb, tc] = i ∑ a (- fabc + facb) та знак равно я ∑ a C abcta, {\ displaystyle [t_ {b}, t_ {c}] = i \ sum _ {a} (- f ^ {abc} + f ^ {acb}) t_ {a} = i \ sum _ {a} C ^ {abc} t_ {a},}$ $[t_{b},t_{c}]=i\sum _{a}(-f^{abc}+f^{acb})t_{a}=i\sum _{a}C^{abc}t_{a},$ , где C - структурная константа . Генераторами для переводов являются операторы частных производных, которые коммутируют: $[∂ ∂ xb, ∂ ∂ xc] = 0. {\ displaystyle \ left [{\ frac {\ partial} {\ partial x ^ {b}}}, {\ frac {\ partial} {\ partial x ^ {c}}} \ right] = 0.}$ $\left[{\frac {\partial }{\partial x^{b}}},{\frac {\partial }{\partial x^{c}}}\right]=0.$ Это означает, что структурные константы обращаются в нуль и, следовательно, равны нулю и квадратичные коэффициенты в разложении f. Это означает, что f просто аддитивно: $f абелева a (ξ ¯, ξ) = ξ a + ξ ¯ a, {\ displaystyle f _ {\ text {abelian}} ^ {a} ({\ bar {\ xi }}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a},}$ $f_{\text{abelian}}^{ a}({\bar {\xi }},\xi)=\xi ^{a}+{\bar {\xi }}^{a},$ и, следовательно, для абелевых групп $U (T (ξ ¯)) U ( T (ξ)) = U (T (ξ ¯ + ξ)). {\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T ({\ bar {\ xi}} + \ xi)).}$ $U(T({\bar {\xi }}))U(T(\xi))=U(T({\bar {\xi }}+\xi)).$ Q.E.D.

Доказательство последнего уравнения

В стандартном исчислении с одной переменной производная гладкой функции f (x) определяется как (для малых ε)

dfdx = f (x + ϵ) - f (x) ϵ. {\ displaystyle {\ frac {df} {dx}} = {\ frac {f (x + \ epsilon) -f (x)} {\ epsilon}}.}

{\frac {df}{dx}}={\frac {f(x+\epsilon)-f(x)}{\epsilon }}.

Это можно изменить, чтобы найти f (x + ε):

f (x + ϵ) = f (x) + ϵ dfdx = (1 + ϵ ddx) f (x). {\ displaystyle f (x + \ epsilon) = f (x) + \ epsilon \, {\ frac {df} {dx}} = \ left (1+ \ epsilon \, {\ frac {d} {dx}} \ справа) f (x).}

f(x+\epsilon)=f(x)+\epsilon \,{\frac {df}{dx}}=\left(1+\epsilon \,{\frac {d}{dx}}\right)f(x).

Отсюда следует, что $[1 + ϵ (d / dx)] {\ displaystyle [1+ \ epsilon \, (d / dx)]}$ $[1+\epsilon\,(d/dx)]$ оператор перевода. Это мгновенно обобщается на функции многих переменных f (x)

f (x + ϵ) = (1 + ϵ ⋅ ∇) f (x). {\ Displaystyle f (\ mathbf {x} + \ mathbf {\ epsilon}) = \ left (1+ \ mathbf {\ epsilon} \ cdot \ nabla \ right) f (\ mathbf {x}).}

f(\mathbf {x} +\mathbf {\epsilon })=\left(1+\mathbf {\epsilon } \cdot \nabla \right)f(\mathbf {x}).

Здесь $ϵ ⋅ ∇ {\ displaystyle \ mathbf {\ epsilon} \ cdot \ nabla}$ $\mathbf {\epsilon } \cdot \nabla$ - производная по направлению вдоль бесконечно малого смещения ε . Мы нашли бесконечно малую версию оператора перевода:

U (ϵ) = 1 + ϵ ⋅ ∇. { \ Displaystyle U (\ mathbf {\ epsilon}) = 1 + \ mathbf {\ epsilon} \ cdot \ nabla.}

U(\mathbf {\epsilon })=1+\mathbf {\epsilon } \cdot \nabla.

Очевидно, что закон группового умножения U (g) U (f) = U (gf) принимает форму

U (a) U (b) = U (a + b). {\ displaystyle U (\ mathbf {a}) U (\ mathbf {b}) = U (\ mathbf {a + b }).}

U(\mathbf {a})U(\mathbf {b})=U(\mathbf {a+b}).

Итак, предположим, что мы берем конечное смещение λ и делим его на N частей (везде подразумевается N → ∞), так что λ / N = ε . Другими словами,

λ = N ϵ. {\ Displaystyle \ mathbf {\ lambda} = N \ mathbf {\ epsilon}.}

\mathbf {\lambda } =N\mathbf {\epsilon }.

Затем через ap Используя U (ε ) N раз, мы можем построить U (λ ):

[U (ϵ)] N = U (N ϵ) = U (λ). {\ displaystyle [U (\ mathbf {\ epsilon})] ^ {N} = U (N \ mathbf {\ epsilon}) = U (\ mathbf {\ lambda}).}

[U(\mathbf {\epsilon })]^{N}=U(N\mathbf {\epsilon })=U(\mathbf {\lambda }).

Теперь мы можем подключить наш приведенное выше выражение для U (ε ):

[U (ϵ)] N = [1 + ϵ ⋅ ∇] N = [1 + λ ⋅ N] N. {\ Displaystyle [U (\ mathbf {\ epsilon})] ^ {N} = \ left [1+ \ mathbf {\ epsilon} \ cdot \ nabla \ right] ^ {N} = \ left [1 + {\ frac {\ mathbf {\ lambda} \ cdot \ nabla} {N}} \ right] ^ {N}.}

[U(\mathbf {\epsilon })]^{N}=\left[1+\mathbf {\epsilon } \cdot \nabla \right]^{N}=\left[1+{\frac {\mathbf {\lambda } \cdot \nabla }{N}}\right]^{N}.

Использование тождества

exp ⁡ (x) = [1 + x N] N, {\ displaystyle \ exp (x) = \ left [1 + {\ frac {x} {N}} \ right] ^ {N},}

\exp(x)=\left[1+{\frac {x}{N}}\right]^{N},

мы имеем

U (λ) = exp ⁡ (λ ⋅ ∇). {\ displaystyle U (\ mathbf {\ lambda}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right).}

U(\mathbf {\lambda })=\exp \left(\mathbf {\lambda } \cdot \nabla \right).

И поскольку U (ε ) f ( x ) = f (x+ε) имеем

[U (ϵ)] N f (x) = f (x + N ϵ) = f (x + λ) = U (λ) е (Икс) знак равно ехр ⁡ (λ ⋅ ∇) е (Икс), {\ Displaystyle [U (\ mathbf {\ epsilon})] ^ {N} е (\ mathbf {x}) = F (\ mathbf { x} + N \ mathbf {\ epsilon}) = f (\ mathbf {x} + \ mathbf {\ lambda}) = U (\ mathbf {\ lambda}) f (\ mathbf {x}) = \ exp \ left (\ mathbf {\ lambda} \ cdot \ nabla \ right) f (\ mathbf {x}),}

[U(\mathbf {\epsilon })]^{N}f(\mathbf {x})=f(\mathbf {x} +N\mathbf {\epsilon })=f(\mathbf {x} +\mathbf {\lambda })=U(\mathbf {\lambda })f(\mathbf {x})=\exp \left(\mathbf {\lambda } \cdot \nabla \right)f(\mathbf {x}),

QED

В качестве технического примечания эта процедура возможна только потому, что группа трансляций образует абелевскую подгруппу (подалгебра Картана ) в алгебре Пуанкаре.. В частности, закон группового умножения U (a ) U (b ) = U (a+b) не следует принимать как должное. Отметим также, что Пуанкаре - связная группа Ли. Это группа преобразований T (ξ), которые описываются непрерывным набором реальных параметров $ξ a {\ displaystyle \ scriptstyle \ xi ^ {a}}$ $\scriptstyle \xi^a$ . Закон группового умножения принимает вид

T (ξ ¯) T (ξ) = T (f (ξ ¯, ξ)). {\ displaystyle T ({\ bar {\ xi}}) T (\ xi) = T (f ({\ bar {\ xi}}, \ xi)).}

T({\bar {\xi }})T(\xi)=T(f({\bar {\xi }},\xi)).

Принимая $ξ a {\ displaystyle \ scriptstyle \ xi ^ {a}}$ $\scriptstyle \xi^a$ = 0 в качестве координат идентичности, мы должны иметь

fa (ξ, 0) = fa (0, ξ) = ξ a. {\ displaystyle f ^ {a} (\ xi, 0) = f ^ {a} (0, \ xi) = \ xi ^ {a}.}

f^{a}(\xi,0)=f^{a}(0,\xi)=\xi ^{a}.

Фактические операторы в гильбертовом пространстве представлены унитарными операторами U (T (ξ)). В приведенных выше обозначениях мы убрали T; теперь запишем U (λ ) как U (P(λ)). Для небольшой окрестности вокруг идентичности представление степенного ряда

U (T (ξ)) = 1 + i ∑ a ξ ata + 1 2 ∑ b, c ξ b ξ ctbc + ⋯ {\ displaystyle U (T ( \ xi)) = 1 + i \ sum _ {a} \ xi ^ {a} t_ {a} + {\ frac {1} {2}} \ sum _ {b, c} \ xi ^ {b} \ xi ^ {c} t_ {bc} + \ cdots}

U(T(\xi))=1+i\sum_a\xi^a t_a+\frac{1}{2}\sum_{b,c}\xi^b\xi^c t_{bc}+\cdots

неплохо. Предположим, что U (T (ξ)) образуют непроективное представление, т. Е.

U (T (ξ ¯)) U (T (ξ)) = U (T (f (ξ ¯, ξ))). {\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T (F ({\ bar {\ xi}}, \ xi))).}

U(T({\bar {\xi }}))U(T(\xi))=U(T(f({\bar {\xi }},\xi))).

Разложение f во вторую степень равно

fa (ξ ¯, ξ) = ξ a + ξ ¯ a + ∑ b, cfabc ξ ¯ b ξ c. {\ displaystyle f ^ {a} ({\ bar {\ xi}}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a} + \ sum _ {b, c} f ^ {abc} {\ bar {\ xi}} ^ {b} \ xi ^ {c}.}

f^{a}({\bar {\xi }},\xi)=\xi ^{a}+{\bar {\xi }}^{a}+\sum _{b,c}f^{abc}{\bar {\xi }}^{b}\xi ^{c}.

После расширения уравнения умножения представления и приравнивания коэффициентов мы получаем нетривиальное условие

tbc = - tbtc - я afabcta. {\ displaystyle t_ {bc} = - t_ {b} t_ {c} -i \ sum _ {a} f ^ {abc} t_ {a}.}

t_{bc}=-t_{b}t_{c}-i\sum _{a}f^{abc}t_{a}.

Поскольку $tab {\ displaystyle \ scriptstyle t_ {ab}}$ $\scriptstyle t_{ab}$ по определению симметричен по своим индексам, у нас есть стандартный коммутатор алгебры Ли :

[tb, tc] = i ∑ a (- fabc + facb) та знак равно я ∑ a C abcta, {\ displaystyle [t_ {b}, t_ {c}] = i \ sum _ {a} (- f ^ {abc} + f ^ {acb}) t_ {a} = i \ sum _ {a} C ^ {abc} t_ {a},}

[t_{b},t_{c}]=i\sum _{a}(-f^{abc}+f^{acb})t_{a}=i\sum _{a}C^{abc}t_{a},

, где C - структурная константа . Генераторами для переводов являются операторы частных производных, которые коммутируют:

[∂ ∂ xb, ∂ ∂ xc] = 0. {\ displaystyle \ left [{\ frac {\ partial} {\ partial x ^ {b}}}, {\ frac {\ partial} {\ partial x ^ {c}}} \ right] = 0.}

\left[{\frac {\partial }{\partial x^{b}}},{\frac {\partial }{\partial x^{c}}}\right]=0.

Это означает, что структурные константы обращаются в нуль и, следовательно, равны нулю и квадратичные коэффициенты в разложении f. Это означает, что f просто аддитивно:

f абелева a (ξ ¯, ξ) = ξ a + ξ ¯ a, {\ displaystyle f _ {\ text {abelian}} ^ {a} ({\ bar {\ xi }}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a},}

f_{\text{abelian}}^{ a}({\bar {\xi }},\xi)=\xi ^{a}+{\bar {\xi }}^{a},

и, следовательно, для абелевых групп

U (T (ξ ¯)) U ( T (ξ)) = U (T (ξ ¯ + ξ)). {\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T ({\ bar {\ xi}} + \ xi)).}

U(T({\bar {\xi }}))U(T(\xi))=U(T({\bar {\xi }}+\xi)).

Q.E.D.

Вращения

Оператор вращения также содержит производную по направлению. Оператор поворота для угла θ, то есть на величину θ = | θ | вокруг оси, параллельной $θ ^ {\ displaystyle \ scriptstyle {\ hat {\ theta}}}$ $\scriptstyle \hat{\theta}$ = θ/ θ равно

U (R (θ)) = exp ⁡ (- i θ ⋅ L). {\ displaystyle U (R (\ mathbf {\ theta})) = \ exp (-i \ mathbf {\ theta} \ cdot \ mathbf {L}).}

U(R(\mathbf {\theta }))=\exp(-i\mathbf {\theta } \cdot \mathbf {L}).

Здесь L - это векторный оператор, который генерирует SO (3) :

L = (0 0 0 0 0 1 0 - 1 0) i + (0 0 - 1 0 0 0 1 0 0) j + (0 1 0 - 1 0 0 0 0 0) к. {\ displaystyle \ mathbf {L} = {\ begin {pmatrix} 0 0 0 \\ 0 0 1 \\ 0 -1 0 \ end {pmatrix}} \ mathbf {i} + {\ begin {pmatrix} 0 0 -1 \\ 0 0 0 \\ 1 0 0 \ end {pmatrix}} \ mathbf {j} + {\ begin {pmatrix} 0 1 0 \\ - 1 0 0 \\ 0 0 0 \ end {pmatrix}} \ mathbf {k}.}

\mathbf {L} ={\begin{pmatrix}000\\001\\0-10\end{pmatrix}}\mathbf {i} +{\begin{pmatrix}00-1\\000\\100\end{pmatrix}}\mathbf {j} +{\begin{pmatrix}010\\-100\\000\end{pmatrix}}\mathbf {k}.

Геометрически можно показать, что бесконечно малое правое вращение изменяет вектор положения x на

x → x - δ θ × x. {\ displaystyle \ mathbf {x} \ rightarrow \ mathbf {x} - \ delta \ mathbf {\ theta} \ times \ mathbf {x}.}

\mathbf {x} \rightarrow \mathbf {x} -\delta \mathbf {\theta } \times \mathbf {x}.

Таким образом, при бесконечно малом вращении мы ожидаем:

U (R (δ θ)) f (x) = f (x - δ θ × x) = f (x) - (δ θ × x) ⋅ ∇ f. {\ Displaystyle U (р (\ дельта \ mathbf {\ theta})) е (\ mathbf {x}) = f (\ mathbf {x} - \ delta \ mathbf {\ theta} \ times \ mathbf {x}) = f (\ mathbf {x}) - (\ delta \ mathbf {\ theta} \ times \ mathbf {x}) \ cdot \ nabla f.}

U(R(\delta \mathbf {\theta }))f(\mathbf {x})=f(\mathbf {x} -\delta \mathbf {\theta } \times \mathbf {x})=f(\mathbf {x})-(\delta \mathbf {\theta } \times \mathbf {x})\cdot \nabla f.

Отсюда следует, что

U (R (δ θ)) = 1 - (δ θ × x) ⋅ ∇. {\ displaystyle U (R (\ delta \ mathbf {\ theta})) = 1 - (\ delta \ mathbf {\ theta} \ times \ mathbf {x}) \ cdot \ nabla.}

U(R(\delta \mathbf {\theta }))=1-(\delta \mathbf {\theta } \times \mathbf {x})\cdot \nabla.

После того же возведения в степень как описано выше, мы приходим к оператору вращения в базисе положения, который является экспоненциальной производной по направлению:

U (R (θ)) = exp ⁡ (- (θ × x) ⋅ ∇). {\ displaystyle U (R (\ mathbf {\ theta})) = \ exp (- (\ mathbf {\ theta} \ times \ mathbf {x}) \ cdot \ nabla).}

U(R(\mathbf {\theta }))=\exp(-(\mathbf {\theta } \times \mathbf {x})\cdot \nabla).

Нормальная производная

A производная по нормали - это производная по направлению, взятая в направлении нормали (то есть ортогонально ) к некоторой поверхности в пространстве или, в более общем случае, вдоль поля вектора нормали , ортогонального некоторому гиперповерхность. См., Например, граничное условие Неймана. Если нормальное направление обозначено $n {\ displaystyle \ mathbf {n}}$ $\mathbf {n}$ , то производная по направлению функции f иногда обозначается как $∂ f ∂ n {\ displaystyle { \ frac {\ partial f} {\ partial n}}}$ $\frac{ \partial f}{\partial n}$ . В других обозначениях

∂ f ∂ n = ∇ f (x) ⋅ n = ∇ n f (x) = ∂ f ∂ x ⋅ n = D f (x) [n]. {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {n}}} = \ nabla f (\ mathbf {x}) \ cdot \ mathbf {n} = \ nabla _ {\ mathbf {n}} {f} (\ mathbf {x}) = {\ frac {\ partial f} {\ partial \ mathbf {x}}} \ cdot \ mathbf {n} = Df (\ mathbf {x}) [\ mathbf {n }].}

{\frac {\partial f}{\partial \mathbf {n} }}=\nabla f(\mathbf {x})\cdot \mathbf {n} =\nabla _{\mathbf {n} }{f}(\mathbf {x})={\frac {\partial f}{\partial \mathbf {x} }}\cdot \mathbf {n} =Df(\mathbf {x})[\mathbf {n} ].

В механике сплошной среды твердых тел

Некоторые важные результаты в механике сплошной среды требуют производных векторов по векторам и тензоров по векторам и тензорам. Директива directional обеспечивает систематический способ поиска этих производных.

Ниже приведены определения производных по направлению для различных ситуаций. Предполагается, что функции достаточно гладкие, чтобы можно было брать производные.

Производные скалярных функций векторов

Пусть $f (v) {\ displaystyle f (\ mathbf {v})}$ $f(\mathbf{v})$ является вещественным значная функция вектора $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ . Тогда производная от $f (v) {\ displaystyle f (\ mathbf {v})}$ $f(\mathbf{v})$ по $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ (или в $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ ) в направлении $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ определяется как

∂ е ∂ v ⋅ U знак равно D е (v) [u] = [dd α f (v + α u)] α = 0 {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {v }}} \ cdot \ mathbf {u} = Df (\ mathbf {v}) [\ mathbf {u}] = \ left [{\ frac {d} {d \ alpha}} ~ f (\ mathbf {v} + \ alpha ~ \ mathbf {u}) \ right] _ {\ alpha = 0}}

\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = Df(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~f(\mathbf{v} + \alpha~\mathbf {u})\right]_{\alpha = 0}

для всех векторов $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ .

Свойства:

If $е (v) = f 1 (v) + f 2 (v) {\ displaystyle f (\ mathbf {v}) = f_ {1} (\ mathbf {v}) + f_ {2} (\ mathbf { v})}$ $f(\mathbf{v}) = f_1(\mathbf{v}) + f_2(\mathbf{v})$ , то $∂ f ∂ v ⋅ u = (∂ f 1 ∂ v + ∂ f 2 ∂ v) ⋅ u. {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = \ left ({\ frac {\ partial f_ {1}} {\ partial \ mathbf {v) }}} + {\ frac {\ partial f_ {2}} {\ partial \ mathbf {v}}} \ right) \ cdot \ mathbf {u}.}$ ${\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}+{\frac {\partial f_{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u}.$
Если $f (v) = f 1 (v) е 2 (v) {\ displaystyle f (\ mathbf {v}) = f_ {1} (\ mathbf {v}) ~ f_ {2} (\ mathbf {v})}$ $f(\mathbf{v}) = f_1(\mathbf{v})~ f_2(\mathbf{v})$ тогда $∂ f ∂ v ⋅ u = (∂ f 1 ∂ v ⋅ u) f 2 (v) + f 1 (v) (∂ f 2 ∂ v ⋅ u). {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = \ left ({\ frac {\ partial f_ {1}} {\ partial \ mathbf {v) }}} \ cdot \ mathbf {u} \ right) ~ f_ {2} (\ mathbf {v}) + f_ {1} (\ mathbf {v}) ~ \ left ({\ frac {\ partial f_ {2 }} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} \ right).}$ ${\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v})+f_{1}(\mathbf {v})~\left({\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right).$
Если $f (v) = f 1 (f 2 (v)) {\ displaystyle f ( \ mathbf {v}) = f_ {1} (f_ {2} (\ mathbf {v}))}$ $f(\mathbf{v}) = f_1(f_2(\mathbf{v}))$ , затем $∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ∂ f 2 ∂ v ⋅ u. {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = {\ frac {\ partial f_ {1}} {\ partial f_ {2}}} ~ {\ frac {\ partial f_ {2}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u}.}$ ${\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~{\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u}.$

Производные векторных функций векторов

Пусть $f (v) {\ displaystyle \ mathbf {f} (\ mathbf {v})}$ $\mathbf{f}(\mathbf{v})$ быть векторной функцией вектора $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ . Тогда производная от $f (v) {\ displaystyle \ mathbf {f} (\ mathbf {v})}$ $\mathbf{f}(\mathbf{v})$ по $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ (или в $v {\ displaystyle \ mathbf {v}}$ $\mathbf {v}$ ) в направлении $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ это тензор второго порядка, определенный как

∂ f ∂ v ⋅ u = D f (v) [u] = [dd α f (v + α u)] α = 0 {\ displaystyle {\ frac {\ partial \ mathbf {f}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = D \ mathbf {f} (\ mathbf {v}) [\ mathbf {u}] = \ left [{\ frac {d} {d \ alpha}} ~ \ mathbf {f} (\ mathbf {v} + \ alpha ~ \ mathbf {u}) \ right] _ {\ alpha = 0}}

\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = D\mathbf{f}(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~\mathbf{f}(\mathbf{v} + \alpha~\mathbf{u})\right]_{\alpha = 0}

для всех векторов $u {\ displaystyle \ mathbf {u}}$ $\mathbf {u}$ .

Свойства:

Если $f (v) = f 1 (v) + f 2 (v) {\ displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} (\ mathbf {v}) + \ mathbf {f} _ {2} (\ mathbf {v})}$ $\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v}) + \mathbf{f}_2(\mathbf{v})$ , то $∂ f ∂ v ⋅ u = (∂ f 1 ∂ v + ∂ f 2 ∂ v) ⋅ u. {\ displaystyle {\ frac {\ partial \ mathbf {f}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = \ left ({\ frac {\ partial \ mathbf {f} _ {1 }} {\ partial \ mathbf {v}}} + {\ frac {\ partial \ mathbf {f} _ {2}} {\ partial \ mathbf {v}}} \ right) \ cdot \ mathbf {u}. }$ ${\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}+{\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u}.$
Если $f (v) = f 1 (v) × f 2 (v) {\ displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} ( \ mathbf {v}) \ times \ mathbf {f} _ {2} (\ mathbf {v})}$ $\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v})\times\mathbf{f}_2(\mathbf{v})$ , затем $∂ f ∂ v ⋅ u = (∂ f 1 ∂ v ⋅ u) × f 2 (v) + f 1 (v) × (∂ f 2 ∂ v ⋅ u). {\ displaystyle {\ frac {\ partial \ mathbf {f}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = \ left ({\ frac {\ partial \ mathbf {f} _ {1 }} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} \ right) \ times \ mathbf {f} _ {2} (\ mathbf {v}) + \ mathbf {f} _ {1} (\ mathbf {v}) \ times \ left ({\ frac {\ partial \ mathbf {f} _ {2}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} \ right).}$ ${\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}\cdot \math bf {u} \right)\times \mathbf {f} _{2}(\mathbf {v})+\mathbf {f} _{1}(\mathbf {v})\times \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right).$
Если $f (v) = f 1 (f 2 (v)) {\ displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} (\ mathbf { f} _ {2} (\ mathbf {v}))}$ $\mathbf{f}(\mathbf{v}) = \math bf{f}_1(\mathbf{f}_2(\mathbf{v}))$ , затем $∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ⋅ (∂ f 2 ∂ v ⋅ u). {\ displaystyle {\ frac {\ partial \ mathbf {f}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u} = {\ frac {\ partial \ mathbf {f} _ {1}} { \ partial \ mathbf {f} _ {2}}} \ cdot \ left ({\ frac {\ partial \ mathbf {f} _ {2}} {\ partial \ mathbf {v}}} \ cdot \ mathbf {u } \ right).}$ ${\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {f} _{2}}}\cdot \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right).$

Производные скалярных функций от тензоров второго порядка

Пусть $f (S) {\ displaystyle f (\ mathbf {S})}$ $f(\mathbf {S})$ быть вещественной функцией тензора второго порядка $S {\ displaystyle \ mathbf {S}}$ $\mathbf {S}$ . Тогда производная от $f (S) {\ displaystyle f (\ mathbf {S})}$ $f(\mathbf {S})$ по $S {\ displaystyle \ mathbf {S}}$ $\mathbf {S}$ (или в $S {\ displaystyle \ mathbf {S}}$ $\mathbf {S}$ ) в направлении $T {\ displaystyle \ mathbf {T}}$ $\mathbf {T}$ - это тензор второго порядка определяется как

∂ f ∂ S: T = D f (S) [T] = [dd α f (S + α T)] α = 0 {\ displaystyle {\ frac {\ частичный f} {\ partial \ mathbf {S}}}: \ mathbf {T} = Df (\ mathbf {S}) [\ mathbf {T}] = \ left [{\ frac {d} {d \ alpha} } ~ f (\ mathbf {S} + \ alpha \ mathbf {T}) \ right] _ {\ alpha = 0}}

{\frac {\partial f}{\partial \mathbf {S} }}:\mathbf {T} =Df(\mathbf {S})[\mathbf {T} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {S} +\alpha \mathbf {T})\right]_{\alpha =0}

для всех тензоров второго порядка $T {\ displaystyle \ mathbf {T}}$ $\mathbf {T}$ .

Свойства:

Если $f (S) = f 1 (S) + f 2 (S) {\ displaystyle f (\ mathbf {S}) = f_ {1} (\ mathbf {S}) + f_ {2} (\ mathbf {S})}$ $f(\mathbf {S})=f_{1}(\mathbf {S})+f_{2}(\mathbf {S})$ , затем $∂ f ∂ S: T = (∂ f 1 ∂ S + ∂ f 2 ∂ S): T. {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {S}}}: \ mathbf {T} = \ left ({\ frac {\ partial f_ {1}} {\ partial \ mathbf {S}) }} + {\ frac {\ partial f_ {2}} {\ partial \ mathbf {S}}} \ right): \ mathbf {T}.}$ ${\frac {\partial f}{\partial \mathbf {S} }}:\mathbf {T} =\left({\frac {\partial f_{1}}{\partial \mathbf {S} }}+{\frac {\partial f_{2}}{\partial \mathbf {S} }}\right):\mathbf {T}.$
Если $f (S) = f 1 ( S) f 2 (S) {\ displaystyle f (\ mathbf {S}) = f_ {1} (\ mathbf {S}) ~ f_ {2} (\ mathbf {S})}$ $f(\mathbf {S})=f_{1}(\mathbf {S})~f_{2}(\mathbf {S})$ тогда $∂ f ∂ S: T = (∂ f 1 ∂ S: T) f 2 (S) + f 1 (S) (∂ f 2 ∂ S: T). {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {S}}}: \ mathbf {T} = \ left ({\ frac {\ partial f_ {1}} {\ partial \ mathbf {S}) }}: \ mathbf {T} \ right) ~ f_ {2} (\ mathbf {S}) + f_ {1} (\ mathbf {S}) ~ \ left ({\ frac {\ partial f_ {2}} {\ partial \ mathbf {S}}}: \ mathbf {T} \ right).}$ ${\frac {\partial f}{\partial \mathbf {S} }}:\mathbf {T} =\left({\frac {\partial f_{1}}{\partial \mathbf {S} }}:\mathbf {T} \right)~f_{2}(\mathbf {S})+f_{1}(\mathbf {S})~\left({\frac {\partial f_{2}}{\partial \mathbf {S} }}:\mathbf {T} \right).$
Если $f (S) = f 1 (f 2 (S)) {\ displaystyle f (\ mathbf { S}) = f_ {1} (f_ {2} (\ mathbf {S}))}$ $f(\mathbf {S})=f_{1}(f_{2}(\mathbf {S}))$ , затем $∂ f ∂ S: T = ∂ f 1 ∂ f 2 (∂ f 2 ∂ С: Т). {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {S}}}: \ mathbf {T} = {\ frac {\ partial f_ {1}} {\ partial f_ {2}}} ~ \ left ({\ frac {\ partial f_ {2}} {\ partial \ mathbf {S}}}: \ mathbf {T} \ right).}$ ${\frac {\partial f}{\partial \mathbf {S} }}:\mathbf {T} ={\frac {\partial f_{1}}{\partial f_{2}}}~\left({\frac {\partial f_{2}}{\partial \mathbf {S} }}:\mathbf {T} \right).$

Производные тензорнозначных функций от тензоров второго порядка

Пусть $F (S) {\ displaystyle \ mathbf {F} (\ mathbf {S})}$ $\mathbf {F} (\mathbf {S})$ будет тензорнозначной функцией второго порядка от тензора второго порядка $S {\ Displaystyle \ mathbf {S}}$ $\mathbf {S}$ . Тогда производная от $F (S) {\ displaystyle \ mathbf {F} (\ mathbf {S})}$ $\mathbf {F} (\mathbf {S})$ по $S {\ displaystyle \ mathbf {S}}$ $\mathbf {S}$ (или в $S {\ displaystyle \ mathbf {S}}$ $\mathbf {S}$ ) в направлении $T {\ displaystyle \ mathbf {T}}$ $\mathbf {T}$ - тензор четвертого порядка, определенный как

∂ F ∂ S: T = DF (S) [T] = [dd α F (S + α T)] α = 0 {\ displaystyle {\ frac {\ partial \ mathbf {F}} {\ partial \ mathbf {S}}}: \ mathbf {T} = D \ mathbf {F} (\ mathbf {S}) [\ mathbf {T}] = \ left [{\ frac {d} {d \ alpha}} ~ \ mathbf {F} (\ mathbf {S} + \ alpha \ mathbf {T}) \ right] _ {\ alpha = 0}}

{\frac {\partial \mathbf {F} }{\partial \mathbf {S} }}:\mathbf {T} =D\mathbf {F} (\mathbf {S})[\mathbf {T} ]=\left[{\frac {d}{d\alpha }}~\mathbf {F} (\mathbf {S} +\alpha \mathbf {T})\right]_{\alpha =0}

для всех тензоры второго порядка $T {\ displaystyle \ mathbf {T}}$ $\mathbf {T}$ .

Свойства:

Если $F (S) = F 1 (S) + F 2 (S) {\ displaystyle \ mathbf { F} (\ mathbf {S}) = \ mathbf {F} _ {1} (\ mathbf {S}) + \ mathbf {F} _ {2} (\ mathbf {S})}$ $\mathbf {F} (\mathbf {S})=\mathbf {F} _{1}(\mathbf {S})+\mathbf {F} _{2}(\mathbf {S})$ тогда $∂ F ∂ S: T = (∂ F 1 ∂ S + ∂ F 2 ∂ S): T. {\ displaystyle {\ frac {\ partial \ mathbf {F}} {\ partial \ mathbf {S}}}: \ mathbf {T} = \ left ({\ frac {\ partial \ mathbf {F} _ {1}) } {\ partial \ mathbf {S}}} + {\ frac {\ partial \ mathbf {F} _ {2}} {\ partial \ mathbf {S}}} \ right): \ mathbf {T}.}$ ${\frac {\partial \mathbf {F} }{\partial \mathbf {S} }}:\mathbf {T} =\left({\frac {\partial \mathbf {F} _{1}}{\partial \mathbf {S} }}+{\frac {\partial \mathbf {F} _{2}}{\partial \mathbf {S} }}\right):\mathbf {T}.$
Если $F (S) = F 1 (S) ⋅ F 2 (S) {\ displaystyle \ mathbf {F} (\ mathbf {S}) = \ mathbf {F} _ {1} (\ mathbf {S}) \ cdot \ mathbf {F} _ {2} (\ mathbf {S})}$ $\mathbf {F} (\mathbf {S})=\mathbf {F} _{1}(\mathbf {S})\cdot \mathbf {F} _{2}(\mathbf {S})$ , затем $∂ F ∂ S: T = (∂ F 1 ∂ S: T) ⋅ F 2 (S) + F 1 (S) ⋅ (∂ F 2 ∂ S: T). {\ displaystyle {\ frac {\ partial \ mathbf {F}} {\ partial \ mathbf {S}}}: \ mathbf {T} = \ left ({\ frac {\ partial \ mathbf {F} _ {1}) } {\ partial \ mathbf {S}}}: \ mathbf {T} \ right) \ cdot \ mathbf {F} _ {2} (\ mathbf {S}) + \ mathbf {F} _ {1} (\ mathbf {S}) \ cdot \ left ({\ frac {\ partial \ mathbf {F} _ {2}} {\ partial \ mathbf {S}}}: \ mathbf {T} \ right).}$ ${\frac {\partial \mathbf {F} }{\partial \mathbf {S} }}:\mathbf {T} =\left({\frac {\partial \mathbf {F} _{1}}{\partial \mathbf {S} }}:\mathbf {T} \right)\cdot \mathbf {F} _{2}(\mathbf {S})+\mathbf {F} _{1}(\mathbf {S})\cdot \left({\frac {\partial \mathbf {F} _{2}}{\partial \mathbf {S} }}:\mathbf {T} \right).$
Если $F (S) = F 1 (F 2 (S)) {\ displaystyle \ mathbf {F} (\ mathbf {S}) = \ mathbf {F} _ {1} (\ mathbf {F} _ {2} (\ mathbf {S}))}$ $\mathbf {F} (\mathbf {S})=\mathbf {F} _{1}(\mathbf {F} _{2}(\mathbf {S}))$ , затем $∂ F ∂ S: T = ∂ F 1 ∂ F 2: (∂ F 2 ∂ S: T). {\ displaystyle {\ frac {\ partial \ mathbf {F}} {\ partial \ mathbf {S}}}: \ mathbf {T} = {\ frac {\ partial \ mathbf {F} _ {1}} {\ partial \ mathbf {F} _ {2}}}: \ left ({\ frac {\ partial \ mathbf {F} _ {2}} {\ partial \ mathbf {S}}}: \ mathbf {T} \ right).}$ ${\frac {\partial \mathbf {F} }{\partial \mathbf {S} }}:\mathbf {T} ={\frac {\partial \mathbf {F} _{1}}{\partial \mathbf {F} _{2}}}:\left({\frac {\partial \mathbf {F} _{2}}{\partial \mathbf {S} }}:\mathbf {T} \right).$
Если $f (S) = f 1 (F 2 (S)) {\ displaystyle f (\ mathbf {S}) = f_ {1} (\ mathbf {F} _ {2} (\ mathbf {S}))}$ $f(\mathbf {S})=f_{1}(\mathbf {F} _{2}(\mathbf {S}))$ , затем $∂ f ∂ S: T = ∂ f 1 ∂ F 2: (∂ F 2 ∂ S: T). {\ displaystyle {\ frac {\ partial f} {\ partial \ mathbf {S}}}: \ mathbf {T} = {\ frac {\ partial f_ {1}} {\ partial \ mathbf {F} _ {2 }}}: \ left ({\ frac {\ partial \ mathbf {F} _ {2}} {\ partial \ mathbf {S}}}: \ mathbf {T} \ right).}$ ${\frac {\partial f}{\partial \mathbf {S} }}:\mathbf {T} ={\frac {\partial f_{1}}{\partial \mathbf {F} _{2}}}:\left({\frac {\partial \mathbf {F} _{2}}{\partial \mathbf {S} }}:\mathbf {T} \right).$

См. также

Notes

References

Hildebrand, FB (1976). Advanced Calculus for Applications. Прентис Холл. ISBN 0-13-011189-9.
K.F. Riley; М.П. Hobson; С.Дж. Bence (2010). Mathematical methods for physics and engineering. Издательство Кембриджского университета. ISBN 978-0-521-86153-3.
Shapiro, A. (1990). "On concepts of directional differentiability". Журнал теории оптимизации и приложений. 66(3): 477–487. doi :10.1007/BF00940933.

External links