Групповое представление

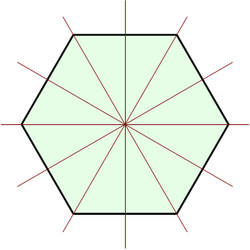
Групповой гомоморфизм в общую линейную группу в векторном пространстве Представление группы "действует "на объекте. Простым примером является то, как симметрии правильного многоугольника, состоящего из отражений и поворотов, преобразуют многоугольник.

В поле Mathematical в теории представлений, представления групп описывают абстрактные группы в терминах биективных линейных преобразований (т. Е. автоморфизмов ) векторные пространства ; в частности, они могут использоваться для представления групповых элементов как обратимых матриц, так что групповая операция может быть представлена ​​с помощью умножения матриц. Представления групп важны, потому что они позволяют многие теоретико-групповые проблемы сводить к проблемам в линейной алгебре, что хорошо понятно. Они также важны в физике, потому что, например, они описывают, как группа симметрии физической системы влияет на решения уравнений, описывающих эту систему.

Термин «представление группы» также используется в более общем смысле для обозначения любого «описания» группы как группы преобразований некоторого математического объекта. Более формально «представление» означает гомоморфизм из группы в группу автоморфизмов объекта. Если объект является векторным пространством, у нас есть линейное представление. Некоторые люди используют реализацию для общего понятия и резервируют термин представление для частного случая линейных представлений. Основная часть статьи посвящена теории линейных представлений; см. последний раздел для обобщений.

Содержание

• 1 Разделы теории представлений групп
• 2 Определения
• 3 Примеры
• 4 Сводимость
• 5 Обобщения
  • 5.1 Теоретико-множественные представления
  • 5.2 Представления в других категориях
• 6 См. Также
• 7 Ссылки

Разделы теории представлений групп

Теория представлений групп делится на подтеории в зависимости от вида представляемой группы. Различные теории сильно различаются в деталях, хотя некоторые основные определения и концепции схожи. Наиболее важные разделы:

• Конечные группы - Представления групп являются очень важным инструментом в изучении конечных групп. Они также возникают в приложениях теории конечных групп к кристаллографии и геометрии. Если поле скаляров векторного пространства имеет характеристику p, и если p делит порядок группы, то это называется теорией модульного представления ; этот частный случай имеет очень разные свойства. См. Теория представлений конечных групп.
• Компактные группы или локально компактные группы - Многие результаты теории конечных представлений групп доказываются усреднением по группе. Эти доказательства могут быть перенесены на бесконечные группы путем замены среднего на интеграл при условии, что можно определить приемлемое понятие интеграла. Это можно сделать для локально компактных групп, используя меру Хаара. Полученная в результате теория является центральной частью гармонического анализа. Двойственность Понтрягина описывает теорию коммутативных групп как обобщенное преобразование Фурье. См. Также: Теорема Питера – Вейля.
• Группы Ли - Многие важные группы Ли компактны, поэтому к ним применимы результаты теории компактных представлений. Также используются другие техники, специфичные для групп Ли. Большинство групп, важных в физике и химии, являются группами Ли, и их теория представлений имеет решающее значение для применения теории групп в этих областях. См. Представления групп Ли и Представления алгебр Ли.
• Линейные алгебраические группы (или, в более общем смысле, аффинные групповые схемы ) - это аналоги групп Ли, но в более общих полях, чем просто R или C . Хотя линейные алгебраические группы имеют классификацию, очень похожую на классификацию групп Ли, и дают начало тем же семействам алгебр Ли, их представления довольно разные (и гораздо менее понятны). Аналитические методы, используемые для изучения групп Ли, должны быть заменены методами из алгебраической геометрии, где относительно слабая топология Зарисского вызывает множество технических сложностей.
• Некомпактная топология группы - класс некомпактных групп слишком широк для построения какой-либо общей теории представлений, но были изучены конкретные частные случаи, иногда с использованием специальных методов. Полупростые группы Ли имеют глубокую теорию, основанную на компактном случае. Дополнительные разрешимые группы Ли нельзя классифицировать таким же образом. Общая теория групп Ли имеет дело с полупрямыми произведениями двух типов с помощью общих результатов, называемых теорией Макки, которые являются обобщением методов классификации Вигнера..

Теория представлений также сильно зависит от типа векторного пространства, на котором действует группа. Различают конечномерные представления и бесконечномерные. В бесконечномерном случае важны дополнительные структуры (например, является ли пространство гильбертовым пространством, банаховым пространством и т. Д.).

Также необходимо учитывать тип поля , над которым определяется векторное пространство. Самый важный случай - это поле комплексных чисел. Другими важными случаями являются поле действительных чисел, конечных полей и поля p-адических чисел. В общем, с алгебраически замкнутыми полями легче работать, чем с неалгебраически замкнутыми. характеристика поля также имеет значение; многие теоремы для конечных групп зависят от характеристики поля, не делящего порядок группы.

Определения

A представление группы G в векторном пространстве V над полем K является гомоморфизмом группы из G в GL (V), общей линейной группой на V. То есть представлением представляет собой карту

$\rho :\; G\; \to \; GL\; (V)\; \{\backslash \; displaystyle\; \backslash \; rho\; \backslash \; двоеточие\; G\; \backslash \; to\; \backslash \; mathrm\; \{GL\}\; (V)\}$

такое, что

$\rho \; (g\; 1\; g\; 2)\; =\; \rho \; (g\; 1)\; \rho \; (g\; 2)\; для\; всех\; g\; 1,\; g\; 2\; \in \; G.\; \{\backslash \; displaystyle\; \backslash \; rho\; (g\_\; \{1\}\; g\_\; \{2\})\; =\; \backslash \; rho\; (g\_\; \{1\})\; \backslash \; rho\; (g\_\; \{2\}),\; \backslash \; qquad\; \{\backslash \; text\; \{для\; всех\}\}\; g\_\; \{1\},\; g\_\; \{\; 2\}\; \backslash \; in\; G.\}$

Здесь V называется пространством представления, а размерность V называется измерением представления. Обычно V сам по себе является представлением, когда гомоморфизм ясен из контекста.

В случае, когда V имеет конечную размерность n, обычно выбирают базис для V и идентифицируют GL (V) с GL (n, K), группой n- by-n обратимые матрицы в поле K.

• Если G - топологическая группа, а V - топологическое векторное пространство, непрерывное представление группы G на V есть представление ρ такое, что приложение Φ: G × V → V, определенное формулой Φ (g, v) = ρ (g) (v), является непрерывным.
• ядром представление ρ группы G определяется как нормальная подгруппа группы G, образ которой при ρ является тождественным преобразованием:

$ker\; \; \rho \; =\; \{g\; \in \; G\; \mid \; \rho \; (g)\; =\; id\}.\; \{\backslash \; displaystyle\; \backslash \; ker\; \backslash \; rho\; =\; \backslash \; left\; \backslash \; \{g\; \backslash \; in\; G\; \backslash \; mid\; \backslash \; rho\; (g)\; =\; \backslash \; mathrm\; \{id\}\; \backslash \; right\; \backslash \}.\}$

A точное представление - это то, в котором гомоморфизм G → GL (V) является инъективным ; другими словами, та, ядро ​​которой является тривиальной подгруппой {e}, состоящей только из единичного элемента группы.

• Для двух K векторных пространств V и W, два представления ρ: G → GL (V) и π: G → GL (W) называются эквивалентными или изоморфными, если существует изоморфизм векторных пространств α: V → W, так что для всех g в G

$\alpha \; \circ \; \rho \; (g)\; \circ \; \alpha \; -\; 1\; =\; \pi \; (g).\; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; circ\; \backslash \; rho\; (g)\; \backslash \; circ\; \backslash \; alpha\; ^\; \{-\; 1\}\; =\; \backslash \; pi\; (g).\}$

Примеры

Рассмотрим комплексное число u = e, которое имеет свойство u = 1. Циклическая группа C3= {1, u, u} имеет представление ρ на C, задаваемое формулой

$\rho \; (1)\; =\; [1\; 0\; 0\; 1]\; \rho \; (u)\; =\; [1\; 0\; 0\; u]\; \rho \; (u\; 2)\; =\; [1\; 0\; 0\; u\; 2].\; \{\backslash \; Displaystyle\; \backslash \; rho\; \backslash \; left\; (1\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; rho\; \backslash \; left\; (u\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; u\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; rho\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; u\; ^\; \{2\}\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}.\; \}$

Это представление является точным, поскольку ρ является взаимно однозначным отображением.

Другое представление для C 3 на C, изоморфное предыдущему, - это σ, задаваемое формулой:

$\sigma \; (1)\; =\; [1\; 0\; 0\; 1]\; \sigma \; (u)\; =\; [u\; 0\; 0\; 1]\; \sigma \; (u\; 2)\; =\; [u\; 2\; 0\; 0\; 1].\; \{\backslash \; Displaystyle\; \backslash \; sigma\; \backslash \; left\; (1\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; sigma\; \backslash \; left\; (u\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; u\; 0\; \backslash \backslash \; 0\; 1\; \backslash \backslash \backslash \; конец\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; sigma\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; u\; ^\; \{2\}\; 0\; \backslash \backslash \; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}.\}$

Группа C 3 также может быть точно представлена ​​на R с помощью τ, задаваемого следующим образом:

$\tau \; (1)\; =\; [1\; 0\; 0\; 1]\; \tau \; (u)\; =\; [a\; -\; bba]\; \tau \; (u\; 2)\; =\; [ab\; -\; ba]\; \{\backslash \; displaystyle\; \backslash \; tau\; \backslash \; left\; (1\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; \backslash \backslash \; 0\; 1\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; tau\; \backslash \; left\; (u\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; a\; -b\; \backslash \backslash \; b\; a\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\; \backslash \; qquad\; \backslash \; tau\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; right)\; =\; \{\backslash \; begin\; \{bmatrix\}\; a\; b\; \backslash \backslash \; -\; b\; a\; \backslash \backslash \backslash \; end\; \{bmatrix\}\}\}$

где

$a\; =\; Re\; (u)\; =\; -\; 1\; 2,\; b\; =\; Im\; (u)\; =\; 3\; 2.\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; text\; \{Re\}\}\; (u)\; =\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\},\; \backslash \; qquad\; b\; =\; \{\backslash \; text\; \{Im\}\}\; (u)\; =\; \{\backslash \; tfrac\; \{\backslash \; sqrt\; \{\; 3\}\}\; \{2\}\}.\}$

Сводимость

Подпространство W в V, которое инвариантно относительно действия группы, называется подпредставлением. Если V имеет ровно два подпредставления, а именно нульмерное подпространство и само V, то представление называется неприводимым ; если у него есть собственное подпредставление ненулевой размерности, это представление называется приводимым . Представление нулевой размерности не считается ни сводимым, ни неприводимым, так же как число 1 не считается ни составным, ни простым.

При условии, что характеристика поля K не делит размер группы, представления конечных групп могут быть разложены на прямую сумму неприводимых подпредставлений (см. теорему Машке ). Это, в частности, справедливо для любого представления конечной группы над комплексными числами, поскольку характеристика комплексных чисел равна нулю, что никогда не делит размер группы.

В приведенном выше примере первые два заданных представления (ρ и σ) разложимы на два одномерных подпредставления (заданных span {(1,0)} и span {(0,1)}), а третье представление (τ) неприводимо.

Обобщения

Теоретико-множественные представления

Теоретико-множественное представление (также известное как групповое действие или представление перестановки) группы G на набор X задается функцией ρ: G → X, набором функций от X до X, так что для всех g 1, g 2 в G и все x в X:

$\rho \; (1)\; [x]\; =\; x\; \{\backslash \; displaystyle\; \backslash \; rho\; (1)\; [x]\; =\; x\}$

$\rho \; (г\; 1\; г\; 2)\; [Икс]\; знак\; равно\; \rho \; (г\; 1)\; [\rho \; (г\; 2)\; [х]],\; \{\backslash \; Displaystyle\; \backslash \; rho\; (g\_\; \{1\}\; g\_\; \{2\})\; [x]\; =\; \backslash \; rho\; (g\_\; \{\; 1\})\; [\backslash \; rho\; (g\_\; \{2\})\; [x]],\}$

где $1\; \{\backslash \; displaystyle\; 1\}$- тождественный элемент G. Это условие и аксиомы для группа подразумевает, что ρ (g) является биекцией (или перестановкой ) для всех g в G. Таким образом, мы можем эквивалентно определить представление перестановки как гомоморфизм группы от G к симметричной группе SXX.

Для получения дополнительной информации по этой теме см. Статью о групповом действии.

Представления в других категориях

Каждую группу G можно рассматривать как категорию с одним объектом; морфизмы в этой категории - это просто элементы G. Для произвольной категории C представление G в C является функтором из G в C. Такой функтор выбирает объект X в C и гомоморфизм группы из G в Aut (X), группа автоморфизмов из X.

В случае, когда C равно Vect K, категория векторных пространств над полем K, это определение эквивалентно линейному представлению. Аналогично, теоретико-множественное представление - это просто представление G в категории множеств.

. Когда C равно Ab, категории абелевых групп, полученные объекты называются G-модулями.

В качестве другого примера рассмотрим категорию топологических пространств, Top . Представления в Top - это гомоморфизмы из G в группу гомеоморфизмов топологического пространства X.

Два типа представлений, тесно связанных с линейными представлениями:

• проективные представления : в категории проективных пространств. Их можно описать как «линейные представления до скалярных преобразований».
• аффинные представления : в категории аффинных пространств. Например, евклидова группа действует аффинно в евклидовом пространстве.

См. Также

• Неприводимые представления
• Таблица символов
• Теория символов
• Молекулярная симметрия
• Список Темы гармонического анализа
• Список тем теории представлений
• Теория представлений конечных групп
• Полупростое представление

Литература

• Уильям Фултон ; Харрис, Джо (1991). Теория представлений. Первый курс. Тексты для выпускников по математике, Чтения по математике. 129 . Нью-Йорк: Springer-Verlag. DOI : 10.1007 / 978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.. Введение в теорию представлений с акцентом на группы Ли.
• Юрий Иванович Любич. Введение в теорию банаховых представлений групп. Перевод с русскоязычного издания 1985 г. (Харьков, Украина). Birkhäuser Verlag. 1988.