Группа кос

редактировать

Обычная коса на пяти прядях. Каждая стрелка составляет два дополнительных элемента

B 5 {\ displaystyle B_ {5}}

B_{5}

В математике группа кос на n прядях (обозначена $B n {\ displaystyle B_ {n}}$ $B_{n}$ ), также известная как группа кос Артина, - это группа, элементы которой являются классами эквивалентности n-кос ( например, под окружающей изотопией ), и чья групповая операция представляет собой композицию кос (см. § Введение). Примеры применения групп кос включают теорию узлов, где любой узел может быть представлен как замыкание определенных кос (результат, известный как теорема Александера ); в математической физике, где каноническое представление группы кос в Артине соответствует уравнению Янга – Бакстера (см. § Основные свойства) ; и в монодромии инварианты алгебраической геометрии.

Содержание

1 Введение
2 Приложения
3 Формальная обработка
- 3.1 Закрытые косы
- 3.2 Индекс косы
4 История
5 Основные свойства
- 5.1 Генераторы и отношения
- 5.2 Дополнительные свойства
6 Взаимодействия
- 6.1 Связь с симметричной группой и чистой группой кос
- 6.2 Связь между $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ и модульная группа
- 6.3 Связь с группой классов отображения и классификация кос
- 6.4 Связь с теорией узлов
- 6.5 Вычислительные аспекты
7 Действия
- 7.1 Представления
8 Бесконечно генерируемые группы кос
9 Когомология
10 См. Также
11 Ссылки
12 Дополнительная литература
13 Внешние ссылки

Введение

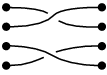
Во введении пусть n = 4; обобщение на другие значения n будет простым. Рассмотрим два набора из четырех предметов, лежащих на столе, причем предметы в каждом наборе расположены вертикальной линией и так, что один набор находится рядом с другим. (На рисунках ниже это черные точки.) Используя четыре нити, каждый элемент первого набора соединяется с элементом второго набора, так что получается взаимно однозначное соответствие. Такое соединение называется косой. Часто одни пряди должны проходить над другими или под другими, и это очень важно: следующие два соединения - это разные косы:

отличается от

С другой стороны, два таких соединения, которые могут выглядеть одинаково при «вытягивании прядей» считается одна и та же коса:

то же самое, что и

Все пряди требуется перемещать слева направо; такие узлы, как следующие, не считаются косами:

не коса

Любые две косы можно составить, нарисовав первую рядом со второй, указав четыре элемента в середине и соединив соответствующие пряди:

составленный из

дает

Другой пример:

составлен из

дает

Состав косичек σ и τ записывается как στ.

Набор всех кос на четырех прядях обозначается $B 4 {\ displaystyle B_ {4}}$ $B_{4}$ . Вышеупомянутая композиция косичек действительно является операцией group. Идентификационный элемент - это коса, состоящая из четырех параллельных горизонтальных прядей, а обратная коса состоит из той косы, которая «развязывает» все, что сделала первая коса, что получается путем переворачивания. диаграмму, подобную приведенной выше, через вертикальную линию, проходящую через его центр. (Первые два примера косы выше противоположны друг другу.)

Приложения

Теория кос недавно была применена к механике жидкости, особенно к области хаотическое перемешивание в потоках жидкости. Сплетение (2 + 1) -мерных пространственно-временных траекторий, образованных движением физических стержней, периодических орбит или «призрачных стержней», и почти инвариантных множеств было использовано для оценки топологической энтропии нескольких спроектированные и встречающиеся в природе жидкостные системы с использованием классификации Нильсена – Терстона.

Другая область интенсивных исследований, включающая группы кос и связанные топологические концепции в контексте квантовой физики, находится в теории и (предполагаемая) экспериментальная реализация так называемого аньонов. Они вполне могут стать основой для квантовых вычислений с исправлением ошибок, и поэтому их абстрактное исследование в настоящее время имеет фундаментальное значение в квантовой информации.

Формальная обработка

Чтобы выразить выше неформального обсуждения групп кос на твердой основе, необходимо использовать гомотопическую концепцию алгебраической топологии, определяя группы кос как фундаментальные группы из конфигурационное пространство. В качестве альтернативы, можно определить группу кос чисто алгебраически через отношения кос, имея в виду изображения только для руководства интуицией.

Чтобы объяснить, как свести группу кос в смысле Артина к фундаментальной группе, мы рассматриваем связное многообразие $X {\ displaystyle X}$ $X$ размером не менее 2. симметричное произведение из $n {\ displaystyle n}$ $n$ копий $X {\ displaystyle X}$ $X$ означает частное от $X n {\ displaystyle X ^ {n}}$ $X^{n}$ , $n {\ displaystyle n}$ $n$ -fold декартово произведение $X {\ displaystyle X}$ $X$ действием перестановки симметричной группы на $n {\ displaystyle n}$ $n$ цепях, работающих с индексами координат. То есть упорядоченная кортеж $n {\ displaystyle n}$ $n$ находится на той же орбите, что и любой другой, который представляет собой переупорядоченную его версию.

Путь в $n {\ displaystyle n}$ $n$ -сложном симметричном произведении - это абстрактный способ обсуждения $n {\ displaystyle n}$ $n$ точки $X {\ displaystyle X}$ $X$ , рассматриваемые как неупорядоченный $n {\ displaystyle n}$ $n$ -кортеж, независимо отслеживая $n {\ displaystyle n}$ $n$ строк. Поскольку мы должны требовать, чтобы строки никогда не проходили друг через друга, необходимо перейти в подпространство $Y {\ displaystyle Y}$ $Y$ симметричного произведения орбит $n { \ displaystyle n}$ $n$ - наборы различных точек. То есть мы удаляем все подпространства $X n {\ displaystyle X ^ {n}}$ $X^{n}$ , определенные условиями $xi = xj {\ displaystyle x_ {i} = x_ {j} }$ $x_{i}=x_{j}$ для всех $1 ≤ i < j ≤ n {\displaystyle 1\leq i$ $1\leq i<j\leq n$ . Это инвариантно относительно симметричной группы, и $Y {\ displaystyle Y}$ $Y$ является частным по симметричной группе неисключенных $n {\ displaystyle n}$ $n$ - пары. При выполнении условия измерения $Y {\ displaystyle Y}$ $Y$ будет подключено.

Таким образом, используя это определение, мы можем вызвать группу кос $X {\ displaystyle X}$ $X$ с $n {\ displaystyle n}$ $n$ строки фундаментальная группа $Y {\ displaystyle Y}$ $Y$ (для любого выбора базовой точки - это четко определенный от до изоморфизм). Случай, когда $X {\ displaystyle X}$ $X$ - это евклидова плоскость, является исходной плоскостью Артина. В некоторых случаях можно показать, что более высокие гомотопические группы из $Y {\ displaystyle Y}$ $Y$ тривиальны.

Закрытые плетения

Когда X представляет собой плоскость, плетение может быть замкнуто, т. Е. Соответствующие концы могут быть соединены попарно, чтобы образовать звено, т. Е. возможно переплетенное объединение возможно связанных петель в трех измерениях. Количество компонентов ссылки может быть любым от 1 до n, в зависимости от перестановки цепей, определяемой ссылкой. Теорема Дж. У. Александер демонстрирует, что каждая ссылка может быть получена таким образом как «замыкание» косы. Сравните с звеньями цепочки.

Разные плетения могут дать одно и то же звено, так же как разные схемы пересечения могут дать начало одному и тому же узлу . В 1935 г. Андрей Марков-младший описал два хода на диаграммах кос, которые дают эквивалентность в соответствующих замкнутых косах. Одноходовая версия теоремы Маркова была опубликована в 1997 году.

Воан Джонс первоначально определил свой многочлен как инвариант косы, а затем показал, что он зависит только от класса замкнутых тесьма.

Теорема Маркова дает необходимые и достаточные условия, при которых замыкания двух кос являются эквивалентными связями.

Индекс кос

«Индекс кос» - наименьшее количество строк, необходимых для создания представления ссылки в виде замкнутой косы. Он равен наименьшему числу кругов Зейферта в любой проекции узла.

История

Группы кос были явно введены Эмилем Артином в 1925 г., хотя (как указал Вильгельм Магнус в 1974 г.) они уже присутствовали в работе Адольфа Гурвица о монодромии 1891 года.

Группы кос могут быть описаны с помощью явного представления, как было показано Эмилем Артином в 1947 году. Группы кос также понимаются более глубокой математической интерпретацией: как фундаментальная группа некоторых конфигурационных пространств.

Как говорит Магнус, Гурвиц дал интерпретацию группы кос как фундаментальную группу конфигурационного пространства (см. теория кос ), интерпретацию, которая была исчез из поля зрения, пока не был вновь открыт Ральфом Фоксом и Ли Нойвиртом в 1962 году.

Основные свойства

Генераторы и отношения

Рассмотрим следующие три косы :


$σ 1 {\ displaystyle \ sigma _ {1}}$ $\sigma _{1}$	$σ 2 {\ displaystyle \ sigma _ {2}}$ $\sigma _{2}$	$σ 3 {\ displaystyle \ sigma _ {3}}$ $\sigma_3$

Каждая коса в $B 4 {\ displaystyle B_ {4}}$ $B_{4}$ можно записать как композицию из нескольких этих кос и их перевернутых. Другими словами, эти три косы образуют группу $B 4 {\ displaystyle B_ {4}}$ $B_{4}$ . Чтобы увидеть это, произвольная коса просматривается слева направо на предмет пересечений; начиная сверху, всякий раз, когда встречается пересечение нитей $i {\ displaystyle i}$ $i$ и $i + 1 {\ displaystyle i + 1}$ $i+1$ , $записывается σ я {\ displaystyle \ sigma _ {i}}$ $\sigma _{i}$ или $σ i - 1 {\ displaystyle \ sigma _ {i} ^ {- 1}}$ $\sigma _{i}^{-1}$ вниз, в зависимости от того, перемещается ли цепочка $i {\ displaystyle i}$ $i$ под или над цепью $i + 1 {\ displaystyle i + 1}$ $i+1$ . Достигнув правого конца, коса была записана как произведение $σ {\ displaystyle \ sigma}$ $\sigma$ и их обратных сторон.

Очевидно, что

(i)

σ 1 σ 3 = σ 3 σ 1 {\ displaystyle \ sigma _ {1} \ sigma _ {3} = \ sigma _ {3} \ sigma _ {1}}

\sigma _{1}\sigma _{3}=\sigma _{3}\sigma _{1}

, хотя следующие два отношения не так очевидны:

(iia)

σ 1 σ 2 σ 1 = σ 2 σ 1 σ 2 {\ displaystyle \ sigma _ { 1} \ sigma _ {2} \ sigma _ {1} = \ sigma _ {2} \ sigma _ {1} \ sigma _ {2}}

\sigma _{1}\sigma _{2}\sigma _{1}=\sigma _{2}\sigma _{1}\sigma _{2}

(iib)

σ 2 σ 3 σ 2 = σ 3 σ 2 σ 3 {\ Displaystyle \ sigma _ {2} \ sigma _ {3} \ sigma _ {2} = \ sigma _ {3} \ sigma _ {2} \ sigma _ {3}}

\sigma _{2}\sigma _{3}\sigma _{2}=\sigma _{3}\sigma _{2}\sigma _{3}

(эти отношения лучше всего можно оценить, нарисовав косу на листе бумаги). Можно показать, что все остальные отношения между косами $σ 1 {\ displaystyle \ sigma _ {1}}$ $\sigma _{1}$ , $σ 2 {\ displaystyle \ sigma _ {2}}$ $\sigma _{2}$ и $σ 3 {\ displaystyle \ sigma _ {3}}$ $\sigma_3$ уже следует из этих соотношений и групповых аксиом.

Обобщая этот пример на $n {\ displaystyle n}$ $n$ нитей, группа $B n {\ displaystyle B_ {n}}$ $B_{n}$ может быть абстрактно определяется через следующее представление :

B n = ⟨σ 1,…, σ n - 1 ∣ σ i σ i + 1 σ i = σ i + 1 σ i σ i + 1, σ i σ j знак равно σ J σ я⟩, {\ Displaystyle B_ {n} = \ left \ langle \ sigma _ {1}, \ ldots, \ sigma _ {n-1} \ mid \ sigma _ {i} \ sigma _ {я +1} \ sigma _ {i} = \ sigma _ {i + 1} \ sigma _ {i} \ sigma _ {i + 1}, \ sigma _ {i} \ sigma _ {j} = \ sigma _ { j} \ sigma _ {i} \ right \ rangle,}

B_{n}=\left\langle \sigma _{1},\ldots,\sigma _{n-1}\mid \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\right\rangle,

где в первой группе отношений $1 ≤ i ≤ n - 2 {\ displaystyle 1 \ leq i \ leq n-2}$ $1\leq i\leq n-2$ и во второй группе отношений, $i - j ≥ 2 {\ displaystyle ij \ geq 2}$ $i-j\geq 2$ . Это представление приводит к обобщению групп кос, называемых группами Артина. Кубические отношения, известные как отношения кос, играют важную роль в теории уравнений Янга – Бакстера.

Дополнительные свойства

Группа кос $B 1 {\ displaystyle B_ {1}}$ $B_{1}$ - тривиальная, $B 2 {\ displaystyle B_ {2}}$ $B_{2}$ - бесконечная циклическая группа $Z {\ displaystyle \ mathbb {Z}}$ $\mathbb {Z}$ и $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ изоморфен группе узлов узла-трилистника - в частности, это бесконечная неабелева группа.
Группа кос из n-прядей $B n {\ displaystyle B_ {n}}$ $B_{n}$ встраивается как подгруппа в группу $(n + 1) {\ displaystyle (n + 1)}$ $(n+1)$ прядей $B n + 1 {\ displaystyle B_ {n + 1}}$ $B_{n+1}$ путем добавления дополнительной нити, которая не пересекает ни одну из первых n нитей. Увеличивающееся объединение групп кос со всеми $n ≥ 1 {\ displaystyle n \ geq 1}$ $n\geq 1$ - это бесконечная группа кос $B ∞ {\ displaystyle B_ { \ infty}}$ $B_{\infty}$ .
Все неидентификационные элементы $B n {\ displaystyle B_ {n}}$ $B_{n}$ имеют бесконечный порядок ; т.е. $B n {\ displaystyle B_ {n}}$ $B_{n}$ без кручения.
На $n {\ displaystyle B_ {n}}$ $B_{n}$ называется порядок Дехорного.
для $n ≥ 3 {\ displaystyle n \ geq 3}$ $n\geq 3$ , $B n {\ displaystyle B_ { n}}$ $B_{n}$ содержит подгруппу, изоморфную свободной группе на двух образующих.
Имеется гомоморфизм $B n → Z {\ displaystyle B_ {n} \ to \ mathbb {Z}}$ $B_{n}\to \mathbb {Z}$ определяется как σ i ↦ 1. Так, например, коса σ 2σ3σ1σ2σ3отображается в 1 + 1 - 1 + 1 + 1 = 3. Это отображение соответствует абелианизации группы кос. Поскольку σ i ↦ k, тогда σ i является тождеством тогда и только тогда, когда $k = 0 {\ displaystyle k = 0}$ $k=0$ . Это доказывает, что генераторы имеют бесконечный порядок.

Взаимодействия

Связь с симметричной группой и чистой группой кос

Забывая, как скручиваются и перекрещиваются пряди, каждая коса на n прядях определяет перестановка на n элементах. Это присвоение связано с композицией и совместимо с ней, и поэтому становится субъективным групповым гомоморфизмом Bn→ S n из группы кос на симметричную группу . Образ косы σ i ∈ B n - это транспозиция s i = (i, i + 1) ∈ S n. Эти транспозиции порождают симметрическую группу, удовлетворяют отношениям группы кос и имеют порядок 2. Это преобразует представление Артина группы кос в представление Кокстера симметрической группы:

S n = ⟨s 1,…, sn - 1 | s i s i + 1 s i = s i + 1 s i s i + 1, s i s j = s j s i для | i - j | ≥ 2, s i 2 = 1⟩. {\ Displaystyle S_ {n} = \ left \ langle s_ {1}, \ ldots, s_ {n-1} | s_ {i} s_ {i + 1} s_ {i} = s_ {i + 1} s_ { i} s_ {i + 1}, s_ {i} s_ {j} = s_ {j} s_ {i} {\ text {for}} | ij | \ geq 2, s_ {i} ^ {2} = 1 \ right \ rangle.}

S_n = \left \langle s_1,\ldots,s_{n-1}| s_i s_{i+1} s_i=s_{i+1} s_i s_{i+1}, s_i s_j = s_j s_i \text{ for } |i-j|\geq 2, s_i^2=1 \right\rangle.

ядро гомоморфизма B n → S n - это подгруппа B n, называемая группа чистой плетеной косы на n прядях, обозначенная как P n. В чистой косе начало и конец каждой пряди находятся в одном положении. Группы чистых кос укладываются в короткую точную последовательность

1 → F n - 1 → P n → P n - 1 → 1. {\ displaystyle 1 \ to F_ {n-1} \ to P_ {n} \ to P_ {n-1} \ to 1.}

1\to F_{n-1} \to P_n \to P_{n-1}\to 1.

Эта последовательность разбивает, и поэтому чистые группы кос реализуются как повторяющиеся полупрямые произведения свободных групп.

Связь между $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ и модульной группой

B 3 {\ displaystyle B_ {3}}

B_{3}

является универсальным центральным расширением модульной группы.

Группа кос $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ является универсальным центральным расширением из модульной группы $PSL (2, Z) {\ displaystyle \ mathrm {PSL} (2, \ mathbb {Z})}$ $\mathrm {PSL} (2,\mathbb {Z})$ , при этом они сидят как решетки внутри (топологической) универсальной накрывающей группы

SL (2, R) ¯ → PSL (2, R) {\ displaystyle {\ overline {\ mathrm {SL} (2, \ mathbb {R})}} \ to \ mathrm {PSL} (2, \ mathbb {R})}

{\overline {\mathrm {SL} (2,\mathbb {R})}}\to \mathrm {PSL} (2,\mathbb {R})

Кроме того, модульная группа имеет тривиальный центр, и, следовательно, модульная группа изоморфна фактор-группе из $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ по модулю центра, $Z (B 3), {\ displaystyle Z (B_ {3}),}$ $Z(B_{3}),$ и, эквивалентно, группе внутренних автоморфизмов из $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ .

Вот конструкция o е это изоморфизм. Определите

a = σ 1 σ 2 σ 1, b = σ 1 σ 2 {\ displaystyle a = \ sigma _ {1} \ sigma _ {2} \ sigma _ {1}, \ quad b = \ sigma _ {1} \ sigma _ {2}}

a=\sigma _{1}\sigma _{2}\sigma _{1},\quad b=\sigma _{1}\sigma _{2}

Из соотношений кос следует, что $a 2 = b 3 {\ displaystyle a ^ {2} = b ^ {3}}$ $a^{2}=b^{3}$ . Обозначая этот последний продукт как $c {\ displaystyle c}$ $c$ , можно проверить из соотношений кос, что

σ 1 c σ 1 - 1 = σ 2 c σ 2 - 1 = c { \ displaystyle \ sigma _ {1} c \ sigma _ {1} ^ {- 1} = \ sigma _ {2} c \ sigma _ {2} ^ {- 1} = c}

\sigma_1 c \sigma_1^{-1} = \sigma_2 c \sigma_2^{-1}=c

, подразумевая, что $c {\ displaystyle c}$ $c$ находится в центре $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ . Пусть $C {\ displaystyle C}$ $C$ обозначает подгруппу из $B 3 {\ displaystyle B_ {3}}$ $B_{3}$ сгенерированную с помощью c, поскольку C ⊂ Z (B 3), это нормальная подгруппа, и можно взять факторгруппу B3/ C. Мы утверждаем, что B 3 / C ≅ PSL (2, Z ); этому изоморфизму можно придать явный вид. смежные классы σ1C и σ 2 C отображаются в

σ 1 C ↦ R = [1 1 0 1] σ 2 C ↦ L - 1 = [1 0 - 1 1 ] {\ displaystyle \ sigma _ {1} C \ mapsto R = {\ begin {bmatrix} 1 1 \\ 0 1 \ end {bmatrix}} \ qquad \ sigma _ {2} C \ mapsto L ^ {- 1} = { \ begin {bmatrix} 1 0 \\ - 1 1 \ end {bmatrix}}}

\sigma_1C \mapsto R=\begin{bmatrix}1 1 \\ 0 1 \end{bmatrix} \qquad \sigma_2C \mapsto L^{-1}=\begin{bmatrix}1 0 \\ -1 1 \end{bmatrix}

где L и R - стандартные ходы влево и вправо на дереве Штерна – Броко ; хорошо известно, что эти ходы порождают модульную группу.

В качестве альтернативы, одно общее представление для модульной группы:

⟨v, p | v 2 = p 3 = 1⟩ {\ displaystyle \ langle v, p \, | \, v ^ {2} = p ^ {3} = 1 \ rangle}

\langle v,p\, |\, v^2=p^3=1\rangle

где

v = [0 1 - 1 0], p = [0 1 - 1 1]. {\ displaystyle v = {\ begin {bmatrix} 0 1 \\ - 1 0 \ end {bmatrix}}, \ qquad p = {\ begin {bmatrix} 0 1 \\ - 1 1 \ end {bmatrix}}.}

v=\begin{bmatrix}0 1 \\ -1 0 \end{bmatrix}, \qquad p=\begin{bmatrix}0 1 \\ -1 1 \end{bmatrix}.

Отображение a в v и b в p дает гомоморфизм сюръективной группы B 3 → PSL (2, Z ).

Центр B 3 равен C, что является следствием того факта, что c находится в центре, модулярная группа имеет тривиальный центр и указанный выше сюръективный гомоморфизм имеет ядро C.

Связь с группой классов отображения и классификация кос

Группа кос B n может быть показана как изоморфная группе классов отображения проколотого диска с n проколами. Это легче всего визуализировать, если представить, что каждый прокол связан веревкой с границей диска; каждый гомоморфизм отображения, который переставляет два прокола, можно затем рассматривать как гомотопию струн, то есть сплетение этих струн.

Посредством этой групповой интерпретации кос, каждая коса может быть классифицирована как периодическая, сводимая или псевдоаносовская.

Связь с теорией узлов

Если коса задана и один соединяет первый левый элемент с первым правым элементом с помощью новой строки, второй левый элемент со вторым правым элементом и т. д. (без создания каких-либо кос в новых строках), получается ссылка, а иногда и узел . Теорема Александера в теории кос утверждает, что верно и обратное: каждый узел и каждое звено возникают таким образом как минимум из одна коса; такую косу можно получить, перерезав звено. Поскольку косы могут быть конкретно заданы как слова в генераторах σ i, это часто является предпочтительным методом завязывания узлов в компьютерные программы.

Вычислительные аспекты

Проблема слов для связей кос является эффективно решаемой, и существует нормальная форма для элементов B n в терминах образующих σ 1,..., σ n − 1. (По сути, вычисление нормальной формы косы - это алгебраический аналог «вытягивания прядей», как показано во втором наборе изображений выше.) Бесплатная система компьютерной алгебры GAP может выполнять вычисления в B n, если элементы даны в терминах этих генераторов. Также существует пакет под названием CHEVIE for GAP3 со специальной поддержкой групп кос. Проблема слов также эффективно решается с помощью представления Лоуренса – Краммера.

Помимо проблемы слов, существует несколько известных сложных вычислительных проблем, которые могут реализовать группы кос, приложения в криптографии были предложено.

Действия

По аналогии с действием симметрической группы перестановками, в различных математических установках существует естественное действие группы кос на n наборов объектов или на n -свернутое тензорное произведение, которое включает в себя некоторые "изгибы". Рассмотрим произвольную группу G и пусть X будет множеством всех n-кортежей элементов G, произведение которых является единичным элементом группы G. Тогда B nдействует на X следующим образом :

σ i (x 1,…, xi - 1, xi, xi + 1,…, xn) = (x 1,…, xi - 1, xi + 1, xi + 1 - 1 xixi + 1, xi + 2,…, xn). {\ displaystyle \ sigma _ {i} \ left (x_ {1}, \ ldots, x_ {i-1}, x_ {i}, x_ {i + 1}, \ ldots, x_ {n} \ right) = \ left (x_ {1}, \ ldots, x_ {i-1}, x_ {i + 1}, x_ {i + 1} ^ {- 1} x_ {i} x_ {i + 1}, x_ {i +2}, \ ldots, x_ {n} \ right).}

\sigma_i \left (x_1,\ldots,x_{i-1},x_i, x_{i+1},\ldots, x_n \right)= \left (x_1,\ldots, x_{i-1}, x_{i+1}, x_{i+1}^{-1}x_i x_{i+1}, x_{i+2},\ldots,x_n \right).

Таким образом, элементы x i и x i + 1 меняются местами и, кроме того, x i скручивается с помощью внутреннего автоморфизма , соответствующего x i + 1 - это гарантирует, что произведение компонентов x остается единичным элементом. Можно проверить, что отношения групп кос выполняются, и эта формула действительно определяет групповое действие B n на X. В качестве другого примера, сплетенная моноидальная категория является моноидальная категория с действием группы кос. Такие структуры играют важную роль в современной математической физике и приводят к квантовым инвариантам узлов.

Представления

Элементы группы кос B n могут быть более конкретно представлены матрицами. Одним из классических таких представлений является представление Бурау, где матричные элементы представляют собой полиномы Лорана одной переменной . Вопрос о том, является ли представление Бурау точным, был давним, но ответ оказался отрицательным для n ≥ 5. В целом, это была большая открытая проблема, являются ли группы кос линейными.. В 1990 году Рут Лоуренс описала семейство более общих «представлений Лоуренса», зависящих от нескольких параметров. В 1996 году Четан Наяк и Франк Вильчек постулировали, что по аналогии с проективными представлениями SO (3) проективные представления группы кос имеют физический смысл для некоторых квазичастиц в дробном квантовом эффекте Холла.. Примерно в 2001 году Стивен Бигелоу и Даан Краммер независимо друг от друга доказали, что все группы кос линейны. В их работе использовалось представление Лоуренса – Краммера размерности $n (n - 1) / 2 {\ displaystyle n (n-1) / 2}$ $n(n-1)/2$ в зависимости от переменных q и т. Путем соответствующей специализации этих переменных группа кос $B n {\ displaystyle B_ {n}}$ $B_{n}$ может быть реализована как подгруппа общей линейной группы над комплексные числа.

Бесконечно порождаемые группы кос

Есть много способов обобщить это понятие на бесконечное количество прядей. Самый простой способ - взять прямой предел групп кос, где прикрепляемые карты $f: B n → B n + 1 {\ displaystyle f \ двоеточие B_ {n} \ to B_ {n +1}}$ $f\colon B_{n}\to B_{n+1}$ отправить $n - 1 {\ displaystyle n-1}$ $n-1$ генераторы $B n {\ displaystyle B_ {n}}$ $B_{{n}}$ к первому $n - 1 {\ displaystyle n-1}$ $n-1$ генераторы $B n + 1 {\ displaystyle B_ {n + 1}}$ $B_{n+1}$ ( т.е. прикрепив тривиальную прядь). Пол Фабель показал, что есть две топологии , которые могут быть наложены на результирующую группу, каждая из которых завершение дает другую группу. Одна очень ручная группа и изоморфна группе классов отображения бесконечно проколотого диска - дискретному набору проколов, ограничивающемуся границей диска.

Вторая группа может считаться так же, как с конечными группами кос. Поместите прядь в каждую из точек $(0, 1 / n) {\ displaystyle (0,1 / n)}$ $(0,1/n)$ и на набор всех кос, где коса определяется как набор путей от точек $(0, 1 / n, 0) {\ displaystyle (0,1 / n, 0)}$ $(0,1/n,0)$ до точек $(0, 1 / n, 1) {\ displaystyle (0,1 / n, 1)}$ $(0,1/n,1)$ , так что функция дает перестановку на конечных точках - изоморфна этой более дикой группе. Интересен тот факт, что группа чистых кос в этой группе изоморфна как обратному пределу конечных групп чистых кос $P n {\ displaystyle P_ {n}}$ $P_{n}$ , так и в фундаментальную группу куба Гильберта за вычетом множества

{(xi) i ∈ N ∣ xi = xj для некоторого i ≠ j}. {\ displaystyle \ {(x_ {i}) _ {i \ in \ mathbb {N}} \ mid x_ {i} = x_ {j} {\ text {для некоторых}} i \ neq j \}.}

\{(x_{i})_{i\in \mathbb {N} }\mid x_{i}=x_{j}{\text{ for some }}i\neq j\}.

Когомологии

Когомологии группы $G {\ displaystyle G}$ $G$ определяются как когомологии соответствующих Eilenberg – MacLane классифицирующее пространство, $K (G, 1) {\ displaystyle K (G, 1)}$ $K(G,1)$ , которое является однозначно определенным комплексом CW автор $G {\ displaystyle G}$ $G$ вплоть до гомотопии. Классифицирующее пространство для группы кос $B n {\ displaystyle B_ {n}}$ $B_{n}$ - это nнеупорядоченное пространство конфигурации $R 2. {\ displaystyle \ mathbb {R} ^ {2}}$ $\R^2$ , то есть набор из $n {\ displaystyle n}$ $n$ различных неупорядоченных точек на плоскости:

UConf n ⁡ (R 2) = {{u 1,..., un}: ui ∈ R 2, ui ≠ uj для я ≠ j} {\ displaystyle \ operatorname {UConf} _ {n} (\ mathbb {R} ^ {2}) = \ {\ {u_ {1},..., u_ {n} \}: u_ {i} \ in \ mathbb {R} ^ {2}, u_ {i} \ neq u_ {j} {\ text {for}} i \ neq j \} }

\operatorname {UConf} _{n}(\mathbb {R} ^{2})=\{\{u_{1},...,u_{n}\}:u_{i}\in \mathbb {R} ^{2},u_{i}\neq u_{j}{\text{ for }}i\neq j\}

Таким образом, по определению

H ∗ (B n) = H ∗ (K (B n, 1)) = H ∗ (UConf n ⁡ (R 2)). {\ displaystyle H ^ {*} (B_ {n}) = H ^ {*} (K (B_ {n}, 1)) = H ^ {*} (\ operatorname {UConf} _ {n} (\ mathbb {R} ^ {2})).}

H^{*}(B_{n})=H^{*}(K(B_{n},1))=H^{*}( \operatorname {UConf} _{n}(\mathbb {R} ^{2})).

Вычисления коэффициентов в $Z / 2 Z {\ displaystyle \ mathbb {Z} / 2 \ mathbb {Z}}$ $\mathbb {Z} /2\mathbb {Z}$ могут быть найдено у Фукса (1970).

Точно так же классифицирующим пространством для чистой группы кос $P n {\ displaystyle P_ {n}}$ $P_{n}$ является $Conf n ⁡ ( R 2) {\ displaystyle \ operatorname {Conf} _ {n} (\ mathbb {R} ^ {2})}$ $\operatorname {Conf} _{n}(\mathbb {R} ^{2})$ , nупорядоченное пространство конфигурации из $R 2 {\ displaystyle \ mathbb {R} ^ {2}}$ $\R^2$ . В 1968 году Владимир Арнольд показал, что интегральные когомологии чистой группы кос $P n {\ displaystyle P_ {n}}$ $P_{n}$ являются частным от внешней алгебры, порожденный набором классов первой степени $ω ij 1 ≤ i < j ≤ n {\displaystyle \omega _{ij}\;\;1\leq i$ $\omega _{ij}\;\;1\leq i<j\leq n$ , с учетом соотношений

ω k, ℓ ω ℓ, m + ω ℓ, m ω m, k + ω м, К ω К, ℓ знак равно 0. {\ Displaystyle \ omega _ {k, \ ell} \ omega _ {\ ell, m} + \ omega _ {\ ell, m} \ omega _ {m, k } + \ omega _ {m, k} \ omega _ {k, \ ell} = 0.}

\omega _{k,\ell }\omega _{\ell,m}+\omega _{\ell,m}\omega _{m,k}+\omega _{m,k}\omega _{k,\ell }=0.

См. также

Группа Артина – Титса
Плетеная моноидальная категория
Плетенное векторное пространство
Плетеная алгебра Хопфа
Программное обеспечение для изменения звонков - как программное обеспечение использует теорию кос для моделирования шаблонов звонков
Теория узлов
Некоммутативная криптография

Ссылки

^Вайсштейн, Эрик. "Группа кос". Вольфрам Матворлд.
^Коэн, Дэниел; Сучиу, Александр (1997). "Монодромия кос плоских алгебраических кривых и гиперплоскостных схем". Commentarii Mathematici Helvetici. 72 (2): 285–315. arXiv : alg-geom / 9608001. doi : 10.1007 / s000140050017.
^Boyland, Philip L.; Ареф, Хасан; Стремлер, Марк А. (2000), «Топологическая жидкостная механика перемешивания» (PDF), Journal of Fluid Mechanics, 403 (1): 277–304, Bibcode : 2000JFM... 403..277B, doi : 10.1017 / S0022112099007107, MR 1742169, заархивировано с оригинала (PDF) 26 июля 2011 г.
^Гуйяр, Эммануэль; Тиффо, Жан-Люк; Финн, Мэтью Д. (2006), «Топологическое смешение с призрачными стержнями», Physical Review E, 73 (3): 036311, arXiv : nlin / 0510075, Bibcode : 2006PhRvE..73c6311G, doi : 10.1103 / PhysRevE.73.036311, MR 2231368
^Stremler, Mark A.; Росс, Шейн Д.; Гровер, Пиюш; Кумар, Панкадж (2011), «Топологический хаос и периодическое плетение почти циклических множеств», Physical Review Letters, 106 (11): 114101, Bibcode : 2011PhRvL.106k4101S, doi : 10.1103 / PhysRevLett.106.114101
^Марков, Андрей (1935), "Über die freie Äquivalenz der geschlossenen Zöpfe ", Recueil Mathématique de la Société Mathématique de Moscou (на немецком и русском языках), 1 : 73–78
^Ламбропулу, София; Рурк, Колин П. (1997), «Теорема Маркова в 3-многообразиях», Топология и ее приложения, 78(1-2): 95–122, arXiv : math / 0405498, doi : 10.1016 / S0166-8641 (96) 00151-4, MR 1465027
^Бирман, Джоан С. ( 1974), Braids, Links, and mapping class groups, Annals of Mathematics Studies, 82, Princeton, NJ: Princeton University Press, ISBN 978 -0-691-08149-6, MR 0375281
^Вайсштейн, Эрик У. (август 2014 г.). "Указатель кос". MathWorld - Интернет-ресурс Wolfram. Проверено 6 августа 2014 г.
^Магнус, Вильгельм (1974). «Группы кос: обзор». Труды Второй Международной конференции по теории групп. Конспект лекций по математике. 372 . Springer. С. 463–487. ISBN 978-3-540-06845-7.
^ Артин, Эмиль (1947). «Теория кос». Анналы математики. 48(1): 101–126. DOI : 10.2307 / 1969218. JSTOR 1969218.
^Фокс, Ральф ; Нойвирт, Ли (1962). "Группы кос". Mathematica Scandinavica. 10 : 119–126. doi : 10.7146 / math.scand.a-10518. MR 0150755.
^Грист, Роберт (1 декабря 2009 г.). «Конфигурационные пространства, косы и робототехника». Косички. Серия лекций, Институт математических наук, Национальный университет Сингапура. 19. World Scientific. С. 263–304. doi : 10.1142 / 9789814291415_0004. ISBN 9789814291408.
^Фукс, Дмитрий Б. (1970). «Когомологии группы кос mod 2». Функциональный анализ и его приложения. 4 (2): 143–151. doi : 10.1007 / BF01094491. MR 0274463.
^Арнольд, Владимир (1969). «Кольцо когомологий группы раскрашенных кос» (PDF). Мат. Заметки. 5 : 227–231. MR 0242196.

Дополнительная литература

Внешние ссылки

«Группа оплетки». PlanetMath.
CRAG: CRyptography and Groups at Algebraic Cryptography Center Contains extensive library for computations with Braid Groups
[1] Visual Group Theory, Lecture 1.3: Groups in science, art, and mathematics
Fabel, Paul (2005), "Completing Artin's braid group on infinitely many strands", Journal of Knot Theory and Its Ramifications, 14(8): 979–991, arXiv :math/0201303, doi :10.1142/S0218216505004196, MR 2196643
Fabel, Paul (2006), "The mapping class group of a disk with infinitely many holes", Journal of Knot Theory and Its Ramifications, 15(1): 21–29, arXiv :math/0303042, doi :10.1142/S0218216506004324, MR 2204494
Chernavskii, A.V. (2001) [1994], Encyclopedia of Mathematics, EMS Press
Bigelow, Stephen. "Exploration of B5 Java applet".
Nayak, Chetan; Wilczek, Frank (1996), "$2n$ Quasihole States Realize $2^{n-1}$-Dimensional Spinor Braiding Statistics in Paired Quantum Hall States", Nuclear Physics B, 479(3): 529–553, arXiv :cond-mat/9605145, Bibcode :1996NuPhB.479..529N, doi :10.1016/0550-3213(96)00430-0 — connection of projective braid group representations to the fractional quantum Hall effect
Presentation for FradkinFest by Chetan V. Nayak [2]
Read, N. (2003), "Nonabelian braid statistics versus projective permutation statistics", Journal of Mathematical Physics, 44(2): 558–563, arXiv :hep-th/0201240, Bibcode :2003JMP....44..558R, doi :10.1063/1.1530369 — criticism of the reality of Wilczek-Nayak representation
Lipmaa, Helger, Cryptography and Braid Groups page, archived from the original on 3 August 2009
Braid group: List of Authority Articles on arxiv.org.
"Braids - the movie" A movie in computer graphics to explain some of braid theory (group presentation, word problem, closed braids and links, braids as motions of points in the plane).
WINNER of Science magazine 2017 Dance Your PhD: Representations of the Braid Groups. Nancy Scherich.
Behind the Math of Dance Your PhD, Part 1: The Braid Groups. Nancy Scherich. Explanation of braid groups as used in the movie.