Формулировка фазового пространства

Формулировка квантовой механики

Формулировка фазового пространства квантовой механики помещает переменные position и momentum в равное положение в фазовом пространстве. Напротив, изображение Шредингера использует представления положения или импульса (см. Также пространство положения и импульса ). Две ключевые особенности формулировки фазового пространства заключаются в том, что квантовое состояние описывается распределением квазивероятностей (вместо волновой функции, вектора состояния или матрица плотности ), а операторное умножение заменяется звездным произведением.

Теория была полностью развита Хильбрандом Греневольдом в 1946 году в его докторской диссертации, и независимо - Джо Мойал, каждый из которых основан на более ранних идеях Германа Вейля и Юджина Вигнера.

Главное преимущество формулировки фазового пространства в том, что она делает квантовую механику похожей на Гамильтонова механика, избегая операторного формализма, тем самым «освобождая» квантование от «бремени» гильбертова пространства ». Эта формулировка является статистической по своей природе и предлагает логические связи между квантовой механикой и классической статистической механикой, обеспечивая естественное сравнение между ними (см. классический предел ). Квантовой механике в фазовом пространстве часто отдают предпочтение в определенных приложениях квантовой оптики (см. оптическое фазовое пространство ) или в исследовании декогеренции и в ряде специализированных технических

Концептуальные идеи, лежащие в основе развития квантовой механики в фазовом пространстве, разветвились на математические ответвления, такие как деформационно-квантование Концевича (см. квантование Концевича) формула ) и некоммутативная геометрия.

• 1 Распределение в фазовом пространстве
• 2 Звездное произведение
• 3 Временная эволюция
• 4 Примеры
  • 4.1 Простой гармонический осциллятор
  • 4.2 Угловой момент свободной частицы
  • 4.3 Потенциал Морзе
  • 4.4 Квантовое туннелирование
  • 4.5 Четвертый потенциал
  • 4.6 Состояние кота Шредингера
• 5 Ссылки

Фаза -пространственное распределение f (x, p) квантового состояния является распределением квазивероятностей. В формулировке фазового пространства распределение фазового пространства можно рассматривать как фундаментальное, примитивное описание квантовой системы без какой-либо ссылки на волновые функции или матрицы плотности.

Существует несколько различных способов представления распределение, все взаимосвязано. Наиболее примечательным является представление Вигнера, W (x, p), обнаруженное первым. Другие представления (примерно в порядке убывания распространенности в литературе) включают представления Глаубера – Сударшана P, Хусими Q, Кирквуда – Рихачека, Мехта, Ривье и Борна – Джордана. Эти альтернативы наиболее полезны, когда гамильтониан принимает конкретную форму, такую ​​как нормальный порядок для P-представления Глаубера – Сударшана. Поскольку представление Вигнера является наиболее распространенным, эта статья обычно придерживается его, если не указано иное.

Распределение в фазовом пространстве обладает свойствами, аналогичными плотности вероятности в 2n-мерном фазовом пространстве. Например, это действительное значение, в отличие от обычно комплексной волновой функции. Мы можем понять вероятность нахождения в пределах позиционного интервала, например, интегрировав функцию Вигнера по всем импульсам и по позиционному интервалу:

$P\; \; [a\; \le \; X\; \le \; b]\; =\; \int \; ab\; \int \; -\; \infty \; \infty \; W\; (\; х,\; р)\; dpdx.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{P\}\; [a\; \backslash \; leq\; X\; \backslash \; leq\; b]\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; W\; (x,\; p)\; \backslash ,\; dp\; \backslash ,\; dx.\}$

Если Â (x, p) - оператор, представляющий наблюдаемую, он может быть отображен в фазовое пространство как A (x, p) с помощью преобразования Вигнера. И наоборот, этот оператор может быть восстановлен с помощью преобразования Вейля.

. Ожидаемое значение наблюдаемой относительно распределения в фазовом пространстве равно

$⟨A\; ^⟩\; =\; \int \; A\; (x,\; p)\; W\; (x,\; п)\; dpdx.\; \{\backslash \; displaystyle\; \backslash \; langle\; \{\backslash \; hat\; \{A\}\}\; \backslash \; rangle\; =\; \backslash \; int\; A\; (x,\; p)\; W\; (x,\; p)\; \backslash ,\; dp\; \backslash ,\; dx.\}$

Однако следует предостеречь: несмотря на схожесть по внешнему виду W (x, p) не является подлинным совместным распределением вероятностей, поскольку области под ним не представляют взаимоисключающие состояния, как требуется в третьей аксиоме теории вероятностей. Более того, он может, как правило, принимать отрицательные значения даже для чистых состояний, за единственным исключением (необязательно сжатых ) когерентных состояний, в нарушение первая аксиома.

Доказуемо, что области с таким отрицательным значением являются «маленькими»: они не могут распространяться на компактные области размером более нескольких и, следовательно, исчезают в классическом пределе. Они защищены принципом неопределенности, который не допускает точной локализации в областях фазового пространства меньше, и, таким образом, делает такие «отрицательные вероятности» менее парадоксальными. Если левую часть уравнения следует интерпретировать как значение математического ожидания в гильбертовом пространстве относительно оператора, то в контексте квантовой оптики это уравнение известно как теорема оптической эквивалентности. (Подробнее о свойствах и интерпретации функции Вигнера см. Ее основную статью.)

Альтернативный фазовый подход к квантовой механике направлен на определение волновой функции (а не просто плотность квазивероятностей) на фазовом пространстве, обычно с помощью преобразования Сегала – Баргмана. Чтобы быть совместимым с принципом неопределенности, волновая функция фазового пространства не может быть произвольной функцией, иначе она может быть локализована в сколь угодно малой области фазового пространства. Скорее преобразование Сегала – Баргмана представляет собой голоморфную функцию от $x\; +\; i\; p\; \{\backslash \; displaystyle\; x\; +\; ip\}$. С волновой функцией в фазовом пространстве связана плотность квазивероятностей; это представление Husimi Q волновой функции положения.

Основным некоммутативным бинарным оператором в формулировке фазового пространства, который заменяет стандартный оператор умножения, является звездное произведение , представленное символом ★. Каждое представление распределения фазового пространства имеет свой характерный звездный продукт. Для конкретности мы ограничим это обсуждение звездным произведением, относящимся к представлению Вигнера-Вейля.

Для удобства обозначений мы вводим понятие левой и правой производных. Для пары функций f и g левая и правая производные определяются как

$f\; \partial \; \leftarrow \; x\; g\; =\; \partial \; f\; \partial \; x\; \cdot \; g\; f\; \partial \; \to \; x\; g\; =\; f\; \cdot \; \partial \; g\; \partial \; x.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; f\; \{\backslash \; overleftarrow\; \{\backslash \; partial\}\}\; \_\; \{x\}\; g\; =\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; x\}\}\; \backslash \; cdot\; g\; \backslash \backslash \; [5pt]\; f\; \{\backslash \; overrightarrow\; \{\backslash \; partial\}\}\; \_\; \{x\}\; g\; =\; f\; \backslash \; cdot\; \{\backslash \; frac\; \{\backslash \; partial\; g\}\; \{\backslash \; partial\; x\}\}.\; \backslash \; end\; \{align\}\}\}$

Дифференциальное определение звездный продукт

$е\; \star \; g\; =\; е\; ехр\; \; (я\; \hslash \; 2\; (\partial \; \leftarrow \; x\; \partial \; \to \; p\; -\; \partial \; \leftarrow \; p\; \partial \; \to \; x))\; g\; \{\backslash \; displaystyle\; f\; \backslash \; star\; g\; =\; f\; \backslash ,\; \backslash \; exp\; \{\backslash \; left\; (\{\backslash \; frac\; \{i\; \backslash \; hbar\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; overleftarrow\; \{\backslash \; partial\}\}\; \_\; \{x\}\; \{\backslash \; overrightarrow\; \{\backslash \; partial\}\}\; \_\; \{p\}\; -\; \{\backslash \; overleftarrow\; \{\backslash \; partial\}\}\; \_\; \{p\}\; \{\backslash \; overrightarrow\; \{\backslash \; partial\}\}\; \_\; \{x\}\; \backslash \; right)\; \backslash \; right)\}\; \backslash ,\; g\}$

где аргумент экспоненциальной функции можно интерпретировать как степенной ряд. Дополнительные дифференциальные соотношения позволяют записать это в терминах изменения аргументов f и g:

$(f ⋆ g) (x, p) = f (x + i ℏ 2 ∂ → p, p - i ℏ 2 ∂ → x) ⋅ g (x, p) = f (x, p) ⋅ g (x - i ℏ 2 ∂ ← p, p + i ℏ 2 ∂ ← x) = f (x + i ℏ 2 ∂ → p, p) ⋅ g (x - i ℏ 2 ∂ ← p, p) = f (x, p - i ℏ 2 ∂ → x) ⋅ g (x, p + i ℏ 2 ∂ ← x). {\ displaystyle {\ begin {align} (е \ звезда g) (x, p) = f \ left (x + {\ tfrac {i \ hbar} {2}} {\ overrightarrow {\ partial}} _ {p }, p - {\ tfrac {i \ hbar} {2}} {\ overrightarrow {\ partial}} _ {x} \ right) \ cdot g (x, p) \\ = f (x, p) \ cdot g \ left (x - {\ tfrac {i \ hbar} {2}} {\ overleftarrow {\ partial}} _ {p}, p + {\ tfrac {i \ hbar} {2}} {\ overleftarrow {\ partial}} _ {x} \ right) \\ = f \ left (x + {\ tfrac {i \ hbar} {2}} {\ overrightarrow {\ partial}} _ {p}, p \ right) \ cdot g \ left (x - {\ tfrac {i \ hbar} {2}} {\ overleftarrow {\ partial}} _ {p}, p \ right) \\ = f \ left (x, p - {\ tfrac {i \ hbar} {2}} {\ overrightarrow {\ partial}} _ {x} \ right) \ cdot g \ left (x, p + {\ tfrac {i \ hbar} {2}} {\ overleftarrow {\ partial}} _ {x} \ right). \ end {выравнивание}}}$

Также возможно определить ★ -продукт в интегральной форме свертки, по существу, через Фурье преобразование :

$(f\; \star \; g)\; (x,\; p)\; =\; 1\; \pi \; 2\; \hslash \; 2\; \int \; f\; (x\; +\; x\; \prime ,\; p\; +\; p\; \prime )\; g\; (x\; +\; x\; ″,\; p\; +\; p\; ″)\; exp\; \; (2\; i\; \hslash \; (x\; \prime \; p\; ″\; -\; x\; ″\; p\; \prime ))\; dx\; \prime \; dp\; \prime \; dx\; ″\; dp\; ″.\; \{\backslash \; Displaystyle\; (е\; \backslash \; звезда\; г)\; (х,\; р)\; =\; \{\backslash \; гидроразрыва\; \{1\}\; \{\backslash \; pi\; ^\; \{2\}\; \backslash \; hbar\; ^\; \{2\}\}\}\; \backslash ,\; \backslash \; int\; f\; (х\; +\; х\; \text{'},\; р\; +\; р\; \text{'})\; \backslash ,\; g\; (x\; +\; x\text{'}\; \text{'},\; p\; +\; p\text{'}\; \text{'})\; \backslash ,\; \backslash \; exp\; \{\backslash \; left\; (\{\backslash \; tfrac\; \{2i\}\; \{\backslash \; hbar\}\}\; (x\text{'}p\text{'}\; \text{'}-\; x\text{'}\text{'}p\text{'})\; \backslash \; right)\}\; \backslash ,\; dx\text{'}dp\text{'}dx\text{'}\text{'}dp\; \text{'}\text{'}\; ~.\}$

(Таким образом, например, гауссианы составляют гиперболически,

$exp\; \; (-\; a\; (x\; 2\; +\; p\; 2))\; \star \; ехр\; \; (-\; б\; (Икс\; 2\; +\; п\; 2))\; знак\; равно\; 1\; 1\; +\; \hslash \; 2\; ab\; ехр\; \; (-\; a\; +\; b\; 1\; +\; \hslash \; 2\; ab\; (x\; 2\; +\; p\; 2)),\; \{\backslash \; Displaystyle\; \backslash \; ехр\; \backslash \; влево\; (-\; \{a\}\; (x\; ^\; \{2\}\; +\; p\; ^\; \{2\})\; \backslash \; right)\; ~\; \backslash \; star\; ~\; \backslash \; exp\; \backslash \; left\; (-\; \{b\}\; (x\; ^\; \{2\}\; +\; p\; ^\; \{2\})\; \backslash \; right)\; =\; \{\; 1\; \backslash \; over\; 1+\; \backslash \; hbar\; ^\; \{2\}\; ab\}\; \backslash \; exp\; \backslash \; left\; (-\; \{a\; +\; b\; \backslash \; over\; 1+\; \backslash \; hbar\; ^\; \{2\}\; ab\}\; (x\; ^\; \{2\}\; +\; p\; ^\; \{2\})\; \backslash \; right),\}$

или

$\delta \; (x)\; \star \; \delta \; (p)\; =\; 2\; час\; exp\; \; (2\; ixp\; \hslash ),\; \{\backslash \; displaystyle\; \backslash \; delta\; (x)\; ~\; \backslash \; star\; ~\; \backslash \; delta\; (p)\; =\; \{2\; \backslash \; over\; h\}\; \backslash \; exp\; \backslash \; left\; (2i\; \{xp\; \backslash \; over\; \backslash \; hbar\}\; \backslash \; right),\}$

и т.д.)

Распределения энергии собственного состояния известны как звездные состояния, ★ -ген-состояния, звездообразующие функции или ★ -ген-функции и связанные с ними энергии известны как звездные значения или ★ -ген-значения. Они решаются аналогично не зависящему от времени уравнению Шредингера с помощью уравнения ★ -genvalue,

$H\; \star \; W\; =\; E\; \cdot \; W,\; \{\backslash \; displaystyle\; H\; \backslash \; star\; W\; =\; E\; \backslash \; cdot\; W,\}$

где H - гамильтониан, функция простого фазового пространства, чаще всего идентичная классическому гамильтониану.

Временная эволюция распределения фазового пространства задается квантовой модификацией потока Лиувилля. Эта формула является результатом применения преобразования Вигнера к версии матрицы плотности квантового уравнения Лиувилля, уравнения фон Неймана.

В любом представлении распределения фазового пространства с связанный с ним звездный продукт, это

$\partial \; е\; \partial \; T\; =\; -\; 1\; я\; f\; (е\; \star \; H\; -\; H\; \star \; f),\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; f\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{i\; \backslash \; hbar\}\}\; \backslash \; left\; (f\; \backslash \; star\; HH\; \backslash \; star\; f\; \backslash \; right),\}$

или, в частности, для функции Вигнера

$\partial \; W\; \partial \; t\; =\; -\; \{\{W,\; H\}\}\; =\; -\; 2\; \hslash \; W\; грех\; \; (\hslash \; 2\; (\partial \; x\; \leftarrow \; \partial \; p\; \to \; -\; \partial \; p\; \leftarrow \; \partial \; x\; \to ))\; H\; =\; -\; \{W,\; H\}\; +\; O\; (\hslash \; 2),\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; W\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \backslash \; \{\backslash \; \{W,\; H\; \backslash \}\; \backslash \}\; =\; -\; \{\backslash \; frac\; \{2\}\; \{\backslash \; hbar\}\}\; W\; \backslash \; sin\; \backslash \; left\; (\{\{\backslash \; frac\; \{\backslash \; hbar\; \}\; \{2\}\}\; (\{\backslash \; overset\; \{\backslash \; leftarrow\}\; \{\backslash \; partial\; \_\; \{x\}\}\}\; \{\backslash \; overset\; \{\backslash \; rightarrow\}\; \{\backslash \; partial\; \_\; \{p\}\}\}\; -\; \{\backslash \; overset\; \{\backslash \; leftarrow\}\; \{\backslash \; partial\; \_\; \{p\}\}\}\; \{\backslash \; overset\; \{\backslash \; rightarrow\}\; \{\backslash \; partial\; \_\; \{x\}\}\})\}\; \backslash \; right)\; \backslash \; H\; =\; -\; \backslash \; \{W,\; H\; \backslash \}\; +\; O\; (\backslash \; hbar\; ^\; \{2\}),\}$

, где {{,}} - скобка Мойала, преобразование Вигнера квантового коммутатора, а {, } - это классическая скобка Пуассона.

Это дает краткую иллюстрацию принципа соответствия : это уравнение явно сводится к классическому уравнению Лиувилля в пределе ħ → 0. В квантовом расширении поток, однако плотность точек в фазовом пространстве не сохраняется; жидкость вероятности кажется "диффузной" и сжимаемой. Поэтому концепция квантовой траектории здесь является деликатным вопросом. Посмотрите фильм о потенциале Морзе ниже, чтобы оценить нелокальность квантового фазового потока.

Примечание. Учитывая ограничения, накладываемые принципом неопределенности на локализацию, Нильс Бор категорически отрицал физическое существование таких траекторий в микроскопическом масштабе. С помощью формальных траекторий в фазовом пространстве проблема временной эволюции функции Вигнера может быть строго решена с использованием метода интегралов по путям и метода квантовых характеристик, хотя в обоих случаях существуют серьезные практические препятствия.

Простой гармонический осциллятор

Распределение квазивероятностей Вигнера F n (u) для простого гармонического осциллятора с a) n = 0, b) n = 1, и c) n = 5.

Гамильтониан для простого гармонического осциллятора в одном пространственном измерении в представлении Вигнера-Вейля равен

$H\; =\; 1\; 2\; m\; \omega \; 2\; x\; 2\; +\; p\; 2\; 2\; m.\; \{\backslash \; displaystyle\; H\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; omega\; ^\; \{2\}\; x\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\; ^\; \{2\}\}\; \{2m\}\}.\}$

★ -значное уравнение для статической функции Вигнера, тогда читается как

$H ⋆ W = (1 2 m ω 2 x 2 + p 2 2 m) ⋆ W = (1 2 m ω 2 (x + i ℏ 2 ∂ → p) 2 + 1 2 m (p - i ℏ 2 ∂ → x) 2) W = (1 2 m ω 2 (x 2 - ℏ 2 4 ∂ → p 2) + 1 2 m (p 2 - ℏ 2 4 ∂ → x 2)) W + i ℏ 2 (m ω 2 x ∂ → p - pm ∂ → x) W = E ⋅ W. {\ displaystyle {\ begin {align} H \ star W = {} \ left ({\ frac {1} {2}} m \ omega ^ {2} x ^ {2} + {\ frac {p ^ { 2}} {2m}} \ right) \ star W \\ [4pt] = {} \ left ({\ frac {1} {2}} m \ omega ^ {2} \ left (x + {\ frac { i \ hbar} {2}} {\ stackrel {\ rightarrow} {\ partial}} _ {p} \ right) ^ {2} + {\ frac {1} {2m}} \ left (p - {\ frac {i \ hbar} {2}} {\ stackrel {\ rightarrow} {\ partial}} _ {x} \ right) ^ {2} \ right) ~ W \\ [4pt] = {} \ left ({ \ frac {1} {2}} m \ omega ^ {2} \ left (x ^ {2} - {\ frac {\ hbar ^ {2}} {4}} {\ stackrel {\ rightarrow} {\ partial }} _ {p} ^ {2} \ right) + {\ frac {1} {2m}} \ left (p ^ {2} - {\ frac {\ hbar ^ {2}} {4}} {\ stackrel {\ rightarrow} {\ partial}} _ {x} ^ {2} \ right) \ right) ~ W \\ [4pt] {} + {\ frac {i \ hbar} {2}} \ left ( m \ omega ^ {2} x {\ stackrel {\ rightarrow} {\ partial}} _ {p} - {\ frac {p} {m}} {\ stackrel {\ rightarrow} {\ partial}} _ {x } \ right) ~ W \\ [4pt] = {} E \ cdot W. \ end {align}}}$

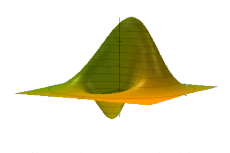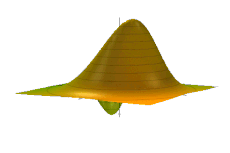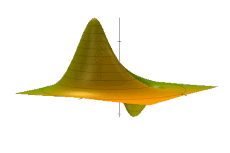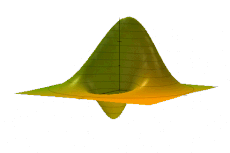
Временная эволюция комбинированной функции Вигнера основного и 1-го возбужденного состояний для простого гармонического осциллятора. Обратите внимание на жесткое движение в фазовом пространстве, соответствующее обычным колебаниям в координатном пространстве. Функция Вигнера для основного состояния гармонического осциллятора, смещенного от начала фазового пространства, то есть когерентного состояния. Обратите внимание на жесткое вращение, идентичное классическому движению: это особенность SHO, иллюстрирующая принцип соответствия . С веб-сайта общей педагогики. (Щелкните, чтобы оживить.)

Рассмотрим, во-первых, мнимую часть уравнения ★ -ген-значения,

$\hslash \; 2\; (m\; \omega \; 2\; x\; \partial \; п\; \to \; -\; pm\; \partial \; x\; \to )\; \cdot \; W\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; hbar\}\; \{2\}\}\; \backslash \; left\; (m\; \backslash \; omega\; ^\; \{2\}\; x\; \{\backslash \; stackrel\; \{\backslash \; rightarrow\}\; \{\backslash \; partial\; \_\; \{\; p\}\}\}\; -\; \{\backslash \; frac\; \{p\}\; \{m\}\}\; \{\backslash \; stackrel\; \{\backslash \; rightarrow\}\; \{\backslash \; partial\; \_\; \{x\}\}\}\; \backslash \; right)\; \backslash \; cdot\; W\; =\; 0\}$

Это означает, что можно записать ★ -гущения как функции одного аргумента,

$W\; (x,\; p)\; =\; F\; (1\; 2\; m\; \omega \; 2\; x\; 2\; +\; p\; 2\; 2\; m)\; \equiv \; F\; (u).\; \{\backslash \; displaystyle\; W\; (x,\; p)\; =\; F\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; m\; \backslash \; omega\; ^\; \{2\}\; x\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\; ^\; \{2\}\}\; \{2m\})\; \}\; \backslash \; right)\; \backslash \; Equiv\; F\; (u).\}$

С такой заменой переменных можно записать действительную часть уравнения ★ -жен-значения в форме модифицированного уравнения Лагерра ( не уравнение Эрмита !), в решении которого используются многочлены Лагерра as

$F\; n\; (u)\; =\; (-\; 1)\; n\; \pi \; \hslash \; L\; n\; (4\; u\; \hslash \; \omega )\; e\; -\; 2\; u\; /\; \hslash \; \omega ,\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (u)\; =\; \{\backslash \; frac\; \{(-1)\; ^\; \{n\}\}\; \{\backslash \; pi\; \backslash \; hbar\}\}\; L\_\; \{n\}\; \backslash \; left\; (4\; \{\backslash \; frac\; \{u\}\; \{\backslash \; hbar\; \backslash \; omega\}\}\; \backslash \; right)\; e\; ^\; \{-\; 2u\; /\; \backslash \; hbar\; \backslash \; omega\}\; ~,\}$

, представленный Гроенвольдом в его статье, с соответствующими ★ -значениями

$E\; n\; =\; \hslash \; \omega \; (n\; +\; 1\; 2).\; \{\backslash \; displaystyle\; E\_\; \{n\}\; =\; \backslash \; hbar\; \backslash \; omega\; \backslash \; left\; (n\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; right)\; ~.\}$

Для гармонического осциллятора временная эволюция произвольного распределения Вигнера проста. Начальное W (x, p; t = 0) = F (u) эволюционирует по вышеуказанному уравнению эволюции, управляемому гамильтонианом осциллятора, заданным путем простого жесткого вращения в фазовом пространстве,

$W\; (x,\; p;\; t)\; =\; W\; (m\; \omega \; x\; cos\; \; \omega \; t\; -\; p\; sin\; \; \omega \; t,\; p\; cos\; \; \omega \; t\; +\; \omega \; mx\; sin\; \; \omega \; t;\; 0).\; \{\backslash \; Displaystyle\; W\; (Икс,\; п;\; T)\; =\; W\; (м\; \backslash \; омега\; х\; \backslash \; соз\; \backslash \; омега\; тп\; \backslash \; грех\; \backslash \; омега\; т,\; ~\; р\; \backslash \; соз\; \backslash \; омега\; т\; +\; \backslash \; омега\; мх\; \backslash \; грех\; \backslash \; омега\; т;\; 0)\; ~.\}$

Как правило, «выпуклость» (или когерентное состояние) энергии E ≫ ħω может представлять макроскопическую величину и выглядеть как классический объект, равномерно вращающийся в фазовом пространстве, простой механический осциллятор (см. Анимированные рисунки). Интегрирование по всем фазам (начальные положения при t = 0) таких объектов, непрерывный «частокол», дает не зависящую от времени конфигурацию, аналогичную приведенной выше статической ★ -генстаты F (u), интуитивно понятной визуализации классического предела для систем с большим действием.

Угловой момент свободной частицы

Предположим, что частица изначально находится в минимально неопределенном гауссовом состоянии, с ожидаемые значения положения и импульса оба центрированы в начале координат в фазовом пространстве. Функция Вигнера для такого состояния, свободно распространяющегося, равна

$W\; (x,\; p;\; t)\; =\; 1\; (\pi \; \hslash )\; 3\; exp\; \; (-\; \alpha \; 2\; r\; 2\; -\; p\; 2\; \alpha \; 2\; \hslash \; 2\; (1\; +\; (t\; \tau )\; 2)\; +\; 2\; T\; \hslash \; \tau \; Икс\; \cdot \; п),\; \{\backslash \; Displaystyle\; W\; (\backslash \; mathbf\; \{x\},\; \backslash \; mathbf\; \{p\};\; t)\; =\; \{\backslash \; frac\; \{1\}\; \{(\backslash \; pi\; \backslash \; hbar)\; ^\; \{3\}\}\; \}\; \backslash \; exp\; \{\backslash \; left\; (-\; \backslash \; alpha\; ^\; \{2\}\; r\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{p\; ^\; \{2\}\}\; \{\backslash \; alpha\; ^\; \{2\}\; \backslash \; hbar\; ^\; \{2\}\}\}\; \backslash \; left\; (1+\; \backslash \; left\; (\{\backslash \; frac\; \{t\}\; \{\backslash \; tau\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{2t\}\; \{\backslash \; hbar\; \backslash \; tau\}\}\; \backslash \; mathbf\; \{x\}\; \backslash \; cdot\; \backslash \; mathbf\; \{p\}\; \backslash \; right)\}\; ~,\}$

где α - параметр, описывающий начальную ширину гауссиана, а τ = m / αħ.

Изначально положение и импульсы не коррелированы. Таким образом, в трехмерном пространстве мы ожидаем, что векторы положения и импульса будут в два раза чаще быть перпендикулярными друг другу, чем параллельными.

Однако положение и импульс становятся все более коррелированными по мере развития состояния, потому что части распределения, расположенные дальше от начала координат, требуют большего импульса для достижения: асимптотически,

$W\; ⟶\; 1\; (\pi )\; 3\; ехр\; \; [-\; \alpha \; 2\; (x\; -\; ptm)\; 2].\; \{\backslash \; displaystyle\; W\; \backslash \; longrightarrow\; \{\backslash \; frac\; \{1\}\; \{(\backslash \; pi\; \backslash \; hbar)\; ^\; \{3\}\}\}\; \backslash \; exp\; \backslash \; left\; [-\; \backslash \; alpha\; ^\; \{2\}\; \backslash \; left\; (\backslash \; mathbf\; \{x\}\; -\; \{\backslash \; frac\; \{\; \backslash \; mathbf\; \{p\}\; t\}\; \{m\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; \backslash ,.\}$

(Это относительное "сжатие" отражает распространение свободной волны пакет в координатном пространстве.)

Действительно, можно показать, что кинетическая энергия частицы становится только асимптотически радиальной, в соответствии со стандартным квантово-механическим представлением о ненулевом угловом импульс, определяющий независимость ориентации:

$K\; rad\; =\; \alpha \; 2\; \hslash \; 2\; 2\; m\; (3\; 2\; -\; 1\; 1\; +\; (t\; /\; \tau )\; 2)\; \{\backslash \; displaystyle\; K\; \_\; \{\backslash \; text\; \{rad\}\}\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{2\}\; \backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{3\}\; \{2\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{1+\; (t\; /\; \backslash \; tau)\; ^\; \{2\}\}\}\; \backslash \; справа)\}$

$K\; угл\; =\; \alpha \; 2\; \hslash \; 2\; 2\; м\; 1\; 1\; +\; (t\; /\; \tau )\; 2.\; \{\backslash \; displaystyle\; K\; \_\; \{\backslash \; text\; \{ang\}\}\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{2\}\; \backslash \; hbar\; ^\; \{2\}\}\; \{2m\}\}\; \{\backslash \; frac\; \{1\}\; \{1+\; (t\; /\; \backslash \; tau)\; ^\; \{\; 2\}\}\}\; ~.\}$

Потенциал Морзе

Потенциал Морзе используется для аппроксимации колебательной структуры двухатомной молекулы.

Воспроизвести медиа Функция Вигнера эволюция во времени потенциала Морзе U (x) = 20 (1 - e) в атомных единицах (au). Сплошные линии представляют набор уровней для гамильтониана H (x, p) = p / 2 + U (x).

Квантовое туннелирование

Туннелирование отличительный квантовый эффект, когда квантовая частица, не имея достаточной энергии, чтобы лететь над ней, все же проходит через барьер. Этого эффекта нет в классической механике.

Воспроизвести медиа Функция Вигнера для туннелирования через потенциальный барьер U (x) = 8e в атомных единицах (а.е.). Сплошные линии представляют набор уровней для гамильтониана H (x, p) = p / 2 + U (x).

четвертый потенциал

Play media функция Вигнера эволюция во времени для потенциала U (x) = 0,1x в атомных единицах (а.е.). Сплошные линии представляют набор уровней для гамильтониана H (x, p) = p / 2 + U (x).

Шредингер состояние кошки Функция Вигнера двух интерферирующих когерентных состояний, эволюционирующих через гамильтониан ШО. Соответствующие проекции импульса и координат нанесены справа и под графиком в фазовом пространстве.

Ссылки

1. ^ Groenewold, H.J. (1946). «О принципах элементарной квантовой механики». Physica. 12 (7): 405–460. Bibcode : 1946Phy.... 12..405G. doi : 10.1016 / S0031-8914 (46) 80059-4.
2. ^ Moyal, J. E.; Бартлетт, М. С. (1949). «Квантовая механика как статистическая теория». Математические труды Кембриджского философского общества. 45 (1): 99–124. Bibcode : 1949PCPS... 45... 99M. doi : 10.1017 / S0305004100000487.
3. ^Вейл, Х. (1927). "Quantenmechanik und Gruppentheorie". Zeitschrift für Physik. 46 (1–2): 1–46. Bibcode : 1927ZPhy... 46.... 1W. doi : 10.1007 / BF02055756. S2CID 121036548.
4. ^ Вигнер, Э. (1932). «О квантовой поправке на термодинамическое равновесие». Физический обзор. 40 (5): 749–759. Bibcode : 1932PhRv... 40..749W. doi : 10.1103 / PhysRev.40.749. hdl : 10338.dmlcz / 141466.
5. ^Али, С. Тареке; Энглиш, Мирослав (2005). «Методы квантования: руководство для физиков и аналитиков». Обзоры по математической физике. 17 (4): 391–490. arXiv : math-ph / 0405065. doi : 10.1142 / S0129055X05002376. S2CID 119152724.
6. ^ Curtright, T. L.; Захос, К. К. (2012). «Квантовая механика в фазовом пространстве». Информационный бюллетень по физике Азиатско-Тихоокеанского региона. 01 : 37–46. arXiv : 1104.5269. doi : 10.1142 / S2251158X12000069. S2CID 119230734.
7. ^ C. Захос, Д. Фэрли и Т. Кертрайт, «Квантовая механика в фазовом пространстве» (World Scientific, Сингапур, 2005) ISBN 978-981-238-384-6.
8. ^Коэн, Л. ( 1966 г.). «Обобщенные функции распределения в фазовом пространстве». Журнал математической физики. 7 (5): 781–786. Bibcode : 1966JMP..... 7..781C. doi : 10.1063 / 1.1931206.
9. ^ Agarwal, G.S.; Вольф, Э. (1970). «Исчисление функций от некоммутирующих операторов и общие методы фазового пространства в квантовой механике. II. Квантовая механика в фазовом пространстве». Physical Review D. 2 (10): 2187–2205. Bibcode : 1970PhRvD... 2.2187A. doi : 10.1103 / PhysRevD.2.2187.
10. ^Сударшан, Э.С.Г. (1963). «Эквивалентность квазиклассического и квантово-механического описания статистических световых пучков». Письма с физическим обзором. 10 (7): 277–279. Bibcode : 1963PhRvL..10..277S. doi : 10.1103 / PhysRevLett.10.277.
11. ^Глаубер, Рой Дж. (1963). «Когерентные и некогерентные состояния радиационного поля». Физический обзор. 131 (6): 2766–2788. Bibcode : 1963PhRv..131.2766G. doi : 10.1103 / PhysRev.131.2766.
12. ^Коди Хусими (1940). «Некоторые формальные свойства матрицы плотности», Тр. Phys. Математика. Soc. Jpn. 22 : 264–314.
13. ^Agarwal, G.S.; Вольф, Э. (1970). «Исчисление функций от некоммутирующих операторов и общие методы фазового пространства в квантовой механике. I. Теоремы отображения и порядок функций от некоммутирующих операторов». Physical Review D. 2 (10): 2161–2186. Bibcode : 1970PhRvD... 2.2161A. doi : 10.1103 / PhysRevD.2.2161.
14. ^Кэхилл, К. Э.; Глаубер, Р. Дж. (1969). «Упорядоченные разложения в операторах амплитуды бозона» (PDF). Физический обзор. 177 (5): 1857–1881. Bibcode : 1969PhRv..177.1857C. doi : 10.1103 / PhysRev.177.1857.; Кэхилл, К. Э.; Глаубер, Р. Дж. (1969). «Операторы плотности и распределения квазивероятностей». Физический обзор. 177 (5): 1882–1902. Bibcode : 1969PhRv..177.1882C. doi : 10.1103 / PhysRev.177.1882..
15. ^Лакс, Мелвин (1968). «Квантовый шум. XI. Многократное соответствие между квантовыми и классическими случайными процессами». Физический обзор. 172 (2): 350–361. Bibcode : 1968PhRv..172..350L. doi : 10.1103 / PhysRev.172.350.
16. ^Бейкер, Джордж А. (1958). "Формулировка квантовой механики на основе распределения квази-вероятностей, индуцированного в фазовом пространстве". Физический обзор. 109 (6): 2198–2206. Bibcode : 1958PhRv..109.2198B. doi : 10.1103 / PhysRev.109.2198.
17. ^Фэрли, Д. Б. (1964). «Формулировка квантовой механики в терминах функций фазового пространства». Математические труды Кембриджского философского общества. 60 (3): 581–586. Bibcode : 1964PCPS... 60..581F. doi : 10.1017 / S0305004100038068.
18. ^ Curtright, T.; Fairlie, D.; Захос, К. (1998). «Особенности не зависящих от времени функций Вигнера». Physical Review D. 58 (2): 025002. arXiv : hep-th / 9711183. Bibcode : 1998PhRvD..58b5002C. doi : 10.1103 / PhysRevD.58.025002. S2CID 288935.
19. ^Мехта, К. Л. (1964). "Фазово-пространственная формулировка динамики канонических переменных". Журнал математической физики. 5 (5): 677–686. Bibcode : 1964JMP..... 5..677M. doi : 10.1063 / 1.1704163.
20. ^M. Олива, Д. Какофенгитис и О. Штойернагель (2018). «Ангармонические квантово-механические системы не имеют траекторий в фазовом пространстве». Physica A. 502 : 201–210. arXiv : 1611.03303. Bibcode : 2018PhyA..502..201O. doi : 10.1016 / j.physa.2017.10.047. S2CID 53691877. CS1 maint: несколько имен: список авторов (ссылка )
21. ^Маринов, М.С. (1991). «Новый тип фазового пути интеграл ". Physics Letters A. 153 (1): 5–11. Bibcode : 1991PhLA..153.... 5M. doi : 10.1016 / 0375-9601 (91) 90352-9.
22. ^Криворученко, М.И.; Фесслер, Аманд (2007). «Символы Вейля операторов Гейзенберга канонических координат и импульсов как квантовые характеристики». Математическая физика. 48 (5): 052107. arXiv : Quant-ph / 0604075. Bibcode : 2007JMP....48e2107K. doi : 10.1063 / 1.2735816. S2CID 42068076.
23. ^Curtright, TL Зависящие от времени функции Вигнера
24. ^JP Dahl и WP Schleich, «Концепции радиальной и угловой кинетической энергии», Phys. Rev. A, 65 (2002). doi : 10.1103/PhysRevA.65.022109