Волновой пакет

Короткий «всплеск» или «огибающая» ограниченного волнового воздействия, который распространяется как единое целое Волновой пакет без дисперсии (реальный или мнимая часть) Волновой пакет с дисперсией

В физике волновой пакет (или последовательность волн ) представляет собой короткий «всплеск» или «огибающую. "локализованного волнового воздействия, которое распространяется как единое целое. Волновой пакет может быть проанализирован или может быть синтезирован из бесконечного набора составляющих синусоидальных волн различных волновых чисел, с фазами и амплитудами, так что они конструктивно интерферируют только на небольшом область космоса, и разрушительно в другом месте. Каждая составляющая волновой функции и, следовательно, волновой пакет, являются решениями волнового уравнения. В зависимости от волнового уравнения профиль волнового пакета может оставаться постоянным (нет дисперсии, см. Рисунок) или он может изменяться (дисперсия) во время распространения.

Квантовая механика придает волновому пакету особое значение; он интерпретируется как амплитуда вероятности, его квадрат нормы, описывающий плотность вероятности того, что частица или частицы в определенном состоянии будут измерены, чтобы иметь заданное положение или импульс. Волновое уравнение в данном случае является уравнением Шредингера. Можно вывести временную эволюцию квантово-механической системы, аналогично процессу гамильтониана формализма в классической механике. Дисперсионный характер решений уравнения Шредингера сыграл важную роль в отказе от первоначальной интерпретации Шредингера и принятии правила Борна.

в координатном представлении волны (например, Декартова система координат ), положение вероятности локализации физического объекта определяется положением пакетного решения. Более того, чем уже пространственный волновой пакет и, следовательно, чем лучше локализовано положение волнового пакета, тем больше разброс в импульсе волны. Этот компромисс между спредом позиции и спредом импульса является характерной чертой Heisenberg принципа неопределенности и будет проиллюстрирован ниже.

Содержание

• 1 Историческая справка
• 2 Основные закономерности
  • 2.1 Недисперсия
  • 2.2 Дисперсия
• 3 Гауссовские волновые пакеты в квантовой механике
• 4 Цепочка волн Эйри
• 5 Бесплатный пропагатор
• 6 Аналитическое продолжение распространения
• 7 См. Также
• 8 Примечания
• 9 Примечания
• 10 Ссылки
• 11 Внешние ссылки

Историческая справка

В В начале 1900-х годов стало очевидно, что классическая механика имеет несколько серьезных недостатков. Исаак Ньютон первоначально предложил идею о том, что свет приходит в виде дискретных пакетов, которые он назвал корпускулами, но волнообразное поведение многих световых явлений быстро привело ученых к предпочтению волнового описания электромагнетизм. Только в 1930-х годах природа частиц света стала по-настоящему широко приниматься в физике. Развитие квантовой механики - и ее успех в объяснении запутанных экспериментальных результатов - лежало в основе этого признания. Таким образом, одна из основных концепций в формулировке квантовой механики - это свет, приходящий в виде дискретных пучков, называемых фотонами. Энергия фотона является функцией его частоты,

$E\; =\; h\; \nu .\; \{\backslash \; displaystyle\; E\; =\; h\; \backslash \; nu.\}$

Энергия фотона равна постоянной Планка, h, умноженной на его частоту, ν. Это разрешило проблему в классической физике, названную ультрафиолетовой катастрофой.

. Идеи квантовой механики продолжали развиваться на протяжении всего 20 века. Созданная картина представляла собой мир из частиц, в котором все явления и материя состоят из отдельных частиц и взаимодействуют с ними; однако эти частицы описывались волной вероятности. Взаимодействия, местоположения и вся физика были бы сведены к вычислениям этих амплитуд вероятности.

Подобная частицам природа мира была подтверждена экспериментами более века, в то время как волновые явления могут быть охарактеризованы как следствия волнового пакета квантовых частиц (см. волна-частица двойственность ). Согласно принципу дополнительности, волнообразные и частичные характеристики никогда не проявляются одновременно, то есть в одном эксперименте; см., однако, эксперимент Афшара и оживленную дискуссию вокруг него.

Основные поведения

Плотность пространственной вероятности изначально гауссовского состояния, захваченного в бесконечной потенциальной яме, испытывающей периодическое квантовое туннелирование в центрированной потенциальной стенке.

Недисперсионный

Как В качестве примера распространения без дисперсии рассмотрим волновые решения следующего волнового уравнения из классической физики

$\partial \; 2\; u\; \partial \; t\; 2\; =\; c\; 2\; \nabla \; 2\; u,\; \{\backslash \; displaystyle\; \{\backslash \; partial\; ^\; \{\; 2\}\; u\; \backslash \; over\; \backslash \; partial\; t\; ^\; \{2\}\}\; =\; c\; ^\; \{2\}\; \{\backslash \; nabla\; ^\; \{2\}\; u\},\}$

где c - скорость распространения волны в данной среде.

Используя соглашение физики о времени, exp (−iωt), волновое уравнение имеет плоско-волновые решения

$u\; (x,\; t)\; =\; ei\; (k\; \cdot \; x\; -\; \omega \; t),\; \{\backslash \; displaystyle\; u\; (\backslash \; mathbf\; \{x\},\; t)\; =\; e\; ^\; \{i\; \{(\backslash \; mathbf\; \{k\; \backslash \; cdot\; x\}\}\; -\; \backslash \; omega\; t)\},\}$

где

$\omega \; 2\; =\; |\; k\; |\; 2\; c\; 2\; \{\backslash \; displaystyle\; \backslash \; omega\; ^\; \{2\}\; =\; |\; \backslash \; mathbf\; \{k\}\; |\; ^\; \{2\}\; c\; ^\; \{2\}\}$и $|\; k\; |\; 2\; знак\; равно\; К\; Икс\; 2\; +\; К\; Y\; 2\; +\; К\; Z\; 2.\; \{\backslash \; displaystyle\; |\; \backslash \; mathbf\; \{k\}\; |\; ^\; \{2\}\; =\; k\_\; \{x\}\; ^\; \{2\}\; +\; k\_\; \{y\}\; ^\; \{2\}\; +\; k\_\; \{z\}\; ^\; \{2\}.\}$

Это соотношение между ω и k должны быть действительными, чтобы плоская волна была решением волнового уравнения. Это называется дисперсионным соотношением .

Для упрощения рассмотрим только волны, распространяющиеся в одном измерении (расширение до трех измерений не вызывает затруднений). Тогда общее решение:

$u\; (x,\; t)\; =\; A\; ei\; (kx\; -\; \omega \; t)\; +\; B\; e\; -\; i\; (kx\; +\; \omega \; t),\; \{\backslash \; displaystyle\; u\; (x,\; t)\; =\; Ae\; ^\; \{i\; (\; kx-\; \backslash \; omega\; t)\}\; +\; Be\; ^\; \{-\; i\; (kx\; +\; \backslash \; omega\; t)\},\}$

в котором мы можем взять ω = kc. Первый член представляет волну, распространяющуюся в положительном направлении оси x, поскольку она является функцией только x - ct; второй член, являющийся функцией x + ct, представляет волну, распространяющуюся в отрицательном направлении x.

Волновой пакет - это локализованное возмущение, которое возникает в результате суммы множества различных волновых форм. Если пакет сильно локализован, необходимо больше частот, чтобы обеспечить конструктивную суперпозицию в области локализации и деструктивную суперпозицию за пределами области. Исходя из основных решений в одном измерении, общий вид волнового пакета может быть выражен как

$u\; (x,\; t)\; =\; 1\; 2\; \pi \; \int \; -\; \infty \; \infty \; A\; (k)\; ei\; (kx\; -\; \omega \; (k)\; t)\; dk.\; \{\backslash \; displaystyle\; u\; (x,\; t)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash ,\; \backslash \; infty\}\; A\; (k)\; ~\; e\; ^\; \{i\; (kx-\; \backslash \; omega\; (k)\; t)\}\; dk.\}$

Как и в случае плоской волны, волновой пакет движется вправо при ω (k) = kc, поскольку u (x, t) = F (x - ct) и слева при ω (k) = −kc, поскольку u (x, t) = F (x + ct).

Коэффициент ⁄ √2π исходит из соглашений преобразования Фурье. Амплитуда A (k) содержит коэффициенты линейной суперпозиции плоских волновых решений. Эти коэффициенты, в свою очередь, могут быть выражены как функция от u (x, t), вычисленная при t = 0 путем обращения приведенного выше соотношения преобразования Фурье:

$A\; (k)\; =\; 1\; 2\; \pi \; \int \; -\; \infty \; \infty \; u\; (x,\; 0)\; е\; -\; ikxdx.\; \{\backslash \; Displaystyle\; A\; (k)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash ,\; \backslash \; infty\}\; u\; (x,\; 0)\; ~\; e\; ^\; \{-\; ikx\}\; dx.\}$

Например, если выбрать

$u\; (x,\; 0)\; =\; e\; -\; x\; 2\; +\; ik\; 0\; x,\; \{\backslash \; displaystyle\; u\; (x,\; 0)\; =\; e\; ^\; \{-\; x\; ^\; \{2\}\; +\; ik\_\; \{0\}\; x\},\}$

получаем

$A\; (k)\; =\; 1\; 2\; e\; -\; (k\; -\; k\; 0)\; 2\; 4,\; \{\backslash \; displaystyle\; A\; (k)\; =\; \{\backslash \; frac\; \{1\}\; \{\; \backslash \; sqrt\; \{2\}\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{(k-k\_\; \{0\})\; ^\; \{2\}\}\; \{4\}\}\},\}$

и, наконец,

$u\; (x,\; t)\; =\; е\; -\; (x\; -\; ct)\; 2\; +\; ik\; 0\; (x\; -\; ct)\; =\; e\; -\; (x\; -\; ct)\; 2\; [cos\; \; (2\; \pi \; x\; -\; ct\; \lambda )\; +\; i\; sin\; \; (2\; \pi \; x\; -\; ct\; \lambda )].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; u\; (x,\; t)\; =\; e\; ^\; \{-\; (x-ct)\; ^\; \{2\}\; +\; ik\_\; \{0\}\; (x-ct)\}\; \backslash \backslash \; =\; e\; ^\; \{-\; (\; x-ct)\; ^\; \{2\}\}\; \backslash \; left\; [\backslash \; cos\; \backslash \; left\; (2\; \backslash \; pi\; \{\backslash \; frac\; \{x-ct\}\; \{\backslash \; lambda\}\}\; \backslash \; right)\; +\; i\; \backslash \; sin\; \backslash \; left\; (2\; \backslash \; pi\; \{\backslash \; frac\; \{\; x-ct\}\; \{\backslash \; lambda\}\}\; \backslash \; right)\; \backslash \; right].\; \backslash \; end\; \{align\}\}\}$

Недисперсное распространение действительной или мнимой части этого волнового пакета показано на приведенной выше анимации.

.

Дисперсионный

Плотность вероятности в пространстве координат первоначально гауссовского состояния, движущегося в одном измерении с минимально неопределенным постоянным импульсом в свободном пространстве.

Напротив, в качестве примера распространения теперь с дисперсией рассмотрим вместо этого решения Уравнение Шредингера (Pauli 2000, где m и ħ равны единице),

$i\; \partial \; \psi \; \partial \; t\; =\; -\; 1\; 2\; \nabla \; 2\; \psi ,\; \{\backslash \; displaystyle\; i\; \{\backslash \; partial\; \backslash \; psi\; \backslash \; over\; \backslash \; partial\; t\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; nabla\; ^\; \{2\}\; \backslash \; psi\},\}$

, что дает дисперсионное соотношение

$\omega \; =\; 1\; 2\; |\; k\; |\; 2.\; \{\backslash \; displaystyle\; \backslash \; omega\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; |\; \backslash \; mathbf\; \{k\}\; |\; ^\; \{2\}.\}$

Еще раз, ограничивая внимание одним измерением, решение уравнения Шредингера, удовлетворяющее начальному условие $\psi \; (x,\; 0)\; =\; 2\; /\; \pi \; 4\; exp\; \; (-\; x\; 2\; +\; ik\; 0\; x)\; \{\backslash \; displaystyle\; ~\; \backslash \; psi\; (x,\; 0)\; =\; \{\backslash \; sqrt\; [\{4\}]\; \{2\; /\; \backslash \; pi\}\}\; \backslash \; exp\; (\{-\; x\; ^\; \{2\}\; +\; ik\_\; \{0\}\; x\})\}$, представляющий волновой пакет, локализованный в пространстве в начале координат, рассматривается как

$\psi \; (x,\; t)\; =\; 2\; /\; \pi \; 4\; 1\; +\; 2\; ite\; -\; 1\; 4\; k\; 0\; 2\; e\; -\; 1\; 1\; +\; 2\; it\; (x\; -\; ik\; 0\; 2)\; 2\; =\; 2\; /\; \pi \; 4\; 1\; +\; 2\; ite\; -\; 1\; 1\; +\; 4\; t\; 2\; (\; x\; -\; k\; 0\; t)\; 2\; ei\; 1\; 1\; +\; 4\; t\; 2\; ((k\; 0\; +\; 2\; tx)\; x\; -\; 1\; 2\; tk\; 0\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; psi\; (x,\; t)\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; [\{4\}]\; \{2\; /\; \backslash \; pi\}\}\; \{\backslash \; sqrt\; \{1\; +\; 2it\}\}\}\; e\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; k\_\; \{0\}\; ^\; \{2\}\}\; ~\; e\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{1\; +\; 2it\}\}\; \backslash \; left\; (x\; -\; \{\backslash \; frac\; \{ik\_\; \{0\}\})\; \{2\}\}\; \backslash \; right)\; ^\; \{2\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; [\{4\}]\; \{2\; /\; \backslash \; pi\}\}\; \{\backslash \; sqrt\; \{1\; +\; 2it\}\}\}\; e\; ^\; \{-\; \{\backslash \; гидроразрыв\; \{1\}\; \{1\; +\; 4t\; ^\; \{2\}\}\}\; (x-k\_\; \{0\}\; t)\; ^\; \{2\}\}\; ~\; e\; ^\; \{i\; \{\backslash \; frac\; \{1\}\; \{1\; +\; 4t\; ^\; \{2\}\}\}\; \backslash \; left\; ((k\_\; \{0\}\; +\; 2tx)\; x\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; tk\_\; \{0\}\; ^\; \{2\}\; \backslash \; right)\}\; ~.\; \backslash \; end\; \{align\}\}\}$

Впечатление от дисперсионное поведение этого волнового пакета получается путем рассмотрения плотности вероятности:

$|\; \psi \; (x,\; t)\; |\; 2\; знак\; равно\; 2\; /\; \pi \; 1\; +\; 4\; т\; 2\; е\; -\; 2\; (х\; -\; к\; 0\; т)\; 2\; 1\; +\; 4\; т\; 2.\; \{\backslash \; displaystyle\; |\; \backslash \; psi\; (x,\; t)\; |\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{2\; /\; \backslash \; pi\}\}\; \{\backslash \; sqrt\; \{1\; +\; 4t\; ^\; \{2\}\}\}\}\; ~\; e\; ^\; \{-\; \{\; \backslash \; frac\; \{2\; (x-k\_\; \{0\}\; t)\; ^\; \{2\}\}\; \{1\; +\; 4t\; ^\; \{2\}\}\}\}\; ~.\}$

Очевидно, что этот дисперсионный волновой пакет, двигаясь с постоянной групповая скорость koбыстро делокализуется: ее ширина увеличивается со временем как √ 1 + 4t² → 2t, поэтому в конечном итоге она распространяется в неограниченную область пространства.

профиль импульса A (k) остается неизменным. ток вероятности равен

$j\; =\; \rho \; v\; =\; 1\; 2\; i\; (\psi \; \ast \; \nabla \; \psi \; -\; \psi \; \nabla \; \psi \; \ast )\; =\; \rho \; (k\; 0\; +\; 4\; t\; (x\; -\; k\; 0\; t)\; 1\; +\; 4\; т\; 2).\; \{\backslash \; displaystyle\; j\; =\; \backslash \; rho\; v\; =\; \{\backslash \; frac\; \{1\}\; \{2i\}\}\; (\backslash \; psi\; ^\; \{*\}\; \backslash \; nabla\; \backslash \; psi\; -\; \backslash \; psi\; \backslash \; nabla\; \backslash \; psi\; ^\; \{*\})\; =\; \backslash \; rho\; \backslash \; left\; (k\_\; \{\; 0\}\; +\; \{\backslash \; frac\; \{4t\; (x-k\_\; \{0\}\; t)\}\; \{1\; +\; 4t\; ^\; \{2\}\}\}\; \backslash \; right).\}$

Гауссовские волновые пакеты в квантовой механике

Суперпозиция одномерных плоских волн (синий), которые в сумме образуют квантовый гауссов волновой пакет (красный), который распространяется вправо при расширении. Синие точки следуют за фазовой скоростью каждой плоской волны, а красная линия - за центральной групповой скоростью. Плотность пространственной вероятности изначально гауссовского состояния, заключенного в бесконечную потенциальную яму, испытывающую периодическое квантовое туннелирование в центрированной потенциальной стенке. 1D Гауссовский волновой пакет, показанный в комплексной плоскости, для a = 2 и k = 4

Вышеупомянутый дисперсионный гауссовский волновой пакет, ненормализованный и просто центрированный в начале координат, вместо этого, при t = 0, теперь может быть записан в 3D, теперь в стандартных единицах:

$\psi \; (r,\; 0)\; =\; e\; -\; r\; \cdot \; r\; /\; 2\; a,\; \{\backslash \; displaystyle\; \backslash \; psi\; (\backslash \; mathbf\; \{r\},\; 0)\; =\; e\; ^\; \{-\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\; /\; 2a\},\}$

где a - положительное действительное число, квадрат ширины волнового пакета,

$a\; =\; 2\; ⟨r\; \cdot \; r⟩\; /\; 3\; ⟨1⟩\; =\; 2\; (\; \Delta \; x)\; 2.\; \{\backslash \; displaystyle\; a\; =\; 2\; \backslash \; langle\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\; \backslash \; rangle\; /\; 3\; \backslash \; langle\; 1\; \backslash \; rangle\; =\; 2\; (\backslash \; Delta\; x)\; ^\; \{2\}.\}$

Преобразование Фурье также гауссовский в терминах волнового числа, t = 0, k -вектора, (с обратной шириной,

$1\; /\; a\; =\; 2\; ⟨k\; \cdot \; k⟩\; /\; 3\; ⟨1⟩\; =\; 2\; (\Delta \; px\; /\; \hslash )\; 2,\; \{\backslash \; displaystyle\; 1\; /\; a\; =\; 2\; \backslash \; langle\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\}\; \backslash \; rangle\; /\; 3\; \backslash \; langle\; 1\; \backslash \; rangle\; =\; 2\; (\backslash \; Delta\; p\_\; \{x\}\; /\; \backslash \; hbar)\; ^\; \{2\},\}$

так, чтобы

$\Delta \; x\; \Delta \; px\; =\; \hslash \; /\; 2,\; \{\backslash \; displaystyle\; \backslash \; Delta\; x\; \backslash \; Delta\; p\_\; \{x\}\; =\; \backslash \; hbar\; /\; 2,\}$

, т. Е. Насыщает соотношение неопределенности ),

$\psi \; (k,\; 0)\; =\; (2\; \pi \; a)\; 3/2\; e\; -\; ak\; \cdot \; k\; /\; 2.\; \{\backslash \; displaystyle\; \backslash \; psi\; (\backslash \; mathbf\; \{k\},\; 0)\; =\; (2\; \backslash \; pi\; a)\; ^\; \{3/2\}\; e\; ^\; \{-\; a\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\}\; /\; 2\}.\}$

Каждая отдельная волна вращается только по фазе во времени, так что зависящее от времени решение с преобразованием Фурье имеет вид

$\Psi \; (k,\; t)\; =\; (2\; \pi \; a)\; 3/2\; e\; -\; ak\; \cdot \; k\; /\; 2\; e\; -\; i\; E\; t\; /\; \hslash \; =\; (2\; \pi \; a)\; 3/2\; e\; -\; ak\; \cdot \; k\; /\; 2\; -\; i\; (\hslash \; 2\; k\; \cdot \; k\; /\; 2\; m)\; t\; /\; \hslash \; =\; (2\; \pi \; a)\; 3/2\; e\; -\; (a\; +\; i\; \hslash \; т\; /\; м)\; к\; \cdot \; к\; /\; 2.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Psi\; (\backslash \; mathbf\; \{k\},\; t)\; =\; (2\; \backslash \; pi\; a)\; ^\; \{3/2\}\; e\; ^\; \{-\; a\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\; \}\; /\; 2\}\; e\; ^\; \{-\; iEt\; /\; \backslash \; hbar\}\; \backslash \backslash \; =\; (2\; \backslash \; pi\; a)\; ^\; \{3/2\}\; e\; ^\; \{-\; a\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\}\; /\; 2-i\; (\backslash \; hbar\; ^\; \{2\}\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\}\; /\; 2m)\; t\; /\; \backslash \; hbar\}\; \backslash \backslash \; =\; (2\; \backslash \; pi\; a)\; ^\; \{3/2\}\; e\; ^\; \{-\; (a\; +\; i\; \backslash \; hbar\; t\; /\; m)\; \backslash \; mathbf\; \{k\}\; \backslash \; cdot\; \backslash \; mathbf\; \{k\}\; /2\}.\backslash end\{aligned\}\}\}$

Обратное преобразование Фурье по-прежнему гауссово, но теперь параметр a стал сложным, и существует общий коэффициент нормализации.

$\Psi \; (r,\; t)\; =\; (aa\; +\; i\; \hslash \; t\; /\; m)\; 3/2\; e\; -\; r\; \cdot \; r\; 2\; (a\; +\; i\; \hslash \; t\; /\; m).\; \{\backslash \; Displaystyle\; \backslash \; Psi\; (\backslash \; mathbf\; \{r\},\; t)\; =\; \backslash \; left\; (\{a\; \backslash \; over\; a\; +\; i\; \backslash \; hbar\; t\; /\; m\}\; \backslash \; right)\; ^\; \{3/2\}\; e\; ^\; \{-\; \{\backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\; \backslash \; over\; 2\; (a\; +\; i\; \backslash \; hbar\; t\; /\; m)\}\}.\}$

Интеграл от по всему пространству инвариантен, потому что это скалярное произведение с нулевым состоянием энергия, которая представляет собой волну с бесконечной длиной волны, постоянную функцию пространства. Для любого собственного состояния энергии η (x) внутренний продукт,

$⟨\eta \; |\; \psi ⟩\; знак\; равно\; \int \; \eta \; (р)\; \psi \; (г)\; d\; 3\; р,\; \{\backslash \; Displaystyle\; \backslash \; langle\; \backslash \; eta\; |\; \backslash \; psi\; \backslash \; rangle\; =\; \backslash \; int\; \backslash \; eta\; (\backslash \; mathbf\; \{r\})\; \backslash \; psi\; (\backslash \; mathbf\; \{r\})\; d\; ^\; \{3\}\; \backslash \; mathbf\; \{r\},\}$

изменяется только во времени простым способом: его фаза вращается с частотой, определяемой энергией η. Когда η имеет нулевую энергию, как волна с бесконечной длиной волны, она вообще не меняется.

Интеграл ∫ | Ψ | dr также инвариантен, что является утверждением сохранения вероятности. Явно

$P\; (r)\; =\; |\; \Psi \; |\; 2\; знак\; равно\; \Psi \; \ast \; \Psi \; знак\; равно\; (aa\; 2\; +\; (\hslash \; t\; /\; m)\; 2)\; 3\; e\; -\; ar\; \cdot \; ra\; 2\; +\; (\hslash \; t\; /\; m)\; 2,\; \{\backslash \; displaystyle\; P\; (r)\; =\; |\; \backslash \; Psi\; |\; ^\; \{2\}\; =\; \backslash \; Psi\; ^\; \{*\}\; \backslash \; Psi\; =\; \backslash \; left\; (\{a\; \backslash \; over\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; (\backslash \; hbar\; t\; /\; m)\; ^\; \{2\}\}\}\}\; \backslash \; right)\; ^\; \{3\}\; ~\; e\; ^\; \{-\; \{a\; \backslash ,\; \backslash \; mathbf\; \{r\}\; \backslash \; cdot\; \backslash \; mathbf\; \{r\}\; \backslash \; над\; ^\; \{2\}\; +\; (\backslash \; hbar\; t\; /\; m)\; ^\; \{2\}\}\},\}$

в котором √a ширина P (r) при t = 0; r - расстояние от начала координат; скорость частицы равна нулю; а начало отсчета времени t = 0 можно выбрать произвольно.

Ширина гауссианы - это интересная величина, которую можно определить по плотности вероятности, | Ψ |,

$a\; 2\; +\; (\hslash \; t\; /\; m)\; 2\; a.\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{a\; ^\; \{2\}\; +\; (\backslash \; hbar\; t\; /\; m)\; ^\; \{2\}\; \backslash \; over\; a\}\}.\}$

Эта ширина со временем растет линейно, как ħt / (m√a), указывающий на расширение волнового пакета .

Например, если волновой пакет электрона изначально локализован в области с атомными размерами (то есть 10 м), то ширина пакета удваивается примерно за 10 с. Ясно, что волновые пакеты частиц действительно распространяются очень быстро (в свободном пространстве): например, через 1 мс ширина вырастет примерно до километра.

Этот линейный рост является отражением (неизменной во времени) неопределенности импульса: волновой пакет ограничен узким Δx = √a / 2 и поэтому имеет неопределенный импульс (согласно принцип неопределенности ) на величину / √2a, разброс скорости ħ / m√2a, и, таким образом, в будущем положении на ħt / m√2a. Тогда соотношение неопределенностей представляет собой строгое неравенство, действительно очень далекое от насыщения! Начальная неопределенность ΔxΔp = ħ / 2 теперь увеличилась в t / ma (для больших t).

Цепочка волн Эйри

В отличие от вышеупомянутого гауссовского волнового пакета, было замечено, что конкретная волновая функция, основанная на функциях Эйри, распространяется свободно без дисперсии огибающей., сохраняя свою форму. Он ускоряется без искажений в отсутствие силового поля: ψ = Ai (B (x − B³t ²)) exp (iB³t (x − 2B³t² / 3)). (Для простоты ħ = 1, m = 1/2, а B - константа, ср. обезразмеривание.)

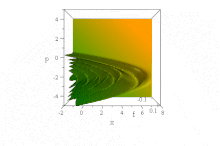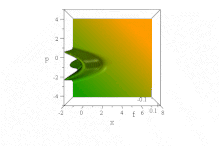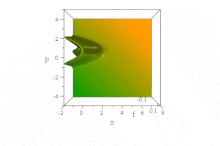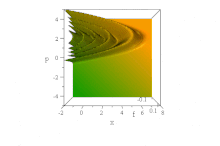Усеченный вид развития во времени фронта Эйри в фазовом пространстве. (Щелкните, чтобы оживить.)

Тем не менее, нет никакого диссонанса с теоремой Эренфеста в этой бессиловой ситуации, потому что состояние одновременно ненормализуемо и имеет неопределенное (бесконечное) ⟨x⟩ для все время. (Насколько это можно определить, ⟨p⟩ = 0 для всех времен, несмотря на кажущееся ускорение фронта.)

В фазовом пространстве это очевидно в чистое состояние Распределение квазивероятностей Вигнера этого волнового потока, форма которого по x и p неизменна с течением времени, но характеристики которого ускоряются вправо, в ускоряющихся параболах B (x − B³t ²) + (p / B - tB²) ² = 0,

$W\; (x,\; p;\; t)\; =\; W\; (x\; -\; B\; 3\; t\; 2,\; p\; -\; B\; 3\; t;\; 0)\; =\; 1\; 2\; 1/3\; \pi \; BA\; i\; (2\; 2/3\; (B\; x\; +\; p\; 2\; B\; 2\; -\; 2\; B\; pt)).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; W\; (x,\; p;\; t)\; =\; W\; (xB\; ^\; \{3\}\; t\; ^\; \{2\},\; pB\; ^\; \{3\}\; t;\; 0)\; \backslash \backslash \; =\; \{1\; \backslash \; over\; 2\; ^\; \{1/3\}\; \backslash \; pi\; B\}\; ~\; \backslash \; mathrm\; \{Ai\}\; \backslash \; left\; (2\; ^\; \{2/3\}\; \backslash \; left\; (Bx\; +\; \{p\; ^\; \{2\}\; \backslash \; over\; B\; ^\; \{2\}\}\; -\; 2Bpt\; \backslash \; right)\; \backslash \; справа).\; \backslash \; end\; \{align\}\}\}$

Обратите внимание, что распределение импульса, полученное интегрированием по всем x, является постоянным. Поскольку это плотность вероятности в импульсном пространстве, очевидно, что сама волновая функция не нормируема.

В 2018 году первое экспериментальное наблюдение кубической фазы ускоряющихся волновых пакетов Эйри было достигнуто при сотрудничестве исследователей из израильских, немецких и американских университетов.

Бесплатный пропагатор

Предел узкой ширины обсуждаемого решения для гауссовского волнового пакета - это свободное ядро ​​пропагатора K. Для других дифференциальных уравнений это обычно называется функцией Грина, но в квантовой механике принято зарезервировать название функции Грина для временного преобразования Фурье K.

Возвращаясь к одному измерению для простоты, с m и ħ установить равным единице, когда a - бесконечно малая величина ε, начальное условие Гаусса, масштабируемое так, чтобы его интеграл равнялся единице,

$\psi \; 0\; (x)\; =\; 1\; 2\; \pi \; ϵ\; e\; -\; x\; 2\; 2\; ϵ\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{0\}\; (x)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; epsilon\}\}\}\; e\; ^\; \{-\; \{x\; ^\; \{2\}\; \backslash \; over\; 2\; \backslash \; epsilon\}\}\; \backslash ,\}$

становится дельта-функция, δ (x), так что ее эволюция во времени,

$K\; t\; (x)\; =\; 1\; 2\; \pi \; (it\; +\; ϵ)\; e\; -\; x\; 2\; 2\; it\; +\; ϵ\; \{\backslash \; displaystyle\; K\_\; \{\; t\}\; (x)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; (it\; +\; \backslash \; epsilon)\}\}\}\; e\; ^\; \{-\; x\; ^\; \{2\}\; \backslash \; over\; 2it\; +\; \backslash \; epsilon\}\; \backslash ,\}$

дает пропагатор.

Обратите внимание, что очень узкий начальный волновой пакет мгновенно становится бесконечно широким, но с фазой, которая более быстро колеблется при больших значениях x. Это может показаться странным - решение переходит от локализации в одной точке к тому, чтобы быть «везде» во все более поздние времена, но это отражение огромной неопределенности импульса локализованной частицы, как объяснялось выше.

Далее обратите внимание, что норма волновой функции бесконечна, что также верно, поскольку квадрат дельта-функции расходится таким же образом.

Фактор, включающий ε, является бесконечно малой величиной, которая нужна, чтобы гарантировать, что интегралы по K правильно определены. В пределе ε → 0 K становится чисто осциллирующим, и интегралы от K не сходятся абсолютно. В оставшейся части этого раздела он будет установлен в ноль, но для того, чтобы все интегрирования по промежуточным состояниям были четко определены, предел ε → 0 должен приниматься только после вычисления конечного состояния.

Пропагатор - это амплитуда для достижения точки x в момент времени t, когда начинается начало координат, x = 0. Благодаря инвариантности сдвига амплитуда для достижения точки x при запуске в точке y является той же функцией, только теперь переведенной,

$K\; t\; (x,\; y)\; =\; K\; t\; (x\; -\; y)\; =\; 1\; 2\; \pi \; itei\; (x\; -\; у)\; 2\; 2\; т.\; \{\backslash \; displaystyle\; K\_\; \{t\}\; (x,\; y)\; =\; K\_\; \{t\}\; (xy)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; it\}\}\}\; e\; ^\; \{i\; (xy)\; ^\; \{2\}\; \backslash \; over\; 2t\; \}\; \backslash ,.\}$

В пределе, когда t мало, пропагатор, конечно, переходит в дельта-функцию,

$lim\; t\; \to \; 0\; K\; t\; (x\; -\; y)\; =\; \delta \; (x\; -\; y),\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{t\; \backslash \; rightarrow\; 0\}\; K\_\; \{t\}\; (xy)\; =\; \backslash \; delta\; (xy)\; ~,\}$

, но только в смысле распределений : интеграл от этой величины умноженное на произвольную дифференцируемую тестовую функцию дает нулевое значение тестовой функции.

Чтобы увидеть это, обратите внимание, что интеграл по всему пространству K всегда равен 1,

$\int \; K\; t\; (x)\; dx\; =\; 1,\; \{\backslash \; displaystyle\; \backslash \; int\; K\_\; \{t\}\; (x)\; dx\; =\; 1\; \backslash ,,\}$

, поскольку этот интеграл является скалярным произведением K с однородной волновой функцией. Но фазовый множитель в показателе экспоненты имеет ненулевую пространственную производную везде, кроме начала координат, и поэтому, когда время мало, есть быстрые сокращения фазы во всех точках, кроме одной. Это строго верно, когда предел ε → 0 берется в самом конце.

Таким образом, ядро ​​распространения - это (будущая) эволюция дельта-функции во времени, и она в некотором смысле непрерывна: на малых временах оно переходит к начальной дельта-функции. Если исходная волновая функция представляет собой бесконечно узкий пик в позиции y,

$\psi \; 0\; (x)\; =\; \delta \; (x\; -\; y),\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{0\}\; (x)\; =\; \backslash \; delta\; (xy)\; \backslash ,,\}$

становится колебательной волной,

$\psi \; t\; (x)\; =\; 1\; 2\; \pi \; itei\; (x\; -\; y)\; 2/2\; t.\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{t\}\; (x)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; it\}\}\}\; e\; ^\; \{i\; (xy)\; ^\; \{2\}\; /\; 2t\}\; \backslash ,.\}$

Теперь, поскольку каждая функция может быть записана в виде взвешенной суммы таких узких пиков,

$\psi \; 0\; (x)\; =\; \int \; \psi \; 0\; (y)\; \delta \; (x\; -\; y)\; dy,\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{0\}\; (x)\; =\; \backslash \; int\; \backslash \; psi\; \_\; \{0\}\; (y)\; \backslash \; delta\; (xy)\; dy\; \backslash ,,\}$

эволюция во времени каждой функции ψ 0 определяется этим ядром распространения K,

$\psi \; t\; (x)\; =\; \int \; \psi \; 0\; (y)\; 1\; 2\; \pi \; itei\; (x\; -\; y)\; 2/2\; tdy.\; \{\backslash \; Displaystyle\; \backslash \; psi\; \_\; \{t\}\; (x)\; =\; \backslash \; int\; \backslash \; psi\; \_\; \{0\}\; (y)\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; it\}\}\}\; e\; ^\; \{i\; (xy)\; ^\; \{2\}\; /\; 2t\}\; dy\; \backslash ,.\}$

Таким образом, это формальный способ выразить фундаментальное решение или общее решение . Интерпретация этого выражения заключается в том, что амплитуда частицы, которая должна быть найдена в точке x в момент времени t, равна амплитуде, с которой она началась в y, умноженная на амплитуду, которую она перешла от y к x, суммированная по всем возможным начальным точкам. Другими словами, это свертка ядра K с произвольным начальным условием ψ 0,

$\psi \; t\; =\; K\; \ast \; \psi \; 0.\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{t\}\; =\; K\; *\; \backslash \; psi\; \_\; \{0\}\; \backslash ,.\}$

Так как амплитуду прохождения от x до y за время t + t 'можно рассматривать в два этапа, пропагатор подчиняется тождеству композиции,

$\int \; K\; (x\; -\; y;\; t)\; K\; (y\; -\; z;\; t\; \prime )\; dy\; =\; K\; (x\; -\; z;\; t\; +\; t\; \prime ),\; \{\backslash \; displaystyle\; \backslash \; int\; K\; (xy;\; t)\; K\; (yz;\; t\; \text{'})\; dy\; =\; K\; (xz;\; t\; +\; t\text{'})\; ~,\}$

что можно интерпретировать следующим образом: амплитуда, которая проходит от x до z за время t + t ', представляет собой сумму амплитуда, чтобы пройти от x до y за время t, умноженная на амплитуду, чтобы пройти от y до z за время t ', просуммированная по всем возможным промежуточным состояниям y. Это свойство произвольной квантовой системы, и за счет разделения времени на множество сегментов оно позволяет выразить временную эволюцию как интеграл по путям.

Аналитическое продолжение к диффузии

Распространение волновые пакеты в квантовой механике напрямую связаны с распределением плотностей вероятностей в диффузии. Для частицы, которая случайно проходит, функция плотности вероятности в любой точке удовлетворяет уравнению диффузии (также см. уравнение теплопроводности ),

$\partial \; \partial \; T\; \rho \; знак\; равно\; 1\; 2\; \partial \; 2\; \partial \; Икс\; 2\; \rho ,\; \{\backslash \; Displaystyle\; \{\backslash \; partial\; \backslash \; over\; \backslash \; partial\; t\}\; \backslash \; rho\; =\; \{1\; \backslash \; over\; 2\}\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; over\; \backslash \; partial\; x\; ^\; \{2\}\}\; \backslash \; rho\; ~,\}$

где множитель 2, который может быть удален путем изменения масштаба времени или пространства, используется только для удобства.

Решением этого уравнения является гауссово расширение,

$\rho \; t\; (x)\; =\; 1\; 2\; \pi \; te\; -\; x\; 2\; 2\; t,\; \{\backslash \; displaystyle\; \backslash \; rho\; \_\; \{t\}\; (x)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; t\}\}\}\; e\; ^\; \{-\; x\; ^\; \{2\}\; \backslash \; over\; 2t\}\; ~,\}$

и, поскольку интеграл от ρ t постоянен, а ширина сужается в короткие промежутки времени, эта функция приближается к дельта-функции при t = 0,

$lim\; t\; \to \; 0\; \rho \; t\; (x)\; =\; \delta \; (x)\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{t\; \backslash \; rightarrow\; 0\}\; \backslash \; rho\; \_\; \{t\}\; (x)\; =\; \backslash \; delta\; (x)\; \backslash ,\}$

снова только в смысле распределений, так что

$lim\; t\; \to \; 0\; \int \; xf\; (x)\; \rho \; t\; (x)\; =\; f\; (0)\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{t\; \backslash \; rightarrow\; 0\}\; \backslash \; int\; \_\; \{x\}\; f\; (x)\; \backslash \; rho\; \_\; \{t\}\; (x)\; =\; f\; (0)\; \backslash ,\}$

для любого гладкого теста функция f.

Гауссово расширение является ядром распространения для уравнения диффузии и подчиняется тождеству свертки,

$K\; t\; +\; t\; \prime \; =\; K\; t\; \ast \; K\; t\; \prime ,\; \{\backslash \; displaystyle\; K\_\; \{t\; +\; t\; \text{'}\}\; =\; K\_\; \{t\}\; *\; K\_\; \{t\text{'}\}\; \backslash ,,\}$

, что позволяет выразить диффузию как интеграл по путям. Пропагатор - это экспонента оператора H,

$K\; t\; (x)\; =\; e\; -\; t\; H,\; \{\backslash \; displaystyle\; K\_\; \{t\}\; (x)\; =\; e\; ^\; \{-\; tH\}\; \backslash ,,\}$

, который равен оператор инфинитезимальной диффузии,

$H\; =\; -\; \nabla \; 2\; 2.\; \{\backslash \; displaystyle\; H\; =\; -\; \{\backslash \; nabla\; ^\; \{2\}\; \backslash \; over\; 2\}\; \backslash ,.\}$

Матрица имеет два индекса, которые в непрерывном пространстве делают ее функцией x и x '. В этом случае, из-за инвариантности перевода, матричный элемент K зависит только от разницы положения, и удобное злоупотребление обозначениями состоит в том, чтобы ссылаться на оператор, матричные элементы и функцию разности с тем же именем:

$К\; t\; (x,\; x\; \prime )\; =\; K\; t\; (x\; -\; x\; \prime ).\; \{\backslash \; displaystyle\; K\_\; \{t\}\; (x,\; x\; \text{'})\; =\; K\_\; \{t\}\; (x-x\text{'})\; \backslash ,.\}$

Трансляционная инвариантность означает, что непрерывное умножение матриц,

$C\; (x,\; x\; ″)\; =\; \int \; Икс\; \text{'}А\; (Икс,\; Икс\text{'})\; В\; (Икс\; \text{'},\; Икс\; ″),\; \{\backslash \; Displaystyle\; С\; (х,\; х\text{'}\; \text{'})\; =\; \backslash \; int\; \_\; \{х\text{'}\}\; А\; (х,\; х\; \text{'})\; В\; (х\text{'},\; x\; \text{'}\text{'})\; \backslash ,,\}$

по сути свертка,

$C\; (\Delta )\; =\; C\; (x\; -\; x\; ″)\; =\; \int \; x\; \prime \; A\; (x\; -\; x\; \prime )\; B\; (x\; \prime \; -\; x\; ″)\; =\; \int \; y\; A\; (\Delta \; -\; y)\; B\; (y).\; \{\backslash \; Displaystyle\; C\; (\backslash \; Delta)\; =\; C\; (x-x\; \text{'}\text{'})\; =\; \backslash \; int\; \_\; \{x\; \text{'}\}\; A\; (x-x\text{'})\; B\; (x\text{'}-x\; \text{'}\text{'})\; =\; \backslash \; int\; \_\; \{y\}\; A\; (\; \backslash \; Delta\; -y)\; B\; (y)\; \backslash ,.\}$

Экспонента может быть определена в диапазоне ts, который включает комплексные значения, пока интегралы по ядру распространения остаются сходящимися,

$K\; z\; (x)\; =\; е\; -\; z\; H.\; \{\backslash \; displaystyle\; K\_\; \{z\}\; (x)\; =\; e\; ^\; \{-\; zH\}\; \backslash ,.\}$

Пока действительная часть z положительна, при больших значениях x K экспоненциально убывает, а интегралы по K действительно абсолютно сходятся.

Предел этого выражения для z, приближающегося к чисто мнимой оси, - это встреченный выше пропагатор Шредингера,

$K\; t\; S\; chr\; =\; K\; it\; +\; ϵ\; =\; e\; -\; (it\; +\; ϵ)\; H,\; \{\backslash \; displaystyle\; K\_\; \{t\}\; ^\; \{\backslash \; rm\; \{Schr\}\}\; =\; K\_\; \{it\; +\; \backslash \; epsilon\}\; =\; e\; ^\; \{-\; (it\; +\; \backslash \; epsilon)\; H\}\; \backslash ,,\}$

, который иллюстрирует приведенную выше временную эволюцию гауссианов.

Исходя из основного тождества возведения в степень или интегрирования по путям,

$K\; z\; \ast \; K\; z\; \prime \; =\; K\; z\; +\; z\; \prime \; \{\backslash \; displaystyle\; K\_\; \{z\}\; *\; K\_\; \{z\; \text{'}\}\; =\; K\_\; \{z\; +\; z\; \text{'}\}\; \backslash ,\}$

выполняется для всех комплексных значений z, где интегралы абсолютно сходятся, так что операторы хорошо определены.

Таким образом, квантовая эволюция гауссиана, который является комплексным диффузионным ядром K,

$\psi \; 0\; (x)\; =\; K\; a\; (x)\; =\; K\; a\; \ast \; \delta \; (x)\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{0\}\; (x)\; =\; K\_\; \{a\}\; (x)\; =\; K\_\; \{a\}\; *\; \backslash \; delta\; (x)\; \backslash ,\}$

составляет состояние, эволюционирующее во времени,

$\psi \; t\; =\; K\; it\; \ast \; K\; a\; =\; K\; a\; +\; it.\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{t\}\; =\; K\_\; \{it\}\; *\; K\_\; \{a\}\; =\; K\_\; \{a\; +\; it\}\; \backslash ,.\}$

Это иллюстрирует приведенную выше диффузную форму сложных гауссовских решений,

$\psi \; t\; (x)\; знак\; равно\; 1\; 2\; \pi \; (a\; +\; it)\; e\; -\; x\; 2\; 2\; (a\; +\; it).\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{t\}\; (x)\; =\; \{1\; \backslash \; over\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; (a\; +\; it)\}\}\}\; e\; ^\; \{-\; \{x\; ^\; \{2\}\; \backslash \; over\; 2\; (a\; +\; it)\; \}\}\; \backslash ,.\}$

См. Также

Волна Распространение волны Анализ Фурье Групповая скорость Фазовая скорость Свободная частица

Когерентные состояния Форма волны Вейвлет Волна материи Уравнение Шредингера Введение в квантовую механику Солитон

Примечания

Примечания

Ссылки

• Эйнштейн, Альберт (1905), «Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (Об эвристической точке зрения на производство и преобразование света)» (PDF), Annalen der Physik, 17(6): 132–148, Bibcode : 1905AnP... 322..132E, doi : 10.1002 / andp.19053220607 Эта статья annus mirabilis о фотоэлектрическом эффекте была получена Annalen der Physik 18 марта 1905 г.
• Schiff, Leonard I. (1968), Quantum Mechanics (третье изд.), Лондон: МакГроу-Хилл
• Джой Маннерс (2000), Quantum Physics: An Introduction, CRC Press, pp. 53–56, ISBN 978-0-7503-0720-8
• Паули, Вольфганг (2000), Wave Механика: Том 5 лекций Паули по физике, Книги по физике, Dover Publications, ISBN 978-0486414621
• Abers, E.; Пирсон, Эд (2004), Quantum Mechanics, Addison Wesley, Prentice-Hall Inc., ISBN 978-0-13-146100-0
• Ричард Фицпатрик, Колебания и волны
• Берри, М.В. Balazs, NL (1979), "Нераспространяющиеся волновые пакеты", Am J Phys, 47 (47): 264–267, Bibcode : 1979AmJPh..47..264B, doi : 10.1119 / 1.11855
• Джексон, JD (1975), Classical Electrodynamics (2 ed.), New York: John Wiley Sons, Inc., ISBN 978-0-471-43132-9
• Фейнман, Р.П. ; Hibbs, AR (1965), Quantum Mechanics and Path Integrals, New York: McGraw-Hill, ISBN 978-0-07-020650- 2 (Довер, 2010, ISBN 0-486-47722-3.)
• Уилер, Николас (2004),

Внешние ссылки

• Обучение материалы, связанные с движением волнового пакета в Викиверситете
• Словарь определения волнового пакета в Викисловаре
• 1d график волнового пакета в Google
• 1d волновой цикл и график плотности вероятности в Google
• график пакета 2d волн в Google
• график последовательности 2d волн в Google
• график плотности вероятности 2d в Google
• Симуляция пакета волн в 2D (согласно FOURIER-Synthesis в 2D)
• Curtright, TL, Зависящие от времени функции Вигнера
• Web-Schödinger : интерактивное двумерное моделирование динамики волновых пакетов