| Часть серии о | ||||
| Физическая космология | ||||
|---|---|---|---|---|
 | ||||
Ранняя вселенная
| ||||
| Расширение Будущее | ||||
Компоненты Структура
| ||||
| Эксперименты | ||||
| Ученые | ||||
| История темы | ||||
| ||||
|
Закон Хаббла, также известный как закон Хаббла – Леметра, представляет собой наблюдение в физической космологии, согласно которому галактики удаляются от Земли со скоростью, пропорциональной их расстоянию. Другими словами, чем дальше они находятся, тем быстрее удаляются от Земли. Скорость галактик определяется их красным смещением, смещением света, который они излучают, в сторону красного конца видимого спектра.
Закон Хаббла считается первой наблюдательной базой для расширения Вселенной, и сегодня он служит одним из свидетельств, наиболее часто приводимых в поддержку модели Большого взрыва. Движение астрономических объектов, вызванное исключительно этим расширением, известно как поток Хаббла. Он описывается уравнением v = H 0 D, где H 0 - это константа пропорциональности - постоянная Хаббла - между «надлежащим расстоянием» D до галактики, которое может меняться со временем, в отличие от сопутствующего расстояния, и скоростью ее отделения. v, т.е. производная собственного расстояния по космологической координате времени. (См. « Использование правильного расстояния » для обсуждения тонкостей этого определения «скорости».)
Постоянная Хаббла чаще всего указывается в ( км / с ) / Мпк, что дает скорость в км / с галактики на расстоянии 1 мегапарсек (3,09 × 10 19 км), и ее значение составляет около 70 (км / с) / Мпк.. Однако единица СИ для H 0 - это просто с -1, а единица СИ для величины, обратной H 0, - это просто секунда. Величина, обратная H 0, известна как время Хаббла. Постоянную Хаббла также можно интерпретировать как относительную скорость расширения. В этой форме H 0 = 7% / млрд лет, что означает, что при нынешних темпах расширения несвязанная структура вырастет на 7% за миллиард лет.
Хотя идея расширения Вселенной с вычислимой скоростью широко приписывается Эдвину Хабблу, она была впервые выведена из уравнений общей теории относительности в 1922 году Александром Фридманом. Фридман опубликовал набор уравнений, теперь известных как уравнения Фридмана, показывающих, что Вселенная могла бы расширяться, и описывающих скорость расширения, если бы это было так. Затем Жорж Лемэтр в статье 1927 года независимо вывел, что Вселенная может расширяться, заметил пропорциональность между скоростью удаления и расстоянием до удаленных тел и предложил расчетное значение константы пропорциональности; Эта константа, когда Эдвин Хаббл подтвердил существование космического расширения и определил более точное значение для него два года спустя, стала известна под его именем как постоянная Хаббла. Хаббл сделал вывод о скорости разлета объектов по их красным смещениям, многие из которых были ранее измерены и связаны со скоростью Весто Слайфер в 1917 году. Хотя постоянная Хаббла H 0 примерно постоянна в пространстве скорость-расстояние в любой данный момент времени, параметр Хаббла H, которой постоянная Хаббла является текущее значение, изменяется со временем, так что термин константа иногда рассматривать как - то неправильным.
 Три шага к постоянной Хаббла
Три шага к постоянной Хаббла За десять лет до Хаббл сделал свои наблюдения, ряд физиков и математиков создал последовательную теорию расширяющейся Вселенной с помощью уравнений поля Эйнштейна по общей теории относительности. Применение самых общих принципов к природе вселенной привело к динамическому решению, которое противоречило преобладающему в то время представлению о статической вселенной.
В 1912 году Весто Слайфер измерил первое доплеровское смещение « спиральной туманности » (устаревший термин для спиральных галактик) и вскоре обнаружил, что почти все такие туманности удалялись от Земли. Он не понимал космологических последствий этого факта, и действительно, в то время было очень спорно, были ли эти туманности «островными вселенными» за пределами нашего Млечного Пути.
В 1922 году Александр Фридман вывел свои уравнения Фридмана из уравнений поля Эйнштейна, показав, что Вселенная может расширяться со скоростью, вычисляемой с помощью этих уравнений. Параметр, используемый Фридманом, известен сегодня как масштабный коэффициент и может рассматриваться как масштабно-инвариантная форма константы пропорциональности закона Хаббла. Жорж Лемэтр независимо нашел подобное решение в своей статье 1927 года, обсуждаемой в следующем разделе. Уравнения Фридмана выводятся путем вставки метрики для однородной и изотропной Вселенной в уравнения поля Эйнштейна для жидкости с заданной плотностью и давлением. Эта идея расширяющегося пространства-времени в конечном итоге приведет к космологии теории Большого взрыва и Устойчивого состояния.
В 1927 году, за два года до того, как Хаббл опубликовал свою статью, бельгийский священник и астроном Жорж Леметр первым опубликовал исследование, основанное на том, что сейчас известно как закон Хаббла. По словам канадского астронома Сиднея ван ден Берга, «открытие Леметром расширения Вселенной в 1927 году было опубликовано на французском языке в журнале, посвященном малым ударам. В переводе этой статьи на английский язык в 1931 году критическое уравнение было изменено. опуская ссылку на то, что сейчас известно как постоянная Хаббла ". Теперь известно, что изменения в переведенной статье были выполнены самим Лемэтром.
До появления современной космологии много говорилось о размере и форме Вселенной. В 1920 г. по этому поводу между Харлоу Шепли и Хибером Д. Кертисом состоялись дебаты Шепли-Кертиса. Шепли утверждал, что Вселенная размером с галактику Млечный Путь была маленькой, а Кертис утверждал, что Вселенная намного больше. Проблема была решена в ближайшее десятилетие с улучшенными наблюдениями Хаббла.
Эдвин Хаббл провел большую часть своих профессиональных астрономических наблюдений в обсерватории Маунт-Вильсон, где находился самый мощный телескоп в мире на то время. Его наблюдения переменных звезд- цефеид в «спиральных туманностях» позволили ему вычислить расстояния до этих объектов. Удивительно, но было обнаружено, что эти объекты находятся на таких расстояниях, которые помещают их далеко за пределы Млечного Пути. Их продолжали называть туманностями, и лишь постепенно термин « галактики» заменил его.
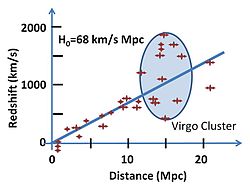 Подгонка скорости красного смещения закону Хаббла. Существуют различные оценки постоянной Хаббла. Группа HST Key H 0 подобрала сверхновые типа Ia для красных смещений от 0,01 до 0,1 и обнаружила, что H 0 = 71 ± 2 (статистический) ± 6 (систематический) км с −1 Мпк −1, в то время как Sandage et al. найти H 0 = 62,3 ± 1,3 (статистическое) ± 5 (систематическое) км с −1 Мпк −1.
Подгонка скорости красного смещения закону Хаббла. Существуют различные оценки постоянной Хаббла. Группа HST Key H 0 подобрала сверхновые типа Ia для красных смещений от 0,01 до 0,1 и обнаружила, что H 0 = 71 ± 2 (статистический) ± 6 (систематический) км с −1 Мпк −1, в то время как Sandage et al. найти H 0 = 62,3 ± 1,3 (статистическое) ± 5 (систематическое) км с −1 Мпк −1. Параметры, которые фигурируют в законе Хаббла, скорости и расстояния, напрямую не измеряются. В действительности мы определяем, скажем, яркость сверхновой, которая дает информацию о расстоянии до нее, и красное смещение z = ∆ λ / λ ее спектра излучения. Хаббл коррелировал яркость и параметр z.
Объединив свои измерения расстояний до галактик с измерениями красных смещений галактик Весто Слайфер и Милтона Хьюмасона, Хаббл обнаружил грубую пропорциональность между красным смещением объекта и его расстоянием. Хотя имел место значительный разброс (теперь известно, что он вызван пекулярными скоростями - «поток Хаббла» используется для обозначения области пространства, находящейся достаточно далеко, чтобы скорость удаления больше, чем местные пекулярные скорости), Хабблу удалось построить график. линия тренда от 46 галактик, которые он изучил, и получила значение постоянной Хаббла 500 км / с / Мпк (намного выше, чем принятое в настоящее время значение из-за ошибок в его калибровке расстояний; подробности см. в лестнице космических расстояний ).
Во время открытия и развития закона Хаббла было приемлемо объяснять феномен красного смещения как доплеровский сдвиг в контексте специальной теории относительности и использовать формулу Доплера, чтобы связать красное смещение z со скоростью. Сегодня, в контексте общей теории относительности, скорость между удаленными объектами зависит от выбора используемых координат, и поэтому красное смещение можно в равной степени описать как доплеровский сдвиг или космологический сдвиг (или гравитационный) из-за расширяющегося пространства, или как сочетание двух.
Закон Хаббла можно легко изобразить на «диаграмме Хаббла», на которой скорость (предполагаемая приблизительно пропорциональной красному смещению) объекта отложена в зависимости от его расстояния от наблюдателя. Прямая линия с положительным наклоном на этой диаграмме является визуальным изображением закона Хаббла.
После того, как открытие Хаббла было опубликовано, Альберт Эйнштейн отказался от своей работы по космологической постоянной, которую он разработал, чтобы модифицировать свои уравнения общей теории относительности, чтобы они могли дать статическое решение, которое, по его мнению, было правильным состоянием Вселенной. Уравнения Эйнштейна в их простейшей форме модели генерировали либо расширяющуюся, либо сжимающуюся Вселенную, поэтому космологическая постоянная Эйнштейна была искусственно создана, чтобы противодействовать расширению или сжатию, чтобы получить идеальную статическую и плоскую Вселенную. После открытия Хабблом того факта, что Вселенная расширяется, Эйнштейн назвал свое ошибочное предположение о том, что Вселенная статична, своей «самой большой ошибкой». Сама по себе общая теория относительности могла предсказать расширение Вселенной, которое (посредством наблюдений, таких как искривление света большими массами или прецессия орбиты Меркурия ) можно было экспериментально наблюдать и сравнивать с его теоретическими расчетами с использованием конкретных решений. уравнений, которые он изначально сформулировал.
В 1931 году Эйнштейн совершил поездку в обсерваторию Маунт-Вильсон, чтобы поблагодарить Хаббла за предоставление наблюдательной основы для современной космологии.
Космологическая постоянная вновь привлекла внимание в последние десятилетия как гипотеза темной энергии.
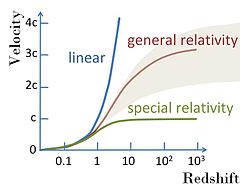 Множество возможных функций скорости рецессии в зависимости от красного смещения, включая простую линейную зависимость v = cz ; множество возможных форм из теорий, связанных с общей теорией относительности; и кривая, которая не допускает скорости выше скорости света в соответствии со специальной теорией относительности. Все кривые линейны при малых красных смещениях. См. Дэвиса и Лайнуивера.
Множество возможных функций скорости рецессии в зависимости от красного смещения, включая простую линейную зависимость v = cz ; множество возможных форм из теорий, связанных с общей теорией относительности; и кривая, которая не допускает скорости выше скорости света в соответствии со специальной теорией относительности. Все кривые линейны при малых красных смещениях. См. Дэвиса и Лайнуивера. Открытие линейной зависимости между красным смещением и расстоянием в сочетании с предполагаемой линейной зависимостью между скоростью рецессии и красным смещением дает прямое математическое выражение для закона Хаббла следующим образом:
куда
Закон Хаббла считается фундаментальным соотношением между скоростью разбегания и расстоянием. Однако связь между скоростью удаления и красным смещением зависит от принятой космологической модели и не устанавливается, за исключением небольших красных смещений.
Для расстояний D, превышающих радиус сферы Хаббла r HS , объекты удаляются со скоростью, превышающей скорость света ( см. Использование правильного расстояния для обсуждения значения этого):
Поскольку «постоянная» Хаббла является постоянной только в пространстве, а не во времени, радиус сферы Хаббла может увеличиваться или уменьшаться в различные промежутки времени. Нижний индекс «0» указывает значение постоянной Хаббла на сегодняшний день. Текущие данные свидетельствуют о том, что расширение Вселенной ускоряется ( см. Ускорение Вселенной ), а это означает, что для любой данной галактики скорость удаления dD / dt увеличивается со временем по мере того, как галактика перемещается на все большие и большие расстояния; однако на самом деле считается, что параметр Хаббла уменьшается со временем, а это означает, что если бы мы смотрели на некоторое фиксированное расстояние D и наблюдали, как несколько разных галактик проходят это расстояние, более поздние галактики пройдут это расстояние с меньшей скоростью, чем предыдущие..
Красное смещение можно измерить, определив длину волны известного перехода, например α-линии водорода для далеких квазаров, и найдя относительный сдвиг по сравнению со стационарным эталоном. Таким образом, красное смещение - величина, однозначная для экспериментального наблюдения. Другое дело - отношение красного смещения к скорости разбегания. Подробное обсуждение см. В Harrison.
Красное смещение z часто описывается как скорость красного смещения, которая представляет собой скорость рецессии, которая произвела бы такое же красное смещение, если бы оно было вызвано линейным эффектом Доплера (что, однако, не так, поскольку смещение частично вызвано космологическое расширение пространства и потому, что задействованные скорости слишком велики, чтобы использовать нерелятивистскую формулу для доплеровского сдвига). Эта скорость красного смещения может легко превысить скорость света. Другими словами, чтобы определить скорость красного смещения v rs, соотношение:
используется. То есть нет принципиальной разницы между скоростью красного смещения и красным смещением: они строго пропорциональны и не связаны никакими теоретическими рассуждениями. Мотивация за терминологией «скорость красного смещения» заключается в том, что скорость красного смещения согласуется со скоростью из низкоскоростного упрощения так называемой формулы Физо-Доплера.
Здесь λ o, λ e - наблюдаемая и излучаемая длины волн соответственно. Однако «скорость красного смещения» v rs не так просто связана с реальной скоростью при более высоких скоростях, и эта терминология приводит к путанице, если ее интерпретировать как реальную скорость. Далее обсуждается связь между скоростью красного или красного смещения и скоростью отступления. Это обсуждение основано на Сартори.
Предположим, что R (t) называется масштабным фактором Вселенной и увеличивается по мере расширения Вселенной в зависимости от выбранной космологической модели. Смысл ее в том, что все измеряется соответствующие расстояния D (т) между совместно движущихся точек возрастает пропорционально R. (Совместно движущиеся точки не перемещаются относительно друг друга, кроме как в результате расширения пространства.) Другими словами:
где t 0 - некоторое эталонное время. Если свет излучается галактикой в момент времени t e и принимается нами в момент t 0, он смещается в красную сторону из-за расширения пространства, и это красное смещение z будет просто:
Предположим, что галактика находится на расстоянии D, и это расстояние изменяется со временем со скоростью д т Д. Мы называем эту скорость спада "скоростью спада" v r:
Теперь определим постоянную Хаббла как
и откройте для себя закон Хаббла:
С этой точки зрения закон Хаббла представляет собой фундаментальное соотношение между (i) скоростью удаления, вносимой расширением пространства, и (ii) расстоянием до объекта; связь между красным смещением и расстоянием - это костыль, используемый для связи закона Хаббла с наблюдениями. Этот закон можно приблизительно связать с красным смещением z, сделав разложение в ряд Тейлора :
Если расстояние не слишком велико, все остальные усложнения модели превращаются в небольшие поправки, а временной интервал - это просто расстояние, деленное на скорость света:
или
Согласно этому подходу, отношение cz = v r является приближением, допустимым для малых красных смещений, которое должно быть заменено отношением для больших красных смещений, которое зависит от модели. См. Рисунок "скорость-красное смещение".
Строго говоря, ни v, ни D в формуле не наблюдаются напрямую, потому что сейчас они являются свойствами галактики, тогда как наши наблюдения относятся к галактике в прошлом, в то время, когда свет, который мы сейчас видим, покинул ее.
Для относительно близких галактик (красное смещение z намного меньше единицы) v и D не сильно изменится, и v можно оценить по формуле, где c - скорость света. Это дает эмпирическую зависимость, найденную Хабблом.
Для далеких галактик v (или D) нельзя вычислить по z без определения подробной модели того, как H изменяется со временем. Красное смещение даже не связано напрямую со скоростью удаления в момент выхода света, но у него есть простая интерпретация: (1 + z) - это коэффициент, с которым Вселенная расширилась, пока фотон двигался к наблюдателю.
При использовании закона Хаббла для определения расстояний можно использовать только скорость, обусловленную расширением Вселенной. Поскольку гравитационно взаимодействующие галактики движутся относительно друг друга независимо от расширения Вселенной, эти относительные скорости, называемые пекулярными скоростями, необходимо учитывать при применении закона Хаббла.
Эффект « Палец Бога» - один из результатов этого явления. В системах, связанных гравитацией, таких как галактики или наша планетная система, расширение пространства является гораздо более слабым эффектом, чем сила притяжения гравитации.
Этот параметр обычно называют « постоянной Хаббла », но это неправильное название, поскольку он постоянен в пространстве только в фиксированное время; она меняется со временем почти во всех космологических моделях, и все наблюдения далеких объектов также являются наблюдениями в далеком прошлом, когда «константа» имела другое значение. « Параметр Хаббла » - более правильный термин, обозначающий современное значение.
Другой распространенный источник путаницы состоит в том, что ускорение Вселенной не означает, что параметр Хаббла действительно увеличивается со временем; так как в большинстве ускоряющих моделей увеличивается относительно быстрее, чем, поэтому H уменьшается со временем. (Скорость удаления одной выбранной галактики действительно увеличивается, но разные галактики, проходящие через сферу фиксированного радиуса, в более поздние времена пересекают сферу медленнее.)
Об определении безразмерного параметра замедления
Из этого видно, что параметр Хаббла уменьшается со временем, если только ; последнее может произойти только в том случае, если Вселенная содержит фантомную энергию, которая теоретически считается маловероятной.
Тем не менее, в стандартной модели ΛCDM, будет иметь тенденцию к -1 сверху в отдаленном будущем как космологические становится все более доминирующей над материей; это означает, что сверху будет приближаться к постоянному значению км / с / Мпк, и тогда масштабный фактор Вселенной будет экспоненциально расти во времени.
Математический вывод идеализированного закона Хаббла для равномерно расширяющейся Вселенной представляет собой довольно элементарную теорему геометрии в трехмерном декартовом / ньютоновском координатном пространстве, которое, рассматриваемое как метрическое пространство, является полностью однородным и изотропным (свойства не меняются в зависимости от местоположения). или направление). Проще говоря, теорема такова:
Любые две точки, которые удаляются от начала координат, каждая по прямым линиям и со скоростью, пропорциональной расстоянию от начала координат, будут удаляться друг от друга со скоростью, пропорциональной их расстоянию друг от друга.
Фактически это применимо к недекартовским пространствам, если они локально однородны и изотропны, особенно к отрицательно и положительно искривленным пространствам, часто рассматриваемым как космологические модели (см. Форму Вселенной ).
Наблюдение, вытекающее из этой теоремы, состоит в том, что наблюдение за удаляющимися от нас объектами на Земле не является признаком того, что Земля находится близко к центру, от которого происходит расширение, а скорее то, что каждый наблюдатель в расширяющейся Вселенной будет видеть объекты, удаляющиеся от них.
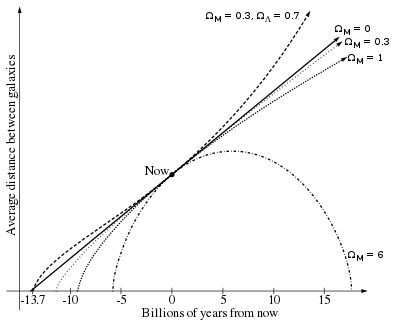 Возраст и конечная судьба Вселенной может быть определена путем измерения постоянной Хаббла сегодня и экстраполяцию с наблюдаемым значением параметра замедления, однозначно характеризуется значениями параметров плотности (Q M для материи и Ом Л для темной энергии). «Замкнутая вселенная» с Ω M gt; 1 и Ω Λ = 0 заканчивается Большим сжатием и значительно моложе своего хаббловского возраста. «Открытая вселенная» с Ω M ≤ 1 и Ω Λ = 0 постоянно расширяется и имеет возраст, который ближе к ее хаббловскому возрасту. Для ускоряющейся Вселенной с ненулевым Ω Λ, в которой мы живем, возраст Вселенной по совпадению очень близок к возрасту Хаббла.
Возраст и конечная судьба Вселенной может быть определена путем измерения постоянной Хаббла сегодня и экстраполяцию с наблюдаемым значением параметра замедления, однозначно характеризуется значениями параметров плотности (Q M для материи и Ом Л для темной энергии). «Замкнутая вселенная» с Ω M gt; 1 и Ω Λ = 0 заканчивается Большим сжатием и значительно моложе своего хаббловского возраста. «Открытая вселенная» с Ω M ≤ 1 и Ω Λ = 0 постоянно расширяется и имеет возраст, который ближе к ее хаббловскому возрасту. Для ускоряющейся Вселенной с ненулевым Ω Λ, в которой мы живем, возраст Вселенной по совпадению очень близок к возрасту Хаббла. Значение параметра Хаббла изменяется со временем, увеличиваясь или уменьшаясь в зависимости от значения так называемого параметра замедления, который определяется
Во Вселенной с параметром замедления, равным нулю, следует, что H = 1 / t, где t - время с момента Большого взрыва. Ненулевое, зависящее от времени значение просто требует интегрирования уравнений Фридмана в обратном направлении от настоящего времени до времени, когда размер сопутствующего горизонта был равен нулю.
Долгое время считалось, что q было положительным, что указывало на то, что расширение замедляется из-за гравитационного притяжения. Это означало бы возраст Вселенной менее 1 / H (что составляет около 14 миллиардов лет). Например, значение q, равное 1/2 (когда-то одобренное большинством теоретиков), даст возраст Вселенной как 2 / (3 H). Открытие в 1998 году, что д - видимому, отрицательные означает, что Вселенная может быть на самом деле старше, чем 1 / H. Тем не менее, оценки возраста Вселенной очень близко к 1 / H.
Расширение пространства, резюмируемое интерпретацией закона Хаббла в рамках теории Большого взрыва, имеет отношение к старой загадке, известной как парадокс Ольберса : если бы Вселенная была бесконечной по размеру, статичной и заполнена равномерным распределением звезд, тогда все лучи зрения в небо заканчивалось бы звездой, и небо было бы ярким, как поверхность звезды. Однако ночное небо в основном темное.
С XVII века астрономы и другие мыслители предложили множество возможных способов разрешения этого парадокса, но принятое в настоящее время решение частично зависит от теории Большого взрыва, а частично от расширения Хаббла: во Вселенной, существующей в ограниченном количестве Со временем только свет конечного числа звезд успел достичь нас, и парадокс разрешен. Кроме того, в расширяющейся Вселенной далекие объекты удаляются от нас, из-за чего исходящий от них свет смещается в красную сторону и становится менее ярким к тому времени, когда мы его видим.
Вместо работы с постоянной Хаббла обычно вводят безразмерную постоянную Хаббла, обычно обозначаемую h, и записывают постоянную Хаббла H 0 как h × 100 км с −1 Мпк −1, всю относительную неопределенность истинного значения из H 0 переводится в h. Безразмерная постоянная Хаббла часто используется для определения расстояний, которые рассчитываются по красному смещению z по формуле d ≈ c /H 0× z. Поскольку H 0 точно неизвестно, расстояние выражается как:
Другими словами, вычисляется 2998 × z и единицы задаются как или
Иногда может быть выбрано справочное значение, отличное от 100, и в этом случае после h ставится нижний индекс, чтобы избежать путаницы; например, h 70 означает, что подразумевает.
Это не следует путать с безразмерным значением постоянной Хаббла, обычно выражаемой в единицах Планка, полученным путем умножения H 0 на 1,75 × 10 -63 (из определений парсек и t P ), например, для H 0 = 70, получается вариант единицы Планка 1.2 × 10 −61.
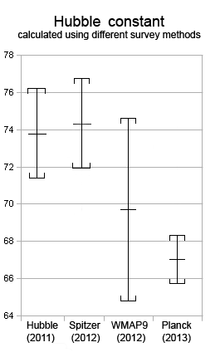 Значение постоянной Хаббла, включая неопределенность измерений для недавних съемок
Значение постоянной Хаббла, включая неопределенность измерений для недавних съемок Значение постоянной Хаббла оценивается путем измерения красного смещения далеких галактик и последующего определения расстояний до них каким-либо другим методом, кроме закона Хаббла. Этот подход является частью лестницы космических расстояний для измерения расстояний до внегалактических объектов. Неопределенности в физических допущениях, используемых для определения этих расстояний, привели к различным оценкам постоянной Хаббла.
Наблюдения астронома Вальтера Бааде привели его к определению различных « популяций » звезд (Население I и Население II). Те же наблюдения привели его к открытию, что существует два типа переменных звезд цефеид. Используя это открытие, он пересчитал размер известной Вселенной, удвоив предыдущий расчет, сделанный Хабблом в 1929 году. Он объявил об этом открытии, к значительному изумлению, на встрече Международного астрономического союза в 1952 году в Риме.
В октябре 2018 года ученые представили новый третий способ (два более ранних метода, один из которых основан на красных смещениях, а другой - на лестнице космических расстояний, дали результаты, которые не совпадают), с использованием информации о гравитационно-волновых событиях (особенно тех, которые связаны с слиянием нейтронных звезд)., как GW170817 ), определения постоянной Хаббла.
В июле 2019 года астрономы сообщили, что после обнаружения слияния нейтронных звезд GW170817 был предложен новый метод определения постоянной Хаббла и устранения расхождений с более ранними методами, основанный на слиянии пар нейтронных звезд. известная как темная сирена. Их измерение постоянной Хаббла73,3+5,3 −5,0 (км / с) / Мпк.
Также в июле 2019 года астрономы сообщили о другом новом методе, использующем данные космического телескопа Хаббла и основанном на расстояниях до звезд красных гигантов, рассчитанных с использованием индикатора расстояния ветви красных гигантов (TRGB). Их измерение постоянной Хаббла69,8+1,9 -1,9 (км / с) / Мпк.
На протяжении большей части второй половины 20-го века значение составляло от 50 до 90 (км / с) / Мпк.
Значение постоянной Хаббла было темой долгого и довольно ожесточенного спора между Жераром де Вокулёром, который утверждал, что значение составляет около 100, и Алланом Сэндиджем, который утверждал, что значение было около 50. В 1996 году дебаты модерировал Джон Бахколл. между Сиднеем ван ден Бергом и Густавом Тамманном проходил аналогично более ранним дебатам Шепли-Кертиса по поводу этих двух конкурирующих ценностей.
Эта ранее значительная разница в оценках была частично устранена с введением в конце 1990-х годов модели Вселенной ΛCDM. С помощью модели ΛCDM наблюдения скоплений с большим красным смещением в рентгеновском и микроволновом диапазонах волн с использованием эффекта Сюняева – Зельдовича, измерения анизотропии космического микроволнового фонового излучения и оптические обзоры дали значение константы около 70.
Более поздние измерения миссии Planck, опубликованные в 2018 году, указывают на более низкое значение67,66 ± 0,42, хотя даже совсем недавно, в марте 2019 г., более высокое значение74,03 ± 1,42 было определено с использованием усовершенствованной процедуры с использованием космического телескопа Хаббл. Эти два измерения расходятся на уровне 4,4 σ, за пределами вероятного уровня случайности. Разрешение этого разногласия - постоянная область исследований.
См. Таблицу измерений ниже для многих недавних и более старых измерений.
Значение, полученное при стандартных наблюдениях за сверхновыми типа Ia со свечой, которое в 1998 году было определено как отрицательное, удивило многих астрономов, сделав вывод о том, что расширение Вселенной в настоящее время "ускоряется" (хотя фактор Хаббла все еще уменьшается со временем, как упоминалось выше в разделе « Интерпретация »; см. статьи о темной энергии и модели ΛCDM ).
Начнем с уравнения Фридмана :
где - параметр Хаббла, - масштабный коэффициент, G - гравитационная постоянная, - нормализованная пространственная кривизна Вселенной, равная -1, 0 или 1, и - космологическая постоянная.
Если во Вселенной преобладает материя, то массовая плотность Вселенной может просто включать материю, так что
где плотность материи сегодня. Из уравнения Фридмана и принципов термодинамики мы знаем, что для нерелятивистских частиц их массовая плотность уменьшается пропорционально обратному объему Вселенной, поэтому приведенное выше уравнение должно быть верным. Мы также можем определить (см. Параметр плотности для)
следовательно:
Также по определению
где нижний индекс ноль относится к сегодняшним значениям, а. Подставляя все это в уравнение Фридмана в начале этого раздела и заменяя его на, дает
Если во Вселенной преобладает как материя, так и темная энергия, то приведенное выше уравнение для параметра Хаббла также будет функцией уравнения состояния темной энергии. А сейчас:
где - массовая плотность темной энергии. По определению, уравнение состояния в космологии есть, и если его подставить в уравнение жидкости, которое описывает, как массовая плотность Вселенной изменяется со временем, тогда
Если w постоянно, то
подразумевая:
Таким образом, для темной энергии с постоянным уравнением состояния ш,. Если это подставить в уравнение Фридмана таким же образом, как и раньше, но на этот раз, который предполагает пространственно плоскую Вселенную, тогда (см. Форму Вселенной )
Если темная энергия происходит от космологической постоянной, такой как введенная Эйнштейном, это можно показать. Затем уравнение сводится к последнему уравнению в разделе вселенной, где преобладает материя, с установленным на ноль. В этом случае начальная плотность темной энергии определяется выражением
Если темная энергия не имеет постоянного уравнения состояния w, то
и чтобы решить эту проблему, он должен быть параметризован, например, если, давая
Другие ингредиенты были разработаны недавно.
Постоянная Хаббла имеет обратное время; время Хаббла t H просто определяется как величина, обратная постоянной Хаббла, т. е.
Это немного отличается от возраста Вселенной, который составляет примерно 13,8 миллиарда лет. Время Хаббла - это возраст, который у него был бы, если бы расширение было линейным, и оно отличается от реального возраста Вселенной, потому что расширение не линейное; они связаны безразмерным фактором, который зависит от массово-энергетического содержания Вселенной, которое составляет около 0,96 в стандартной модели ΛCDM.
В настоящее время мы, кажется, приближаемся к периоду, когда расширение Вселенной будет экспоненциальным из-за возрастающего преобладания энергии вакуума. В этом режиме параметр Хаббла постоянен, и Вселенная увеличивается в е раз каждый хаббловский раз:
Точно так же общепринятое значение 2,27 Es −1 означает, что (при нынешней скорости) Вселенная будет расти с коэффициентом в одну экзасекунду.
Как объяснялось выше, в течение длительных периодов времени динамика осложняется общей теорией относительности, темной энергией, инфляцией и т. Д.
Длина Хаббла или расстояние Хаббла - это единица расстояния в космологии, определяемая как - скорость света, умноженная на время Хаббла. Это эквивалентно 4550 миллионам парсеков или 14,4 миллиардам световых лет. (Числовое значение длины Хаббла в световых годах по определению равно значению времени Хаббла в годах.) Хаббловское расстояние - это расстояние между Землей и галактиками, которые в настоящее время удаляются от нас со скоростью свет, как можно видеть путем подстановки в уравнение для закона Хаббла, V = H 0 D.
Объем Хаббла иногда определяют как объем Вселенной с сопутствующим размером, равным 1. Точное определение варьируется: иногда его определяют как объем сферы с радиусом или, альтернативно, как боковой куб. Некоторые космологи даже используют термин объем Хаббла для обозначения относятся к объему наблюдаемой Вселенной, хотя его радиус примерно в три раза больше.
Для определения постоянной Хаббла использовалось несколько методов. Измерения "поздней вселенной" с использованием методов калиброванной лестницы расстояний сошлись на значении приблизительно73 км / с / Мпк. С 2000 года стали доступны методы "ранней вселенной", основанные на измерениях космического микроволнового фона, и они согласуются со значением, близким к 67,7 км / с / Мпк. (Это объясняет изменение скорости расширения со времен ранней Вселенной, поэтому сравнимо с первым числом.) По мере совершенствования методов оценочные погрешности измерений уменьшились, но диапазон измеренных значений не уменьшился до такой степени, что разногласия теперь статистически значимы. Это несоответствие называется напряжением Хаббла.
По состоянию на 2020 год причина несоответствия не выяснена. В апреле 2019 года астрономы сообщили о дальнейших существенных расхождениях между различными методами измерения в значениях постоянной Хаббла, что, возможно, свидетельствует о существовании новой области физики, которая в настоящее время недостаточно изучена. К ноябрю 2019 года это напряжение настолько выросло, что некоторые физики, такие как Джозеф Силк, стали называть его «возможным кризисом космологии», поскольку наблюдаемые свойства Вселенной кажутся несовместимыми. В феврале 2020 года проект Megamaser Cosmology Project опубликовал независимые результаты, которые подтвердили результаты дистанционной лестницы и отличались от результатов ранней вселенной на уровне статистической значимости 95%. В июле 2020 года измерения космического фонового излучения Космологическим телескопом Атакама предсказывают, что Вселенная должна расширяться медленнее, чем наблюдается в настоящее время.
 Оценочные значения постоянной Хаббла, 2001–2020 гг. Оценки, выделенные черным цветом, представляют собой калиброванные лестничные измерения расстояний, которые имеют тенденцию группироваться вокруг73 км / с / Мпк ; красный представляет измерения CMB / BAO ранней Вселенной с параметрами ΛCDM, которые показывают хорошее согласие с цифрой около67 км / с / Мпк, в то время как синий - это другие методы, неопределенности которых еще не достаточно малы, чтобы сделать выбор между ними.
Оценочные значения постоянной Хаббла, 2001–2020 гг. Оценки, выделенные черным цветом, представляют собой калиброванные лестничные измерения расстояний, которые имеют тенденцию группироваться вокруг73 км / с / Мпк ; красный представляет измерения CMB / BAO ранней Вселенной с параметрами ΛCDM, которые показывают хорошее согласие с цифрой около67 км / с / Мпк, в то время как синий - это другие методы, неопределенности которых еще не достаточно малы, чтобы сделать выбор между ними. | Дата публикации | Постоянная Хаббла (км / с) / Мпк | Наблюдатель | Цитата | Замечания / методология |
|---|---|---|---|---|
| 2020-12-16 | 72,1 ± 2,0 | Космический телескоп Хаббла и Gaia EDR3 | Объединение более ранних работ по звездам красных гигантов с использованием индикатора расстояния ветви красных гигантов (TRGB) с измерениями параллакса Омеги Центавра из Gaia EDR3. | |
| 2020-12-15 | 73,2 ± 1,3 | Космический телескоп Хаббла и Gaia EDR3 | Комбинация фотометрии HST и параллаксов Gaia EDR3 для цефеид Млечного Пути, снижающая неопределенность калибровки светимости цефеид до 1,0%. Общая неопределенность в значении составляет 1,8%, и ожидается, что она будет уменьшена до 1,3% с большей выборкой сверхновых типа Ia в галактиках, которые являются известными хозяевами цефеид. Продолжение сотрудничества, известного как Supernovae, по уравнению состояния темной энергии (SHoES). | |
| 2020-12-04 | 73,5 ± 5,3 | Э. Дж. Бакстер, Б. Д. Шервин | Гравитационное линзирование в CMB используется для оценки без привязки к шкале звукового горизонта, обеспечивая альтернативный метод анализа данных Planck. | |
| 2020-11-25 | 71,8+3,9 −3,3 | P. Denzel et al. | Восемь систем галактик с четырьмя линзами используются для определения с точностью до 5%, что согласуется как с «ранними», так и «поздними» оценками Вселенной. Независимо от дальних лестниц и космического микроволнового фона. | |
| 2020-11-07 | 67,4 ± 1,0 | T. Sedgwick et al. | Получено из 88 0,02 lt;lt; 0,05 сверхновых типа Ia, используемых в качестве стандартных индикаторов расстояния до свечей. Оценка корректируется с учетом эффектов, свойственных скоростей в средах сверхновых, по оценкам из поля плотности галактик. В результате предполагается, что Ω m = 0,3, Ω Λ = 0,7 и звуковой горизонт 149,3 Мпк, значение, взятое из Anderson et al. (2014). | |
| 2020-09-29 | 67,6+4,3 −4,2 | S. Mukherjee et al. | Гравитационные волны, если предположить, что переходный ZTF19abanrh, обнаруженный Zwicky Transient Facility, является оптическим аналогом GW190521. Независимо от дальних лестниц и космического микроволнового фона. | |
| 2020-06-18 | 75,8+5,2 -4,9 | T. de Jaeger et al. | Используйте сверхновые типа II в качестве стандартизируемых свечей, чтобы получить независимое измерение постоянной Хаббла - 7 SNe II с расстояниями между родительскими галактиками, измеренными по переменным цефеид или вершине ветви красных гигантов. | |
| 2020-02-26 | 73,9 ± 3,0 | Космологический проект Megamaser | Измерения геометрических расстояний до галактик, вмещающих мегамазеры. Независимо от дальних лестниц и космического микроволнового фона. | |
| 2019-10-14 | 74,2+2,7 −3,0 | ШАРИКИ | Моделирование распределения массы и временной задержки линзированного квазара DES J0408-5354. | |
| 2019-09-12 | 76,8 ± 2,6 | SHARP / H0LiCOW | Моделирование трех галактических линзированных объектов и их линз с использованием наземной адаптивной оптики и космического телескопа Хаббла. | |
| 2019-08-20 | 73,3+1,36 -1,35 | K. Dutta et al. | Это получено при анализе космологических данных с малым красным смещением в рамках модели ΛCDM. Используемые наборы данных - это сверхновые типа Ia, барионные акустические колебания, измерения временной задержки с использованием сильного линзирования, измерения с использованием космических хронометров и измерения роста на основе крупномасштабных наблюдений за структурой. | |
| 2019-08-15 | 73,5 ± 1,4 | MJ Reid, DW Pesce, AG Riess | Измерение расстояния до Мессье 106 с помощью его сверхмассивной черной дыры в сочетании с измерениями затменных двойных звезд в Большом Магеллановом Облаке. | |
| 2019-07-16 | 69,8 ± 1,9 | Космический телескоп Хаббла | Расстояния до звезд красных гигантов рассчитываются с помощью индикатора расстояния ветви красных гигантов (TRGB). | |
| 2019-07-10 | 73,3+1,7 -1,8 | H0LiCOW сотрудничество | Обновленные наблюдения многократно отображаемых квазаров, теперь с использованием шести квазаров, независимо от лестницы космических расстояний и независимых от измерений космического микроволнового фона. | |
| 2019-07-08 | 70,3+5,3 −5,0 | Детекторы LIGO и Virgo | Использует радиоволну GW170817 в сочетании с более ранними данными о гравитационных волнах (GW) и электромагнитных (EM) данных. | |
| 2019-03-28 | 68,0+4,2 −4,1 | Ферми-ЛАТ | Затухание гамма-излучения из-за внегалактического света. Независимо от космической дистанционной лестницы и космического микроволнового фона. | |
| 2019-03-18 | 74,03 ± 1,42 | Космический телескоп Хаббла | Прецизионная HST-фотометрия цефеид в Большом Магеллановом Облаке (БМО) снижает неопределенность расстояния до БМО с 2,5% до 1,3%. Пересмотр увеличивает напряжение с измерениями реликтового излучения до уровня 4,4 σ (P = 99,999% для гауссовых ошибок), увеличивая расхождение выше вероятного уровня случайности. Продолжение сотрудничества, известного как Supernovae, по уравнению состояния темной энергии (SHoES). | |
| 2019-02-08 | 67,780,91 -0,87 | Джозеф Райан и др. | Угловой размер квазара и барионные акустические колебания в предположении плоской модели LambdaCDM. Альтернативные модели приводят к другим (обычно более низким) значениям постоянной Хаббла. | |
| 2018-11-06 | 67,77 ± 1,30 | Обзор темной энергии | Измерения сверхновых с использованием метода обратной лестницы на основе барионных акустических колебаний. | |
| 2018-09-05 | 72,5+2,1 -2,3 | H0LiCOW сотрудничество | Наблюдения многократно отображаемых квазаров, не зависящие от лестницы космических расстояний и измерений космического микроволнового фона. | |
| 2018-07-18 | 67,66 ± 0,42 | Планка Миссия | Окончательные результаты Planck 2018. | |
| 2018-04-27 | 73,52 ± 1,62 | Космический телескоп Хаббла и Гайя | Дополнительная HST- фотометрия галактических цефеид с ранними измерениями параллакса Gaia. Пересмотренное значение увеличивает напряжение с измерениями реликтового излучения на уровне 3,8 σ. Продолжение сотрудничества SHoES. | |
| 2018-02-22 | 73,45 ± 1,66 | Космический телескоп Хаббла | Измерения параллакса галактических цефеид для улучшенной калибровки дистанционной лестницы ; значение указывает на расхождение с измерениями реликтового излучения на уровне 3.7 σ. Ожидается, что неопределенность снизится до менее 1% с окончательным выпуском каталога Gaia. ОБУВЬ сотрудничество. | |
| 2017-10-16 | 70,0+12,0 −8,0 | LIGO Scientific Collaboration и Дева Сотрудничество | Стандартное измерение сирены, не зависящее от обычных методов "стандартной свечи"; Гравитационно-волновой анализ слияния двойной нейтронной звезды (BNS) GW170817 непосредственно оценил расстояние светимости в космологических масштабах. Оценка пятидесяти подобных обнаружений в следующем десятилетии может разрешить противоречия с другими методологиями. Обнаружение и анализ слияния нейтронной звезды и черной дыры (NSBH) может обеспечить большую точность, чем может позволить BNS. | |
| 2016-11-22 | 71,9+2,4 −3,0 | Космический телескоп Хаббла | Использует временные задержки между несколькими изображениями удаленных переменных источников, созданными с помощью сильного гравитационного линзирования. Сотрудничество, известное как линзы в источнике COSMOGRAIL (H0LiCOW). | |
| 2016-08-04 | 76,2+3,4 -2,7 | Космические потоки-3 | Сравнение красного смещения с другими методами определения расстояний, включая методы Талли – Фишера, переменную цефеид и сверхновые типа Ia. Ограничительная оценка на основе данных предполагает более точное значение75 ± 2. | |
| 2016-07-13 | 67,6+0,7 −0,6 | SDSS-III Спектроскопическое исследование барионных колебаний (BOSS) | Барионные акустические колебания. Расширенное исследование (eBOSS) началось в 2014 году и, как ожидается, продлится до 2020 года. Расширенное исследование предназначено для изучения того времени, когда Вселенная уходила от эффектов замедления силы тяжести от 3 до 8 миллиардов лет после Большого взрыва. | |
| 2016-05-17 | 73,24 ± 1,74 | Космический телескоп Хаббла | Сверхновая типа Ia, ожидается, что неопределенность уменьшится более чем в два раза с предстоящими измерениями Gaia и другими улучшениями. ОБУВЬ сотрудничество. | |
| 2015-02 | 67,74 ± 0,46 | Планка Миссия | Результаты анализа Планка «s полной миссии были обнародованы на 1 декабря 2014 года на конференции в Ферраре, Италия. Полный комплект документов с подробным описанием результатов миссии был выпущен в феврале 2015 года. | |
| 2013-10-01 | 74,4 ± 3,0 | Космические потоки-2 | Сравнение красного смещения с другими методами определения расстояний, включая методы Талли – Фишера, переменную цефеид и сверхновые типа Ia. | |
| 2013-03-21 | 67,80 ± 0,77 | Планка Миссия | ESA Planck Surveyor был запущен в мае 2009 года в течение четырех лет, он выполнил значительно более детальное исследование космического микроволнового излучения, чем более ранние исследования с использованием НЕМТА радиометров и болометром технологии для измерения реликтового излучения в меньшем масштабе, чем WMAP. 21 марта 2013 года группа европейских исследователей космологического зонда Planck опубликовала данные миссии, включая новую карту CMB всего неба и их определение постоянной Хаббла. | |
| 2012-12-20 | 69,32 ± 0,80 | WMAP (9 лет) в сочетании с другими измерениями. | ||
| 2010 г. | 70,4+1,3 -1,4 | WMAP (7 лет) в сочетании с другими измерениями. | Эти значения возникают в результате подгонки комбинации WMAP и других космологических данных к простейшей версии модели ΛCDM. Если данные соответствуют более общим версиям, H 0 имеет тенденцию быть меньше и более неопределенным: обычно около67 ± 4 (км / с) / Мпк, хотя некоторые модели допускают значения около63 (км / с) / Мпк. | |
| 2010 г. | 71,0 ± 2,5 | Только WMAP (7 лет). | ||
| 2009-02 | 70,5 ± 1,3 | WMAP (5 лет) в сочетании с другими измерениями. | ||
| 2009-02 | 71,9+2,6 -2,7 | Только WMAP (5 лет) | ||
| 2007 г. | 70,4+1,5 -1,6 | WMAP (3 года) в сочетании с другими измерениями. | ||
| 2006-08 | 76,9+10,7 -8,7 | Рентгеновская обсерватория Чандра | Комбинированный эффект Сюняева – Зельдовича и рентгеновские наблюдения скоплений галактик Chandra. Скорректированная неопределенность в таблице из Planck Collaboration 2013. | |
| 2001-05 | 72 ± 8 | Ключевой проект космического телескопа Хаббл | Этот проект установил наиболее точное оптическое определение, совместимое с измерением H 0, основанным на наблюдениях эффекта Сюняева-Зельдовича многих скоплений галактик, имеющих аналогичную точность. | |
| до 1996 года | 50–90 (оценка) | |||
| начало 1970-х | ≈ 55 (оценка) | Аллан Сэндидж и Густав Тамманн | ||
| 1958 г. | 75 (оценка) | Аллан Сэндидж | Это первая хорошая оценка H 0, но консенсус будет достигнут через десятилетия. | |
| 1956 г. | 180 | Хьюмасон, Мэйолл и Сэндидж | ||
| 1929 г. | 500 | Эдвин Хаббл, телескоп Хукера | ||
| 1927 г. | 625 | Жорж Лемэтр | Первое измерение и интерпретация как признак расширения Вселенной |