В математике, фундаментальный многоугольник может быть определен для каждой компактной римановой поверхности рода больше 0. кодирует не только топологию поверхности через ее фундаментальную группу, но и определяет риманову поверхность до конформной эквивалентности. По теореме униформизации каждая компактная риманова поверхность имеет односвязную универсальную накрывающую поверхность, заданную ровно одним из следующих утверждений:
В первом случае нулевого рода поверхность конформно эквивалентна сфере Римана.
Во втором случае рода один, поверхность конформно эквивалентна тор С / Л для некоторой решетки Л в С. Фундаментальный многоугольник Λ, если считать его выпуклым, может быть взят либо за параллелограмм периодов, либо за центрально-симметричный шестиугольник - результат, впервые доказанный Федоровым в 1891 году.
В последнем случае род г gt; 1, риманова поверхность конформно эквивалентна Н / Г, где Γ является фуксова группа из преобразований Мёбиуса. Фундаментальная область для Г задаются выпуклым многоугольником для гиперболической метрики на Н. Они могут быть определены многоугольниками Дирихле и иметь четное число сторон. Строение фундаментальной группы Γ можно прочитать с такого многоугольника. Используя теорию квазиконформных отображений и уравнение Бельтрами, можно показать, что существует канонический выпуклый многоугольник Дирихле со сторонами 4 g, впервые определенный Фрике, который соответствует стандартному представлению Γ как группы с 2 g образующими a 1, b 1, a 2, b 2,..., a g, b g и единственное соотношение [ a 1, b 1 ] [ a 2, b 2 ] ⋅⋅⋅ [ a g, b g ] = 1, где [ a, b ] = a b a -1b -1.
Любая риманова метрика на ориентированном замкнутом двумерном многообразии M определяет комплексную структуру на M, что делает M компактной римановой поверхностью. Из использования фундаментальных многоугольников следует, что два ориентированных замкнутых 2-многообразия классифицируются по их роду, который составляет половину ранга абелевой группы Γ / [Γ, Γ], где Γ = π 1 ( M). Более того, из теории квазиконформных отображений также следует, что две компактные римановы поверхности диффеоморфны тогда и только тогда, когда они гомеоморфны. Следовательно, два замкнутых ориентированных 2-многообразия гомеоморфны тогда и только тогда, когда они диффеоморфны. Такой результат можно доказать также методами дифференциальной топологии.


В случае рода один, фундаментальный выпуклый многоугольник ищется для действия по переводу Λ = Z ⊕ Z б на R 2 = C, где и Ь линейно независимы над R. (После выполнения вещественного линейного преобразования на R 2, можно предположить, если это необходимо, что Λ = Z 2 = Z + Z я ; для рода одной римановой поверхности оно может быть принято, чтобы иметь вид Λ = Z 2 = Z + Z ω, где Im ωgt; 0.) Фундаментальная область задается параллелограммом s x + t y для 0 lt; s, t lt;1, где x и y образующие Λ.
Если С есть внутренность фундаментального выпуклого многоугольника, то переводит C + х крышки R 2, как х пробегает Л. Отсюда следует, что граничные точки C образуются из пересечений C ∩ ( C + x). Эти компактные множества выпуклых в ∂ C и, таким образом, либо вершины C или стороны C. Отсюда следует, что так можно записать любую замкнутую сторону C. Перевод с - х следует, что C ∩ ( C - х) также является стороной C. Таким образом, стороны C образуют параллельные пары одинаковой длины. Конечные точки двух таких параллельных сегментов равной длины могут быть соединены таким образом, чтобы они пересекались, и пересечение происходило в средних точках отрезков прямой, соединяющих конечные точки. Отсюда следует, что пересечение всех таких отрезков происходит в одной точке. Если перевести эту точку в начало координат, то получится, что многоугольник центрально симметричен; то есть, если точка z находится в многоугольнике, то же самое - z.
Легко увидеть переводы центрально-симметричного выпуклого шестиугольника на мозаику плоскости. Если является точкой шестиугольника, то решетка порождается векторами перемещения АВ и АС, где В и С являются две вершины, которые не являются соседями A, а не напротив. Действительно, на втором рисунке показано, как шестиугольник эквивалентен параллелограмму, полученному путем смещения двух треугольников, отрезанных отрезками AB и AC. Также хорошо на первом рисунке показан другой способ сопоставления мозаики параллелограммами с шестиугольной мозаикой. Если центр шестиугольника равен 0 и вершины по порядку - a, b, c, - a, - b и - c, то Λ - абелева группа с образующими a + b и b + c.
Существует ровно четыре топологии, которые можно создать, определяя стороны параллелограмма разными способами (ниже изображены квадратами):
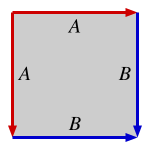 Сфера Сфера |  Реальная проективная плоскость Реальная проективная плоскость |  Бутылка Клейна Бутылка Клейна | 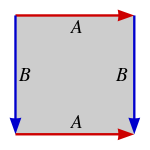 Тор Тор |
Теорема Федорова, установленная русским кристаллографом Евграфом Федоровым в 1891 году, утверждает, что параллелограммы и центрально-симметричные шестиугольники - единственные выпуклые многоугольники, которые являются фундаментальными областями. Есть несколько доказательств этого, некоторые из самых последних связаны с результатами в теории выпуклости, геометрии чисел и упаковки кругов, таких как неравенство Брунна – Минковского. Здесь будут представлены два элементарных доказательства, принадлежащих HSM Coxeter и Voronoi.
Доказательство Кокстера основывается на предположении, что существует центрально-симметричный выпуклый многоугольник C со сторонами 2 m. Затем большой замкнутый параллелограмм, образованный из N 2 фундаментальных параллелограммов, укладывается сдвигами C, выходящими за края большого параллелограмма. Это индуцирует тайлинг на торе C / N Λ. Пусть v, e и f - количество вершин, ребер и граней в этом мозаике (с учетом отождествлений в фактор-пространстве). Тогда, поскольку характеристика Эйлера – Пуанкаре тора равна нулю,
С другой стороны, поскольку каждая вершина находится как минимум на 3 разных ребрах и каждое ребро находится между двумя вершинами,
Более того, поскольку каждое ребро находится ровно на двух гранях,
Следовательно
так что
как требуется.
Доказательство Вороного начинается с наблюдения, что каждое ребро C соответствует элементу x из Λ. Фактически ребро - это ортогональная биссектриса радиуса от 0 до x. Следовательно, основание перпендикуляра от 0 к каждому ребру лежит внутри каждого ребра. Если y - любая точка решетки, то 1/2 y не может лежать в C ; ибо в этом случае –1/2 y также будет лежать в C, что противоречит тому, что C является фундаментальной областью для Λ. Пусть ± х 1,..., ± х м быть 2 м различных точек Λ, соответствующих сторон С. Зафиксируем образующие a и b оператора Λ. Таким образом, x i = α i a + β i b, где α i и β i - целые числа. Невозможно, чтобы оба α i и β i были четными, поскольку в противном случае ± 1/2 x i было бы точкой Λ на стороне, что противоречит тому, что C является фундаментальной областью. Таким образом, есть три возможности для пары целых чисел (α i, β i) по модулю 2: (0,1), (1,0) и (1,1). Следовательно, если m gt; 3, были бы x i и x j с i ≠ j с четными обеими координатами x i - x j, т.е. 1/2 ( x i + x j) лежит в Λ. Но это середина отрезка, соединяющего две внутренние точки ребер, и, следовательно, лежит в C, внутренней части многоугольника. Это снова противоречит тому факту, что C - фундаментальная область. Итак, как утверждается, reductio ad absurdum m ≤ 3.
Для решетки Л в C = R 2, фундаментальная область может быть определена с помощью канонического конформной структуры C. Обратите внимание, что группа конформных преобразований C задается комплексными аффинными преобразованиями g ( z) = az + b с a 0. Эти преобразования сохраняют евклидову метрику d ( z, w) = | z - w | с точностью до фактора, а также с сохранением ориентации. Это подгруппа группы Мёбиуса, фиксирующая точку в ∞. Метрическая структура может использоваться для определения канонической фундаментальной области как C = { z: d ( z, 0) lt; d ( z, λ) для всех λ ≠ 0 в Λ}. (Из определения очевидно, что это фундаментальная область.) Это пример области Дирихле или диаграммы Вороного : поскольку комплексные сдвиги образуют абелеву группу, поэтому коммутируют с действием Λ, эти понятия совпадают. Каноническая фундаментальная область для Λ = Z + Z ω с Im ω gt; 0 является либо симметричным выпуклым параллелограммом, либо шестиугольником с центром 0. В силу конформной эквивалентности период ω может быть дополнительно ограничен, чтобы удовлетворить | Re ω | ≤ 1/2 и | ω | ≥ 1. Как показал Дирихле («Теорема Дирихле о шестиугольнике», 1850 г.), почти для всех ω фундаментальная область представляет собой шестиугольник. При Re ω gt; 0 середины сторон равны ± 1/2, ± ω / 2 и ± ( ω - 1) / 2 ; стороны делят пополам соответствующие радиусы от 0 ортогонально, что полностью определяет вершины. Фактически первая вершина должна иметь вид (1 + ix) / 2 и ω (1 + iy) / 2 с действительными x и y ; так что если ω = a + ib, то a - by = 1 и x = b + ay. Следовательно, y = ( a - 1) / b и x = ( a 2 + b 2 - a) / b. Следовательно, шесть вершин равны ± ω (1 - iy) / 2 и ± (1 ± ix) / 2.
Каждая компактная риманова поверхность X имеет универсальное покрытие поверхности, которое является односвязной римановой поверхности X. Фундаментальная группа из X действует как скольжения из X и может быть идентифицирована с подгруппой Г группы биголоморфизмов из X. Группа Γ, таким образом, действует свободно на X с компактным фактор - пространство Х / Г, который может быть идентифицирован с X. Таким образом, классификация компактных римановых поверхностей сводится к изучению возможных групп Γ. По теореме об униформизации X - это либо сфера Римана, комплексная плоскость, либо единичный круг / верхняя полуплоскость. Первым важным инвариантом компактной римановой поверхности является ее род, топологический инвариант, задаваемый половиной ранга абелевой группы Γ / [Γ, Γ] (которую можно отождествить с группой гомологий H 1 ( X, Z)). Род равен нулю, если накрывающим является сфера Римана; один, если это комплексная плоскость; и больше единицы, если это единичный диск или верхняя полуплоскость.
Бигомоломорфизмы сферы Римана - это просто комплексные преобразования Мёбиуса, и каждое неединичное преобразование имеет по крайней мере одну неподвижную точку, поскольку соответствующая комплексная матрица всегда имеет по крайней мере один ненулевой собственный вектор. Таким образом, если X - сфера Римана, то X должно быть односвязным и биголоморфным сфере Римана, римановой поверхности нулевого рода. Когда X - комплексная плоскость, группа биголоморфизмов является аффинной группой, а комплексные преобразования Мёбиуса фиксируют ∞, поэтому преобразования g ( z) = az + b с a ≠ 0. Неединичные преобразования без неподвижных точек - это как раз те, у которых a = 1 и b ≠ 0, то есть ненулевые трансляции. Таким образом, группа Γ может быть отождествлена с решеткой Λ в C и X с фактором C / Λ, как описано в разделе о фундаментальных многоугольниках первого рода. В третьем случае, когда X - единичный круг или верхняя полуплоскость, группа биголоморфизмов состоит из комплексных преобразований Мёбиуса, фиксирующих единичную окружность или действительную ось. В первом случае преобразования соответствуют элементам группы SU (1, 1) / {± I }; в последнем случае они соответствуют действительным преобразованиям Мёбиуса, поэтому элементы SL (2, R) / {± I }.
Изучение и классификация возможных групп Γ, которые свободно действуют на единичном круге или верхней полуплоскости с компактным фактором - фуксовых групп первого рода - могут быть выполнены путем изучения их фундаментальных многоугольников, как описано ниже. Как заметил Пуанкаре, каждый такой многоугольник обладает особыми свойствами, а именно выпуклостью и естественным спариванием сторон. Они не только позволяют восстановить группу, но и обеспечивают явное представление группы с помощью генераторов и отношений. Наоборот, Пуанкаре доказал, что любой такой многоугольник порождает компактную риманову поверхность; фактически, теорема Пуанкаре о многоугольниках применялась к многоугольникам более общего вида, где многоугольник мог иметь идеальные вершины, но его доказательство было полным только в компактном случае, без таких вершин. Без предположений о выпуклости многоугольника, полные доказательства были даны Маскитом и де Рамом, основанные на идее Сигеля, и их можно найти у Бирдона (1983), Иверсена (1992) и Стиллвелла (1992). Каратеодори дал элементарную трактовку существования мозаики треугольниками Шварца, то есть мозаики геодезическими треугольниками с углами π / a, π / b, π / c с суммой меньше π, где a, b, c - целые числа. Когда все углы равны π / 2 g, это устанавливает замощение правильными 4g- сторонними гиперболическими многоугольниками и, следовательно, существование определенной компактной римановой поверхности рода g как фактор-пространства. Этот специальный пример, который имеет циклическую группу Z 2 g бигомоломорфных симметрий, используется в дальнейшем развитии.
Из классификации с точностью до гомеоморфизма и диффеоморфизма компактных римановых поверхностей следует классификация замкнутых ориентируемых 2-многообразий с точностью до гомеоморфизма и диффеоморфизма: любые два 2-многообразия одного рода диффеоморфны. Фактически, используя разбиение единицы, каждое замкнутое ориентируемое двумерное многообразие допускает риманову метрику. Для компактной римановой поверхности можно также ввести конформную метрику, которая является конформной, так что в голоморфных координатах метрика принимает вид ρ ( z) | dz | 2. Как только эта метрика выбрана, локально биголоморфные отображения являются в точности сохраняющими ориентацию диффеоморфизмами, которые являются конформными, т. Е. Масштабируют метрику гладкой функцией. Существование изотермических координат, которое может быть доказано с помощью либо локальных теорем существования лапласиана, либо уравнения Бельтрами, показывает, что каждому замкнутому ориентированному двумерному риманову многообразию может быть придана комплексная структура, совместимая с его метрикой, и, следовательно, оно имеет структуру компактная риманова поверхность. Эта конструкция показывает, что классификация замкнутых ориентируемых 2-многообразий с точностью до диффеоморфизма или гомеоморфизма сводится к случаю компактных римановых поверхностей.
Классификация с точностью до гомеоморфизма и диффеоморфизма компактных римановых поверхностей может быть выполнена с использованием фундаментального многоугольника. Действительно, как заметил Пуанкаре, выпуклые фундаментальные многоугольники для компактных римановых поверхностей H / Γ могут быть построены путем адаптации метода Дирихле из евклидова пространства к гиперболическому пространству. Затем, следуя Неванлинне и Йосту, фундаментальную область можно поэтапно модифицировать, чтобы получить невыпуклый многоугольник с вершинами, лежащими в одной орбите Γ, и кусочно-геодезическими сторонами. Отношение спаривания на сторонах также изменяется на каждом из этих шагов. Каждый шаг включает разрезание многоугольника диагональным геодезическим сегментом внутри многоугольника и повторную сборку многоугольника с помощью одного из преобразований Мёбиуса, участвующих в формировании пары. Никакие две парные стороны не могут иметь общую вершину в конечном соотношении спаривания, которое удовлетворяет свойствам, аналогичным исходному отношению. Этот многоугольник, в свою очередь, может быть последовательно модифицирован путем повторной сборки многоугольника после разрезания его на диагональный кусочно-геодезический сегмент внутри. Последний многоугольник имеет 4 g эквивалентных вершин со сторонами, которые являются кусочно-геодезическими. Стороны помечены элементами группы, которые задают преобразование Мёбиуса для парной стороны. Чтобы маркировка была
так что Γ порождается a i и b i, подчиняющимся единственному соотношению

Род нулевой поверхности (сфера)

Род один поверхность (тор)

Поверхность рода два

Род три поверхности
Используя теорию чисел пересечений, следует, что форма, полученная путем соединения вершин геодезическими, также является правильным многоугольником, не обязательно выпуклым, и также является фундаментальной областью с теми же элементами группы, которые образуют пары. Это дает фундаментальный многоугольник с ребрами, заданными геодезическими сегментами, и со стандартной разметкой. Абелианизация группы Γ, фактор-группа Γ / [Γ, Γ], является свободной абелевой группой с 2g образующими. Таким образом, род g является топологическим инвариантом. Легко видеть, что две поверхностей с Римана те же родов гомеоморфны так, как топологическое пространство, так как они получены путем идентификации сторон 4 г односторонний многоугольника-евклидовой многоугольника в модели Клейна их диффеоморфизмов между парными сторонами. Применяя эту конструкцию к обычной 4 г односторонний многоугольника позволяет риманова поверхность следует рассматривать как топологический пончик с г отверстиями, стандартным описанием ориентированных поверхностей в вводных текстах по топологии.
Есть еще несколько результатов:
Эти результаты связаны с взаимосвязью между гомеоморфизмами и фундаментальной группой: это отражает тот факт, что группа классов отображений римановой поверхности - группа квазиконформных самогомоморфизмов римановой поверхности H / Γ по модулю гомотопных тождеству - можно отождествить с группой внешних автоморфизмов группы Γ ( теорема Дена – Нильсена – Бэра ). Чтобы увидеть эту связь, заметим, что если f - квазиконформный гомеоморфизм X 1 = H / Γ 1 на X 2 = H / Γ 2, то f поднимается до квазиконформного гомеоморфизма f группы H на себя. Этот подъем уникален с точностью до предкомпозиции с элементами Γ 1 и посткомпозиции с элементами Γ 2. Если π i - проекция H на X i, то f ∘ π 1 = π 2 ∘ f и Γ i - это просто группа гомеоморфизмов g группы H таких, что π i ∘ g = π i. Если следует, что f g = θ ( g) f для g в Γ 1, где θ - групповой изоморфизм Γ 1 на Γ 2. Другой выбор f меняет θ на композицию с внутренним автоморфизмом: такие изоморфизмы называются эквивалентными.
Два изоморфизма θ и θ ′ эквивалентны тогда и только тогда, когда соответствующие гомеоморфизмы f и f ' гомотопны. Фактически достаточно показать, что квазиконформный самогомеоморфизм f поверхности индуцирует внутренний автоморфизм фундаментальной группы тогда и только тогда, когда он гомотопен тождественному отображению: другими словами, гомоморфизм квазиконформной группы самогомеоморфизмов H / Γ в Out Γ переходит в группу классов отображений, на которой он инъективен. В самом деле, предположим сначала, что F ( t) - непрерывный путь самогомеоморфизмов с F (0) = id и F (1) = f. Тогда существует непрерывный подъем F ( t) с F (0) = id. Более того, для каждого g в Γ, F ( t) ∘ g ∘ F ( t) −1 является непрерывно меняющимся элементом Γ, равным g при t = 0 ; поэтому дискретность Γ заставляет этот элемент быть постоянным и, следовательно, равным g, так что F ( t) коммутирует с Γ, поэтому F (1) индуцирует тривиальный автоморфизм. Если, с другой стороны, F - квазиконформный подъем f, индуцирующий внутренний автоморфизм Γ, после композиции с элементом Γ, если необходимо, можно считать, что F коммутирует с Γ. Поскольку F квазиконформен, он продолжается до квазисимметричного гомеоморфизма окружности, который также коммутирует с Γ. Каждый г ≠ ID в Г гиперболической поэтому имеет две фиксированные точки на окружности ± такое, что для всех остальных точек г, г ±п ( г) стремится к более ± как п стремится к бесконечности. Следовательно, F должен зафиксировать эти точки; поскольку эти точки плотны в окружности при изменении g, следует, что F фиксирует единичную окружность. Пусть μ = F z / F z, так что μ - Γ-инвариантный дифференциал Бельтрами. Пусть F ( t) - решение уравнения Бельтрами tμ, нормированное на фиксированные три точки на единичной окружности. Тогда F ( t) коммутирует с Γ и, значит, как и при F = F (1), является единицей на единичной окружности. По построению F ( т) изотопия между идентичностью и F. Это доказывает приемистость.
Доказательство сюръективности основывается на сравнении гиперболической метрики на D с метрикой длины слова на Γ. Предполагая, что с вне ограничения общности, что 0 лежит внутри выпуклого многоугольника фундаментального С и г является элементом Г, луч от 0 до г (0) -The гиперболической геодезическим-проходит через последовательность сдвигов C. Каждый из них получается из предыдущего путем применения генератора Γ или фиксированного произведения образующих (если последовательные переводы пересекаются в вершине). Отсюда следует, что гиперболическое расстояние между 0 и g (0) меньше, чем 4 g, умноженное на длину слова g плюс удвоенный диаметр основного многоугольника. Таким образом, метрика на Γ d 1 ( g, h) = L ( h −1g), определяемая длиной слова L ( g), удовлетворяет
для положительных постоянных a и b. Наоборот, существуют положительные постоянные c и d такие, что
Для данной точки в верхней полуплоскости H и дискретной подгруппы Γ в PSL (2, R), которая действует свободно разрывно на верхней полуплоскости, то можно определить многоугольник Дирихле как множество точек
Здесь d - гиперболическая метрика на верхней полуплоскости. Метрический фундаментальный многоугольник чаще называют многоугольником Дирихле.
В этом разделе, начиная с произвольного многоугольника Дирихле, будет дано описание метода Неванлинны (1955), разработанного Йостом (2002), для преобразования многоугольника в невыпуклый многоугольник с эквивалентными вершинами 4 г и каноническим спаривание по бокам. Этот подход является аналитическим аналогом классической топологической классификации ориентируемых двумерных многогранников, представленной в Seifert amp; Threlfall (1934). Ошибка harvtxt: нет цели: CITEREFNevanlinna1955 ( помощь )
Учитывая риманову поверхность рода g больше единицы, Фрике описал другой фундаментальный многоугольник, канонический многоугольник Фрике, который является очень частным примером многоугольника Дирихле. Многоугольник связан со стандартным представлением основной группы поверхности. Оригинальная конструкция Фрике сложна и описана в Fricke amp; Klein (1897). Используя теорию квазиконформных отображений из Альфорса и Берса, Кины (1965) дал новый, более короткий и более точный вариант конструкции Фрик. Канонический многоугольник Фрике обладает следующими свойствами:
Приведенной выше конструкции достаточно, чтобы гарантировать, что каждая сторона многоугольника является замкнутой (нетривиальной) петлей на римановой поверхности H / Γ. Таким образом, каждая сторона может быть элементом основной группы. В частности, фундаментальная группа имеет 2 g образующих с ровно одним определяющим ограничением:
Род римановой поверхности H / Γ равен g.
Площадь стандартного фундаментального многоугольника - это где g - род римановой поверхности (эквивалентно, где 4 g - количество сторон многоугольника). Поскольку стандартный многоугольник является представителем H / Γ, общая площадь римановой поверхности равна площади стандартного многоугольника. Формула площади следует из теоремы Гаусса – Бонне и в определенном смысле обобщается с помощью формулы Римана – Гурвица.
Явные выражения могут быть предоставлены для регулярного стандарта 4 г односторонний многоугольника, с вращательной симметрией. В этом случае, для римановых поверхностей рода с g- кратной вращательной симметрией, группа может быть задана образующими. Эти генераторы задаются следующими дробно-линейными преобразованиями, действующими в верхней полуплоскости :
для. Параметры представлены как
и
и
Можно проверить, что эти генераторы подчиняются ограничению
что дает полную картину группы.