Биголоморфизм

редактировать

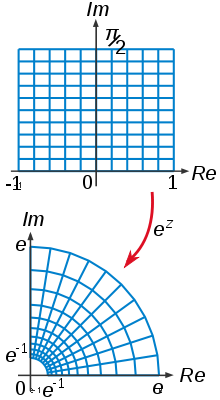
Комплексная экспоненциальная функция биголоморфно отображает прямоугольник на четверть- кольцо.

В математической теории функций одной или более сложных переменных, а также в сложной алгебраической геометрии, биголоморфизм или биголом орфическая функция является биективной голоморфной функцией, обратная которой также голоморфна.

Содержание

1 Формальное определение
2 Теорема Римана об отображении и обобщения
3 Альтернативные определения
4 Ссылки

Формальное определение

Формально биголоморфная функция - это функция $ϕ {\ displaystyle \ phi}$ $\ phi$ определено на открытом подмножестве U $n {\ displaystyle n}$ $n$ -мерного комплексного пространства C со значениями в C, который голоморфен и взаимно однозначно, так что его изображение является открытым множеством $V {\ displaystyle V}$ $V$ в C и обратное $ϕ - 1: V → U {\ displaystyle \ phi ^ {- 1}: V \ to U}$ $\ phi ^ {{- 1}}: V \ в U$ также является голоморфный. В более общем смысле U и V могут быть комплексными многообразиями. Как и в случае функций одной комплексной переменной, достаточным условием для того, чтобы голоморфное отображение было биголоморфным своему образу, является то, что отображение является инъективным, и в этом случае обратное также голоморфно (например, см. Ганнинг 1990, теорема I. 11).

Если существует биголоморфизм $ϕ: U → V {\ displaystyle \ phi \ двоеточие U \ to V}$ $\ phi \ двоеточие U \ в V$ , мы говорим, что U и V биголоморфно эквивалентны или что они биголоморфны .

теорема Римана об отображении и обобщения

Если $n = 1, {\ displaystyle n = 1,}$ $n=1,$ каждые односвязное открытое множество, отличное от всей комплексной плоскости, биголоморфно единичному кругу (это теорема об отображении Римана ). В высших измерениях ситуация совсем иная. Например, открытые единичные шары и открытые единичные полидиски не являются биголоморфно эквивалентными для $n>1. {\ displaystyle n>1.}$ $n>1.$ На самом деле не существует даже правильной голоморфной функции от одного к другому.

Альтернативные определения

В случае карт f: U → C, определенный на открытом подмножестве U комплексной плоскости C, некоторые авторы (например, Freitag 2009, определение IV.4.1) определяют конформное отображение быть инъективным отображением с ненулевой производной, т. Е. F '(z) ≠ 0 для любого z в U. Согласно этому определению отображение f: U → C конформно тогда и только тогда, когда f : U → f (U) является биголоморфным. Другие авторы (например, Conway 1978) определяют конформное отображение как отображение с ненулевой производной, не требуя, чтобы отображение было инъективным. Согласно этому более слабому определению конформности, конформное отображение не обязательно биголоморфна, даже если она локально биголоморфна. Например, если f: U → U определяется как f (z) = z с U = C - {0}, то f конформна на U, поскольку ее производная f ’(z) = 2z ≠ 0, но не биголоморфна, поскольку она равна 2-1.

Ссылки

Джон Б. Конвей (1978). Функции одной комплексной переменной. Springer-Verlag. ISBN 3-540-90328-3.
Джон П. Д'Анджело (1993). Несколько комплексных переменных и геометрия реальных гиперповерхностей. CRC Press. ISBN 0-8493-8272-6.
Эберхард Фрайтаг и Рольф Бусам (2009). Комплексный анализ. Springer-Verlag. ISBN 978-3-540-93982-5.
Роберт С. Ганнинг (1990). Введение в голоморфные функции многих переменных, Vol. II. Уодсворт. ISBN 0-534-13309-6.
Стивен Г. Кранц (2002). Теория функций нескольких комплексных переменных. Американское математическое общество. ISBN 0-8218-2724-3.

. Эта статья включает в себя материал из биоголоморфного эквивалента на PlanetMath, который находится под лицензией Creative Commons Attribution / Share- Аналогичная лицензия.