Динамика полета (самолет с неподвижным крылом)

Наука об ориентации и управлении летательным аппаратом в трех измерениях

Динамика полета - это наука ориентации и управления транспортным средством в воздухе в трех измерениях. Три критических параметра динамики полета - это углы поворота в трех измерениях относительно центра тяжести (cg) транспортного средства, известные как тангаж, крен и рыскание.

Системы управления регулируют ориентацию автомобиля относительно его центра тяжести. Система управления включает в себя управляющие поверхности, которые при отклонении создают момент (или пару от элеронов) вокруг ЦТ, который вращает самолет по тангажу, крену и рысканью. Например, момент тангажа возникает из-за силы, приложенной на расстоянии вперед или назад от cg, заставляя летательный аппарат наклоняться вверх или вниз.

Крен, тангаж и рыскание относятся к поворотам вокруг соответствующих осей, начиная с определенного состояния равновесия установившегося полета. Угол равновесного крена известен как уровень крыльев или нулевой угол крена.

Наиболее распространенное авиационное соглашение определяет крен как действие относительно продольной оси, положительное при опущенном правом (правом) крыле. Рыскание относительно вертикальной оси корпуса положительно, носом вправо. Шаг - это ось, перпендикулярная продольной плоскости симметрии, положительный нос вверх.

A самолет с неподвижным крылом увеличивает или уменьшает подъемную силу, создаваемую крыльями, когда он наклоняет нос вверх или вниз, увеличивая или уменьшая угол атаки (AOA). Угол крена также известен как угол крена на самолете с неподвижным крылом, который обычно «крен», чтобы изменить горизонтальное направление полета. Самолет имеет обтекаемую форму от носа до хвоста для уменьшения лобового сопротивления, что позволяет поддерживать угол бокового скольжения близким к нулю, хотя самолет может быть намеренно «смещен в сторону» для увеличения лобового сопротивления и скорости снижения во время при посадке, чтобы самолет оставался таким же, как курс ВПП во время посадки с боковым ветром и во время полета с асимметричной мощностью.

рыскание тангаж крен рыскание или определение угла курса тангаж определение угла 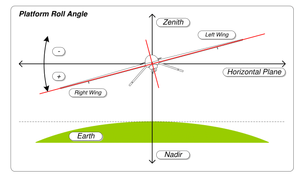определение угла крена

• 1 Введение
  • 1.1 Системы отсчета
  • 1.2 Расчетные случаи
• 2 Силы полета
  • 2.1 Аэродинамическая сила
    • 2.1.1 Компоненты аэродинамической силы
    • 2.1.2 Аэродинамические коэффициенты
    • 2.1.3 Безразмерные параметры и аэродинамические режимы
    • 2.1.4 Уравнение коэффициента сопротивления и аэродинамический КПД
    • 2.1.5 Параболический и общий коэффициент сопротивления
    • 2.1.6 Изменение параметров с числом Маха
    • 2.1.7 Аэродинамическая сила в заданной атмосфере
• 3 Статическая устойчивость и выдержка trol
  • 3.1 Продольная статическая устойчивость
  • 3.2 Направленная устойчивость
• 4 Динамическая устойчивость и управляемость
  • 4.1 Продольные моды
    • 4.1.1 Короткопериодические колебания шага
    • 4.1.2 Фугоид
  • 4.2 Боковые режимы
    • 4.2.1 Голландский крен
    • 4.2.2 Производные поперечной и продольной устойчивости
    • 4.2.3 Уравнения движения
    • 4.2.4 Оседание крена
    • 4.2.5 Спиральный режим
      • 4.2.5.1 Траектория спирального режима
• 5 См. Также
• 6 Ссылки
  • 6.1 Примечания
  • 6.2 Библиография
• 7 Внешние ссылки

Справочные рамки

Три правосторонних, декартовых систем координат часто используются в динамике полета. Первая система координат имеет начало координат, зафиксированное в системе отсчета Земли:

• Кадр Земли
  • Начало координат - произвольное, фиксированное относительно поверхности Земли
  • xEось - положительное в направлении север
  • yEось - положительно в направлении оси восток
  • zE- положительно по направлению к центру Земли

Во многих приложениях динамики полета предполагается, что система отсчета Земли инерциальна с плоским x E,yE-плоскость, хотя земная рамка также может рассматриваться как сферическая система координат с началом в центре Земли.

Две другие системы отсчета закреплены на теле, их исходные точки перемещаются вместе с летательным аппаратом, обычно в центре тяжести. Для самолета, симметричного справа налево, рамы могут быть определены как:

• рама корпуса
  • Начало координат - центр тяжести самолета;
  • xbось - положительно от носа самолета в плоскость симметрии самолета
  • zb, ось - перпендикулярна оси x b, в плоскости симметрии самолета, положительна ниже оси самолета
  • yb- перпендикулярна оси x b,zb-плоскость, положительная, определяется по правилу правой руки (обычно положительно вне правого крыла)
• Система ветра
  • Начало координат - центр тяжести самолета
  • xwось - положительная направление вектора скорости ЛА относительно воздушной оси
  • zw- перпендикулярно оси x w, в плоскости симметрии ЛА, положительное ниже оси
  • ywЛА - перпендикулярно к плоскости x w,zw, положительно определяется правилом правой руки (обычно положительно справа)

Асимметричные самолеты имеют аналогичные неподвижные корпуса, но для выбора должны использоваться другие соглашения укажите точное направление осей x и z.

Кадр Земли - удобный кадр для выражения поступательной и вращательной кинематики самолета. Кадр Земли также полезен тем, что при определенных предположениях он может быть аппроксимирован инерционным. Кроме того, одна сила, действующая на самолет, - вес, - фиксируется в направлении + z E.

Каркас корпуса часто представляет интерес, потому что начало координат и оси остаются фиксированными относительно самолета. Это означает, что относительная ориентация кадров Земли и тела описывает положение самолета. Кроме того, направление силы тяги обычно фиксируется в раме корпуса, хотя некоторые самолеты могут изменять это направление, например, с помощью вектора тяги.

Ветровая рама представляет собой удобную раму для выражения аэродинамических сил и моментов. действуя на самолете. В частности, чистая аэродинамическая сила может быть разделена на составляющие вдоль осей ветровой рамы, с силой сопротивления в направлении -x w и подъемная сила в направлении -z w.

Мнемоника для запоминания названий углов

В дополнение к определению опорных кадров может быть определена относительная ориентация опорных кадров. Относительная ориентация может быть выражена в различных формах, в том числе:

• Матрицы вращения
• Направляющие косинусы
• Углы Эйлера
• Кватернионы

Различные углы Эйлера, относящиеся к трем системам отсчета, важны для динамики полета. Существует много соглашений об углах Эйлера, но все последовательности поворота, представленные ниже, используют соглашение z-y'-x ". Это соглашение соответствует типу углов Тейта-Брайана, которые обычно называют Это соглашение подробно описывается ниже для углов Эйлера крена, тангажа и рыскания, которые описывают ориентацию корпуса тела по отношению к кадру Земли. Другие наборы углов Эйлера описаны ниже по аналогии.

К преобразовать из кадра Земли в корпус тела с помощью углов Эйлера, следующие повороты выполняются в предписанном порядке. Сначала поверните оси системы координат Земли x E и y E вокруг оси z E на угол рыскания ψ. В результате получается промежуточная система отсчета с осями, обозначенными x ', y', z ', где z' = z E. Во-вторых, поверните Оси x 'и z' вокруг оси y 'на угол наклона θ. Это приводит к другой промежуточной системе отсчета с осями, обозначенными x ", y", z ", где y" = y'. Наконец, поверните y "и z " оси вокруг оси x "на угол крена φ. Опорная рамка, которая получается после трех вращений, - это рамка тела.

На основе приведенных выше соглашений о вращениях и осях, угол рыскания ψ - это угол между севером и проекцией продольной оси самолета на горизонтальную плоскость, угол тангажа θ - это угол между продольной осью самолета и по горизонтали, а угол крена φ представляет собой вращение вокруг продольной оси самолета после поворота по рысканью и тангажу.

Для преобразования из системы координат Земли в систему координат ветра три угла Эйлера - это угол крена μ, угол траектории полета γ и угол курса σ. При выполнении поворотов, описанных выше, для получения кадра ветра из кадра Земли, (μ, γ, σ) аналогичны (φ, θ, ψ) соответственно. Курсовой угол σ - это угол между севером и горизонтальной составляющей вектора скорости, который описывает, в каком направлении летательный аппарат движется относительно сторон света. Угол траектории полета γ - это угол между горизонталью и вектором скорости, который описывает, набирает ли самолет или спускается. Угол крена μ представляет собой вращение подъемной силы вокруг вектора скорости, что может указывать на то, разворачивается ли самолет.

. Для перехода от системы ветра к корпусу два угла Эйлера равны угол атаки α и угол бокового скольжения β. При выполнении вращений, описанных ранее, чтобы получить раму тела из ветровой рамы, (α, β) аналогичны (θ, ψ), соответственно; угол, аналогичный φ в этом преобразовании, всегда равен нулю. Угол β бокового скольжения представляет собой угол между вектором скорости и проекцией продольной оси летательного аппарата на плоскость x w,yw, который описывает, есть ли поперечный компонент скорости летательного аппарата, также известный как боковое скольжение. Угол атаки α представляет собой угол между плоскостью x w,ywи продольной осью летательного аппарата и, среди прочего, является важной переменной при определении величины подъемной силы.

Расчетные случаи

При анализе устойчивости самолета обычно учитывают возмущения относительно номинального устойчивого состояния полета. Таким образом, анализ может быть применен, например, в предположении:

Прямой и горизонтальный полет

Поворот с постоянной скоростью

Подход и посадка

Взлет

Скорость, высота и Триммерный угол атаки различен для каждого условия полета, кроме того, самолет будет по-разному настроен, например на малой скорости закрылки могут быть раскрыты, а шасси может быть опущено.

За исключением (или при значительном боковом скольжении), продольные уравнения движения (включая тангаж и подъемную силу) могут рассматриваться независимо от бокового движения (включая крен и рыскание).

Далее рассматриваются возмущения относительно номинальной прямой и горизонтальной траектории полета.

Для упрощения анализа (относительно) предполагается, что управляющие поверхности фиксируются на протяжении всего движения, это устойчивость с фиксацией ручки. Анализ без прилипания требует дальнейшего усложнения учета движения рулевых поверхностей.

Кроме того, предполагается, что полет происходит в неподвижном воздухе, и самолет рассматривается как твердое тело.

Три силы действуют на самолет в полет: вес, тяга и аэродинамическая сила.

Аэродинамическая сила

Составляющие аэродинамической силы

Выражение для вычислить аэродинамическую силу:

$FA\; =\; \int \; \Sigma \; (-\; \Delta \; pn\; +\; f)\; d\; \sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{A\}\; =\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; (-\; \backslash \; Delta\; p\; \backslash \; mathbf\; \{\; n\}\; +\; \backslash \; mathbf\; \{f\})\; \backslash ,\; d\; \backslash \; sigma\}$

где:

$\Delta \; p\; \equiv \; \{\backslash \; displaystyle\; \backslash \; Delta\; p\; \backslash \; Equiv\}$Разница между статическим давлением и свободным текущим давлением

$n\; \equiv \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{n\}\; \backslash \; Equiv\}$вектор внешней нормали элемента области

$f\; \equiv \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{f\}\; \backslash \; Equiv\}$вектор касательного напряжения, применяемый воздухом к телу

$\Sigma \; \equiv \; \{\backslash \; displaystyle\; \backslash \; Sigma\; \backslash \; Equiv\}$адекватная опорная поверхность

, спроецированная на оси ветра, получаем:

$FA\; =\; -\; (\; iw\; D\; +\; jw\; Q\; +\; квт\; L)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{A\}\; =\; -\; (\backslash \; mathbf\; \{i\}\; \_\; \{w\}\; D\; +\; \backslash \; mathbf\; \{j\}\; \_\; \{w\}\; Q\; +\; \backslash \; mathbf\; \{k\}\; \_\; \{w\}\; L)\}$

где:

$D\; \equiv \; \{\backslash \; displaystyle\; D\; \backslash \; Equiv\}$Drag

$Q\; \equiv \; \{\backslash \; displaystyle\; Q\; \backslash \; Equiv\}$Боковое усилие

$L\; \equiv \; \{\backslash \; displaystyle\; L\; \backslash \; Equiv\}$Lift

Аэродинамические коэффициенты

Динамическое давление свободного течения $\equiv \; q\; =\; 1\; 2\; \rho \; V\; 2\; \{\backslash \; displaystyle\; \backslash \; Equiv\; q\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash ,\; \backslash \; rho\; \backslash ,\; V\; ^\; \{2\}\}$

Правильная ссылка поверхность (поверхность крыла, в случае плоскости ) $\equiv \; S\; \{\backslash \; Displaystyle\; \backslash \; Equiv\; S\}$

Коэффициент давления $\equiv \; C\; p\; =\; p\; -\; p\; \infty \; q\; \{\backslash \; displaystyle\; \backslash \; Equ\; C\_\; \{p\}\; =\; \{\backslash \; dfrac\; \{p-p\; \_\; \{\backslash \; infty\}\}\; \{q\}\}\}$

Коэффициент трения $\equiv \; C\; f\; =\; fq\; \{\backslash \; displaystyle\; \backslash \; Equiv\; C\_\; \{f\}\; =\; \{\backslash \; dfrac\; \{f\}\; \{q\}\}\; \}$

Коэффициент лобового сопротивления $\equiv \; C\; d\; =\; D\; q\; S\; =\; -\; 1\; S\; \int \; \Sigma \; [(-\; C\; p)\; n\; \bullet \; iw\; +\; C\; ft\; \bullet \; iw]\; d\; \sigma \; \{\backslash \; displaystyle\; \backslash \; Equiv\; C\_\; \{d\; \}\; =\; \{\backslash \; dfrac\; \{D\}\; \{qS\}\}\; =\; -\; \{\backslash \; dfrac\; \{1\}\; \{S\}\}\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; [(-\; C\_\; \{p\})\; \backslash \; mathbf\; \{n\}\; \backslash \; bullet\; \backslash \; mathbf\; \{i\_\; \{w\}\}\; +\; C\_\; \{f\}\; \backslash \; mathbf\; \{t\}\; \backslash \; bullet\; \backslash \; mathbf\; \{i\_\; \{w\}\}]\; \backslash ,\; d\; \backslash \; sigma\}$

Коэффициент поперечной силы $\equiv \; CQ\; =\; Q\; q\; S\; =\; -\; 1\; S\; \int \; \Sigma \; [(-\; C\; p)\; n\; \bullet \; jw\; +\; C\; ft\; \bullet \; jw]\; d\; \sigma \; \{\backslash \; Displaystyle\; \backslash \; Equiv\; C\_\; \{Q\}\; =\; \{\backslash \; dfrac\; \{Q\}\; \{qS\}\}\; =\; -\; \{\backslash \; dfrac\; \{1\}\; \{S\}\}\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; [(-\; C\_\; \{p\})\; \backslash \; mathbf\; \{n\}\; \backslash \; bullet\; \backslash \; mathbf\; \{j\_\; \{w\}\}\; +\; C\_\; \{f\}\; \backslash \; mathbf\; \{t\}\; \backslash \; bullet\; \backslash \; mathbf\; \{j\_\; \{w\}\}]\; \backslash ,\; d\; \backslash \; sigma\}$

Коэффициент подъемной силы $\equiv \; CL\; =\; L\; q\; S\; =\; -\; 1\; S\; \int \; \Sigma \; [(-\; C\; p)\; n\; \bullet \; квт\; +\; C\; ft\; \bullet \; кВт]\; d\; \sigma \; \{\backslash \; Displaystyle\; \backslash \; Equiv\; C\_\; \{L\}\; =\; \{\backslash \; dfrac\; \{L\}\; \{qS\}\}\; =\; -\; \{\backslash \; dfrac\; \{1\}\; \{S\}\}\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; [(-\; C\_\; \{p\})\; \backslash \; mathbf\; \{n\}\; \backslash \; bullet\; \backslash \; mathbf\; \{k\_\; \{w\}\}\; +\; C\_\; \{f\}\; \backslash \; mathbf\; \{\; t\}\; \backslash \; bullet\; \backslash \; mathbf\; \{k\_\; \{w\}\}]\; \backslash ,\; d\; \backslash \; sigma\}$

Необходимо знать C p и C f в каждой точке рассматриваемого поверхность.

Безразмерные параметры и аэродинамические режимы

При отсутствии тепловых эффектов есть три замечательных безразмерных числа:

• Сжимаемость потока:

Число Маха $\equiv \; M\; =\; V\; a\; \{\backslash \; displaystyle\; \backslash \; Equiv\; M\; =\; \{\backslash \; dfrac\; \{V\}\; \{a\}\}\}$

• Вязкость потока:

число Рейнольдса $\equiv \; R\; e\; =\; \rho \; V\; l\; \mu \; \{\; \backslash \; Displaystyle\; \backslash \; Equiv\; Re\; =\; \{\backslash \; dfrac\; \{\backslash \; rho\; Vl\}\; \{\backslash \; mu\}\}\}$

• Редкость потока:

число Кнудсена $\equiv \; K\; n\; =\; \lambda \; l\; \{\backslash \; displaystyle\; \backslash \; Equiv\; Kn\; =\; \{\backslash \; dfrac\; \{\backslash \; lambda\}\; \{l\}\}\}$

где:

$a\; =\; k\; R\; \theta \; \equiv \; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; sqrt\; \{kR\; \backslash \; theta\}\}\; \backslash \; Equiv\}$скорость звука

$k\; \equiv \; \{\backslash \; displaystyle\; k\; \backslash \; Equiv\}$коэффициент теплоемкости

$R\; \equiv \; \{\backslash \; displaystyle\; R\; \backslash \; Equiv\}$газовая постоянная на единицу массы

$\theta \; \equiv \; \{\backslash \; displaystyle\; \backslash \; theta\; \backslash \; Equiv\}$абсолютная температура

$\lambda \; =\; \mu \; \rho \; \pi \; 2\; R\; \theta \; =\; MR\; ek\; \pi \; 2\; \equiv \; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \{\backslash \; dfrac\; \{\backslash \; mu\}\; \{\backslash \; rho\}\}\; \{\backslash \; sqrt\; \{\backslash \; dfrac\; \{\backslash \; pi\}\; \{2R\; \backslash \; theta\}\}\}\; =\; \{\backslash \; dfrac\; \{M\}\; \{Re\}\}\; \{\backslash \; sqrt\; \{\backslash \; dfrac\; \{k\; \backslash \; pi\}\; \{2\}\}\; \}\; \backslash \; Equiv\}$средний свободный пробег

Согласно λ существует три возможных степени разрежения, и соответствующие им движения называются:

• Континуумный ток (незначительное разрежение): $MR\; e\; \ll \; 1\; \{\backslash \; displaystyle\; \{\backslash \; dfrac\; \{M\}\; \{Re\}\}\; \backslash \; ll\; 1\}$
• Переходный ток (умеренное разрежение): $MR\; e\; \approx \; 1\; \{\backslash \; displaystyle\; \{\backslash \; dfrac\; \{M\}\; \{Re\}\}\; \backslash \; приблизительно\; 1\}$
• Свободный молекулярный ток (высокое разрежение): $MR\; e\; \gg \; 1\; \{\backslash \; displaystyle\; \{\backslash \; dfrac\; \{M\}\; \{Re\}\}\; \backslash \; gg\; 1\}$

В динамике полета движение тела в потоке рассматривается как непрерывный ток. Во внешнем слое пространства, окружающего тело вязкость будет незначительной. Однако влияние вязкости необходимо учитывать при анализе потока вблизи пограничного слоя.

В зависимости от сжимаемости потока можно учитывать различные виды токов:

• Несжимаемый дозвуковой ток :
• Сжимаемый дозвуковой ток :
• Трансзвуковой ток :
• Сверхзвуковой ток :
• Гиперзвуковой ток :

Уравнение коэффициента сопротивления и аэродинамика КПД

Если геометрия тела фиксирована и в случае симметричного полета (β = 0 и Q = 0), коэффициенты давления и трения являются функциями, зависящими от:

$C\; p\; =\; C\; p\; (\alpha \; M,\; R\; e,\; P)\; \{\backslash \; Displaystyle\; C\_\; \{p\}\; =\; C\_\; \{p\}\; (\backslash \; alpha,\; M,\; Re,\; P)\}$

$C\; f\; =\; C\; f\; (\alpha ,\; M,\; R\; e,\; P)\; \{\; \backslash \; displaystyle\; C\_\; \{f\}\; =\; C\_\; \{f\}\; (\backslash \; alpha,\; M,\; Re,\; P)\}$

где:

$\alpha \; \equiv \; \{\backslash \; displaystyle\; \backslash \; alpha\; \backslash \; Equiv\}$угол атаки

$P\; \equiv \; \{\backslash \; displaystyle\; P\; \backslash \; Equiv\}$рассматриваемая точка поверхности

В этих условиях сопротивление и коэффициент подъемной силы равны функции зависят исключительно от угла атаки корпуса и Маха и чисел Рейнольдса. Аэродинамическая эффективность, определяемая как соотношение между коэффициентами подъемной силы и сопротивления, также будет зависеть от этих параметров.

$\{CD\; =\; CD\; (\alpha ,\; M,\; R\; e)\; CL\; =\; CL\; (\alpha ,\; M,\; R\; e)\; E\; =\; E\; (\alpha ,\; M,\; R\; e)\; =\; CLCD\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; C\_\; \{\; D\}\; =\; C\_\; \{D\}\; (\backslash \; alpha,\; M,\; Re)\; \backslash \backslash \; C\_\; \{L\}\; =\; C\_\; \{L\}\; (\backslash \; alpha,\; M,\; Re)\; \backslash \backslash \; E\; =\; E\; (\backslash \; alpha,\; M,\; Re)\; =\; \{\backslash \; dfrac\; \{C\_\; \{L\}\}\; \{C\_\; \{D\}\}\}\; \backslash \backslash \backslash \; end\; \{cases\}\}\}$

Также возможно получить зависимость коэффициента сопротивления от коэффициент подъемной силы. Это соотношение известно как уравнение коэффициента сопротивления:

$CD\; =\; CD\; (CL,\; M,\; R\; e)\; \equiv \; \{\backslash \; displaystyle\; C\_\; \{D\}\; =\; C\_\; \{D\}\; (C\_\; \{L\},\; M,\; Re)\; \backslash \; Equiv\}$Уравнение коэффициента сопротивления

Аэродинамическая эффективность имеет максимальное значение, E max, относительно C L, где касательная линия от начала координат касается сопротивления график уравнения коэффициента.

Коэффициент лобового сопротивления C D можно разложить двумя способами. Первое типичное разложение разделяет эффекты давления и трения:

$CD\; =\; CD\; f\; +\; CD\; p\; \{CD\; f\; =\; D\; q\; S\; =\; -\; 1\; S\; \int \; \Sigma \; C\; ft\; \bullet \; iwd\; \sigma \; CD\; p\; =\; D\; q\; S\; =\; -\; 1\; S\; \int \; \Sigma \; (\; -\; C\; p)\; n\; \bullet \; iwd\; \sigma \; \{\backslash \; displaystyle\; C\_\; \{D\}\; =\; C\_\; \{Df\}\; +\; C\_\; \{Dp\}\; \{\backslash \; begin\; \{cases\}\; C\_\; \{Df\}\; =\; \{\backslash \; dfrac\; \{D\}\; \{qS\}\}\; =\; -\; \{\backslash \; dfrac\; \{1\}\; \{S\}\}\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; C\_\; \{f\}\; \backslash \; mathbf\; \{t\}\; \backslash \; bullet\; \backslash \; mathbf\; \{i\_\; \{w\}\}\; \backslash ,\; d\; \backslash \; sigma\; \backslash \backslash \; C\_\; \{Dp\}\; =\; \{\backslash \; dfrac\; \{\; D\}\; \{qS\}\}\; =\; -\; \{\backslash \; dfrac\; \{1\}\; \{S\}\}\; \backslash \; int\; \_\; \{\backslash \; Sigma\}\; (-\; C\_\; \{p\})\; \backslash \; mathbf\; \{n\}\; \backslash \; bullet\; \backslash \; mathbf\; \{i\_\; \{w\}\}\; \backslash ,\; d\; \backslash \; sigma\; \backslash \; end\; \{cases\}\}\}$

Есть второе типичное разложение, учитывающее определение уравнения коэффициента сопротивления. Это разложение разделяет влияние коэффициента подъемной силы в уравнении, получая два члена C D0 и C Di. C D0 известен как коэффициент паразитного сопротивления, и это базовый коэффициент тяги при нулевой подъемной силе. C Di известен как коэффициент индуцированного сопротивления и создается подъемной силой тела.

$CD\; =\; CD\; 0\; +\; CD\; i\; \{CD\; 0\; =\; (CD)\; CL\; =\; 0\; CD\; i\; \{\backslash \; displaystyle\; C\_\; \{D\}\; =\; C\_\; \{D0\}\; +\; C\_\; \{Di\}\; \{\backslash \; begin\; \{cases\}\; C\_\; \{D0\}\; =\; (C\_\; \{D\})\; \_\; \{C\_\; \{L\}\; =\; 0\}\; \backslash \backslash \; C\_\; \{Di\}\; \backslash \; end\; \{cases\}\}\}$

Параболический и общий коэффициент сопротивления

Хорошая попытка определения коэффициента индуцированного сопротивления означает параболическую зависимость подъемной силы

$CD\; i\; =\; k\; CL\; 2\; \Rightarrow \; CD\; =\; CD\; 0\; +\; k\; CL\; 2\; \{\backslash \; displaystyle\; C\_\; \{Di\}\; =\; kC\_\; \{L\}\; ^\; \{2\}\; \backslash \; Rightarrow\; C\_\; \{D\}\; =\; C\_\; \{D0\}\; +\; kC\_\; \{L\}\; ^\; \{2\}\}$

Аэродинамическая эффективность теперь рассчитывается как:

$E\; =\; CLCD\; 0\; +\; k\; CL\; 2\; \Rightarrow \; \{E\; max\; =\; 1\; 2\; k\; CD\; 0\; (CL)\; E\; max\; =\; CD\; 0\; К\; (CD\; i)\; E\; max\; =\; CD\; 0\; \{\backslash \; displaystyle\; E\; =\; \{\backslash \; dfrac\; \{C\_\; \{L\}\}\; \{C\_\; \{D0\}\; +\; kC\_\; \{L\}\; ^\; \{2\}\}\}\; \backslash \; Rightarrow\; \{\backslash \; begin\; \{cases\; \}\; E\_\; \{max\}\; =\; \{\backslash \; dfrac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{kC\_\; \{D0\}\}\}\}\}\; \backslash \backslash \; (C\_\; \{L\})\; \_\; \{Emax\}\; =\; \{\backslash \; sqrt\; \{\backslash \; dfrac\; \{C\_\; \{D0\}\; \}\; \{k\}\}\}\; \backslash \backslash \; (C\_\; \{Di\})\; \_\; \{Emax\}\; =\; C\_\; \{D0\}\; \backslash \; end\; \{cases\}\}\}$

Если конфигурация плоскости симметрична относительно плоскости XY, минимальный коэффициент сопротивления равно паразитному сопротивлению самолета.

$CD\; min\; =\; (CD)\; CL\; =\; 0\; =\; CD\; 0\; \{\backslash \; displaystyle\; C\_\; \{Dmin\}\; =\; (C\_\; \{D\})\; \_\; \{CL\; =\; 0\}\; =\; C\_\; \{D0\}\}$

Если конфигурация асимметрична Однако по отношению к плоскости XY флаг минимума отличается от паразитного сопротивления. В этих случаях можнопроследить новое приближенное уравнение параболического сопротивления, оставив минимальное значение сопротивления при нулевом значении подъемной силы.

$CD\; min\; =\; CDM\; \ne \; (CD)\; CL\; =\; 0\; \{\backslash \; displaystyle\; C\_\; \{Dmin\}\; =\; C\_\; \{DM\}\; \backslash \; neq\; (C\_\; \{D\})\; \_\; \{CL\; =\; 0\}\}$

$CD\; =\; CDM\; +\; k\; (\; CL\; -\; CLM)\; 2\; \{\backslash \; displaystyle\; C\_\; \{D\}\; =\; C\_\; \{DM\}\; +\; k\; (C\_\; \{L\}\; -C\_\; \{LM\})\; ^\; \{2\}\}$

Вариация параметров с числом Маха

Коэффициент давления изменяется с числом Маха в соответствии с приведенным ниже использованием:

$C\; p\; =\; C\; p\; 0\; |\; 1\; -\; M\; \infty \; 2\; |\; \{\backslash \; displaystyle\; C\_\; \{p\}\; =\; \{\backslash \; frac\; \{C\_\; \{p0\}\}\; \{\backslash \; sqrt\; \{|\; 1-\; \{M\; \_\; \{\backslash \; infty\}\}\; ^\; \{2\}\; |\}\}\}\}$

где

• Cp- сжимаемый коэффициент давления
• Cp0- несжимаемый коэффициент давления
• M∞- число Маха набегающего потока.

Это соотношение достаточно точно для 0,3 < M < 0.7 and when M = 1 it becomes ∞ which is impossible physical situation and is called сингулярности Прандтля - Глауэрта.

Аэродинамическая сила в заданной атмосфере

см. Аэродинамическая сила

Продольная статическая устойчивость

см. Продольная статическая устойчивость

Направленная устойчивость

Направленная устойчивость или устойчивость флюгера соответствует с статической устойчивостью самолета относительно оси z. Так же, как и в случае некоторой устойчивости, желательно, чтобы летательный аппарат имел тенденцию возвращаться в равновесие, когда он подвергается некоторому состоянию нарушения рыскания. Для этого наклонного момента рыскания должен быть положительным. Самолет, обладающий таким режимом устойчивости, всегда указывать в сторону относительного ветра, отсюда и название «устойчивость флюгера».

Продольные моды

Обычной практикой является выведение типичного уравнения четвертого порядка для описания продольного движения, а факторизация он примерно в высокочастотном режим и низкочастотный режим. Используемый здесь основан на использовании качественных знаний о поведении воздушного судна для упрощения с помощью самого начала и достижения результата с помощью более доступного маршрута.

Два продольных движения (режим) называются короткопериодными колебаниями основного тона (SPPO) и фугоидом.

короткопериодическими колебаниями основного тона

Короткий ввод (в терминологии систем управления - импульс ) по тангажу (обычно через руль высоты в стандартном самолете с неподвижным крылом), как правило, приводит к перерегулированию относительно состояния дифферента. Переход характеризует затухающим гармоническим движением относительно нового дифферента. Траектория очень мало изменяется за время необходимое, для затухания колебаний.

Обычно это колебание имеет частоту (следовательно, короткий период) и затухает в течение нескольких секунд. Пример из реальной жизни: пилот выбирает новое положение для набора высоты, например, нос на 5 ° вверх от исходного положения. Можно использовать короткое резкое оттягивание рулевой колонки назад, что обычно приводит к колебаниям относительно нового состояния дифферента. Если колебания слабо затухают, самолету потребуется длительный период времени, чтобы прийти в новое состояние, что может привести к колебаниям, вызванным пилотом. Если режим короткого периода нестабилен, пилот, как правило, не может управлять летательным аппаратом в любом периоде времени.

Это затухание гармоническое движение называется короткопериодным колебанием тангажа, оно возникает из-за тенденций стабильного летательного аппарата к точке в целом. направление полета. По своей природе он очень похож на режим флюгера ракетных или ракетных конфигураций. Движение включает, главным образом, высоту тона $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$(theta) и угол падения $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$(alpha). Направление вектора скорости относительно инерциальных осей равно $\theta \; -\; \alpha \; \{\backslash \; displaystyle\; \backslash \; theta\; -\; \backslash \; alpha\}$. Вектор скорости:

$uf\; =\; U\; cos\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; u\_\; \{f\}\; =\; U\; \backslash \; cos\; (\backslash \; theta\; -\; \backslash \; alpha)\}$

$wf\; =\; U\; sin\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; w\_\; \{f\}\; =\; U\; \backslash \; sin\; (\backslash \; theta\; -\; \backslash \; alpha)\}$

где $uf\; \{\backslash \; displaystyle\; u\_\; \{f\}\}$,$wf\; \{\backslash \; displaystyle\; w\_\; \{f\}\}$- компоненты скорости по инерциальной оси. Согласно Второму закону Ньютона, ускорения пропорциональны силам, поэтому силы в инерционных осях равны:

$X\; f\; =\; mdufdt\; =\; md\; U\; dt\; соз\; \; (\theta \; -\; \alpha )\; -\; м\; U\; d\; (\theta \; -\; \alpha )\; dt\; грех\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; X\_\; \{f\}\; =\; m\; \{\backslash \; frac\; \{du\_\; \{f\}\}\; \{dt\}\}\; =\; m\; \{\backslash \; frac\; \{dU\}\; \{\; dt\}\}\; \backslash \; cos\; (\backslash \; theta\; -\; \backslash \; alpha)\; -mU\; \{\backslash \; frac\; \{d\; (\backslash \; theta\; -\; \backslash \; alpha)\}\; \{dt\}\}\; \backslash \; sin\; (\backslash \; theta\; -\; \backslash \; alpha)\}$

$Z\; е\; знак\; равно\; mdwfdt\; =\; мд\; U\; dt\; грех\; \; (\theta \; -\; \alpha )\; +\; m\; U\; d\; (\theta \; -\; \alpha )\; dt\; соз\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; Z\_\; \{f\}\; =\; m\; \{\backslash \; frac\; \{dw\_\; \{f\}\}\; \{dt\}\}\; =\; m\; \{\backslash \; frac\; \{dU\}\; \{dt\}\}\; \backslash \; sin\; (\backslash \; theta\; -\; \backslash \; alpha)\; +\; mU\; \{\backslash \; frac\; \{d\; (\backslash \; theta\; -\; \backslash \; alpha)\}\; \{dt\}\}\; \backslash \; cos\; (\backslash \; theta\; -\; \backslash \; alpha)\}$

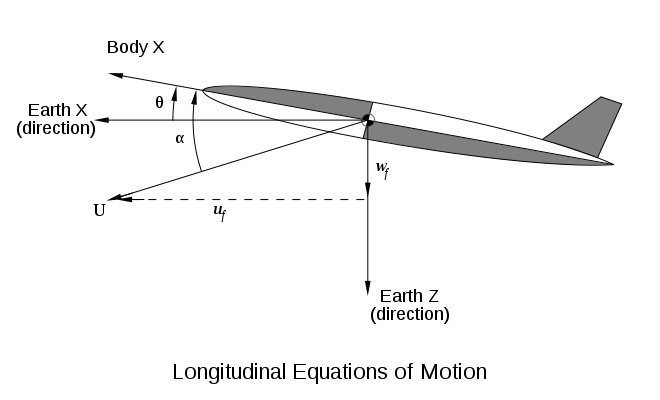
где m - масса . По характеру движения изменение скорости $md\; U\; dt\; \{\backslash \; displaystyle\; m\; \{\backslash \; frac\; \{dU\}\; \{dt\}\}\}$пренебрежимо мало за период колебания, поэтому:

$Икс\; е\; знак\; равно\; -\; м\; U\; d\; (\theta \; -\; \alpha )\; dt\; грех\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; X\_\; \{f\}\; =\; -\; mU\; \{\backslash \; frac\; \{d\; (\backslash \; theta\; -\; \backslash \; alpha)\}\; \{dt\}\}\; \backslash \; sin\; (\backslash \; тета\; -\; \backslash \; альфа)\; \}$

$Z\; е\; знак\; равно\; м\; U\; d\; (\theta \; -\; \alpha )\; dt\; соз\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; Z\_\; \{f\}\; =\; mU\; \{\backslash \; frac\; \{d\; (\backslash \; theta\; -\; \backslash \; alpha))\}\; \{dt\}\; \}\; \backslash \; cos\; (\backslash \; theta\; -\; \backslash \; alpha)\}$

Но блок распределения распределением на тело и корпус давления к вектору скорости. Но набор осей скорости (ветра) не является инерциальной системой , поэтому мы должны преобразовать силы фиксированных осей в оси ветра. Кроме того, нас интересует только сила, действующая вдоль оси z:

$Z\; =\; -\; Z\; f\; cos\; \; (\theta \; -\; \alpha )\; +\; X\; f\; sin\; \; (\theta \; -\; \alpha )\; \{\backslash \; displaystyle\; Z\; =\; -Z\_\; \{f\}\; \backslash \; соз\; (\backslash \; тета\; -\; \backslash \; альфа)\; +\; X\_\; \{е\}\; \backslash \; грех\; (\backslash \; тета\; -\; \backslash \; альфа)\}$

или:

$Z\; =\; -\; м\; U\; d\; (\theta \; -\; \alpha )\; dt\; \{\backslash \; displaystyle\; Z\; =\; -\; mU\; \{\; \backslash \; frac\; \{d\; (\backslash \; theta\; -\; \backslash \; alpha)\}\; \{dt\}\}\}$

На словах сила ветра равна центростремительному ускорению.

Уравнение момента - это производная по времени от углового момента :

$M\; =\; B\; d\; 2\; \theta \; dt\; 2\; \{\backslash \; displaystyle\; M\; =\; B\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; theta\}\; \{dt\; ^\; \{2\}\}\}\}$

где M - момент тангажа, а B - момент инерции относительно оси тангажа. Пусть: $d\; \theta \; d\; t\; =\; q\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{dt\}\}\; =\; q\}$, частота основного тона. Уравнения движения со всеми силами и моментами, относящимися к осям ветра, поэтому:

$d\; \alpha \; dt\; =\; q\; +\; Z\; m\; U\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; alpha\}\; \{dt\}\}\; =\; q\; +\; \{\backslash \; frac\; \{Z\; \}\; \{mU\}\}\}$

$dqdt\; =\; MB\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dq\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{M\}\; \{B\}\}\}$

Нас интересуют только возмущения сил и моментов, вызванные возмущениями в состояниях $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$и q, и их производные по времени. Они характеризуются производной устойчивости, определяемой из условий полета. Возможные производные устойчивости:

$Z\; \alpha \; \{\backslash \; displaystyle\; Z\; \_\; \{\backslash \; альфа\}\}$Подъем за счет падения, это отрицательно, потому что ось Z направлена ​​вниз, а положительное падение вызывает силу, направленную вверх.

$Z\; q\; \{\backslash \; displaystyle\; Z\_\; \{q\}\}$Подъем из-за скорости тангажа возникает из-за увеличения угла падения хвоста, следовательно, тоже отрицательный, но небольшой по сравнению с $Z\; \alpha \; \{\; \backslash \; displaystyle\; Z\_\; \{\backslash \; alpha\}\}$.

$M\; \alpha \; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; alpha\}\}$Момент тангажа из-за падения - термин статической устойчивости. Статическая стабильность требует, чтобы это было отрицательным.

$M\; q\; \{\backslash \; displaystyle\; M\_\; \{q\}\}$Момент тангажа из-за скорости шага - член демпфирования шага, он всегда отрицателен.

как хвост работает в поле потока крыла, изменения угла наклона крыла вызывают изменения в потоке вниз, но существует задержка для изменения потока крыла, чтобы повлиять на подъемную силу, это представлено как момент, пропорциональный к скорости изменения угла атаки:

$M\; \alpha \; \dot{}\; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; dot\; \{\backslash \; alpha\}\}\}$

Эффект отложенного смыва вниз увеличивает подъем хвоста и создает момент опускания носа, поэтому $M\; \alpha \; \dot{}\; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; dot\; \{\backslash \; alpha\}\}\}$, как ожидается, будет отрицательным.

Уравнения движения с малыми силами и моментами возмущения принимают следующий вид:

$d\; \alpha \; dt\; =\; (1\; +\; Z\; qm\; U)\; q\; +\; Z\; \alpha \; m\; U\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; alpha)\; \}\; \{dt\}\}\; =\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{Z\_\; \{q\}\}\; \{mU\}\}\; \backslash \; right)\; q\; +\; \{\backslash \; frac\; \{Z\; \_\; \{\backslash \; alpha\}\}\; \{mU\}\}\; \backslash \; alpha\}$

$dqdt\; знак\; равно\; M\; q\; В\; Q\; +\; M\; \alpha \; B\; \alpha \; +\; M\; \alpha \; \dot{}\; B\; \alpha \; \dot{}\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{dq\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{M\_\; \{q\}\}\; \{B\}\}\; q\; +\; \{\backslash \; frac\; \{M\_\; \{\backslash \; alpha\}\}\; \{B\}\}\; \backslash \; alpha\; +\; \{\backslash \; frac\; \{M\; \_\; \{\backslash \; dot\; \{\backslash \; alpha\}\}\}\; \{B\}\}\; \{\backslash \; dot\; \{\backslash \; alpha\}\}\}$

Их можно изменить, чтобы получить урожай второго порядка линейное дифференциальное уравнение в $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$:

$d\; 2\; \alpha \; dt\; 2\; -\; (Z\; \alpha \; m\; U\; +\; M\; q\; B\; +\; (1\; +\; Z\; qm\; U)\; M\; \alpha \; \dot{}\; В)\; d\; \alpha \; dt\; +\; (Z\; \alpha \; м\; UM\; q\; B\; -\; M\; \alpha \; B\; (1\; +\; Z\; Qm\; U))\; \alpha \; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; alpha\}\; \{dt\; ^\; \{\; 2\}\}\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{Z\; \_\; \{\backslash \; alpha\}\}\; \{mU\}\}\; +\; \{\backslash \; frac\; \{M\_\; \{q\}\}\; \{B\}\}\; +\; (1\; +\; \{\backslash \; frac\; \{Z\_\; \{q\}\})\; \{mU\}\}))\; \{\backslash \; frac\; \{M\; \_\; \{\backslash \; dot\; \{\backslash \; alpha\}\}\}\; \{B\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{d\; \backslash \; alpha\}\; \{dt\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{Z\; \_\; \{\backslash \; alpha\}\}\; \{mU\}\}\; \{\backslash \; frac\; \{M\_\; \{q\}\; \}\; \{B\}\}\; -\; \{\backslash \; frac\; \{M\; \_\; \{\backslash \; alpha\}\}\; \{B\}\}\; (1\; +\; \{\backslash \; frac\; \{Z\_\; \{q\}\}\; \{mU\}\})\; \backslash \; right)\; \backslash \; alpha\; =\; 0\}$

Представляет затухание простое гармоническое движение.

Мы должны ожидать, что $Z\; qm\; U\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{Z\_\; \{q\}\}\; \{mU\}\}\}$будет малым по сравнению с единицей, поэтому коэффициент $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$(термин «жесткость») будет положительным, при условии . В этом выражении преобладает $M\; \alpha \; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; alpha\}\}$, который определяет продольную статическую устойчивость самолета, она должна быть отрицательной для устойчивости. Срок демпфирования уменьшения из-за эффекта смыва вниз, и сложно спроектировать самолет с быстрой естественной реакцией и сильным демпфированием. Обычно отклик слабозатухающий, но стабильный.

Phugoid

Если ручка удерживается неподвижно, дрон не будет поддерживать прямой и горизонтальный полет (за исключением маловероятного случая, когда он идеально сбалансирован для горизонтального полета на текущей высоте и настройку тяги), но начинает нырять, выравниваться и снова набирать высоту. Он будет повторять этот цикл, пока не вмешается пилот. Это длительное колебание скорости и высоты называется режимом фугоида. Это анализируется, исходя из предположения, что SSPO выполняет свою надлежащую функцию и поддерживает угол атаки около своего номинального значения. Основное влияние оказывает два состояния: угол траектории полета $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$(гамма) и скорость. Уравнения малых возмущений:

$m\; U\; d\; \gamma \; dt\; =\; -\; Z\; \{\backslash \; displaystyle\; mU\; \{\backslash \; frac\; \{d\; \backslash \; gamma\}\; \{dt\}\}\; =\; -\; Z\}$

, что означает, что центростремительная сила равна возмущение подъемной силы.

Для скорости, разрешающей по траектории:

$mdudt\; =\; X\; -\; mg\; \gamma \; \{\backslash \; displaystyle\; m\; \{\backslash \; frac\; \{du\}\; \{dt\}\}\; =\; X-mg\; \backslash \; gamma\}$

где g - ускорение свободного падения у поверхности земли. Ускорение по траектории равно чистой силе по оси x минус компонент веса. Не следует ожидать, что существенные аэродинамические производные будут зависеть от угла траектории полета, поэтому только $X\; u\; \{\backslash \; displaystyle\; X\_\; \{u\}\}$и $Z\; u\; \{\backslash \; displaystyle\; Z\_\; \{u\}\}$необходимо учитывать. $X\; u\; \{\backslash \; displaystyle\; X\_\; \{u\}\}$- приращение сопротивления при увеличении скорости, оно отрицательное, аналогично $Z\; u\; \{\backslash \; displaystyle\; Z\_\; \{u\}\}$- приращение подъемной силы из-за приращения скорости, оно также отрицательно, потому что подъемная сила действует в противоположном направлении оси Z.

Уравнения движения принимают следующий вид:

$m\; U\; d\; \gamma \; dt\; =\; -\; Z\; uu\; \{\backslash \; displaystyle\; mU\; \{\backslash \; frac\; \{d\; \backslash \; gamma\}\; \{dt\}\}\; =\; -\; Z\_\; \{u\}\; u\}$

$mdudt\; =\; X\; uu\; -\; mg\; \gamma \; \{\backslash \; displaystyle\; m\; \{\backslash \; frac\; \{du\}\; \{dt\}\}\; =\; X\_\; \{u\}\; u-mg\; \backslash \; gamma\}$

Они могут быть выражены как уравнение второго порядка для угла траектории полета или скорости возмущение:

$d\; 2\; udt\; 2\; -\; X\; umdudt\; -\; Z\; ugm\; U\; u\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; u\}\; \{dt\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{X\_\; \{u\}\; \}\; \{m\}\}\; \{\backslash \; frac\; \{du\}\; \{dt\}\}\; -\; \{\backslash \; frac\; \{Z\_\; \{u\}\; g\}\; \{mU\}\}\; u\; =\; 0\}$

Теперь подъемная сила почти равна массе:

$Z\; Знак\; равно\; 1\; 2\; \rho \; U\; 2\; c\; LS\; w\; =\; W\; \{\backslash \; displaystyle\; Z\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; rho\; U\; ^\; \{2\}\; c\_\; \{L\}\; S\_\; \{w\}\; =\; W\}$

где $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$- плотность воздуха, $S\; w\; \{\backslash \; displaystyle\; S\_\; \{w\}\}$- площадь крыла, W - вес и $c\; L\; \{\backslash \; displaystyle\; c\_\; \{L\}\}$- коэффициент подъемной силы (предполагается постоянным, потому что угол падения постоянен), мы имеем, приблизительно:

$Z\; u\; =\; 2\; WU\; =\; 2\; мг\; U\; \{\backslash \; displaystyle\; Z\_\; \{u\}\; =\; \{\backslash \; frac\; \{2W\}\; \{U\}\}\; =\; \{\backslash \; frac\; \{2mg\}\; \{U\}\}\}$

Период t фугоид T получается из коэффициента при u:

$2\; \pi \; T\; =\; 2\; g\; 2\; U\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{2\; \backslash \; pi\}\; \{T\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2g\; ^\; \{2\}\}\; \{U\; ^\; \{2\}\}\}\}\}$

Или:

$T\; =\; 2\; \pi \; U\; 2\; g\; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{2\; \backslash \; pi\; U\}\; \{\{\backslash \; sqrt\; \{2\}\; \}\; g\}\}\}$

Поскольку подъемная сила намного больше сопротивления, фугоид в лучшем случае слегка демпфируется. Пропеллер с фиксированной скоростью может помочь. Сильное демпфирование вращения по тангажу или большая инерция вращения увеличивают связь между короткопериодными и фугоидными модами, так что они изменяют фугоид.

Боковые режимы

Для симметричной ракеты или ракеты курсовая устойчивость на рысканье такая же, как и устойчивость по тангажу; он напоминает короткопериодные колебания тангажа с плоскостью рыскания, эквивалентной производным устойчивости тангажа. По этой причине курсовая устойчивость по тангажу и рысканью вместе известна как устойчивость ракеты "флюгером".

Самолету не хватает симметрии между тангажом и рысканием, поэтому курсовая устойчивость при рысканье определяется другим набором производных устойчивости. Плоскость рыскания, эквивалентная короткопериодным колебаниям тангажа, который описывает курсовую устойчивость плоскости рыскания, называется голландским креном. В отличие от движений в плоскости тангажа, боковые режимы включают как крен, так и рыскание.

Голландский ролл

Принято выводить уравнения движения путем формальной манипуляции, что для инженера представляет собой математическую ловкость рук. Текущий подход следует за анализом плоскости шага при формулировании уравнений в терминах достаточно знакомых концепций.

Применение импульса с помощью педалей руля направления должно вызвать голландский крен, то есть колебания по крену и рысканью, с отставанием от рыскания по крену на четверть цикла, так что законцовки крыла следуют эллиптические траектории относительно самолета.

Уравнение поступательного движения в плоскости рыскания, как и в плоскости тангажа, приравнивает центростремительное ускорение к боковой силе.

$d\; \beta \; dt\; =\; Y\; m\; U\; -\; r\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{Y\}\; \{mU\}\}\; -\; r\}$

где $\beta \; \{\; \backslash \; displaystyle\; \backslash \; beta\}$(beta) - это угол бокового скольжения, Y - боковая сила и r - скорость рыскания.

Уравнения моментов немного сложнее. Условие дифферента - это когда самолет находится под углом атаки относительно воздушного потока. Ось x тела не совпадает с вектором скорости, который является опорным направлением для осей ветра. Другими словами, оси ветра не являются главными осями (масса не распределяется симметрично относительно осей рыскания и крена). Рассмотрим движение элемента массы в позиции -z, x в направлении оси y, то есть в плоскости бумаги.

Если скорость вращения равна p, скорость частицы равна:

$v\; =\; -\; pz\; +\; xr\; \{\backslash \; displaystyle\; v\; =\; -pz\; +\; xr\}$

Сила, действующая на эту частицу, состоит из двух членов. во-первых, пропорциональна скорости изменения v, во-вторых, из-за изменения направления этого компонента скорости при движении тела. Последние члены приводят к перекрестным произведениям малых количеств (pq, pr, qr), которые позже отбрасываются. В данном анализе они с самого начала отброшены для ясности. Фактически, мы предполагаем, что направление скорости частицы из-за одновременных скоростей крена и рыскания существенно не меняется на протяжении всего движения. С этим упрощающим предположением ускорение частицы становится:

$dvdt\; =\; -\; dpdtz\; +\; drdtx\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dv\}\; \{dt\}\}\; =\; -\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; z\; +\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; x\}$

Момент рыскания определяется по формуле:

$\delta \; mxdvdt\; =\; -\; dpdtxz\; \delta \; m\; +\; drdtx\; 2\; \delta \; m\; \{\backslash \; displaystyle\; \backslash \; delt\; a\; mx\; \{\backslash \; frac\; \{dv\}\; \{dt\}\; \}\; =\; -\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; xz\; \backslash \; delta\; m\; +\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; x\; ^\; \{2\}\; \backslash \; delta\; m\}$

Существует дополнительный момент рыскания из-за смещения частиц в направление y: $drdty\; 2\; \delta \; m\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; y\; ^\; \{2\}\; \backslash \; delta\; m\}$

Момент рыскания путем суммирования по всем частицам тела:

$N\; =\; -\; dpdt\; \int \; xzdm\; +\; drdt\; \int \; x\; 2\; +\; y\; 2\; dm\; =\; -\; E\; dpdt\; +\; C\; drdt\; \{\backslash \; displaystyle\; N\; =\; -\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; \backslash \; int\; xzdm\; +\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; \backslash \; int\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; dm\; =\; -E\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; +\; C\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\}$

где N - момент рыскания, E - произведение инерции, а C - момент инерции относительно оси рыскания. Аналогичное рассуждение приводит к уравнению крена:

$L\; =\; A\; dpdt\; -\; E\; drdt\; \{\backslash \; displaystyle\; L\; =\; A\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; -\; E\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\}$

где L - момент качения, A - момент инерции качения.

Производные по боковой и продольной устойчивости

Состояния: $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$(скольжение), r (скорость рыскания) и p (скорость крена)), сми N (рыскание) и L (крен) и силой Y (вбок). Есть девять производных устойчивости, относящихся к этому движению, ниже объясняется, как они работают. Однако лучшее интуитивное понимание можно получить, просто используя модель самолета и рассматривая, как силы, действующие на каждый компонент, в зависимости от изменения бокового скольжения и угловой скорости:

$Y\; \beta \; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; beta\}\}$Боковое усилие из-за бокового скольжения (при отсутствии рыскания).

Боковое скольжение боковую силу от киля и фюзеляжа. Кроме того, если крыло имеет двугранную форму, боковое скольжение при положительном угле увеличивает угол падения правого крыло и уменьшает его уменьшение на левом борту, в результате чего результирующая сила прямо противоположна стороны бокового скольжения. Размах крыльев назад оказывает такое же влияние на угол падения, но, поскольку крылья не наклонены в вертикальной плоскости, один обратный поворот не влияет на $Y\; \beta \; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; beta\}\}$. Однако в самолет с высокими летно-техническими характеристиками угла наклона можно использовать большой углами поворота, чтобы компенсировать влияние бокового скольжения крыла. Как ни странно, это не меняет знак вклада конфигурации крыла в $Y\; \beta \; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; beta\}\}$(по сравнению с двугранным случаем).

$Y\; p\; \{\backslash \; displaystyle\; Y\_\; \{p\}\}$Боковая сила из-за скорости крена.

Скорость крена вызывает на плавник, что создает соответствующую боковую силу. Кроме того, положительный крен (правое крыло вниз) увеличивает силу на правом крыле. Если крыло имеет двугранный вид, это приведет к тому, что боковая сила на мгновение будет противодействовать боковым эффектом в результате кому скольжению. Конфигурации углового крыла и / или стабилизатора могут привести к изменению знака боковой силы, если эффект плавника подавлен.

$Y\; r\; \{\backslash \; displaystyle\; Y\_\; \{r\}\}$Боковая сила из-за скорости рыскания.

Рыскание создается боковые силы из-за падения на руль направления, киль и фюзеляж.

$N\; \beta \; \{\backslash \; displaystyle\; N\; \_\; \{\backslash \; beta\}\}$Момент рыскания из-за сил бокового скольжения.

Боковое скольжение при отсутствии руля приводит к падению на фюзеляж и оперение, создавая таким образом момент рыскания, которому противодействует только направленная жесткость, которая будет иметь тенденцию указывать нос самолета назад против ветра в условиях горизонтального полета. В условиях бокового скольжения при заданном угле крена $N\; \beta \; \{\backslash \; displaystyle\; N\; \_\; \{\backslash \; beta\}\}$будет иметь тенденцию указывать носом в направлении бокового скольжения даже без нажатия руля направления, вызывая полет по спирали вниз.

$N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$Момент рыскания из-за скорости крена.

Скорость крена создает подъемную силу плавника, вызывающую рыскание, а также по-разному изменяет подъемную силу на крыльях, таким образом влияя на вклад индуцированного сопротивления каждого крыла, вызывающий (небольшой) вклад момента рыскания. Положительный крен обычно приводит к положительным значениям $N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$, если только оперение не является угловым или ребро не находится ниже оси крена. Компоненты поперечной силы, возникающие в результате двугранной или угловой разницы подъемной силы крыла, мало влияют на $N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$, поскольку ось крыла обычно близко выровнена с центром тяжести.

$N\; r\; \{\backslash \; displaystyle\; N\_\; \{r\}\}$Момент рыскания из-за скорости рыскания.

Ввод скорости рыскания при любом угле крена генерирует векторы силы руля, киля и фюзеляжа, которые доминируют в результирующем моменте рыскания.. Рыскание также увеличивает скорость внешнего крыла, одновременно замедляя внутреннее крыло, с соответствующими изменениями сопротивления, вызывающими (небольшой) противоположный момент рыскания. $N\; r\; \{\backslash \; displaystyle\; N\_\; \{r\}\}$противостоит присущей направленной жесткости, которая имеет тенденцию указывать нос самолета назад против ветра и всегда соответствует знаку входной скорости рыскания.

$L\; \beta \; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\}$Момент качения из-за бокового скольжения.

Положительный угол бокового скольжения создает угол оперения, который может вызывать положительный или отрицательный момент крена в зависимости от его конфигурации. При любом ненулевом угле бокового скольжения двугранные крылья вызывают крутящий момент, который стремится вернуть самолет в горизонтальное положение, как и крылья с обратной стреловидностью. В случае крыльев с большой стреловидностью результирующий момент качения может быть чрезмерным для всех требований устойчивости, и можно использовать угол наклона для компенсации эффекта момента качения, вызванного стреловидностью крыла.

$L\; r\; \{\backslash \; displaystyle\; L\_\; \{r\}\}$Момент качения из-за скорости рыскания.

Рыскание увеличивает скорость внешнего крыла, одновременно снижая скорость внутреннего крыла, вызывая вращающий момент внутренняя сторона. Вклад ребра обычно поддерживает этот эффект качения внутрь, если только он не компенсируется угловым стабилизатором над осью крена (или двугранным под осью крена).

$L\; p\; \{\backslash \; displaystyle\; L\_\; \{p\}\}$Момент качения из-за скорости крена.

Крен создает противодействующие силы вращения как на правом, так и на левом крыле, а также создает такие силы на оперении. Эти противоположные эффекты момента качения должны преодолеваться входом элеронов, чтобы поддерживать скорость крена. Если крен остановлен при ненулевом угле крена, то $L\; \beta \; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\}$момент качения вверх, вызванный последующим боковым скольжением, должен вернуть самолет в горизонтальное положение, если он не превышен. в свою очередь, направленным вниз $L\; r\; \{\backslash \; displaystyle\; L\_\; \{r\}\}$моментом качения, возникающим из-за скорости рыскания, вызванной боковым скольжением. Продольную устойчивость можно обеспечить или улучшить за счет минимизации последнего эффекта.

Уравнения движения

Поскольку Голландский крен является режимом обработки, аналогичным короткопериодным колебаниям шага, любое влияние, которое оно могло бы оказать на траекторию, можно игнорировать. Скорость тела r складывается из скорости изменения угла бокового скольжения и скорости поворота. Принимая последнее за ноль, предполагая, что это не влияет на траекторию, для ограниченной цели изучения голландского разворота:

$d\; \beta \; dt\; =\; -\; r\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; =\; -\; r\; \}$

Уравнения рысканья и крена с производными устойчивости становятся:

$C\; drdt\; -\; E\; dpdt\; =\; N\; \beta \; \beta \; -\; N\; rd\; \beta \; dt\; +\; N\; pp\; \{\backslash \; displaystyle\; C\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; -E\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; =\; N\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; -N\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; +\; N\_\; \{p\}\; p\}$(рыскание)

$A\; dpdt\; -\; E\; drdt\; =\; L\; \beta \; \beta \; -\; L\; rd\; \beta \; dt\; +\; L\; pp\; \{\backslash \; displaystyle\; A\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; -\; E\; \{\backslash \; frac\; \{dr\}\; \{dt\}\}\; =\; L\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; -L\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; +\; L\_\; \{p\}\; p\}$(roll)

Инерционный момент из-за переката ускорение считается небольшим по сравнению с аэродинамическими условиями, поэтому уравнения принимают следующий вид:

$-\; C\; d\; 2\; \beta \; dt\; 2\; =\; N\; \beta \; \beta \; -\; N\; rd\; \beta \; dt\; +\; N\; pp\; \{\backslash \; displaystyle\; -C\; \{\backslash \; frac\; \{d\; ^\; \{2\; \}\; \backslash \; beta\}\; \{dt\; ^\; \{2\}\}\}\; =\; N\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; -N\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; +\; N\_\; \{p\}\; p\}$

$E\; d\; 2\; \beta \; dt\; 2\; знак\; равно\; L\; \beta \; \beta \; -\; L\; rd\; \beta \; dt\; +\; L\; pp\; \{\backslash \; displaystyle\; E\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; beta\}\; \{dt\; ^\; \{2\}\}\}\; =\; L\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; -L\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; +\; L\_\; \{p\}\; p\}$

Это становится уравнением второго порядка, определяющим скорость крена или скольжение:

$(N\; p\; CEA\; -\; L\; p\; A)\; d\; 2\; \beta \; dt\; 2\; +\; (L\; п\; AN\; р\; С\; -\; N\; п\; CL\; р\; A)\; d\; \beta \; dt\; -\; (L\; п\; AN\; \beta \; C\; -\; L\; \beta \; AN\; п\; C)\; \beta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \{\backslash \; frac\; \{E\}\; \{A\}\}\; -\; \{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; beta\}\; \{dt\; ^\; \{2\}\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\}\}\; \{\backslash \; frac\; \{N\_\; \{r\}\}\; \{C\}\}\; -\; \{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \{\; \backslash \; frac\; \{L\_\; \{r\}\}\; \{A\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{d\; \backslash \; beta\}\; \{dt\}\}\; -\; \backslash \; left\; (\{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\}\}\; \{\backslash \; frac\; \{N\_\; \{\; \backslash \; beta\}\}\; \{C\}\}\; -\; \{\backslash \; frac\; \{L\; \_\; \{\backslash \; beta\}\}\; \{A\}\}\; \{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \backslash \; right)\; \backslash \; beta\; =\; 0\}$

Уравнение для скорость крена идентична. Но угол крена, $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$(phi), определяется как:

$d\; \varphi \; dt\; =\; p\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{dt\}\; \}\; =\; p\}$

Если p - затухающее простое гармоническое движение, то же самое и $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$, но крен должен быть в квадратуре с скорость крена, а значит, и скольжение. Движение состоит из колебаний по крену и рысканью, при этом крен отстает на 90 градусов от рыскания. Концы крыла очерчивают эллиптические траектории.

Устойчивость требует, чтобы термины «жесткость » и «демпфирование» были положительными. Это:

$L\; p\; AN\; r\; C\; -\; N\; p\; CL\; r\; AN\; p\; CEA\; -\; L\; p\; A\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\}\}\; \{\backslash \; frac\; \{N\_\; \{r)\; \}\}\; \{C\}\}\; -\; \{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \{\backslash \; frac\; \{L\_\; \{r\}\}\; \{A\}\}\}\; \{\{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \{\backslash \; frac\; \{E\}\; \{A\}\}\; -\; \{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\}\}\}\}\}$(демпфирование)

$L\; \beta \; AN\; p\; C\; -\; L\; p\; AN\; \beta \; CN\; p\; CEA\; -\; L\; п\; A\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; frac\; \{L\; \_\; \{\backslash \; beta\}\}\; \{A\}\}\; \{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; -\; \{\backslash \; frac\; \{L\_\; \{p\}\}\; \{A\; \}\}\; \{\backslash \; frac\; \{N\; \_\; \{\backslash \; beta\}\}\; \{C\}\}\}\; \{\{\backslash \; frac\; \{N\_\; \{p\}\}\; \{C\}\}\; \{\backslash \; frac\; \{E\}\; \{A\}\}\; -\; \{\backslash \; frac\; \{L\_\; \{p\}\; \}\; \{A\}\}\}\}\}$(жесткость)

В знаменателе преобладает $L\; p\; \{\backslash \; displaystyle\; L\_\; \{p\}\}$, производная демпфирования крена, которое всегда отрицательно, поэтому знаменатели этих двух выражений будут положительными.

Учитывая термин "жесткость": $-\; L\; p\; N\; \beta \; \{\backslash \; displaystyle\; -L\_\; \{p\}\; N\; \_\; \{\backslash \; beta\}\}$будет положительным, потому что $L\; p\; \{\backslash \; displaystyle\; L\_\; \{p\}\}$всегда отрицательно, а $N\; \beta \; \{\backslash \; displaystyle\; N\; \_\; \{\backslash \; beta\}\}$изначально положительно. $L\; \beta \; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\}$обычно отрицательно, а $N\; p\; \{\backslash \; displaystyle\; N\_\; \{p\}\}$- положительно. Чрезмерный двугранный угол может дестабилизировать голландский крен, поэтому конфигурации с сильно стреловидными крыльями требуют наличия углового угла, чтобы компенсировать вклад стреловидности крыла в $L\; \beta \; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\}$.

В параметре демпфирования преобладает произведение демпфирование крена и производные демпфирования рыскания отрицательны, поэтому их произведение положительно. Поэтому голландский рулон должен быть демпфированным.

Движение сопровождается небольшим боковым перемещением центра тяжести, и более «точный» анализ представит термины в $Y\; \beta \; \{\backslash \; displaystyle\; Y\; \_\; \{\backslash \; beta\}\}$и т.п. Принимая во внимание точность, с которой могут быть вычислены производные устойчивости, это излишняя педантичность, которая скрывает взаимосвязь между геометрией самолета и управляемостью, которая является основной целью данной статьи.

Проседание рулона

Дергание рукояти в сторону и возвращение ее в центр вызывает чистое изменение ориентации рулона.

Креновое движение характеризуется отсутствием естественной устойчивости, отсутствуют производные устойчивости, которые создают моменты в ответ на инерционный угол крена. Помехи крена вызывают скорость крена, которая отменяется только пилотом или вмешательством автопилота. Это происходит при незначительных изменениях скорости скольжения или рыскания, поэтому уравнение движения сводится к:

$A\; d\; p\; d\; t\; =\; L\; p\; p.\; \{\backslash \; displaystyle\; A\; \{\backslash \; frac\; \{dp\}\; \{dt\}\}\; =\; L\_\; \{p\}\; p.\}$

$L\; p\; \{\backslash \; displaystyle\; L\_\; \{p\}\}$отрицательно, поэтому скорость поворота будет уменьшаться с течением времени. Скорость крена снижается до нуля, но нет прямого контроля над углом крена.

Спиральный режим

Если просто удерживать ручку неподвижно, при старте с крыльями, близкими к горизонтальному, самолет обычно будет иметь тенденцию постепенно отклоняться в сторону от прямой траектории полета. Это (слегка нестабильная) спиральная мода .

Спиральная мода траектория

При изучении траектории интерес представляет скорее направление вектора скорости, чем направление тела. Направление вектора скорости при проецировании на горизонталь будет называться треком, обозначенным $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$(mu ). Ориентация тела называется заголовком и обозначается $\psi \; \{\backslash \; displaystyle\; \backslash \; psi\}$(psi). Уравнение движения силы включает компонент веса:

$d\; \mu \; dt\; =\; Y\; m\; U\; +\; g\; U\; \varphi \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\}\}\; =\; \{\backslash \; frac\; \{Y\}\; \{mU\}\; \}\; +\; \{\backslash \; frac\; \{g\}\; \{U\}\}\; \backslash \; phi\}$

где g - ускорение свободного падения, а U - скорость.

Включая производные устойчивости:

$d\; \mu \; dt\; =\; Y\; \beta \; m\; U\; \beta \; +\; Y\; rm\; U\; r\; +\; Y\; pm\; U\; p\; +\; g\; U\; \varphi \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\; \}\}\; =\; \{\backslash \; frac\; \{Y\; \_\; \{\backslash \; beta\}\}\; \{mU\}\}\; \backslash \; beta\; +\; \{\backslash \; frac\; \{Y\_\; \{r\}\}\; \{mU\}\}\; r\; +\; \{\backslash \; frac\; \{Y\_\; \{p\}\}\; \{mU\}\}\; p\; +\; \{\backslash \; frac\; \{g\}\; \{U\}\}\; \backslash \; phi\}$

Ожидается, что скорость крена и рыскания будет небольшой, поэтому вклад $Y\; r\; \{\backslash \; displaystyle\; Y\_\; \{r\}\}$и $Y\; p\; \{\backslash \; displaystyle\; Y\_\; \{p\}\}$будет проигнорировано.

Скорость скольжения и крена изменяется постепенно, поэтому их временные производные игнорируются. Уравнения рыскания и крена сводятся к:

$N\; \beta \; \beta \; +\; N\; rd\; \mu \; dt\; +\; N\; pp\; =\; 0\; \{\backslash \; displaystyle\; N\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; +\; N\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\}\; \}\; +\; N\_\; \{p\}\; p\; =\; 0\}$(рыскание)

$L\; \beta \; \beta \; +\; L\; rd\; \mu \; dt\; +\; L\; pp\; =\; 0\; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\; \backslash \; beta\; +\; L\_\; \{r\}\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\}\}\; +\; L\_\; \{p\}\; p\; =\; 0\}$(roll)

Решение для $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$и п:

$\beta \; =\; (L\; р\; N\; п\; -\; L\; п\; N\; р)\; (L\; п\; N\; \beta \; -\; N\; п\; L\; \beta )\; d\; \mu \; dt\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; \{\backslash \; frac\; \{(L\_\; \{r\}\; N\_\; \{p\}\; -L\_\; \{p\}\; N\_\; \{r\})\}\; \{(L\_\; \{p\}\; N\; \_\; \{\backslash \; beta\}\; -N\_\; \{p\}\; L\; \_\; \{\backslash \; beta\})\}\}\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\}\}\; \}$

$п\; =\; (L\; \beta \; N\; р\; -\; L\; р\; N\; \beta )\; (L\; п\; N\; \beta \; -\; N\; п\; L\; \beta )\; d\; \mu \; dt\; \{\backslash \; displaystyle\; p\; =\; \{\backslash \; frac\; \{(L\; \_\; \{\backslash \; beta\}\; N\_\; \{r\})\; -L\_\; \{r\}\; N\; \_\; \{\backslash \; beta\})\}\; \{(L\_\; \{p\}\; N\; \_\; \{\backslash \; beta\}\; -N\_\; \{p\}\; L\; \_\; \{\backslash \; beta\})\}\}\; \{\backslash \; frac\; \{d\; \backslash \; mu\}\; \{dt\}\}\}$

Подстановка бокового скольжения и скорости крена в уравнение силы приводит к уравнению первого порядка по углу крена:

$d\; \varphi \; dt\; =\; mg\; (L\; \beta \; N\; r\; -\; N\; \beta \; L\; r)\; m\; U\; (L\; p\; N\; \beta \; -\; N\; п\; L\; \beta )\; -\; Y\; \beta \; (L\; р\; N\; п\; -\; L\; п\; N\; р)\; \varphi \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{dt\}\}\; =\; mg\; \{\backslash \; frac\; \{(L\; \_\; \{\backslash \; beta\}\; N\_\; \{r\})\; -N\; \_\; \{\backslash \; beta\}\; L\_\; \{r\})\}\; \{mU\; (L\_\; \{p\}\; N\; \_\; \{\backslash \; beta\; \}\; -N\_\; \{p\}\; L\; \_\; \{\backslash \; beta\})\; -\; Y\; \_\; \{\backslash \; beta\}\; (L\_\; \{r\}\; N\_\; \{p\}\; -L\_\; \{p\}\; N\_\; \{r\})\}\}\; \backslash \; phi\}$

Это экспоненциальный рост или спад, в зависимости от того, является ли коэффициент $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\}$положительным или отрицательным. Знаменатель обычно отрицательный, что требует $L\; \beta \; N\; r>N\; \beta \; L\; r\; \{\backslash \; displaystyle\; L\; \_\; \{\backslash \; beta\}\; N\_\; \{r\}>N\; \_\; \{\backslash \; beta\}\; L\_\; \{r\}\}$( оба продукта положительны). Это прямо противоречит голландским требованиям к устойчивости к качению, и трудно спроектировать самолет, для которого и голландский режим крена, и спиральный режим по своей природе стабильны.

Поскольку спиральный режим имеет длительную постоянную времени, пилот может вмешаться, чтобы эффективно стабилизировать его, но самолету с нестабильным голландским креном будет трудно летать. Обычно самолет проектируется с устойчивым голландским режимом крена, но слегка режим нестабильной спирали.

Акронимы и сокращения в авионике Аэронавтика Устойчивый полет Система управления полетом самолета Механика полета самолета Заголовок самолета Авиационный банк Cr Посадка osswind Динамическое позиционирование Поверхности управления полетом

Динамика вертолета JSBSim (программная модель динамики полета с открытым исходным кодом) Продольная статическая устойчивость Динамика твердого тела Вращение матрица Движение судов Производные по устойчивости Статический запас Исследовательский самолет с переменным откликом Эффект флюгера Планер Райта 1902 года

Примечания

Библиография

• Н.К. Синха и Н. Ананткришнан (2013), Элементарная динамика полета с введением в методы бифуркации и продолжения, CRC Press, Taylor Francis.
• Бабистер, AW (1980). Динамическая устойчивость и реакция самолета (1-е изд.). Оксфорд: Pergamon Press. ISBN 978-0080247687.
• Стенгель, Роберт Ф. (2004). Динамика полета. Принстон, Нью-Джерси: Princeton University Press. ISBN 0-691-11407-2.

• Фреймворк моделирования с открытым исходным кодом на C ++
• Библиотека программного обеспечения с открытым исходным кодом, независимая от платформы, динамического управления и управления движением на C ++