Теорема об остатке

Математический анализ → Комплексный анализ
Комплексный анализ
Сложные числа
Настоящий номер Мнимое число Сложная плоскость Комплексное сопряжение Комплексное число единицы
Сложные функции
Комплексная функция Аналитическая функция Голоморфная функция Уравнения Коши – Римана Формальный степенной ряд
Основная теория
Нули и полюсы Интегральная теорема Коши Местный примитив Интегральная формула Коши Номер обмотки Серия Laurent Изолированная особенность Теорема об остатке Конформная карта Лемма Шварца Гармоническая функция Уравнение Лапласа
Геометрическая теория функций
Люди
Огюстен-Луи Коши Леонард Эйлер Карл Фридрих Гаусс Жак Адамар Киёси Ока Бернхард Риманн Карл Вейерштрасс
Математический портал
v т е

В комплексном анализе, то остаток теорема, которую иногда называют остаток теоремы Коши, является мощным инструментом для оценки линейных интегралов от аналитических функций над замкнутыми кривыми; его часто можно использовать для вычисления действительных интегралов и бесконечных рядов. Она обобщает интегральную теорему Коши и интегральная формула Коши. С геометрической точки зрения это можно рассматривать как частный случай обобщенной теоремы Стокса.

• 1 Заявление
• 2 Примеры
  • 2.1 Интеграл по действительной оси
  • 2.2 Бесконечная сумма
• 3 См. Также
• 4 Примечания
• 5 ссылки
• 6 Внешние ссылки

Заявление выглядит следующим образом:

Иллюстрация постановки.

Пусть U будет односвязной открытое подмножество в комплексной плоскости, содержащей конечный список точек на 1,..., а п, U 0 = U \ { 1,..., п } и функция F определена и голоморфна на U 0. Пусть γ замкнутая спрямляемая кривой в U 0, и обозначит обмотку числа из гаммы вокруг в к от I ( γ, к). Криволинейный интеграл F вокруг Г равен 2 л я кратная сумма остатков из F в точках, каждый считается столько раз, сколько γ ветры вокруг точки:

${\ displaystyle \ oint _ {\ gamma} f (z) \, dz = 2 \ pi i \ sum _ {k = 1} ^ {n} \ operatorname {I} (\ gamma, a_ {k}) \ operatorname {Res} (f, a_ {k}).}$

Если γ является положительно ориентированный простой замкнутой кривой, I ( γ, к) = 1, если к находится во внутренней части Г, и 0, если нет, следовательно,

${\ displaystyle \ oint _ {\ gamma} f (z) \, dz = 2 \ pi i \ sum \ operatorname {Res} (f, a_ {k})}$

с суммой по тем a k внутри γ.

Связь теоремы о вычетах с теоремой Стокса дается теоремой о жордановой кривой. Общая плоская кривая γ сначала должна быть приведена к набору простых замкнутых кривых { γ i }, сумма которых эквивалентна γ для целей интегрирования; это сводит задачу к нахождению интеграла от ф иг вдоль кривой Жордана amp; gamma ; I с объемным V. Требование голоморфности f на U 0 = U \ { a k } эквивалентно утверждению, что внешняя производная d ( f dz) = 0 на U 0. Таким образом, если две плоские области V и W из U охватывают одно и то же подмножество { a j } из { a k }, области V \ W и W \ V целиком лежат в U 0, и, следовательно,

${\ displaystyle \ int _ {V \ smallsetminus W} d (f \, dz) - \ int _ {W \ smallsetminus V} d (f \, dz)}$

хорошо определена и равна нулю. Следовательно, контурный интеграл f dz вдоль γ j = ∂V равен сумме набора интегралов вдоль путей λ j, каждый из которых охватывает произвольно малую область вокруг единственного a j - вычетов f (с точностью до обычного множитель 2 π i) в { a j }. Суммируя по { γ j }, получаем окончательное выражение контурного интеграла через числа витков {I ( γ, a k)}.

Чтобы вычислить действительные интегралы, теорема о вычетах используется следующим образом: подынтегральное выражение расширяется на комплексную плоскость и вычисляются его вычеты (что обычно легко), а часть вещественной оси продолжается до замкнутой кривой. прикрепив полукруг в верхней или нижней полуплоскости, образуя полукруг. Затем интеграл по этой кривой можно вычислить с помощью теоремы о вычетах. Часто полукруглая часть интеграла будет стремиться к нулю по мере увеличения радиуса полукруга, оставляя только действительную часть интеграла, ту, которая нас интересовала изначально.

Интеграл по действительной оси

Интегральный

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itx}} {x ^ {2} +1}} \, dx}$

Контур С.

возникает в теории вероятностей при вычислении характеристической функции от распределения Коши. Он сопротивляется методам элементарного исчисления, но может быть оценен, выразив его как предел контурных интегралов.

Предположим, что t gt; 0, и определим контур C, который идет вдоль вещественной прямой от - a до a, а затем против часовой стрелки по полукругу с центром в 0 от a до - a. Возьмите a больше 1, чтобы мнимая единица i была заключена в кривую. Теперь рассмотрим контурный интеграл

${\ displaystyle \ int _ {C} {f (z)} \, dz = \ int _ {C} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz.}$

Поскольку e ^itz - целая функция (не имеющая особенностей ни в одной точке комплексной плоскости), эта функция имеет особенности только там, где знаменатель z ² + 1 равен нулю. Поскольку z ² + 1 = ( z + i) ( z - i), это происходит только тогда, когда z = i или z = - i. Только одна из этих точек находится в области, ограниченной этим контуром. Поскольку F ( г) является

${\ displaystyle {\ begin {align} {\ frac {e ^ {itz}} {z ^ {2} +1}} amp; = {\ frac {e ^ {itz}} {2i}} \ left ({\ frac {1} {zi}} - {\ frac {1} {z + i}} \ right) \\ amp; = {\ frac {e ^ {itz}} {2i (zi)}} - {\ frac { e ^ {itz}} {2i (z + i)}}, \ end {выровнено}}}$

остаток из F ( г) при г = я являюсь

${\ displaystyle \ operatorname {Res} _ {z = i} f (z) = {\ frac {e ^ {- t}} {2i}}.}$

Тогда согласно теореме о вычетах имеем

${\ Displaystyle \ int _ {C} е (z) \, dz = 2 \ pi i \ cdot \ operatorname {Res} \ limits _ {z = i} f (z) = 2 \ pi i {\ frac {e ^ {- t}} {2i}} = \ pi e ^ {- t}.}$

Контур C можно разделить на прямую часть и криволинейную дугу, так что

${\ Displaystyle \ int _ {\ mathrm {прямо}} f (z) \, dz + \ int _ {\ mathrm {arc}} f (z) \, dz = \ pi e ^ {- t} \,}$

и поэтому

${\ displaystyle \ int _ {- a} ^ {a} f (z) \, dz = \ pi e ^ {- t} - \ int _ {\ mathrm {arc}} f (z) \, dz.}$

Используя некоторые оценки, имеем

${\ displaystyle \ left | \ int _ {\ mathrm {arc}} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz \ right | \ leq \ pi a \ cdot \ sup _ {\ text {arc}} \ left | {\ frac {e ^ {itz}} {z ^ {2} +1}} \ right | \ leq \ pi a \ cdot \ sup _ {\ text {arc }} {\ frac {1} {| z ^ {2} +1 |}} \ leq {\ frac {\ pi a} {a ^ {2} -1}},}$

а также

${\ displaystyle \ lim _ {a \ to \ infty} {\ frac {\ pi a} {a ^ {2} -1}} = 0.}$

Оценка на числитель следует, так как т gt; 0, так и для комплексных чисел г вдоль дуги (которая лежит в верхней полуплоскости), аргумент φ из г лежит между 0 и П. Так,

${\ displaystyle \ left | e ^ {itz} \ right | = \ left | e ^ {it | z | (\ cos \ varphi + i \ sin \ varphi)} \ right | = \ left | e ^ {- t | z | \ sin \ varphi + it | z | \ cos \ varphi} \ right | = e ^ {- t | z | \ sin \ varphi} \ leq 1.}$

Следовательно,

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz = \ pi e ^ {- t}.}$

Если t lt;0, то аналогичный аргумент с дугой C ′, которая вьется вокруг - i, а не i, показывает, что

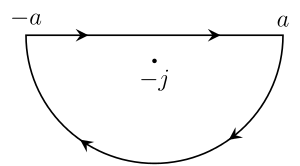
Контур C ′.

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz = \ pi e ^ {t},}$

и наконец у нас есть

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} {\ frac {e ^ {itz}} {z ^ {2} +1}} \, dz = \ pi e ^ {- \ left | t \ right |}.}$

(Если t = 0, то интеграл немедленно поддается элементарным методам исчисления и его значение равно π.)

Бесконечная сумма

Тот факт, что π cot ( πz) имеет простые полюсы с вычетом 1 при каждом целом числе, можно использовать для вычисления суммы

${\ displaystyle \ displaystyle \ sum _ {n = - \ infty} ^ {\ infty} f (n).}$

Рассмотрим, например, f ( z) = z ⁻². Пусть Γ N - прямоугольник, являющийся границей [- N - 1/2, N +1/2] ² с положительной ориентацией, с целым числом N. По формуле вычета

${\ displaystyle {\ frac {1} {2 \ pi i}} \ int _ {\ Gamma _ {N}} f (z) \ pi \ cot (\ pi z) \, dz = \ operatorname {Res} \ ограничивает _ {z = 0} + \ sum _ {n = -N \ atop n \ neq 0} ^ {N} n ^ {- 2}.}$

Левая часть обращается в нуль при N → ∞, поскольку подынтегральное выражение имеет порядок. С другой стороны, ${\ Displaystyle О (п ^ {- 2})}$

${\ displaystyle {\ frac {z} {2}} \ cot \ left ({\ frac {z} {2}} \ right) = 1-B_ {2} {\ frac {z ^ {2}} {2 !}} + \ cdots \ qquad}$где число Бернулли ${\ displaystyle B_ {2} = {\ frac {1} {6}}.}$

(По факту, z/2 детская кроватка (z/2знак равно iz/1 - е ^{- из} - iz/2.) Таким образом, вычет Res z = 0 равен -π ²/3. Мы заключаем:

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {2}}} = {\ frac {\ pi ^ {2}} {6}}}$

что является доказательством проблемы Базеля.

Тот же прием можно использовать для определения суммы ряда Эйзенштейна :

${\ displaystyle \ pi \ cot (\ pi z) = \ lim _ {N \ to \ infty} \ sum _ {n = -N} ^ {N} (zn) ^ {- 1}.}$

Возьмем f ( z) = ( w - z) ^−1, где w нецелое число, и мы покажем вышесказанное для w. Сложность в этом случае состоит в том, чтобы показать обращение в нуль контурного интеграла на бесконечности. У нас есть:

${\ displaystyle \ int _ {\ Gamma _ {N}} {\ frac {\ pi \ cot (\ pi z)} {z}} \, dz = 0}$

так как подынтегральная функция является четной функцией, и поэтому вклады контура в левой полуплоскости и контура в правой компенсируют друг друга. Таким образом,

${\ displaystyle \ int _ {\ Gamma _ {N}} f (z) \ pi \ cot (\ pi z) \, dz = \ int _ {\ Gamma _ {N}} \ left ({\ frac {1 } {wz}} + {\ frac {1} {z}} \ right) \ pi \ cot (\ pi z) \, dz}$

стремится к нулю при N → ∞.

• Интегральная формула Коши
• Основная теорема Глассера
• Лемма Джордана
• Способы контурной интеграции
• Теорема Мореры
• Теорема Нахбина
• Остаток на бесконечности
• Логарифмическая форма

• Альфорс, Ларс (1979). Комплексный анализ. Макгроу Хилл. ISBN   0-07-085008-9.
• Линделёф, Эрнст Л. (1905). Le Calcul des résidus et ses applications à la théorie des fonctions (на французском языке). Издания Жака Габа (опубликовано в 1989 г.). ISBN   2-87647-060-8.
• Митринович, Драгослав; Кечкич, Йован (1984). Метод вычетов Коши: теория и приложения. Издательство Д. Рейдел. ISBN   90-277-1623-4.
• Whittaker, ET ; Уотсон, GN (1920). Курс современного анализа (3-е изд.). Издательство Кембриджского университета.

• "Интегральная теорема Коши", Математическая энциклопедия, EMS Press, 2001 [1994]
• Теорема об остатках в MathWorld