Войти
A координатной сетки на Земле в виде сфере или эллипсоид. Линии от полюса к полюсу - это постоянная линия долготы или меридианов . Окружности, параллельные экватору, являются линией постоянной широты или параллельными . Сетка показывает широту и долготу точек на поверхности. В этом примере меридианы расположены с интервалом 6 °, а параллели с интервалом 4 °. В география, широта - это географическая координата, которая указывает север - юг положение точки на поверхности Земли. Широта - это угол (определенный ниже), который колеблется от 0 ° на экваторе до 90 ° (север или юг) на полюсах. Линии постоянной широты или параллели проходят с востока на запад в виде окружностей параллельных экватору. Широта используется вместе с долготой для определения точного местоположения объектов на поверхности Земли. Сам по себе термин «широта» следует понимать как геодезическую широту, как определено ниже. Вкратце, геодезическая широта в точке - это угол, образованный вектором, перпендикулярным (или нормалью ) к эллипсоидальной поверхности от этой точки и к экваториальной плоскости. Также шесть дополнительных широт, которые используются в специальных приложениях.
Два уровня абстракции используются для определения широты и долготы. На первом этапе физическая поверхность моделируется геоидом , поверхность, которая соответствует среднему уровню моря над океанами и его продолжению под сушей. Второй шаг состоит в аппроксимации геоида с помощью математически простой опорной поверхности. Самый простой выбор для опорной поверхности является шар, а геоид более точно моделируется эллипсоид. Определения широты и долготы на таких опорных поверхностях подробно в следующих разделах. Линии постоянной широты и долготы в совокупности составляют координатная сетка на опорной поверхности. Широта точки на фактической поверхности является то, что соответствующей точки на опорной поверхности, соответствие быть вдоль нормальный к опорной поверхности, которая проходит через точку на физической поверхности. Широта и долгота вместе с некоторой спецификацией height составляют географическую систему координат, как определено в соответствии со стандартом ISO 19111.
Временная система много разных составляет, точная широта объекта на поверхности не является уникальной: это обозначено в стандарте ISO, который гласит, что «без полной спецификации системы координат» (т.е. широта и долгота) в лучшем случае неоднозначно, в худшем - бессмысленно ". Важная в точных приложениях, таких как Глобальная система позиционирования (GPS), но при обычном использовании, где не требуется высокая точность, опорный эллипсоид обычно не указывается.
В английских текстах угол широты, определяемый ниже, обычно обозначается строчной греческой буквой phi (φ или ϕ). Он измеряется в градусах, минутах и секундах или десяти градусах к северу или югу от экватора. ции указываются в градусах и десятичных минутах. Например, маяк Иглс находится на 50 ° 39,734'N 001 ° 35,500'W.
Для точного измерения широты требуется понимание гравитационного поля Земли, либо для установки теодолитов или для определения спутниковых орбитов GPS. Изучение фигуры Земли вместе с ее гравитационным полем - это наука геодезия.
Эта статья относится к системам координат Земли: она может быть расширена, чтобы покрыть Луну, планету. и другие небесные объекты путем простого изменения номенклатуры.
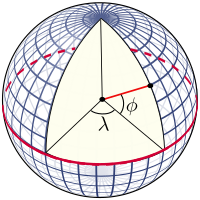Перспективный вид Земли, показывающий, как широта (
) и долгота (
) Решенное на сферической модели. Шаг сетки составляет 10 градусов. Масштабная сетка образована линиями широты постоянной долготы, которые построены относительно оси вращения Земли. Первичные контрольные точки - это полюса, где ось вращения Земли пересекает контрольную поверхность. Плоскости, пересекают ось, пересекают поверхность по меридианам ; а угол между любой плоскостью меридиана и плоскостью, проходящей через Гринвич (Главный меридиан ), определяет долготу: меридианы - это линии постоянной долготы. Плоскость, проходящая через центр Земли и перпендикулярная ось вращения, пересекает поверхность по большой окружности, называемой экватором. Плоскости, параллельные экваториальной плоскости, пересекают поверхность кругами постоянной широты; это параллели. Экватор имеет широту 0 °, Северный полюс имеет широту 90 ° северной широты (записывается 90 ° с.ш. или + 90 °), а Южный полюс имеет широту 90 ° южной широты (пишется 90 ° южной широты или -90 °). Широта произвольной точки - это угол между экваториальной плоскостью и нормалью к поверхности в этой точке: нормаль к поверхности сферы проходит по радиус-вектору.
Широту, как определено таким образом, сфера, называется часто сферической широтой, чтобы избежать двусмысленности с геодезической широтой и вспомогательными широтами, определенными в разделах этой статьи.
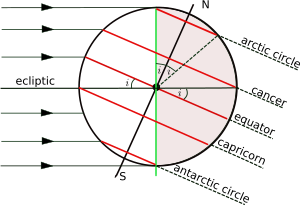Ориентация Земли в период декабрьского солнцестояния. Помимо экватора, важны еще четыре параллели:
| Полярный круг | 66 ° 34 ′ (66,57 °) с.ш. |
| тропик Рака | 23 ° 26 '(23,43 °) с.ш. |
| тропик Козерога | 23 ° 26 '(23,43 °) ю.ш. |
| Южный полярный круг | 66 ° 34 ′ (66,57 °) ю.ш. |
скость орбиты Земли вокруг Солнца называется эклиптикой, плоскость, перпендикулярная ось вращения Земли, является плоскостью экватора. Угол между эклиптикой и экваториальной плоскостью называется по-разному осевым наклоном, наклоном или наклоном эклиптики и условно обозначается i. Широта тропических кругов равна i, а широта полярных кругов является дополнением (90 ° - i). Ось медленно меняется со временем, приведенные здесь значения, являются значениями для текущей эпохи. Изменение во времени более полно обсуждается в статье о наклоне оси.
. На рисунке геометрия сечения плоскости, перпендикулярной эклиптике и проходящей через центры Земли и Земли. Солнце в декабрьское солнцестояние, когда Солнце находится над головой в некоторой точке Тропика Козерога. На южных полярных широтах ниже Южного полярного круга наблюдается дневной свет, а на северных полярных широтах за полярным кругом - ночь. Ситуация меняется на противоположную во время июньского солнцеста, когда Солнце находится над головой в тропике Рака. Только на широтах между двумя тропиками Солнце может находиться прямо над головой (в зените ).
На картографических проекциях нет универсальных правил относительно того, как должны быть меридианы и параллели. В приведенных примерах ниже показаны названные параллели (в виде красных линий) на обычно используемой проекции Меркатора и поперечной проекции Меркатора. На первом параллели горизонтальны, а меридианы вертикальны, тогда как на втором нет точного соотношения параллелей и меридианов с горизонталью и вертикалью: оба являются сложными кривыми.
| Нормальный Меркатор | Поперечный Меркатор | |||
|---|---|---|---|---|
 | \ |  |
На сфере нормаль проходит через центр, и широта (φ), следовательно, соответствует образуемому образуемому в центре на дуга меридиана от экватора до рассматриваемой точки. Если меридианное расстояние ено как m (φ), то
где R обозначает средний радиус земли. Р равно 6 371 км или 3 959 милям. Для получения более точных результатов требуется модель эллипсоида. При этом значении R длина меридиана 1 градуса широты на сфере составляет 111,2 км (69,1 статутных миль) (60,0 морских миль). Длина 1 минуты широты составляет 1,853 км (1,151 статутной мили) (1,00 морская миля), длина 1 секунды широты составляет 30,8 м или 101 фут (см. морская миля ).
В 1687 Исаак Ньютон опубликовал Philosophiæ Naturalis Principia Mathematica, в котором он доказал что вращающееся самогравитирующее жидкое в равновесии принимает форму сплющенного эллипсоида. (В этой статье используется термин эллипсоид, а не более старый термин сфероид.) Результат Ньютона был подтвержден геодезическими измерениями в 18 веке. (См. Дуга меридиана.) Сплюснутый эллипсоид - это трехмерная поверхность, созданная вращением эллипса вокруг его более короткой оси (малой оси). «Сплюснутый эллипсоид вращения» оставшейся части этой статьи сокращенно обозначается словом «эллипсоид». (Эллипсоиды, не имеющие оси симметрии, называются трехосными.)
В истории геодезии использовалось множество различных опорных эллипсоидов. В дни, когда еще не было спутников, они были разработаны для того, чтобы хорошо соответствовать геоиду в ограниченной области съемки, но с появлением GPS стало естественным использованием эталонные эллипсоиды (такие как WGS84 ) с центром в центре масс Земли и малой осью, совмещенной с осью вращения Земли. Эти геоцентрические эллипсоиды обычно находятся в пределах 100 м (330 футов) от геоида. Указание географического положения в данном эллипсоиде отличается: нельзя точно указать широту и долготу географического объекта. Многие карты, поддерживаемые национальными агентствами, основаны на старых эллипсоидах, поэтому необходимо знать, как значения широты и долготы преобразуются из одного эллипсоида в другой. Мобильные устройства GPS включают программное обеспечение для выполнения преобразователей датума, которые связывают WGS84 с локальным опорным эллипсоидом с ним с ним сеткой.
Сфера радиуса a, сжатая вдоль оси z, чтобы сформировать сплюснутый эллипсоид вращения. Форма эллипсоида вращения создается эллипс, который вращается вокруг своей малой (более короткой) оси. Требуются два проекта. Один из них - это неизменно экваториальный радиус, который является большой полуосью , a. Другой параметр обычно (1) полярный радиус или малая полуось, b; или (2) (первое) уплощение, f; или (3) эксцентриситет , эл. Эти параметры не являются независимыми: они связаны с помощью
Многие другие параметры (см. эллипс, эллипсоид ) появляются при изучении геодезии, геофизики и картографических проекций, но все они могут быть выраженными через или два члена а, б, е и д. И f, и e малы и часто появляются в вычислениях в виде разложения в ряды; они порядка 1/298 и 0,0818 соответственно. Значения для ряда эллипсоидов на Рисунки Земли. Справочные эллипсоиды обычно большой полуосью и обратным уплощением 1 / f. Например, определяющие значения для эллипсоида WGS84, используемые всеми устройствами GPS, равны
, из которого получается
Разница между большим и малой полуосями составляет примерно 21 км (13 миль) и как часть большой полуоси равняется уплощению; на мониторе компьютера размер эллипсоида может составлять 300 на 299 пикселей. Его едва ли можно отличить от сферы размером 300 на 300 пикселей, поэтому иллюстрации обычно преувеличивают сглаживание.
Определение геодезической широты () и долготы () на эллипсоиде. Нормаль к поверхности не проходит через центр, за исключением экватора и полюсов. Сетка на эллипсоиде построена точно так же, как на сфере. Нормаль в точке на поверхности эллипсоида не проходит через центр, за исключением точек на экваторе или полюсах, но определение широты остается неизменным как угол между нормалью и экваториальной плоскостью. Терминологию широты необходимо уточнить, выделив:
Важность указания широты опорные данные можно проиллюстрировать на простом примере. На опорный эллипсоид для WGS84, в центре Эйфелевой башни имеет геодезическую широту 48 ° 51 '29 "с.ш., или 48,8583 ° с.ш. и долготы 2 ° 17 '40" в.д. или 2,2944 ° в.д. Те же координаты на опорной точке ED50 определить точку на земле, которая составляет 140 метров (460 футов), удаленные от башни. Веб-поиск может дать несколько разных значений широты башни; эллипсоид ссылки указывается редко.
В дуге меридиана и стандартный текст показано, что расстояние вдоль меридиана от широты φ до экватора определяется выражением (φ в радианах)
где M (φ) - меридиональный радиус кривизны.
Расстояние от экватора до полюса составляет
Для WGS84 это расстояние составляет 10001,965729 км.
Оценка интеграла меридионального расстояния занимает центральное место во многих исследованиях в области геодезии и картографической проекции. Его можно вычислить, расширив интеграл биномиальным рядом и интегрированным членом за членом: подробности см. В Дуга меридиана. Длина дуги меридиана между двумя заданными широтами задается заменой пределов интеграла широтами. Длина небольшой дуги меридиана определяется выражением
| Δ. lat | Δ. long |
|---|---|---|
| 0° | 110,574 км | 111,320 км |
| 15 ° | 110,649 км | 107,550 км |
| 30 ° | 110,852 км | 96,486 км |
| 45 ° | 111,132 км | 78,847 км |
| 60 ° | 111,412 км | 55,800 км |
| 75 ° | 111,618 км | 28,902 км |
| 90 ° | 111,694 км | 0,000 км |
Когда разница широты составляет 1 градус, что соответствует π / 180 радиан, расстояние по дуге составляет примерно
Расстояние в метрах (с точностью до 0,01 метра) между широтами
изменение этого расстояния с широтой (на WGS84 ) показано в таблице вместе с длиной градуса долготы (расстояние с востока на запад):
Калькулятор для любой широты предоставлен Национальным агентством информационной разведки США (NGA).
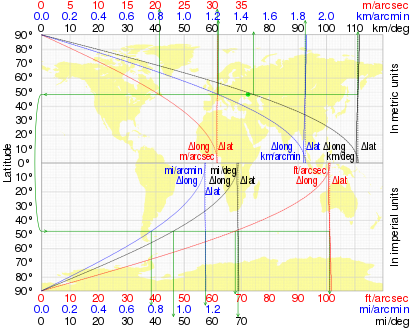
На следующем графике показано изменение градуса широты и градуса долготы с широтой.
Определение геодезической широты (φ) и геоцентрической широты (θ). Исторически морская миля определялась как длина одной угловой минуты по меридиану сферической земли. Модель эллипсоида приводит к изменению морской мили в зависимости от широты. Это было решено путем определения морской мили равной 1852 метрам. Однако для всех практических целей расстояния измеряются по шкале широт на картах. Как Королевская яхтенная ассоциация говорит в своем руководстве для дневных шкиперов : «1 (минута) широты = 1 морская миля», за которой следует «Для большинства практических целей расстояние измеряется от шкала широты, предполагая, что одна минута широты равна одной морской миле ".
Есть шесть вспомогательных широт, которые имеют приложение к специальным задачам в геодезии, геофизике и теория картографических проекций:
определение, приведенное в данном разделе все относится к местоположению на опорный эллипсоиде, но первые два вспомогательных широты, как и геодезической широта, могут быть расширена, чтобы определить трехмерный географическая система координат, как описано ниже. Остальные широты таким образом не используются; они используются только в качестве промежуточных конструкций в карте проекции эллипсоида на плоскости или в расчетах геодезических на эллипсоиде. Их числовые значения не представляют интереса. Например, никому не нужно вычислять подлиннуюшироту Эйфелевой башни.
Приведенные ниже выражения дают вспомогательные широты в терминах геодезической широты, большой полуоси и эксцентриситета e. (Для инверсии см. ниже.) Приведенные формы, помимо вариантов обозначений, относящихся к стандартным справочникам для картографических проекций, именно «Картографические проекции: рабочее руководство» Дж. П. Снайдера. Выводы этих выражений можно найти в Адамсе и онлайн-публикациях Осборна и Раппа.
Определение геодезической широты (φ) и геоцентрической широты (θ). геоцентрическая широта - угол между экваториальной плоскостью и радиусом от центра до точки на поверхности. Связь между геоцентрической широтой (θ) и геодезической широтой (φ) выводится в приведенных выше ссылках как
Геодезическая и геоцентрическая широты равны на экваторе и на полюсах, но на других широтах они отличаются на несколько угловых минут.. Принимая значение квадрата эксцентриситета равным 0,0067 (это зависит от выбора эллипсоида), максимальная разница 
Определение параметрической широты (β) на эллипсоиде. параметрическая или уменьшенная широта, определяется радиусом, проведенным от центра эллипсоида до этой точки Q на сфере окружающей среды (радиуса a), которая является проекцией параллельной оси Земли. точки P на эллипсоиде на широте φ. Он был введен Лежандром и Бесселем, которые решили задачи для геодезических на эллипсоиде, преобразовав их в эквивалентную задачу для сферических геодезических с помощью этой меньшей широты. Обозначение Бесселя u (φ) также используется в современной литературе. Параметрическая широта связана с геодезической широтой следующим образом:
Альтернативное название происходит от параметров уравнения эллипса, описывающего сечение меридиана. В декартовых координатах p, расстояние от малой оси, и z, расстояние над экваториальной плоскостью, уравнение эллипса выглядит следующим образом:
Декартовы координаты точки параметризуются как
Кэли ознаменует собой термическую широта из-за формы этих формул.
параметрическая широта не используется в теории картографических проекций. Его наиболее важное приложение - теория эллипсоидных геодезических (Винсенти, Карни).
Широта выпрямления, μ, - это меридиональное расстояние, масштабированное так, чтобы его на полюсах было равно 90 градусам или π / 2 радиан:
где меридианное расстояние от экватора до широты φ равно (см. Дуга меридиана )
и длина квадранта меридиана от экватора до полюса (полярное расстояние ) составляет
Использование выпрямляющей широты для определения широты в сфере радиуса
имеют проекцию эллипсоида на сферу, такую, что все меридианы, истинную длину и единый масштаб. Затем сфера может быть спроецирована на плоскость с помощью равнопрямоугольной проекции , чтобы получить двойную проекцию от эллипсоида на плоскость, так что все меридианы имеют истинную длину и однородный масштаб меридиана. Пример использования выпрямляющей широты - эквидистантная коническая проекция . (Снайдер, Раздел 16). Выпрямляющая широта также имеет большое значение при построении Поперечной проекции Меркатора.
Ауталической (по-гречески той же области ) широта, ξ, дает сохраняющую площадь преобразование в сферу.
где
![{\ displaystyle {\ begin {align} q (\ phi) = {\ гидроразрыв {\ left (1-e ^ {2} \ right) \ sin \ phi} {1-e ^ {2} \ sin ^ {2} \ phi}} - {\ frac {1-e ^ {2}} {2e}} \ ln \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) \\ [2pt] = {\ frac {\ left (1-e ^ {2} \ right) \ sin \ phi} {1-e ^ {2} \ sin ^ {2} \ phi}} + {\ frac {1-e ^ {2}} {e}} \ tanh ^ {- 1} (e \ грех \ фи) \ конец {выровненный}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b256b2b2f95ca49231dfb329dd724cdbd2de7d1)
и
, а в области внутри страны как
Пример использования аутентичной широты является Коническая проекция равной площади Альберса.
Конформная широта, χ, дает сохраняющее угол (конформное ) преобразование для сферы.
![{\ displaystyle {\ begin {align} \ chi (\ phi) = 2 \ tan ^ {- 1} \ left [\ left ({\ frac {1+ \ sin \ phi} {1- \ sin \ phi}} \ right) \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) ^ {e} \ right] ^ {\ frac {1} {2}} - {\ frac {\ pi} {2}} \\ [2pt ] = 2 \ tan ^ {- 1} \ left [\ tan \ left ({\ frac {\ phi} {2}} + {\ frac {\ pi} {4}} \ right) \ left ({\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right) ^ {\ frac {e} {2}} \ right] - {\ frac {\ pi} {2}} \\ [2pt] = \ tan ^ {- 1} \ left [\ sinh \ left (\ sinh ^ {- 1} (\ tan \ phi) -e \ tanh ^ {- 1} (e \ sin \ phi) \ right) \ right] \\ = \ operatorname {gd} \ left [\ operatorname {gd} ^ {- 1} (\ phi) -e \ tanh ^ { -1} (е \ грех \ фи) \ право] \ конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea5beec16e6a78772ab9d8ffd9123b9ae6e89e0)
где gd (x) - функция Гудермана. (См. Также Проекция Меркатора.)
Конформная широта определяет преобразование эллипсоида в сферу произвольного радиуса, так что угол пересечения между любыми двумя линиями на эллипсоиде одинаков. как соответствующий угол на сфере (чтобы форма мелких элементов хорошо сохранялась). Дальнейшее конформное преобразование сферы в плоскость дает двойную конформную проекцию эллипсоида на плоскость. Это не единственный способ создания такого конформной проекции. Например, «точная» версия поперечной проекции Меркатора на эллипсоиде не является двойной проекцией. (Это, однако, включает обобщение конформной широты на комплексную плоскость).
изометрическая широта, ψ, используется при разработке эллипсоидальных нормальных норм проекции Меркатора и Поперечная проекция Меркатора. Название «изометрический» происходит от того факта, что в любой точке эллипсоида равные приращения ψ и долготы λ вызывают нарушение на равных расстояниях по меридианам и параллелям соответственно. Сетка , определяемая линиями постоянной ψ и постоянной λ, делит поверхность эллипсоида на сетку квадратов (разного размера). Изометрическая широта равна нулю на экваторе, но быстро отклоняется от геодезической широты, стремясь к бесконечности на полюсах. Стандартные обозначения обозначены в книге Снайдера (стр. 15):
![{\ displaystyle {\ begin {align} \ psi (\ phi) = \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ phi} {2}} \ right) \ right] + {\ frac {e} {2}} \ ln \ left [{\ frac {1-e \ sin \ phi} {1 + e \ sin \ phi}} \ right] \\ = \ sinh ^ {- 1} (\ tan \ phi) -e \ tanh ^ {- 1} (e \ sin \ phi) \\ = \ operatorname {gd} ^ {- 1} (\ phi) -e \ tanh ^ {- 1} (e \ sin \ phi). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2999bd8461a831ee601ecad69062c5b30adec5f)
Для нормальной проекции Меркатора (на эллипсоиде) эта функция определяет расстояние между параллелями: если длина экватора на проекции - E (длина длины или пиксели), то расстояние y параллели широты φ от экватора равно
Изометрическая широта ψ соединяет связ с конформной широтой χ:
Формулы в предыдущих разделах дают вспомогательная широта по отношению к геодезической широте. Выражения для геоцентрической и параметрической широт можно инвертировать напрямую, но это невозможно в четырех оставшихся случаях: выпрямляющей, аутентичной, конформной и изометрической широтах. Есть два способа действовать. Первый - это численное обращение определяющего уравнения для каждого отдельного значения дополнительной широты. Доступны следующие методы: итерация с фиксированной точкой и поиск корня Ньютона – Рафсона. Другой, более полезный подход состоит в том, чтобы выразить вспомогательную широту в виде ряда с точки зрения геодезической широты, а затем инвертировать ряд с помощью метода. Такие ряды представлены Адамсом, который использует разложения в ряды Тейлора и дает коэффициенты в терминах эксцентриситета. Осборн выводит ряды в произвольном порядке с помощью пакета компьютерной алгебры Maxima и выражает коэффициенты как с точки зрения эксцентриситета, так и сглаживания. Метод серий не применим к изометрической широте, и необходимо использовать конформную широту на промежуточном этапе.
График справа показывает разницу между геодезической широтой и вспомогательными широтами, кроме изометрической широты (которая расходится до бесконечности на полюсах) для случая WGS84 эллипсоид. На графике показаны различия в угловых минутах. В Северном полушарии (положительные широты) θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ φ; в Южном полушарии (отрицательные широты) неравенства обратные, с равенством на экваторе и полюсах. Хотя график кажется симметричным относительно 45 °, минимумы кривых на самом деле лежат между 45 ° 2 'и 45 ° 6'. Некоторые репрезентативные данные приведены в таблице ниже. Конформные и геоцентрические широты почти неразличимы, и этот факт использовался во времена ручных калькуляторов для ускорения построения картографических проекций.
Для первого порядка сглаживания f вспомогательные широты могут быть выражены как ζ = φ - Cf sin 2φ, где константа C принимает значения [⁄ 2, ⁄ 3, ⁄ 4, 1, 1] для ζ = [β, ξ, μ, χ, θ].
| φ | Параметрическая. β - φ | Authalic. ξ - φ | Исправление. μ - φ | Конформный. χ - φ | Геоцентрический. θ - φ |
|---|---|---|---|---|---|
| 0° | 0.00′ | 0.00′ | 0.00′ | 0,00 ′ | 0,00 ′ |
| 15 ° | −2,88′ | −3,84′ | −4,32′ | -5,76 ′ | −5,76 ′ |
| 30 ° | −5,00′ | −6,66′ | −7,49′ | −9,98 ′ | −9,98 ′ |
| 45 ° | −5,77′ | −7,70′ | −8,66′ | -11,54 ′ | −11,55 ′ |
| 60 ° | −5,00′ | −6,67′ | −7,51′ | -10,01 ′ | −10,02 ′ |
| 75 ° | −2,89′ | −3,86′ | −4,34′ | −5,78 ′ | −5,79 ′ |
| 90 ° | 0,00′ | 0,00′ | 0,00′ | 0,00 ′ | 0.00 |
геодезическая широта, или любой из вспомогательных широт, определенных на эллипсоида, представляет собой с долготой двумерную систему координат на этой эллипсоида. Чтобы определить положение произвольной точки, необходимо расширить такую систему координат до трех измерений. Таким образом используются три широты: геодезическая, геоцентрическая и параметрическая широты используются в геодезических координатах, сферических полярных координатах и эллипсоидальных координатах соответственно.
Геодезические координаты P (ɸ, λ, ч) В произвольной точке Р рассмотрит линию PN, которая является нормальной к эллипсоиду. Геодезические координаты P (ɸ, λ, h) - это широта и долгота точки N на эллипсоиде и расстояние PN. Эта высота отличается от высоты над геоидом или от базовой высоты, например, над средним уровнем моря в указанном месте. Направление PN также будет отличаться от направления вертикального отвеса. Соотношение этих разных высот требует знания формы геоида, а также гравитационного поля Земли.
Геоцентрическая координата, относящаяся к сферическим полярным координатам P (r, θ ′, λ) Геоцентрическая широта θ является дополнением полярного угла θ ′ в традиционном сферическом полярные координаты, в которых координаты точки равны P (r, θ ′, λ), где r - расстояние P от центра O, θ ′ - угол между радиус-вектором и полярной осью, а λ - долгота. Поскольку нормаль в общей точке эллипсоида не проходит через центр, ясно, что точки P 'на нормали, которые имеют одинаковую геодезическую широту, будут иметь разные геоцентрические широты. При исследовании гравитационного поля используются сферические полярные системы координат.
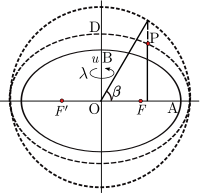Эллипсоидальные координаты P (u, β, λ) Параметрическая широта также может быть расширена до трехмерной системы координат. Для того, чтобы точка Р не на эллипсоид (полуоси ОА и ОВ) построить вспомогательный эллипсоид, который является конфокальным (то же фокусы F, F ') с опорным эллипсоидом: необходимым условием является то, что продукт а.р. большой полуоси и эксцентриситет одинаков для обоих эллипсоидов. Пусть u - малая полуось (OD) вспомогательного эллипсоида. Далее, пусть β - параметрическая широта точки P в дополнительном эллипсоиде. Набор (u, β, λ) определяет координаты эллипсоида. Эти координаты являются естественным выбором в моделях гравитационного поля вращающегося эллипсоидального тела.
Взаимосвязи между вышеуказанными системами координат, а также декартовыми координатами здесь не представлены. Преобразование между геодезическими и декартовыми координатами можно найти в Преобразование географических координат. Связь декартовых и сферических координатных координат задается в Сферической системе координат. Связь декартовых и эллипсоидальных координат обсуждается в Торже.
Астрономическая широта (Φ) - это угол между экваториальной плоскостью и истинным вертикальным направлением в точке на поверхности. Истинная вертикаль, направление отвеса , также является направлением силы тяжести (равнодействующей ускорения свободного падения (на основе массы) и центробежное ускорение ) на этой широте. Астрономическая широта вычисляется по углам, измеренным между зенитом и звездами, склонение точно известно.
В общем случае истинная вертикаль в точке на поверхности не совпадает точно ни с нормалью к эллипсоиду или нормалью к геоиду. Угол между астрономической и геодезической нормалями называется вертикальным отклонением и обычно составляет несколько угловых секунд, но он важен в геодезии. Причина, по которой она отличается от нормали к геоиду, заключается в том, что геоид представляет собой идеализированную теоретическую форму «на среднем уровне моря». Точки на реальной поверхности земли обычно находятся выше или ниже этой идеализированной поверхности геоида, и здесь истинная вертикаль может незначительно отличаться. Кроме того, на истинную вертикаль в определенное время влияет приливные силы, которые усредняет теоретический геоид.
Астрономическую широту не следует путать с склонением, координату астрономы использовать аналогичным образом для определения углового положения звезд к северу / югу от небесный экватор ( см. экваториальные координаты ), ни с эклиптической широтой, координатой, которую астрономы используют для определения углового положения звезд к северу / югу от эклиптики . (см. эклиптические координаты ).
