Войти
Поперечная проекция Меркатора Поперечная проекция Меркатора картографическая проекция адаптация стандартной проекции Меркатора. Поперечная версия широко используется в национальных и международных картографических системах по всему миру, в том числе Универсальная поперечная проекция Меркатора. В сочетании с подходящей геодезической системой координат поперечная проекция Меркатора обеспечивает высокую точность в зонах менее нескольких градусов с востока на запад.
Сравнение касательных и секущих форм нормальной, наклонной и поперечной проекций Меркатора со стандартными параллелями, выделенными красным Поперечная проекция Меркатора - это поперечный аспект стандартной (или нормальной) проекции Меркатора. Они имеют одну и ту же основную математическую конструкцию, и, следовательно, поперечная проекция Меркатора наследует многие черты от нормального Меркатора:
Поскольку центральный меридиан поперечной проекции Меркатора может быть выбран по желанию, его можно использовать для построения высокоточных карт (малой ширины) в любой точке земного шара. Секущая, эллипсоидальная форма поперечной проекции Меркатора - наиболее широко применяемая из всех проекций для точных крупномасштабных карт.
При построении карты на любой проекции, сфера обычно выбирается для моделирования Земли, когда протяженность нанесенной на карту области превышает несколько сотен километров. в длину в обоих измерениях. Для карт меньших регионов необходимо выбрать эллипсоидальную модель , если требуется большая точность; см. следующий раздел. Сферическая форма поперечной проекции Меркатора была одной из семи новых проекций, представленных в 1772 году Иоганном Генрихом Ламбертом. (Текст также доступен в современном английском переводе.) Ламберт не назвал свои прогнозы; название поперечный Меркатор датируется второй половиной девятнадцатого века. Здесь представлены основные свойства поперечной проекции в сравнении со свойствами нормальной проекции.
| Нормальный Меркатор | Поперечный Меркатор | |||
|---|---|---|---|---|
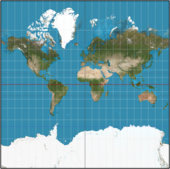 Сферический Нормальный (экваториальный) Меркатор (усеченный по оси y = ± π, что соответствует приблизительно 85 градусам). |  Сферическая поперечная проекция Меркатор (усечено в x = ± π в единицах радиуса Земли). | |||
| • | Центральный меридиан проецируется на прямую x = 0. Другие меридианы проецируются на прямые с постоянной x. | • | Центральный меридиан проецируется на прямую x = 0. Меридианы на 90 градусов к востоку и западу от центрального меридиана переходят к линиям постоянной y через проецируемые полюса. Все остальные меридианы образуют сложные кривые. | |
| • | Экватор проецируется на прямую y = 0, а параллельные окружности переходят в прямые с постоянным y. | • | Экватор проецируется на прямую y = 0, но все остальные параллели представляют собой сложные замкнутые кривые. | |
| • | Спроецированные меридианы и параллели пересекаются под прямым углом. | • | Спроецированные меридианы и параллели пересекаются под прямым углом. | |
| • | Проекция неограничена по оси y. Полюса лежат на бесконечности. | • | Проекция неограничена в направлении x. Точки на экваторе под углом девяноста градусов от центрального меридиана проецируются на бесконечность. | |
| • | Проекция конформная. Хорошо сохранились формы мелких элементов. | • | Проекция конформная. Хорошо сохранились формы мелких элементов. | |
| • | Искажение увеличивается с увеличением y. Проекция не подходит для карт мира. Около экватора искажения небольшие, и проекция (особенно в ее эллипсоидальной форме) подходит для точного картирования экваториальных областей. | • | Искажение увеличивается с увеличением x. Проекция не подходит для карт мира. Около центрального меридиана искажение мало, и проекция (особенно в ее эллипсоидальной форме) подходит для точного картирования узких областей. | |
| • | Гренландия почти такая же большая, как Африка; фактическая площадь составляет примерно одну четырнадцатую площади Африки. | • | Гренландия и Африка находятся недалеко от центрального меридиана; их формы хороши, а соотношение площадей является хорошим приближением к фактическим значениям. | |
| • | Коэффициент шкалы не зависит от направления. Это функция y на проекции. (На сфере это зависит только от широты.) На экваторе шкала верна. | • | Коэффициент шкалы не зависит от направления. Это функция x на проекции. (На сфере это зависит и от широты, и от долготы.) Масштаб соответствует центральному меридиану. | |
| • | Проекция достаточно точна около экватора. Масштаб на угловом расстоянии 5 ° (по широте) от экватора менее чем на 0,4% больше, чем масштаб на экваторе, и примерно на 1,54% больше на угловом расстоянии 10 °. | • | Проекция достаточно точна около центрального меридиана. Масштаб на угловом расстоянии 5 ° (по долготе) от центрального меридиана менее чем на 0,4% больше, чем масштаб на центральном меридиане, и составляет около 1,54% на угловом расстоянии 10 °. | |
| • | В секущей версии масштаб уменьшен на экваторе, и это верно для двух линий, параллельных проецируемому экватору (и соответствующих двум параллельным окружностям на сфере). | • | В секущей версии масштаб уменьшен по центральному меридиану, и это верно по двум линиям, параллельным проектируемому центральному меридиану. (Эти две линии не являются меридианами.) | |
| • | Конвергенция (угол между проецируемыми меридианами и линиями сетки с постоянной x) идентично нулю. Север сетки и истинный север совпадают. | • | Сходимость равна нулю на экваторе и отлична от нуля везде. Он увеличивается по мере приближения к полюсам. Сеточный север и истинный север не совпадают. | |
| • | Прямые линии (постоянного азимута на сфере) переходят в прямые. |
Эллипсоидальная форма поперечной проекции Меркатора была разработана Карлом Фридрихом Гауссом в 1825 году и затем проанализирована Иоганном Генрихом Луи Крюгером в 1912 году. Проекция известна под несколькими названиями: конформная проекция Гаусса или Гаусса-Крюгера в Европе; поперечный Меркатор в США; или поперечный Меркатор Гаусса-Крюгера вообще. Проекция соответствует постоянному масштабу на центральном меридиане. (Существуют и другие конформные обобщения поперечной проекции Меркатора от сферы до эллипсоида, но только Гаусс-Крюгер имеет постоянный масштаб на центральном меридиане.) На протяжении двадцатого века поперечная проекция Меркатора Гаусса-Крюгера принималась в той или иной форме, многими странами (и международными организациями); кроме того, он служит основой для серии проекций Универсальной поперечной проекции Меркатора. Проекция Гаусса – Крюгера в настоящее время является наиболее широко используемой проекцией в точном крупномасштабном картографировании.
Проекция, разработанная Гауссом и Крюгером, была выражена в терминах степенных рядов низкого порядка, которые, как предполагалось, расходились в направление восток-запад, как в сферическом варианте. Это было доказано британским картографом Э. Х. Томпсоном, чья неопубликованная точная (закрытая форма) версия проекции, представленная Л. П. Ли в 1976 г., показала, что эллипсоидальная проекция конечна (см. Ниже). Это наиболее разительное различие между сферической и эллипсоидальной версиями поперечной проекции Меркатора: Гаусс-Крюгер дает разумную проекцию всего эллипсоида на плоскость, хотя его основное применение - точное крупномасштабное картографирование «близко» к центральной проекции. меридиан.
Эллипсоидальная поперечная проекция Меркатора: конечная проекция. В большинстве приложений система координат Гаусса-Крюгера применяется к узкой полосе около центральных меридианов, где разности между сферической и эллипсоидальной версиями малы, но тем не менее важны для точного картирования. Прямые ряды для масштаба, сходимости и искажения являются функциями эксцентриситета, а также широты и долготы на эллипсоиде: обратные ряды являются функциями эксцентриситета, а также x и y на проекции. В секущей версии линии истинного масштаба на проекции больше не параллельны центральному меридиану; они слегка изгибаются. Угол схождения между проецируемыми меридианами и линиями постоянной сетки x больше не равен нулю (кроме экватора), так что азимут сетки должен быть скорректирован для получения азимута от истинного севера. Разница небольшая, но заметная, особенно в высоких широтах.
В своей статье 1912 года Крюгер представил два различных решения, отличающихся здесь параметром расширения:
Серия Крюгера-λ была первой, которая была реализована, возможно, потому, что их было намного легче вычислить на ручных калькуляторах середины двадцатого века.
Серия Krüger-n была реализована (до четвертого порядка по n) следующие нации.
Версии серии Krüger – n более высокого порядка были реализованы Энсагером и Подером до седьмого порядка и до десятого. заказ Кавасэ. Помимо расширения ряда для преобразования между широтой и конформной широтой, Карни реализовал ряд до тридцатого порядка.
Точное решение EH Томпсон описан Л. П. Ли. Он построен в терминах эллиптических функций (определенных в главах 19 и 22 справочника NIST), которые могут быть вычислены с произвольной точностью с помощью алгебраических вычислительных систем, таких как Maxima. Такая реализация точного решения описана Karney (2011).
Точное решение является ценным инструментом для оценки точности усеченных рядов n и λ. Например, исходная серия Krüger – n 1912 года очень выгодно отличается от точных значений: они отличаются менее чем на 0,31 мкм в пределах 1000 км от центрального меридиана и менее чем на 1 мм в пределах 6000 км. С другой стороны, разница между серией Redfearn, используемой Geotrans, и точным решением составляет менее 1 мм с разницей в долготе в 3 градуса, что соответствует расстоянию 334 км от центрального меридиана на экваторе, но всего 35 км на северной границе зоны UTM. Таким образом, серия Krüger – n намного лучше, чем серия Redfearn λ.
Серия Redfearn становится намного хуже по мере расширения зоны. Карни приводит в качестве поучительного примера Гренландию. Длинный тонкий массив суши сосредоточен на высоте 42 Вт и в самой широкой точке находится не более чем на 750 км от этого меридиана, в то время как размах по долготе достигает почти 50 градусов. Krüger-n имеет точность в пределах 1 мм, но версия Redfearn серии Krüger-λ имеет максимальную погрешность 1 километр.
Собственная серия Карни 8-го порядка (по n) имеет точность до 5 морских миль в пределах 3900 км от центрального меридиана.
Нормальный аспект касательной цилиндрической проекции сферы Нормальные цилиндрические проекции описываются по отношению к цилиндру тангенциальный на экваторе с осью вдоль полярной оси сферы. Цилиндрические проекции построены так, что все точки меридиана проецируются в точки с x = aλ и y как заданной функцией φ. Для касательной нормальной проекции Меркатора (единственные) формулы, которые гарантируют конформность, следующие:
![{\ displaystyle x = a \ lambda \,, \ qquad y = a \ ln \ left [\ tan \ left ({\ frac {\ pi} {4}} + {\ frac {\ varphi} {2}} \ right) \ right ] = {\ frac {a} {2}} \ ln \ left [{\ frac {1+ \ sin \ varphi} {1- \ sin \ varphi}} \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47d199db07fc6cb9a3994a7f82e29c99382ca7dd)
Соответствие означает, что шкала , k, не зависит от направления: это функция только широты:
Для секущей версии проекции в правой части всех этих уравнений есть коэффициент k 0 : это гарантирует, что масштаб равен k 0 на экваторе.
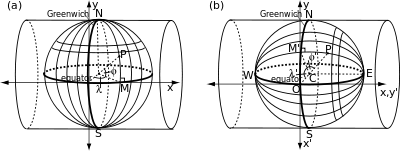Поперечные меркаторные сетки На рисунке слева показано, как поперечный цилиндр соотносится с традиционной сеткой на сфере. Он касается некоторого произвольно выбранного меридиана, а его ось перпендикулярна оси сферы. Оси x и y, определенные на рисунке, относятся к экватору и центральному меридиану точно так же, как и для нормальной проекции. На рисунке справа повернутая сетка связана с поперечным цилиндром так же, как нормальный цилиндр связан со стандартной сеткой. «Экватор», «полюса» (E и W) и «меридианы» повернутой координатной сетки отождествляются с выбранным центральным меридианом, точки на экваторе под углом 90 градусов к востоку и западу от центрального меридиана и большие круги через эти точки.
Поперечная геометрия меркатора Положение произвольной точки (φ, λ) на стандартной координатной сетке также можно определить по углам на повернутой координатной сетке: φ ′ (угол M′CP) - эффективная широта и −λ ′ (угол M′CO) становится эффективной долготой. (Знак минус необходим для того, чтобы (φ ′, λ ′) были связаны с повернутой сеткой так же, как (φ, λ) связаны со стандартной сеткой). Декартовы оси (x ', y') связаны с повернутой координатной сеткой так же, как оси (x, y) связаны со стандартной сеткой.
Касательная поперечная проекция Меркатора определяет координаты (x ′, y ′) через −λ ′ и φ ′ по формулам преобразования касательной нормальной проекции Меркатора:
![{\displaystyle x'=-a\lambda '\,\qquad y'={\frac {a}{2}}\ln \left[{\frac {1+\sin \varphi '}{1-\sin \varphi '}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ec29e50c7aa771e9e79688ca1207e26663b4e2e)
Это преобразование проецирует центральный меридиан в прямую линию конечной длины и в то же время проецирует большие круги через E и W (которые включают экватор) в бесконечные прямые, перпендикулярные к центральному меридиану. Истинные параллели и меридианы (кроме экватора и центрального меридиана) не имеют простого отношения к повернутой координатной сетке и проецируются на сложные кривые.
Углы двух координатных сеток связаны с помощью сферической тригонометрии на сферическом треугольнике NM'P, определяемом истинным меридианом через начало координат, OM′N, истинный меридиан, проходящий через произвольную точку, MPN, и большой круг WM′PE. Результат:
Прямые формулы, задающие декартовы координаты (x, y), непосредственно следуют из вышеизложенного. Установка x = y ′ и y = −x ′ (и восстанавливающие коэффициенты k 0 для учета версий секущих)
![{\ displaystyle {\ begin {align} x (\ lambda, \ varphi) = {\ frac {1} {2}} k_ {0} a \ ln \ left [{\ frac {1+ \ sin \ lambda \ cos \ varphi} {1- \ sin \ lambda \ cos \ varphi} } \ right], \\ [5px] y (\ lambda, \ varphi) = k_ {0} a \ arctan \ left [\ sec \ lambda \ tan \ varphi \ right], \ end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6980ee67020617f53a986c6eeb5d7af266381d9)
Вышеупомянутые выражения даны у Ламберта, а также (без производных) у Снайдера, Малинга и Осборна (с полной информацией).
Обращение приведенных выше уравнений дает
![{\ displaystyle {\ begin {align} \ lambda (x, y) = \ arctan \ left [\ sinh {\ frac {x} {k_ {0}] a}} \ sec {\ frac {y} {k_ {0} a}} \ right], \\ [5px] \ varphi (x, y) = \ arcsin \ left [{\ t_dv {sech}} \ ; {\ frac {x} {k_ {0} a}} \ sin {\ frac {y} {k_ {0} a}} \ right]. \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d79354a0dad109450479ec16db488ad896d6d810)
В терминах координат относительно повернутой сетки коэффициент шкалы задается как k = sec φ ′: это может быть выражено либо в географических координатах, либо в координатах проекции:
![{\ displaystyle {\ begin {выровнено} k (\ lambda, \ varphi) = {\ frac {k_ {0}} {\ sqrt {1- \ sin ^ {2} \ lambda \ cos ^ {2} \ varphi}}}, \\ [5px] k (x, y) = k_ {0} \ cosh \ left ({\ frac {x} {k_ {0} a}} \ right). \ конец {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f258c8b8bf11cd3f37adf8a4d2372b9c9ea58b5a)
Второе выражение показывает, что масштабный коэффициент - это просто функция расстояния от центрального меридиана проекции. Типичное значение масштабного коэффициента k 0 = 0,9996, так что k = 1, когда x составляет приблизительно 180 км. Когда x составляет приблизительно 255 км и k 0 = 1.0004: масштабный коэффициент находится в пределах 0,04% от единицы на полосе шириной около 510 км.
Угол конвергенции Угол конвергенции γ в точке проекции определяется углом, измеренным от проецируемого меридиана, определяющего истинный север, до линии сетки с постоянным x, определяющей сетку к северу. Следовательно, γ положительно в квадранте к северу от экватора и к востоку от центрального меридиана, а также в квадранте к югу от экватора и к западу от центрального меридиана. Схождение необходимо добавить к азимуту сетки, чтобы получить пеленг от истинного севера. Для секущей поперечной проекции Меркатора сходимость может быть выражена либо через географические координаты, либо через координаты проекции:
![{\ displaystyle {\ begin {align} \ gamma (\ lambda, \ varphi) = \ arctan (\ tan \ lambda \ sin \ varphi), \\ [5px] \ gamma (x, y) = \ arctan \ left ( \ tanh {\ frac {x} {k_ {0} a}} \ tan {\ frac {y} {k_ {0} a}} \ right). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4770e247d333c3a92fb819ff8d133cd20555aca0)
Подробная информация о фактических реализациях
Координаты проекции, полученные в результате различных изменений эллипсоидальной поперечной проекции Меркатора, являются декартовыми координатами, так что центральный меридиан соответствует оси x, а экватор соответствует оси y. И x, и y определены для всех значений λ и ϕ. Проекция не определяет сетку: сетка - это независимая конструкция, которую можно определить произвольно. На практике национальные реализации и UTM действительно используют сетки, выровненные с декартовыми осями проекции, но они имеют конечную протяженность, а начало координат не обязательно должно совпадать с пересечением центрального меридиана с экватором.
Истинное начало координат сетки всегда берется на центральном меридиане, поэтому координаты сетки будут отрицательными к западу от центрального меридиана. Чтобы избежать таких отрицательных координат сетки, стандартная практика определяет ложное начало к западу (и, возможно, к северу или югу) от начала координатной сетки: координаты относительно ложного начала координат определяют восток и северное положение, которое всегда будет положительным. ложное восточное положение, E 0, это расстояние истинного начала координат сетки к востоку от ложного начала координат. ложное северное положение, N 0, это расстояние истинного начала координат сетки к северу от ложного начала координат. Если истинное начало координатной сетки находится на широте φ 0 на центральном меридиане, а масштабный коэффициент центрального меридиана равен k 0, то эти определения дают восточные и северные координаты следующим образом:
![{ \ displaystyle {\ begin {align} E = E_ {0} + x (\ lambda, \ varphi), \\ [5px] N = N_ {0} + y ( \ lambda, \ varphi) -k_ {0} m (\ varphi _ {0}). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5997ecfc3a32bb9e82de6f4bd072d94be55e496)
Термины "восток" и "север" не означают строго направления на восток и север. Линии сетки поперечной проекции, кроме осей x и y, не проходят с севера на юг или с востока на запад, как это определено параллелями и меридианами. Это очевидно из представленных выше глобальных прогнозов. Вблизи центрального меридиана различия небольшие, но измеримые. Разница между линиями сетки север-юг и истинными меридианами - это угол конвергенции.
 | На Wikimedia Commons есть материалы, связанные с проекциями Меркатора. |
