Система координат, которая определяет точками, а не днями

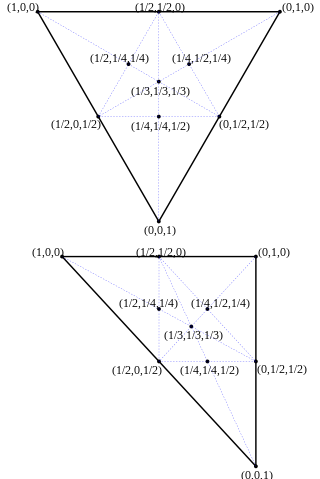
3-симплексная система с барицентрическими подразделениями 1-граней (ребер) 2-гранями (треугольники) и 3-гранями (тело).
В геометрии барицентрическая система координат является системой координат, в которой местоположение точки указывается на симплекс (треугольник для точек в плоскости , тетраэдр для точек в трехмерное пространство и т. Д.). барицентрические координаты точки можно интерпретировать как массы, размещенные в вершинах симплекса, так что точка является центром масс (или барицентром) этих масс. Эти массы могут быть нулевыми или отрицательными; все они положительны тогда и только тогда, когда точка находится внутри симплекса.
Каждая точка имеет барицентрические координаты, и их сумма не равна нулю. Два кортежа барицентрических координат задают одну и ту же точку тогда и только тогда, когда они регулируют; то есть, если один кортеж может быть получен путем умножения элементов другого кортежа на такое же ненулевое число. Следовательно, барицентрические координаты считаются либо определенными от до умножением на ненулевую константу, либо нормализованными для суммирования до единицы.
Барицентрические координаты были введены Августом Фердинандом Мёбиус в 1827 году. Это особые однородные координаты. Барицентрические координаты сильно связаны с декартовыми координатами и, в более общем смысле, с аффинными координатами (см. Аффинное пространство § Связь между барицентрическими и аффинными координатами ).
Барицентрические координаты особенно полезны в геометрии треугольника для изучения свойств, которые не зависят от углового треугольника, таких как теорема Чевы. В автоматизированном проектировании они полезны для определенного вида поверхности Безье.
Содержание
- 1 Определение
- 2 Связь с декартовыми или аффинными координатами
- 3 Связь с проективные координаты
- 4 Барицентрические координаты на треугольниках
- 4.1 Преобразование между барицентрическими и декартовыми координатами
- 4.2 Преобразование между барицентрическими и трилинейными координатами
- 4.3 Уравнения в барицентрических координатах
- 4.4 Расстояние между точками
- 4.5 Приложения
- 4.5. 1 Определение местоположения относительно треугольника
- 4.5.2 Интерполяция на треугольной неструктурированной сетке
- 4.5.3 Интегрирование по треугольнику или тетраэдру
- 4.6 Примеры особых точек
- 5 Барицентрический координаты на тетраэдрах
- 6 Обобщенные барицентрические координаты
- 7 См. также
- 8 Ссылки
- 9 Внешние ссылки
- 10 Внешние ссылки
Определение
Пусть  быть n + 1 балл i na евклидово пространство, плоское или аффинное пространство
быть n + 1 балл i na евклидово пространство, плоское или аффинное пространство  размерности аффинно-независимой ; это означает, что не существует аффинного подпространства размерности n, которое содержит все точки, или, что то же самое, определяет симплекс. Для любой точки
размерности аффинно-независимой ; это означает, что не существует аффинного подпространства размерности n, которое содержит все точки, или, что то же самое, определяет симплекс. Для любой точки  существует scalars
существует scalars  , которые не все равны нулю, такие, что
, которые не все равны нулю, такие, что

для любой точки O. (Как обычно, запись  представляет вектор перемещения или свободный вектор, который отображает точку в точку B.)
представляет вектор перемещения или свободный вектор, который отображает точку в точку B.)
Элементы (n + 1) кортежа  , который удовлетворяет уравнению, называются барицентрическими координатами P относительно
, который удовлетворяет уравнению, называются барицентрическими координатами P относительно  Использование двоеточий в обозначении кортежа означает, что барицентрические координаты являются основой своего рода однородными координатами, то есть точка не соответствует, если все координаты умножаются на одну и ту же ненулевую константу. Более того, барицентрические координаты не изменяются, если вспомогательная точка O, начало координат, изменяется.
Использование двоеточий в обозначении кортежа означает, что барицентрические координаты являются основой своего рода однородными координатами, то есть точка не соответствует, если все координаты умножаются на одну и ту же ненулевую константу. Более того, барицентрические координаты не изменяются, если вспомогательная точка O, начало координат, изменяется.
Барицентрические координаты точки уникальны от до и масштабирования. То есть два кортежа  и
и  являются барицентрическими координатами той же точки тогда и только тогда, когда существует ненулевой скаляр
являются барицентрическими координатами той же точки тогда и только тогда, когда существует ненулевой скаляр  такой, что
такой, что  для каждого i.
для каждого i.
В некоторых случаях полезно сделать уникальные барицентрические координаты точки. Это получается путем наложения условий

или, что эквивалентно, путем деления каждого  на сумму всех
на сумму всех  Эти обычные барицентрические координаты называются нормализованными или абсолютными барицентрическими координатами . Иногда их также называют аффинными координатами, хотя этот термин обычно относится к нескольким иному понятию.
Эти обычные барицентрические координаты называются нормализованными или абсолютными барицентрическими координатами . Иногда их также называют аффинными координатами, хотя этот термин обычно относится к нескольким иному понятию.
Иногда это нормализованные барицентрические координаты, которые называют барицентрическими координатами. В этом случае выше координаты называются однородными барицентрическими координатами.
В приведенных выше обозначениях все однородные барицентрические координаты A i равны нулю, за исключением индекса индекс i. При работе с вещественными числами (приведенное выше определение используется для аффинных пространств произвольным полем ) точки, все нормализованные барицентрические координаты которых неотрицательны, образуют выпуклую оболочку из  который является симплекс, имеющий эти точки в качестве вершин.
который является симплекс, имеющий эти точки в качестве вершин.
В приведенных выше обозначениях кортеж  такой, что
такой, что

не определяет никакую точку, но вектор

не зависит от начала O. Направление направления этого вектора не изменяется, если все  умножаются на один и тот же скаляр, однородный кортеж
умножаются на один и тот же скаляр, однородный кортеж  определить направление линий, то есть бесконечно удаленную точку. Подробности смотрите ниже.
определить направление линий, то есть бесконечно удаленную точку. Подробности смотрите ниже.
Связь с декартовыми или аффинными координатами
Барицентрические координаты сильно связаны с декартовыми координатами и, в более общем смысле, аффинными координатами. Для пространства размерности n эти системы координат относительно точки O, координаты начала координат, координаты начала координат  , координаты которых равны нулю, за исключением индекса i, равного единице.
, координаты которых равны нулю, за исключением индекса i, равного единице.
Точка имеет координаты

для такой системы координат тогда и только тогда. если его нормализованные барицентрические координаты равны

относительно точек 
Основным преимуществом барицентрических систем координат является симметричность относительно n + 1 определяющих точек. Поэтому они часто полезны для изучения свойств, симметричных относительно n + 1 точки. С другой стороны, расстояния и углы трудно выразить в общих барицентрических системах координат, и когда они задействованы, обычно проще использовать декартову систему координат.
Связь с проективными координатами
Однородные барицентрические координаты также сильно связаны с некоторыми проективными координатами. Однако эта взаимосвязь более тонкая, чем в случае аффинных координат, и для ясного понимания бескординатного определения проективного завершения аффинного пространства и определение проективного фрейма.
Проективное завершение аффинного пространства размерности n - это проективное пространство той же размерности, которое содержит аффинное пространство как дополнение гиперплоскость. Проективное пополнение единственно до и изоморфизма. Гиперплоскость называется гиперплоскостью на бесконечности, а ее точками являются бесконечно удаленные точки аффинного пространства.
Учитывая проективное пространство размерности n, проективное кадр - это упорядоченный набор из n + 2 точек, не лежащих в одной гиплоерпскости. Проективный фрейм определяет проективную систему координат, в которой все координаты (n + 2) -й точки фрейма равны, а в противном случае все координаты i-й точки равны нулю, кроме i-й.
При построении проективного пополнения из аффинной системы координат обычно определяют его относительно проективной системы координат, состоящей из пересечений с гиперплоскостью на бесконечности координатных осей , начала аффинного, и точки, у которой все аффинные координаты равны единице. Это означает, что точка на бесконечности имеет последнюю координату, равную нулю, и что проективные координаты точки аффинного пространства получаются дополнением ее аффинных координатей в качестве (n + 1) -й координаты.
Если имеется n + 1 точка в аффинном пространстве, определяющая барицентрическую систему координат, это еще один проективный каркас проективного пополнения, который удобно выбирать. Эта рамка состоит из этих точек и их центроида, то есть есть точки, у которых все барицентрические координаты равны. В этом случае однородные барицентрические точки в аффинном пространстве совпадают с проективными этими точками. Точка находится на бесконечности тогда и только тогда, когда сумма ее координаты равна нулю. Эта точка находится в направлении вектора, определенного в конце § Определение.
.
Барицентрические координаты на треугольниках
Барицентрические координаты

в равностороннем треугольнике и в прямоугольном треугольнике.
В контексте треугольника, барицентрические координаты также известны как координаты области или координаты площади, поскольку координаты P относительно треугольника ABC эквивалентны (знаковым) отношениям площадей PBC, PCA и PAB к площади справочного треугольника ABC. Площадные и трилинейные координаты используются в геометрии для аналогичных целей.
Барицентрические или площадные координаты полезны в инженерных приложениях, включающие треугольные подобласти. Это упрощает вычисление аналитических интегралов, а квадратурные таблицы Гаусса часто представляет в терминах координат области.
Рассмотрим треугольник  , определяемый его тремя вершинами,
, определяемый его тремя вершинами,  ,
,  и
и  . Каждую точку
. Каждую точку  , расположенную внутри этого треугольника, можно записать как уникальную выпуклую комбинацию трех вершин. Другими словами, для каждого
, расположенную внутри этого треугольника, можно записать как уникальную выпуклую комбинацию трех вершин. Другими словами, для каждого  существует уникальная последовательность из трех чисел,
существует уникальная последовательность из трех чисел,  такие, что
такие, что  и
и

Три числа  указывают «барицентрические» или «площадные» координаты точки
указывают «барицентрические» или «площадные» координаты точки  относительно треугольника. Их часто обозначают как
относительно треугольника. Их часто обозначают как  вместо
вместо  . Обратите внимание, что хотя есть три координаты, есть только две степени свободы, поскольку
. Обратите внимание, что хотя есть три координаты, есть только две степени свободы, поскольку  . Таким образом, каждая точка однозначно определяет любыми двумя барицентрическими координатами.
. Таким образом, каждая точка однозначно определяет любыми двумя барицентрическими координатами.
Чтобы объяснить, почему эти координаты являются знаковыми отношениями предположим, что мы работаем в евклидовом пространстве  . Рассмотрим здесь декартову систему координат
. Рассмотрим здесь декартову систему координат  и связанную с ней базис, а именно
и связанную с ней базис, а именно  . Рассмотрим также положительно ориентированный треугольник
. Рассмотрим также положительно ориентированный треугольник  , лежащий в
, лежащий в  плоскости. Известно, что для любого basis
плоскости. Известно, что для любого basis  из
из  и любой свободный вектор
и любой свободный вектор  один имеет
один имеет
![{\ displaystyle \ mathbf {h} = {\ frac {1} {(\ mathbf {e}, \ mathbf {f}, \ ma thbf {g})}} \ cdot \ left [(\ mathbf {h}, \ mathbf {f}, \ mathbf {g}) \ mathbf {e} + (\ mathbf {e}, \ mathbf {h}, \ mathbf {g}) \ mathbf {f} + (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) \ mathbf {g} \ right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1318f42d7c5bac15a253331f26a3a18a519e45)
где  обозначает смешанное произведение этих трех векторов.
обозначает смешанное произведение этих трех векторов.
Возьмем  , где
, где  - произвольная точка на плоскости
- произвольная точка на плоскости  , и обратите внимание, что
, и обратите внимание, что

Тонкий момент относительно нашего выбора векторов:  фактически является классом эквиполентности связанного вектора
фактически является классом эквиполентности связанного вектора  .
.
Мы получили, что

Учитывая положительную (против часовой стрелки ) ориентацию треугольника  , знаменатель обоих
, знаменатель обоих  и
и  - это в точности удвоенная площадь треугольника
- это в точности удвоенная площадь треугольника  . Кроме того,
. Кроме того,

и поэтому числители из  и
и  - это двойники подписанных областей треугольников
- это двойники подписанных областей треугольников  и соответственно
и соответственно  .
.
Далее, мы заключаем, что

что означает, что число  ,
,  и
и  - барицентрические координаты
- барицентрические координаты  . Аналогично, третья барицентрическая координата читается как
. Аналогично, третья барицентрическая координата читается как

Это  -буквенное обозначение барицентрические координаты происходит из того факта, что точка
-буквенное обозначение барицентрические координаты происходит из того факта, что точка  может интерпретироваться как центр масс для масс
может интерпретироваться как центр масс для масс  ,
,  ,
,  , которые защищены в
, которые защищены в  ,
,  и
и  .
.
Переключение между барицентрическими координатами и другими системами координат значительно упрощает решение некоторых проблем.
Преобразование между барицентрическими и декартовыми координатами
Учитывая точку  в плоскости треугольника, можно получить барицентрические координаты
в плоскости треугольника, можно получить барицентрические координаты  ,
,  и
и  из декартовых координат
из декартовых координат  или наоборот.
или наоборот.
Мы можем записать декартовы координаты точки  через декартовы компоненты вершин треугольника
через декартовы компоненты вершин треугольника  ,
,  ,
,  где
где  и в терминах барицентрических координат
и в терминах барицентрических координат  как
как

То есть декартовы координаты любой точки представляют собой средневзвешенное значение декартовых вершин треугольника, при этом весе единицы барицентрические координаты точки, суммируемые с единицей.
Чтобы найти обратное преобразование декартовой системы координат в барицентрической системе, мы сначала подставляем  в приведенном выше примере, чтобы получить
в приведенном выше примере, чтобы получить

Перестановка, это

Это линейное преобразование может быть записано более кратко как

где  - это вектор первых двух барицентрических координат,
- это вектор первых двух барицентрических координат,  - вектор из декартовых координат, а
- вектор из декартовых координат, а  - матрица, заданная как
- матрица, заданная как

Теперь матрица  обратимая, поскольку
обратимая, поскольку  и
и  являются линейно независимыми (если бы это было не так, то
являются линейно независимыми (если бы это было не так, то  ,
,  и
и  будет коллинеарен и не будет формироваться при треугольник). Таким образом, мы можем изменить приведенное выше уравнение, чтобы получить
будет коллинеарен и не будет формироваться при треугольник). Таким образом, мы можем изменить приведенное выше уравнение, чтобы получить

Нахождение барицентрических координат таким образом, сводится к нахождению 2 × 2 обратной матрицы для  , простые задачи.
, простые задачи.
В явном виде формулы для барицентрических координат точки  в терминах ее декартовых координат (x, y) и в терминах декартовы координаты вершин треугольника :
в терминах ее декартовых координат (x, y) и в терминах декартовы координаты вершин треугольника :



Другой способ решить преобразование декартовых координат в барицентрические - это переписать задачу в матрице сформируйте так, чтобы

с  и
и  . Тогда условие
. Тогда условие  читает
читает  и барицентрические координаты могут быть решенными как решение линейной системы
и барицентрические координаты могут быть решенными как решение линейной системы

Преобразование между барицентрическими и трилинейными координатами
Точка с трилинейными координатами x: y: z имеет барицентрические координаты оси: по: cz, где a, b, c - длина сторон треугольника. И наоборот, точка с барицентрикой  имеет трилинейные линии
имеет трилинейные линии 
Уравнения в барицентрических координатах
Стороны a, b, c соответственно имеют уравнения

Уравнение треугольника прямой Эйлера is

Используя ранее данное преобразование между барицентрическими и трилинейными координатами, различные другие уравнения, приведенные в Трилинейные координаты # Формулы могут быть переписаны в терминах барицентрических координат.
Расстояние между точками
Вектор с территории двух нормализованных точек  и
и  is
is

Расстояние  между
между  и
и  , или длина вектора с ущерба
, или длина вектора с ущерба  is
is
![{\ displaystyle d ^ {2} = \ left | PQ \ right | ^ {2} = - a ^ {2} yz-b ^ {2} zx-c ^ {2} xy = {\ frac {1} {2}} [x ^ {2} (b ^ {2} + c ^ {2} -a ^ {2}) + y ^ {2} (c ^ {2} + a ^ {2} -b ^ {2}) + z ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc8615c8fe62884423e5e671a2b1a4cf5cd145ad)
где a, b, c длина - сторон треугольника. Эквивалентность двух последних выражений следует из  , которое выполняется, потому что
, которое выполняется, потому что 
Барицентрические координаты точки можно вычислить на основе расстояний d i до трех вершин треугольника решения уравнения

Приложения

Два решения 8, 5 и 3 л
заливка воды с использованием барицентрического графика. Желтая область обозначает комбинации, достижимые с кувшинами. Сплошные красные и пунктирные синие пути показывают текучие переходы. Когда вершина попадает в пунктирный треугольник, было измерено 4 л.
Определение местоположения относительно треугольника
Хотя барицентрические координаты чаще всего используются для обработки точек внутри треугольника, их также можно использовать для описания точки вне треугольника. Используемая здесь точка не находится внутри треугольника, используя приведенные выше формулы для вычисления барицентрической системы координат. Однако, поскольку точка находится за пределами треугольника, по крайней мере одна из координат нарушит наше исходное предположение, что  . Фактически для любой точки в декартовых координатах мы можем использовать этот факт, чтобы определить, где эта точка находится относительно треугольника.
. Фактически для любой точки в декартовых координатах мы можем использовать этот факт, чтобы определить, где эта точка находится относительно треугольника.
Если точка лежит внутри треугольника, все барицентрические координаты лежат в открытом интервале  Если точка лежит на краю треугольника, но не в вершине, одна из координат области
Если точка лежит на краю треугольника, но не в вершине, одна из координат области  (тот, который связан с противоположной вершиной) равенство нулю, а два других лежат в открытом интервале
(тот, который связан с противоположной вершиной) равенство нулю, а два других лежат в открытом интервале  Если точка лежит на вершине, связанная с этой вершиной, равна 1, а остальные равны нулю. Наконец, если точка лежит вне треугольника, по крайней мере одна координата отрицательна.
Если точка лежит на вершине, связанная с этой вершиной, равна 1, а остальные равны нулю. Наконец, если точка лежит вне треугольника, по крайней мере одна координата отрицательна.
Подводя итог,
- Точка
 лежит внутри треугольника тогда и только тогда, когда
лежит внутри треугольника тогда и только тогда, когда  .
.  лежит на краю или углу треугольника, если
лежит на краю или углу треугольника, если  и
и  .
.
- В случае опасности
 лежит вне треугольника.
лежит вне треугольника.
В частности, если точка лежит на противоположной стороне боковой линии от вершины, противоположной боковой линии, то барицентрическая координата этой точки, соответствующей этой вершине, отрицательна.
Интерполяция на треугольной неструктурированной сетке

Поверхность (верхняя часть), полученная в результате линейной интерполяции по заданной треугольной сетке (нижняя часть) в плоскости x, y. Поверхность аппроксимирует функцию z = f (x, y), учитывая только значения f в вершинах сетки.
Если  - известные величины, но значения
- известные величины, но значения  внутри треугольника, определенного как
внутри треугольника, определенного как  неизвестно, их можно аппроксимировать с помощью линейной интерполяции. Барицентрические координаты использовать удобный способ вычисления этой интерполяции. Если
неизвестно, их можно аппроксимировать с помощью линейной интерполяции. Барицентрические координаты использовать удобный способ вычисления этой интерполяции. Если  - точка внутри треугольника с барицентрическими координатами
- точка внутри треугольника с барицентрическими координатами  ,
,  ,
,  , тогда
, тогда

В общем, для любой неструктурированной сетки или многоугольная сетка, этот вид техники можно использовать для аппроксимации значения  во всех точках, если значение функции известно во всех вершинах сетка. В этом случае у нас есть много треугольников, каждый из которых соответствует разной части пространства. Чтобы интерполировать функцию
во всех точках, если значение функции известно во всех вершинах сетка. В этом случае у нас есть много треугольников, каждый из которых соответствует разной части пространства. Чтобы интерполировать функцию  в точке
в точке  , сначала необходимо найти треугольник, содержащий
, сначала необходимо найти треугольник, содержащий  . Для этого
. Для этого  преобразуется в барицентрические координаты каждого треугольника. Если найден некоторый треугольник, координаты которого удовлетворяют
преобразуется в барицентрические координаты каждого треугольника. Если найден некоторый треугольник, координаты которого удовлетворяют  , то точка лежит в этом треугольнике или на его краю (объяснено в предыдущем разделе). Затем значение
, то точка лежит в этом треугольнике или на его краю (объяснено в предыдущем разделе). Затем значение  может быть интерполировано, как описано выше.
может быть интерполировано, как описано выше.
Эти методы имеют множество применений, например, метод конечных элементов (FEM).
Интегрирование по треугольнику или тетраэдру
Вычисление интеграла функции по области треугольника в декартовой системе координат может утомить. Обычно нужно разделить треугольник на две половины, и это приведет к большой неразберихе. Вместо этого часто проще выполнить замену переменных на любые две барицентрические координаты, например  . При такой замене переменных
. При такой замене переменных

где  - это область треугольника. Этот результат следует из того факта, что прямоугольник в барицентрических координатах соответствует четырехугольнику в декартовых координатах, а соотношение площадей соответствующих форм в соответствующих системах координат определяется как
- это область треугольника. Этот результат следует из того факта, что прямоугольник в барицентрических координатах соответствует четырехугольнику в декартовых координатах, а соотношение площадей соответствующих форм в соответствующих системах координат определяется как  . Аналогично, для интегрирования по тетраэдру, вместо того, чтобы разбивать интеграл на две или три отдельные части, можно было бы переключиться на трехмерные тетраэдрические координаты при замене переменных
. Аналогично, для интегрирования по тетраэдру, вместо того, чтобы разбивать интеграл на две или три отдельные части, можно было бы переключиться на трехмерные тетраэдрические координаты при замене переменных

где

- объем тетраэдра.
Примеры особых точек
Три вершины треугольника имеют барицентрические координаты 
Центроид имеет барицентрику 
центр описанной окружности треугольника ABC имеет барицентрические координаты


где a, b, c - длины ребер BC, CA, AB соответственно треугольника.
Ортоцентр имеет барицентрические координаты


Interter имеет барицентные координаты ric

Барицентрики excenters - это

девятиточечный центр имеет барицентрические координаты

![{\ displaystyle = [a ^ {2} (b ^ {2} + c ^ {2}) - (b ^ {2} -c ^ {2}) ^ { 2}]: [b ^ {2} (c ^ {2} + a ^ {2}) - (c ^ {2} -a ^ {2}) ^ {2}]: [c ^ {2} ( a ^ {2} + b ^ {2}) - (a ^ {2} -b ^ {2}) ^ {2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f089d53cef3483e79aa1e2c5214b4c1744867c70)
Барицентрические координаты на тетраэдрах
Барицентрические координаты можно легко расширить до трех измерений. Трехмерный симплекс представляет собой тетраэдр, многогранник, имеющий четыре треугольные грани и четыре вершины. Опять же, четыре барицентрических координатных решения так, что первая вершина  отображается в барицентрические координаты
отображается в барицентрические координаты  ,
,  и т. д.
и т. д.
Это снова линейное преобразование, и мы можем описать вышеупомянутые треугольники, чтобы найти барицентрические координаты  относительно тетраэдра:
относительно тетраэдра:

где  теперь является матрицей 3 × 3:
теперь является матрицей 3 × 3:

и  с поставкой декартовыми координатами:
с поставкой декартовыми координатами:

И снова проблема поиска барицентрической системы координат были сокращены до инвертирования матрицы 3 × 3. Трехмерные барицентрические координаты координаты для определения, находится ли точка внутри тетраэдрического размера, и для интерполяции функции в тетраэдрической сетке аналогично двухмерной процедуре. Тетраэдральные сетки часто используются в
анализе методом конечных элементов, поскольку использование барицентрических координат может значительно упростить трехмерную интерполяцию.
Обобщенные барицентрические координаты
Барицентрические координаты (a 1,..., a n), которые определены относительно конечного набора точек вместо симплекс называются обобщенными барицентрическими координатами. Для них уравнение

по-прежнему требуется для удержания, где x 1,..., x n - заданные точки. Если эти данные точки не образуют симплекс, обобщенные барицентрические координаты точки p не уникальны (с точностью до скалярного умножения). Что касается симплекса, точки с неотрицательными обобщенными координатами образуют выпуклую оболочку x 1,..., x n.
Таким образом, определение формально не меняется, но в то время как симплекс с n вершинами должен быть встроен в векторное пространство размерности не менее n-1, многогранник может быть встроен в векторное пространство более низкой размерности. Самый простой пример - четырехугольник на плоскости. Следовательно, даже нормализованные обобщенные барицентрические координаты (то есть координаты, в которых сумма коэффициентов равна 1), как правило, больше не определяются однозначно, в то время как это имеет место для нормализованных барицентрических координат относительно симплекса.
Более абстрактно, обобщенные барицентрические координаты выражают выпуклый многогранник с n вершинами, независимо от размерности, как изображение стандартного  -симплекс, имеющий n вершин - карта находится на:
-симплекс, имеющий n вершин - карта находится на:  Карта взаимно однозначна тогда и только тогда, когда многогранник является симплексом, и в этом случае карта является изоморфизмом; это соответствует точке, не имеющей уникальных обобщенных барицентрических координат, за исключением случая, когда P является симплексом.
Карта взаимно однозначна тогда и только тогда, когда многогранник является симплексом, и в этом случае карта является изоморфизмом; это соответствует точке, не имеющей уникальных обобщенных барицентрических координат, за исключением случая, когда P является симплексом.
Двойные к обобщенным барицентрическим координатам - это переменные запаса, которые измеряют, насколько точка удовлетворяет линейным ограничениям, и дает вложение  в f- orthant, где f - количество граней (двойственных вершинам). Эта карта взаимно однозначна (переменные резерва определяются однозначно), но не взаимно (не все комбинации могут быть реализованы).
в f- orthant, где f - количество граней (двойственных вершинам). Эта карта взаимно однозначна (переменные резерва определяются однозначно), но не взаимно (не все комбинации могут быть реализованы).
Использование стандартных  -simplex и f-orthant в качестве стандартных объектов, которые отображаются в многогранник или отображение многогранника в должно быть противопоставлено с использованием стандартного векторного пространства
-simplex и f-orthant в качестве стандартных объектов, которые отображаются в многогранник или отображение многогранника в должно быть противопоставлено с использованием стандартного векторного пространства  в качестве стандартного объекта для векторных пространств и стандартного аффинного гиперплоскость
в качестве стандартного объекта для векторных пространств и стандартного аффинного гиперплоскость  в качестве стандартного объекта для аффинных пространств, где в каждом случае выбирается линейный базис или аффинный базис обеспечивает изоморфизм, позволяя мыслить все векторные пространства и аффинные пространства в терминах этих стандартных пространств, а не отображать на или взаимно однозначное отображение (не каждый многогранник является симплексом). Кроме того, н-ортант - это стандартный объект, который отображается на конусы.
в качестве стандартного объекта для аффинных пространств, где в каждом случае выбирается линейный базис или аффинный базис обеспечивает изоморфизм, позволяя мыслить все векторные пространства и аффинные пространства в терминах этих стандартных пространств, а не отображать на или взаимно однозначное отображение (не каждый многогранник является симплексом). Кроме того, н-ортант - это стандартный объект, который отображается на конусы.
Приложения
Обобщенные барицентрические координаты имеют приложения в компьютерной графике и, более конкретно, в геометрическом моделировании. Часто трехмерную модель можно аппроксимировать многогранником, так что обобщенные барицентрические координаты по отношению к этому многограннику имеют геометрический смысл. Таким образом, обработка модели может быть упрощена за счет использования этих значимых координат. Барицентрические координаты также используются в геофизике
.
См. Также
Ссылки
- ^Август Фердинанд Мёбиус: Der barycentrische Calcul, Verlag von Johann Ambrosius Barth, Leipzig, 1827.
- ^Макс Кохер, Алоис Криг: Ebene Geometrie. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49328-0, S. 76.
- ^Хилле, Эйнар. "Теория аналитических функций, том I", второе издание, пятое издание. Chelsea Publishing Company, Нью-Йорк, 1982, ISBN 0-8284-0269-8, стр. 33, сноска 1
- ^Йозеф Хошек, Дитер Лассер: Grundlagen der geometriechen Datenverarbeitung. Teubner-Verlag, 1989, ISBN 3-519-02962-6, S. 243.
- ^Джеральд Фарин: кривые и поверхности для компьютерного геометрического проектирования. Academic Press, 1990, ISBN 0-12-249051-7, S. 20.
- ^Deaux, Roland. «Введение в геометрию комплексных чисел». Dover Publications, Inc., Mineola, 2008, ISBN 978-0-486-46629-3, стр. 61
- ^ Бергер, Марсель (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
- ^Дэнби, JMA «Основы небесной механики», второе издание, исправленное и дополненное, пятое издание. Willmann-Bell, Inc., Ричмонд, 2003, ISBN 0-943396-20-4, стр. 26, проблема 11
- ^ Скотт, Дж. А. «Некоторые примеры использование площадных координат в геометрии треугольника ", Mathematical Gazette 83, ноябрь 1999 г., 472–477.
- ^ Шиндлер, Макс; Чен, Эван (13 июля 2012 г.). "Барицентрические координаты в геометрии олимпиады" (PDF). Проверено 14 января 2016 года.
- ^Энциклопедия треугольников Кларка Кимберлинга «Энциклопедия треугольных центров». Архивировано с оригинального 19 апреля 2012 года. Проверено 2 июня 2012 г.
- ^Страница Вольфрама по барицентрическим координатам
- ^ Дасари Нага, Виджай Кришна, «О треугольнике Фейербаха», Forum Geometricorum 17 (2017), 289–300: стр. 289. http://forumgeom.fau.edu/FG2017volume17/FG201731.pdf
- ^ОНУФРИЕВ В.Г.; ДЕНИСИК, SA; ФЕРРОНСКИЙ В.И. БАРИЦЕНТРИЧЕСКИЕ МОДЕЛИ В ИЗОТОПНЫХ ИССЛЕДОВАНИЯХ ПРИРОДНЫХ ВОД. ЯДЕРНАЯ ГЕОФИЗИКА, 4, 111-117 (1990)
- Скотт, Дж. А. Некоторые примеры использования площадных координат в геометрии треугольника, Mathematical Gazette 83, ноябрь 1999 г., 472–477.
- Schindler, Max; Чен, Эван (13 июля 2012 г.). Барицентрические координаты в геометрии олимпиады (PDF). Проверено 14 января 2016 года.
- Энциклопедия треугольников Кларка Кимберлинга Энциклопедия треугольных центров. Архивировано 19 апреля 2012 года. Проверено 2 июня 2012 г.
- Брэдли, Кристофер Дж. (2007). Алгебра геометрии: декартовы, площадные и проективные координаты. Ванна: высокое восприятие. ISBN 978-1-906338-00-8.
- Coxeter, H.S.M. (1969). Введение в геометрию (2-е изд.). Джон Уайли и сыновья. Стр. 216 –221. ISBN 978-0-471-50458-0. Zbl 0181.48101.
- Барицентрическое исчисление в евклидовой и гиперболической геометрии: сравнительное введение, Абрахам Унгар, World Scientific, 2010
- Гиперболические барицентрические координаты, Абрахам А. Унгар, Австралийский журнал математического анализа и приложений, том 6, № 1, статья 18, стр. 1–35, 2009 г.
- Вайсштейн, Эрик У. «Координаты площади». MathWorld.
- Вайсштейн, Эрик У. «Барицентрические координаты». MathWorld.
- Вычисление барицентрических координат в однородных координатах, Вацлав Скала, Компьютеры и графика, Том 32, № 1, стр. 120–127, 2008 г. рычаг
Внешние ссылки
 3-симплексная система с барицентрическими подразделениями 1-граней (ребер) 2-гранями (треугольники) и 3-гранями (тело).
3-симплексная система с барицентрическими подразделениями 1-граней (ребер) 2-гранями (треугольники) и 3-гранями (тело). 























 Барицентрические координаты
Барицентрические координаты  в равностороннем треугольнике и в прямоугольном треугольнике.
в равностороннем треугольнике и в прямоугольном треугольнике. 





















![{\ displaystyle \ mathbf {h} = {\ frac {1} {(\ mathbf {e}, \ mathbf {f}, \ ma thbf {g})}} \ cdot \ left [(\ mathbf {h}, \ mathbf {f}, \ mathbf {g}) \ mathbf {e} + (\ mathbf {e}, \ mathbf {h}, \ mathbf {g}) \ mathbf {f} + (\ mathbf {e}, \ mathbf {f}, \ mathbf {h}) \ mathbf {g} \ right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b1318f42d7c5bac15a253331f26a3a18a519e45)















































































![{\ displaystyle d ^ {2} = \ left | PQ \ right | ^ {2} = - a ^ {2} yz-b ^ {2} zx-c ^ {2} xy = {\ frac {1} {2}} [x ^ {2} (b ^ {2} + c ^ {2} -a ^ {2}) + y ^ {2} (c ^ {2} + a ^ {2} -b ^ {2}) + z ^ {2} (a ^ {2} + b ^ {2} -c ^ {2})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc8615c8fe62884423e5e671a2b1a4cf5cd145ad)


 Два решения 8, 5 и 3 л заливка воды с использованием барицентрического графика. Желтая область обозначает комбинации, достижимые с кувшинами. Сплошные красные и пунктирные синие пути показывают текучие переходы. Когда вершина попадает в пунктирный треугольник, было измерено 4 л.
Два решения 8, 5 и 3 л заливка воды с использованием барицентрического графика. Желтая область обозначает комбинации, достижимые с кувшинами. Сплошные красные и пунктирные синие пути показывают текучие переходы. Когда вершина попадает в пунктирный треугольник, было измерено 4 л. 



 лежит внутри треугольника тогда и только тогда, когда
лежит внутри треугольника тогда и только тогда, когда  .
. лежит на краю или углу треугольника, если
лежит на краю или углу треугольника, если  и
и  .
. лежит вне треугольника.
лежит вне треугольника. Поверхность (верхняя часть), полученная в результате линейной интерполяции по заданной треугольной сетке (нижняя часть) в плоскости x, y. Поверхность аппроксимирует функцию z = f (x, y), учитывая только значения f в вершинах сетки.
Поверхность (верхняя часть), полученная в результате линейной интерполяции по заданной треугольной сетке (нижняя часть) в плоскости x, y. Поверхность аппроксимирует функцию z = f (x, y), учитывая только значения f в вершинах сетки. 


















 где
где  - объем тетраэдра.
- объем тетраэдра. 






![{\ displaystyle = [a ^ {2} (b ^ {2} + c ^ {2}) - (b ^ {2} -c ^ {2}) ^ { 2}]: [b ^ {2} (c ^ {2} + a ^ {2}) - (c ^ {2} -a ^ {2}) ^ {2}]: [c ^ {2} ( a ^ {2} + b ^ {2}) - (a ^ {2} -b ^ {2}) ^ {2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f089d53cef3483e79aa1e2c5214b4c1744867c70)








 И снова проблема поиска барицентрической системы координат были сокращены до инвертирования матрицы 3 × 3. Трехмерные барицентрические координаты координаты для определения, находится ли точка внутри тетраэдрического размера, и для интерполяции функции в тетраэдрической сетке аналогично двухмерной процедуре. Тетраэдральные сетки часто используются в анализе методом конечных элементов, поскольку использование барицентрических координат может значительно упростить трехмерную интерполяцию.
И снова проблема поиска барицентрической системы координат были сокращены до инвертирования матрицы 3 × 3. Трехмерные барицентрические координаты координаты для определения, находится ли точка внутри тетраэдрического размера, и для интерполяции функции в тетраэдрической сетке аналогично двухмерной процедуре. Тетраэдральные сетки часто используются в анализе методом конечных элементов, поскольку использование барицентрических координат может значительно упростить трехмерную интерполяцию. 





