Квадратура Гаусса

Сравнение двухточечной квадратуры Гаусса и трапеции. Синяя линия - это многочлен $y\; (x)\; =\; 7\; x\; 3\; -\; 8\; x\; 2\; -\; 3\; x\; +\; 3\; \{\backslash \; textstyle\; y\; (x)\; =\; 7x\; ^\; \{3\}\; -8x\; ^\; \{2\}\; -3x\; +\; 3\}.$, интеграл которого в [−1, 1] равенство ⁄ 3. Правило трапеции возвращает интеграл оранжевой пунктирной линии, равный $y\; (-\; 1)\; +\; y\; (1)\; =\; -\; 10\; \{\backslash \; textstyle\; y\; (-1)\; +\; y\; (1)\; =\; -10\}$. Двухточечное квадратурное правило Гаусса возвращает интеграл черной пунктирной кривой, равный $y\; (-\; 1\; 3)\; +\; y\; (1\; 3)\; =\; 2\; 3\; \{\backslash \; textstyle\; y\; \backslash \; left\; (-\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \}\; \backslash \; right)\; +\; y\; \backslash \; left\; (\{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{3\}\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}$. Такой результат является точным, поскольку зеленая область ту же площадь.

В исследуемом квадратурное правило является приближением интеграл функции , обычно выражаемый как взвешенная сумма значений функции в указанных точках в пределах области интегрирования. (См. численное интегрирование для получения дополнительной информации о квадратурных правил.) N-точечное квадратурное правило Гаусса, названное в честь Карла Фридриха Гаусса, является квадратурным правилом, построенным для получения точного результата для многочленов степени 2n - 1 или меньше подходящего путем выбора узлов x i и весов w i для i = 1,…, п. Современная формулировка с использованием ортогональных многочленов была улучшена Карлом Густавом Якоби 1826 г. Самая распространенная область интегрирования для такого правила берется как [−1, 1], поэтому правило сформулировано как

$\int \; -\; 1\; 1\; f\; (x)\; dx\; \approx \; \sum \; i\; =\; 1\; nwif\; (xi),\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; f\; (x\_\; \{i\}),\}$

который точен для многочленов степени 2n - 1 или меньше. Это точное правило известно как квадратурное правило Гаусса-Лежандра. Правило квадратуры будет точным приближением к интегралу выше, только если f (x) хорошо аппроксимируется полиномом степени 2n - 1 или меньше на [−1, 1].

Квадратурное правило Гаусса- Лежандра обычно не используется для интегрируемых функций с конечными точками сингулярностями. Вместо этого, если подынтегральное выражение может быть записано как

$f\; (x)\; =\; (1\; -\; x)\; \alpha \; (1\; +\; x)\; \beta \; g\; (x),\; \alpha ,\; \beta >-\; 1,\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; left\; (1-x\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \backslash \; left\; (1\; +\; x\; \backslash \; right)\; ^\; \{\backslash \; beta\}\; g\; (x),\; \backslash \; quad\; \backslash \; alpha,\; \backslash \; beta>-1,\}$

где g (x) хорошо аппроксимируется полиномом низкой степени, альтернативные узлы $xi\; \prime \; \{\backslash \; displaystyle\; x\_\; \{i\}\; \text{'}\}$и вес $wi\; \prime \; \{\backslash \; displaystyle\; w\_\; \{i\}\text{'}\}$обычно дает более точные квадратные правила. Они известны как квадратные правила Гаусса-Якоби, т. Е.

$\int \; -\; 1\; 1\; f\; (x)\; dx\; =\; \int \; -\; 1\; 1\; (1\; -\; Икс)\; \alpha \; (1\; +\; Икс)\; \beta \; g\; (Икс)\; dx\; \approx \; \sum \; я\; =\; 1\; nwi\; \prime \; g\; (xi\; \prime ).\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; f\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; \backslash \; left\; (1-x\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \backslash \; left\; (1\; +\; x\; \backslash \; right)\; ^\; \{\backslash \; beta\}\; g\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; \text{'}g\; \backslash \; left\; (x\_\; \{i\}\text{'}\; \backslash \; right).\}$

Общие включают веса $1\; 1\; -\; x\; 2\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1-x\; ^\; \{\; 2\}\}\}\}\}$(Чебышев - Гаусс ) и $1\; -\; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\}$. Также может потребоваться интегрирование по полубесконечному (квадратура Гаусса-Лагерра ) и бесконечным интервалам (квадратура Гаусса-Эрмита ).

Можно показать (см. Пресс и др. Или Стоер и Булирш), что квадратные узлы x i являются корнями полинома, принадлежащего классу ортогональных многочленов (класс, ортогональный относительно взвешенного скалярного произведения). Это определение для вычисления квадратурных узлов и весов Гаусса.

• 1 Квадратура Гаусса - Лежандра
• 2 Изменение интервала
• 3 Другие
  • 3.1 Основная форма теорема
    • 3.1.1 Общая формула для весов
    • 3.1.2 Доказательство того, что веса положительные
  • 3.2 Вычисление квадратурных правил Гаусса
    • 3.2.1 Отношение рекуррентности
    • 3.2.2 Алгоритм Голуба-Велша
  • 3.3 Оценки ошибок
  • 3.4 Правила Гаусса - Кронрода
  • 3.5 Правила Гаусса - Лобатто
• 4 Ссылки
• 5 Внешние ссылки

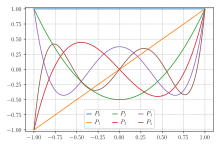
Графы полиномов Лежандра (до n = 5)

Для простейшей задачи интегрирования, выше, т. Е. F (x) хорошо аппроксимируется многочленами от $[-\; 1,\; 1]\; \{\backslash \; displaystyle\; [-1,1]\}$, соответствующие ортогональные многочлены - это многочлены Лежандра, обозначается P n (х). С n-м полиномом, нормализованным для получения P n (1) = 1, i-й узел Гаусса, x i, является i-м корнем из P n, данные веса по формуле (Abramowitz Stegun 1972, p. 887) harv error: no target: CITEREFAbramowitzStegun1972 (help )

$wi\; =\; 2\; (1\; -\; xi\; 2)\; [P\; n\; \text{'}(xi)]\; 2.\; \{\backslash \; Displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; left\; (1-x\_\; \{i\}\; ^\; \{2\}\; \backslash \; right)\; \backslash \; left\; [P\text{'}\; \_\; \{n\}\; (x\_\; \{i\})\; \backslash \; right]\; ^\; \{2\}\}\}.\}$

Некоторые квадратурные правила младшего порядка сведены в таблицу (для интервала [-1, 1], другие интервалы см. в разделе ниже).

Количество точек, n	точек, x i		Вес, w i
1	0		2
2	$\pm \; 1\; 3\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{3\}\}\}\}$	± 0, 57735…	1
3	0		$8\; 9\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{8\}\; \{9\}\}\}$	0,888889…
	$\pm \; 3\; 5\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{3\}\; \{5\}\; \}\}\}\}$	± 0,774597…	$5\; 9\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{5\}\; \{9\}\}\}$	0,555556…
4	$\pm \; 3\; 7\; -\; 2\; 7\; 6\; 5\; \{\; \backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{3\}\; \{7\}\}\; -\; \{\backslash \; frac\; \{2\}\; \{7\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{6\}\; \{5\}\; \}\}\}\}\}$	± 0,339981…	$18\; +\; 30\; 36\; \{\backslash \; displaystyl\; е\; \{\backslash \; frac\; \{18\; +\; \{\backslash \; sqrt\; \{30\}\}\}\; \{36\}\}\}$	0,652145…
	$\pm \; 3\; 7\; +\; 2\; 7\; 6\; 5\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{3\}\; \{7\}\}\; +\; \{\backslash \; frac\; \{2\}\; \{7\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{6\}\; \{5\}\}\}\}\}\}$	± 0,861136…	$18–30\; 36\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{18\; -\; \{\backslash \; sqrt\; \{30\}\}\}\; \{36\}\}\}$	0, 347855…
5	0		$128\; 225\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{128\}\; \{225\}\}\}$	0,568889…
	$\pm \; 1\; 3\; 5\; -\; 2\; 10\; 7\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; \{5-2\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{10\}\; \{7\}\}\}\}\}\}$	± 0,538469…	$322\; +\; 13\; 70\; 900\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{322\; +\; 13\; \{\backslash \; sqrt\; \{70\}\}\}\; \{900\}\}\}$	0,478629…
	$\pm \; 1\; 3\; 5\; +\; 2\; 10\; 7\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \{\backslash \; sqrt\; \{5\; +\; 2\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{10\}\; \{7\}\}\}\}\}\}$	± 0,90618…	$322–13\; 70\; 900\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{322-13\; \{\backslash \; sqrt\; \{70\}\}\}\; \{900\}\}\}$	0,236927…

Интеграл по [a, b] необходимо преобразовать в интеграл по [−1, 1] перед Применение квадратурного правила Гаусса. Это изменение интервала может быть выполнено следующим образом:

$\int \; a\; b\; f\; (x)\; d\; x\; =\; b\; -\; a\; 2\; \int \; -\; 1\; 1\; f\; (b\; -\; a\; 2\; \xi \; +\; a\; +\; b\; 2)\; d\; \xi .\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; =\; \{\backslash \; frac\; \{ba\}\; \{2\}\}\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; f\; \backslash \; left\; (\{\backslash \; frac\; \{\; ba\}\; \{2\}\}\; \backslash \; xi\; +\; \{\backslash \; frac\; \{a\; +\; b\}\; \{2\}\}\; \backslash \; right)\; \backslash ,\; d\; \backslash \; xi.\}$

Применение $n\; \{\backslash \; displaystyle\; n\}$точечная квадратура Гаусса $(\xi ,\; w)\; \{\backslash \; displaystyle\; (\backslash \; xi,\; w)\}$затем дает следующее приближение:

$\int \; abf\; (x)\; dx\; \approx \; b\; -\; a\; 2\; \sum \; i\; =\; 1\; nwif\; (b\; -\; a\; 2\; \xi \; i\; +\; a\; +\; b\; 2).\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; f\; (x)\; \backslash ,\; dx\; \backslash \; приблизительно\; \{\backslash \; frac\; \{ba\}\; \{2\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; f\; \backslash \; left\; (\{\backslash \; frac\; \{ba\}\; \{2\}\}\; \backslash \; xi\; \_\; \{i\}\; +\; \{\backslash \; frac\; \{a\; +\; b\}\; \{2\}\}\; \backslash \; right).\}$

Проблема интеграции можно выразить несколько более общим образом, введя положительную весовую функцию ω в подынтегральную функцию и допустив интервал, отличный от [-1, 1]. То есть задача состоит в том, чтобы вычислить

$\int \; ab\; \omega \; (x)\; f\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash ,\; f\; (x)\; \backslash ,\; dx\; \}$

для некоторых вариантов a, b и ω. При a = −1, b = 1 и ω (x) = 1 задача такая же, как рассмотренная выше. Другие варианты приводят к другим правилам интеграции. Некоторые из них представлены в таблице ниже. Номера уравнений приведены для Абрамовица и Стегуна (AS).

Интервал	ω (x)	Ортогональные многочлены	AS	Для получения дополнительной информации см.…
[−1, 1]	1	Многочлены Лежандра	25.4.29	§ Квадратура Гаусса - Лежандра
(−1, 1)	$(1\; -\; x)\; \alpha \; (1\; +\; x)\; \beta ,\; \alpha ,\; \beta >-\; 1\; \{\backslash \; displaystyle\; \backslash \; left\; (1-x\; \backslash \; right)\; ^\; \{\backslash \; alpha\}\; \backslash \; left\; (1\; +\; x\; \backslash \; right)\; ^\; \{\backslash \; beta\},\; \backslash \; quad\; \backslash \; alpha,\; \backslash \; beta>-1\}$	Полином Якоби	25.4.33 (β = 0)	Квадратура Гаусса - Якоби
(−1, 1)	$1\; 1\; -\; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; -\; x\; ^\; \{2\}\}\}\}\}$	Многочлены Чебышева (первый вид)	25.4.38	Квадратура Чебышева - Гаусса
[−1, 1]	$1\; -\; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{1-x\; ^\; \{2\}\}\}\}$	Многочлены Чебышева (второй вид)	25.4.40	Квадратура Чебышева - Гаусса
[ 0, ∞)	$е\; -\; x\; \{\backslash \; displaystyle\; e\; ^\; \{-\; x\}\; \backslash ,\}$	Многочлены Лагерра	25.4.45	Квадратура Гаусса - Лагерра
[0, ∞)	$x\; \alpha \; e\; -\; x,\; \alpha >-\; 1\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; alpha\}\; e\; ^\; \{-\; x\},\; \backslash \; quad\; \backslash \; alpha>-1\}$	Generalized	Generalized 294>Многочлены Лагерра		Квадратура Гаусса - Лагерра
<2∞28, ∞>{\ displaystyle e ^ {- x ^ {2}}}	Многочлены Эрмита	25,4.46	квадратура Гаусса - Эрмита

Основная теорема

Пусть p n - нетривиальный многочлен степени n такой, что

$\int \; ab\; \omega \; (x)\; xkpn\; (x)\; dx\; =\; 0,\; для\; всех\; k\; =\; 0,\; 1,\dots ,\; n\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\; a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash ,\; x\; ^\; \{k\}\; p\_\; \{n\}\; (x)\; \backslash ,\; dx\; =\; 0,\; \backslash \; quad\; \{\backslash \; text\; \{для\; всех\}\}\; k\; =\; 0,1,\; \backslash \; ldots,\; n-1.\}$

Если мы выберем n узлов x i как нулей p n, то существует n весов w i, которые делают вычисленный квадратурной интеграл Г аусса точным для всех многочленов h (x) степени 2n - 1 или меньше. Кроме того, все эти узлы x i будут лежать в открытом интервале (a, b) (Stoer Bulirsch 2002, стр. 172–175).

Многочлен p n называется ортогональным многочленом степени n, ассоциированным с весовой функцией ω (x). Он уникален с точностью до постоянного нормирующего коэффициента. Идея, лежащая в основе доказательства, заключается в том, что из достаточно низкой степени h (x) можно разделить на $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$, чтобы получить частное q (x) степени строго ниже n, и остаток r (x) еще более низкой степени, так что оба будут ортогональны $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$, определяющим свойством $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$. Таким образом,

$\int \; a\; b\; \omega \; (x)\; h\; (x)\; d\; x\; =\; \int \; a\; b\; \omega \; (x)\; r\; (x)\; d\; x.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash ,\; h\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash ,\; r\; (x)\; \backslash ,\; dx.\}$

Из-за выбора узлов x i соответствующее соотношение

$\sum \; i\; =\; 1\; nwih\; (xi)\; =\; \sum \; i\; =\; 1\; nwir\; (xi)\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; h\; (x\_\; \{i\})\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; r\; (x\_\; \{i\})\}$

удерживается также. Точность вычисленного интеграла для $h\; (x)\; \{\backslash \; displaystyle\; h\; (x)\}$затем следует из системы точности для многочленов степени только n или меньше (как и $r\; (x)\; \{\backslash \; Displaystyle\; г\; (х)\}$).

Общая формула для весов

Веса могут быть выражены как

$wi\; =\; anan\; -\; 1\; \int \; ab\; \omega \; (x)\; pn\; -\; 1\; (x)\; 2\; dxpn\; \prime \; (xi)\; pn\; -\; 1\; (xi)\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{a\_\; \{n\}\}\; \{a\_\; \{n-1\}\}\}\; \{\backslash \; frac\; \{\backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; p\_\; \{\; n-1\}\; \backslash \; left\; (x\; \backslash \; right)\; ^\; \{2\}\; dx\}\; \{p\; \text{'}\_\; \{n\}\; (x\_\; \{i\})\; p\_\; \{n-1\}\; (x\_\; \{i\})\}\}\}$

(1)

где $ak\; \{\backslash \; displaystyle\; a\_\; \{k\}\}$- коэффициент $xk\; \{\backslash \; displaystyle\; x\; ^\; \{k\}\}$в $пк\; (х)\; \{\backslash \; displaystyle\; p\_\; \{k\}\; (x)\}$. Чтобы доказать это, обратите внимание, что с помощью интерполяции Лагранжа можно выразить r (x) через $r\; (xi)\; \{\backslash \; displaystyle\; r\; (x\_\; \{i\})\}$как

$р\; (Икс)\; знак\; равно\; \sum \; я\; знак\; равно\; 1\; NR\; (XI)\; \prod \; 1\; \le \; J\; \le \; NJ\; \ne \; ix\; -\; xjxi\; -\; xj\; \{\backslash \; Displaystyle\; г\; (х)\; =\; \backslash \; сумма\; \_\; \{я\; =\; 1\}\; ^\; \{п\}\; г\; (x\_\; \{i\})\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \{\backslash \; frac\; \{x-x\_\; \{j\}\}\; \{x\_\; \{i\; \}\; -\; x\_\; \{j\}\}\}\}$

потому что что r (x) имеет степень меньше, таким образом, фиксируется значениями, которые оно достигает в различных точках. Умножая обе части на ω (x) и объединяясь от a до b, получаем

$\int \; ab\; \omega \; (x)\; r\; (x)\; dx\; =\; \sum \; i\; =\; 1\; nr\; (xi)\; \int \; ab\; \omega \; (x)\; \prod \; 1\; \le \; j\; \le \; nj\; \ne \; ix\; -\; xjxi\; -\; xjdx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; r\; (x)\; dx\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; r\; (x\_\; \{i\})\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \{\backslash \; frac\; \{x-x\_\; \{j\}\}\; \{x\_\; \{i\}\; -x\_\; \{j\}\}\}\; dx\}$

Таким образом, вес w i задаются как

$wi\; =\; \int \; ab\; \omega \; (x)\; \prod \; 1\; \le \; j\; \le \; nj\; \ne \; ix\; -\; xjxi\; -\; xjdx\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \{\backslash \; frac\; \{x-x\_\; \{j\}\}\; \{x\_\; \{i\}\; -x\_\; \{j\}\}\}\; dx\}$

Это интегральное выражение для $wi\; \{\backslash \; displaystyle\; w\_\; \{\; i\}\}$может быть выражено через ортогональные многочлены $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$и $pn\; -\; 1\; (x)\; \{\; \backslash \; displaystyle\; p\_\; \{n-1\}\; (x)\}$следующим образом.

Мы можем написать

$\prod \; 1\; \le \; j\; \le \; nj\; \ne \; i\; (x\; -\; xj)\; =\; \prod \; 1\; \le \; j\; \le \; n\; (x\; -\; xj)\; x\; -\; xi\; =\; pn\; (x)\; an\; (x\; -\; xi)\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \backslash \; left\; (x-x\_\; \{j\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; prod\; \_\; \{1\; \backslash \; leq\; j\; \backslash \; leq\; n\}\; \backslash \; left\; (x-x\_\; \{j\}\; \backslash \; right)\}\; \{x-x\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{a\_\; \{n\; \}\; \backslash \; left\; (x-x\_\; \{i\}\; \backslash \; right)\}\}\}$

где $an\; \{\backslash \; displaystyle\; a\_\; \{n\}\}$- коэффициент при $xn\; \{\backslash \; displaystyle\; x\; ^\; \{n\}\}$в $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$. Если взять предел x равным $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$, получаем, используя правило Л'Опиталя

$\prod \; 1\; \le \; j\; \le \; nj\; \ne \; i\; (xi\; -\; xj)\; =\; pn\; \prime \; (xi)\; an\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \backslash \; left\; (x\_\; \{i\}\; -x\_\; \{j\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{p\; \text{'}\_\; \{n\}\; (x\_\; \{i\})\}\; \{a\_\; \{n\}\}\}\}$

Таким образом, мы можем записать интегральное выражение для весов как

$wi\; =\; 1\; pn\; \prime \; (xi)\; \int \; ab\; \omega \; (x)\; pn\; (x)\; x\; -\; xidx\; \{\backslash \; displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{1\}\; \{p\; \text{'}\_\; \{n\}\; (x\_\; \{i\})\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\}$

(2)

В подынтегральном выражении записав

$1\; x\; -\; xi\; =\; 1\; -\; (xxi)\; kx\; -\; xi\; +\; (xxi)\; k\; 1\; x\; -\; xi\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{x-x\_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{1-\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{x\_\; \{i\}\}\}\; \backslash \; right)\; ^\; \{k\}\}\; \{x-x\_\; \{i\}\}\}\; +\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{x\_\; \{i\}\}\}\; \backslash \; right)\; ^\; \{k\}\; \{\backslash \; frac\; \{1\}\; \{x-x\_\; \{i\}\}\}\}$

дает

$ab\; \omega \; (x)\; xkpn\; (x)\; x\; -\; xidx\; =\; xik\; \int \; ab\; \omega \; (x)\; pn\; (\; х)\; х\; -\; xidx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{x\; ^\; \{k\}\; p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\; =\; x\_\; \{i\}\; ^\; \{k\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; гидроразрыв\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\}$

при условии $k\; \le \; n\; \{\backslash \; displaystyle\; k\; \backslash \; leq\; n\}$, потому что

$1\; -\; (xxi)\; kx\; -\; xi\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1-\; \backslash \; left\; (\{\backslash \; frac\; \{x\}\; \{x\_\; \{i\}\}\}\}\; \backslash \; right)\; ^\; \{k\}\}\; \{x-x\_\; \{i\}\; \}\}\}$

- многочлен степени k - 1, который ортогонален $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$. Итак, если q (x) - многочлен не более n-й степени, то

$\int \; ab\; \omega \; (x)\; pn\; (x)\; x\; -\; xidx\; =\; 1\; q\; (xi)\; \int \; ab\; \omega \; (x)\; q\; (x)\; pn\; (x)\; x\; -\; xidx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\; =\; \{\backslash \; frac\; \{1\}\; \{q\; (x\_\; \{i\})\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{q\; (x)\; p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\; \}\}\}\; dx\}$

Мы можем вычислить интеграл в правой части для $q\; (x)\; =\; pn\; -\; 1\; (x)\; \{\backslash \; displaystyle\; q\; (x)\; =\; p\_\; \{n-1\}\; (x)\}$следующим образом. <Времена $pn\; (x)\; x\; -\; xi\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\}$- многочлен степени n - 1, мы имеем

$pn\; (x)\; x\; -\; xi\; =\; тревога\; -\; 1\; +\; s\; (x)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; =\; a\_\; \{n\}\; x\; ^\; \{n-1\}\; +\; s\; (x)\}$

где s (x) - многочлен степени $n\; -\; 2\; \{\backslash \; displaystyle\; n-2\}$. S (x) ортогонален $pn\; -\; 1\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n-1\}\; (x)\}$, мы имеем

$\int \; ab\; \omega \; (x)\; pn\; (x)\; Икс\; -\; xidx\; =\; anpn\; -\; 1\; (xi)\; \int \; ab\; \omega \; (x)\; pn\; -\; 1\; (x)\; xn\; -\; 1\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{p\_\; \{\; n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\; =\; \{\backslash \; frac\; \{a\_\; \{n\}\}\; \{p\_\; \{n-1\}\; (x\_\; \{i\})\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\; \}\; \backslash \; omega\; (x)\; p\_\; \{n-1\}\; (x)\; x\; ^\; \{n-1\}\; dx\}$

Тогда мы можем написать

$xn\; -\; 1\; =\; (xn\; -\; 1\; -\; pn\; -\; 1\; (x)\; an\; -\; 1)\; +\; pn\; -\; 1\; (x)\; an\; -\; 1\; \{\backslash \; displaystyle\; x\; ^\; \{n-1\}\; =\; \backslash \; left\; (x\; ^\; \{n-1\}\; -\; \{\backslash \; frac\; \{p\_\; \{n-1\}\; (x)\})\; \{a\_\; \{n-1\}\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{p\_\; \{n-1\}\; (x)\}\; \{a\_\; \{n-1\}\}\}\}$

Член в скобках представляет собой многочлен степени $n\; -\; 2\; \{\backslash \; displaystyle\; n-2\}$, поэтому ортогонален $pn\; -\; 1\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n-1\}\; (x)\}$. Таким образом, интеграл может быть записан как

$\int \; ab\; \omega \; (x)\; pn\; (x)\; x\; -\; xidx\; =\; anan\; -\; 1\; pn\; -\; 1\; (xi)\; \int \; ab\; \omega \; (x)\; pn\; -\; 1\; (x)\; 2\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \{\backslash \; frac\; \{p\_\; \{n\}\; (x)\}\; \{x-x\_\; \{i\}\}\}\; dx\; =\; \{\backslash \; frac\; \{a\_\; \{n\}\}\; \{a\_\; \{n-1\}\; p\_\; \{n-1\}\; (x\_\; \{i\})\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; p\_\; \{n-1\}\; (x)\; ^\; \{2\}\; dx\}$

Согласно уравнению (2) веса получаются путем деления полученного значения на $pn\; \prime \; (xi)\; \{\backslash \; displaystyle\; p\; \text{'}\_\; \{n\}\; (x\_\; \{i\})\}$и что дает выражение в уравнении (1).

$wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$также может быть выражено через ортогональные многочлены $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$и теперь $pn\; +\; 1\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\; +\; 1\}\; (x)\}$. В трехчленном рекуррентном предложении $pn\; +\; 1\; (xi)\; =\; (a)\; pn\; (xi)\; +\; (b)\; pn\; -\; 1\; (xi)\; \{\backslash \; displaystyle\; p\_\; \{n\; +\; 1\}\; (x\_\; \{i\})\; =\; (a)\; p\_\; \{n\}\; (x\_\; \{i\})\; +\; (b)\; p\_\; \{n-1\}\; (x\_\; \{i\})\}$термин с $pn\; (xi)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (\; x\_\; \{i\})\}$исчезает, поэтому $pn\; -\; 1\; (xi)\; \{\backslash \; displaystyle\; p\_\; \{n-1\}\; (x\_\; \{i\})\}$в уравнении. (1) можно заменить на $1\; bpn\; +\; 1\; (xi)\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{1\}\; \{b\}\}\; p\_\; \{n\; +\; 1\}\; \backslash \; left\; (x\_\; \{i\}\; \backslash \; right)\}$.

Доказательство положительности весов

Рассмотрим следующий многочлен степени $2\; n\; -\; 2\; \{\backslash \; displaystyle\; 2n-2\}$

$f\; (x)\; =\; \prod \; 1\; \le \; j\; \le \; nj\; \ne \; i\; (x\; -\; xj)\; 2\; (xi\; -\; xj)\; 2\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; prod\; \_\; \{\backslash \; begin\; \{smallmatrix\}\; 1\; \backslash \; leq\; j\; \backslash \; leq\; n\; \backslash \backslash \; j\; \backslash \; neq\; i\; \backslash \; end\; \{smallmatrix\}\}\; \{\backslash \; frac\; \{\backslash \; left\; (x-x\_\; \{j\}\; \backslash \; right)\; ^\; \{2\}\}\; \{\backslash \; left\; (x\_\; \{i\}\; -x\_\; \{j\}\; \backslash \; right)\; ^\; \{2\}\}\}\}$

где, как и выше, x j - корни многочлена $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$. Очевидно, $f\; (x\; j)\; =\; \delta \; i\; j\; \{\backslash \; displaystyle\; f\; (x\_\; \{j\})\; =\; \backslash \; delta\; \_\; \{ij\}\}$. Степень степени $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$меньше $2\; n\; -\; 1\; \{\backslash \; displaystyle\; 2n-1\}$, Применяется квадратурная формула Гаусса, включающая вес и узлы, полученный из $pn\; (x)\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\}$. $f\; (xj)\; =\; 0\; \{\backslash \; displaystyle\; f\; (x\_\; \{j\})\; =\; 0\}$для j, не равного i, мы имеем

$\int \; ab\; \omega \; (x)\; f\; (x)\; dx\; =\; \sum \; j\; =\; 1\; N\; wjf\; (xj)\; =\; \sum \; j\; =\; 1\; N\; \delta \; ijwj\; =\; wi>0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; f\; (x)\; dx\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{N\}\; w\_\; \{j\}\; f\; (x\_\; \{j\})\; =\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{N\}\; \backslash \; delta\; \_\; \{ij\}\; w\_\; \{j\}\; =\; w\_\; \{i\}>0.\}$

оба $\omega \; (x)\; \{\backslash \; displaystyle\; \backslash \; omega\; (x)\}$и $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$- неотрицательные функции, отсюда следует, что $wi>0\; \{\backslash \; displaystyle\; w\_\; \{i\}>0\}$.

Вычисление квадратных правил Гаусса

Существует множество алгоритмов для вычислительных узлов x i и весов w i квадратных правил Гаусса. Наиболеепопулярны алгоритм Голуба-Велша, требующие решения O (n) операций, метод Ньютона для $pn\; (x)\; =\; 0\; \{\backslash \; displaystyle\; p\_\; \{n\}\; (x)\; =\; 0\}$с использованием трехчленное повторение для оценки, требующейся O (n) операций, и асимптотические формулы для больших n, требующихся O (n) операций.

Отношение повторяемости

Ортогональные многочлены $pr\; \{\backslash \; displaystyle\; p\_\; \{r\}\}$с $(pr,\; ps)\; =\; 0\; \{\backslash \; displaystyle\; (p\_\; \{r\},\; p\_\; \{s\})\; =\; 0\}$для $r\; \ne \; s\; \{\backslash \; displaystyle\; r\; \backslash \; neq\; s\}$для скалярного произведения $(,)\; \{\backslash \; displaystyle\; (\backslash ,,\; \backslash ,)\}$, степень $(pr)\; =\; r\; \{\backslash \; displaystyle\; (p\_\; \{r\})\; =\; r\}$и ведущий коэффициент один (т. е. monic ортогональные многочлены) удовлетворяют рекуррентному действию

$pr\; +\; 1\; (x)\; =\; (x\; -\; ar,\; r)\; pr\; (x)\; -\; ar,\; r\; -\; 1\; pr\; -\; 1\; (x)\; \cdots \; -\; ар,\; 0\; п\; 0\; (Икс)\; \{\backslash \; Displaystyle\; р\_\; \{г\; +\; 1\}\; (х)\; =\; (х-а\_\; \{г,\; г\})\; р\_\; \{г\}\; (х)\; -а\_\; \{г,\; г-1\}\; р\_\; \{г\; -\; 1\}\; (x)\; \backslash \; cdots\; -a\_\; \{r,\; 0\}\; p\_\; \{0\}\; (x)\}$

и определенное скалярное произведение

$(f\; (x),\; g\; (x))\; =\; \int \; ab\; \omega \; (x)\; е\; (Икс)\; г\; (Икс)\; dx\; \{\backslash \; Displaystyle\; (е\; (х),\; г\; (х))\; =\; \backslash \; int\; \_\; \{а\}\; ^\; \{b\}\; \backslash \; омега\; (х)\; е\; (х)\; г\; (х)\; dx\}$

для $r\; =\; 0,\; 1,\dots ,\; n\; -\; 1\; \{\backslash \; displaystyle\; r\; =\; 0,1,\; \backslash \; ldots,\; n-1\}$, где n - максимальная степень, которую можно принять быть бе ско нечностью, и где $ar,\; s\; =\; (xpr,\; ps)\; (ps,\; ps)\; \{\backslash \; textstyle\; a\_\; \{r,\; s\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; (xp\_\; \{r\},\; p\_\; \{s\}\; \backslash \; right)\; \}\; \{\backslash \; left\; (p\_\; \{s\},\; p\_\; \{s\}\; \backslash \; right)\}\}\}$. Прежде всего, многочлены, определяемые рекуррентным введением, начинающимся с $p\; 0\; (x)\; =\; 1\; \{\backslash \; displaystyle\; p\_\; \{0\}\; (x)\; =\; 1\}$, имеют старший коэффициент один и правильную степень. Учитывая начальную точку $p\; 0\; \{\backslash \; displaystyle\; p\_\; \{0\}\}$, ортогональность $pr\; \{\backslash \; displaystyle\; p\_\; \{r\}\}$может быть испытанием как индукция. Для $r\; =\; s\; =\; 0\; \{\backslash \; displaystyle\; r\; =\; s\; =\; 0\}$один имеет

$(p\; 1,\; p\; 0)\; =\; (x\; -\; a\; 0,\; 0)\; (p\; 0,\; p\; 0)\; знак\; равно\; (xp\; 0,\; p\; 0)\; -\; a\; 0,\; 0\; (p\; 0,\; p\; 0)\; =\; (xp\; 0,\; p\; 0)\; -\; (xp\; 0,\; p\; 0)\; =\; 0.\; \{\backslash \; displaystyle\; (p\_\; \{1\},\; p\_\; \{0\})\; =\; (x-a\_\; \{0,0\})\; (p\_\; \{0\},\; p\_\; \{0\})\; =\; (xp\_\; \{0\},\; p\_\; \{0\})\; -\; a\_\; \{0,0\}\; (p\_\; \{\; 0\},\; p\_\; \{0\})\; =\; (xp\_\; \{0\},\; p\_\; \{0\})\; -\; (xp\_\; \{0\},\; p\_\; \{0\})\; =\; 0.\}$

Теперь, если $p\; 0,\; p\; 1,\dots ,\; Пр\; \{\backslash \; displaystyle\; p\_\; \{0\},\; p\_\; \{1\},\; \backslash \; ldots,\; p\_\; \{r\}\}$ортогональны, тогда также $pr\; +\; 1\; \{\backslash \; displaystyle\; p\_\; \{r\; +\; 1\}\; \}$, потому что в

$(pr\; +\; 1,\; ps)\; =\; (xpr,\; ps)\; -\; ar,\; r\; (pr,\; ps)\; -\; ar,\; r\; -\; 1\; (pr\; -\; 1,\; ps)\; \cdots \; -\; ar,\; 0\; (p\; 0,\; ps)\; \{\backslash \; displaystyle\; (p\_\; \{r\; +\; 1\},\; p\_\; \{s\})\; =\; (xp\_\; \{r\},\; p\_\; \{s\})\; -\; a\_\; \{r,\; r\}\; (p\_\; \{r\},\; p\_\; \{s\})\; -\; a\_\; \{r,\; r-1\}\; (p\_\; \{r-1\},\; p\_\; \{s\})\; \backslash \; cdots\; -a\_\; \{r,\; 0\}\; (p\_\; \{0\},\; p\_\; \{s\})\}$

все скалярные исчезают, кроме первого и того, где $ps\; \{\backslash \; displaystyle\; p\_\; \{s\}\}$соответствует и тому же одному ортогональному многочлену. Следовательно,

$(pr\; +\; 1,\; ps)\; =\; (xpr,\; ps)\; -\; ar,\; s\; (ps,\; ps)\; =\; (xpr,\; ps)\; -\; (xpr,\; ps)\; =\; 0.\; \{\backslash \; displaystyle\; (p\_\; \{r\; +\; 1\},\; p\_\; \{s\})\; =\; (xp\_\; \{r\},\; p\_\; \{s\})\; -\; a\_\; \{r,\; s\}\; (p\_\; \{s\},\; p\_\; \{s\})\; =\; (xp\_\; \{r\},\; p\_\; \{s\})\; -\; (xp\_\; \{r\},\; p\_\; \{s\})\; =\; 0.\}$

Однако, если скалярное произведение удовлетворяет $(xf,\; g)\; =\; (f,\; xg)\; \{\backslash \; displaystyle\; (xf,\; g)\; =\; (f,\; xg)\}$(что имеет место для квадратур Гаусса) рекуррентное соотношение сводится к трехчленному рекуррентному использованию: для - это многочленность степени, меньшей или равной r - 1. С другой стороны, $pr\; \{\backslash \; displaystyle\; p\_\; \{r\}\}$ортогонален любому многочлену степени меньше или равной r - 1. Следовательно, $(xpr,\; ps)\; =\; (pr,\; xps)\; =\; 0\; \{\backslash \; displaystyle\; (xp\_\; \{r\; \},\; p\_\; \{s\})\; =\; (p\_\; \{r\},\; xp\_\; \{s\})\; =\; 0\}$и $ar,\; s\; =\; 0\; \{\backslash \; displaystyle\; a\_\; \{r,\; s\}\; =\; 0\}$для s < r − 1. The recurrence relation then simplifies to

$пр\; +\; 1\; (x)\; =\; (x\; -\; ar,\; r)\; pr\; (x)\; -\; ar,\; r\; -\; 1\; пр\; -\; 1\; (Икс)\; \{\backslash \; Displaystyle\; р\_\; \{г\; +\; 1\}\; (\; х)\; =\; (х-а\_\; \{г,\; г\})\; р\_\; \{г\}\; (х)\; -а\_\; \{г,\; г-1\}\; р\_\; \{г-\; 1\}\; (x)\}$

или

$пр\; +\; 1\; (\; Икс)\; =\; (Икс\; -\; ar)\; пр\; (х)\; -\; brpr\; -\; 1\; (х)\; \{\backslash \; Displaystyle\; р\_\; \{г\; +\; 1\}\; (х)\; =\; (х-а\_\; \{г\})\; р\_\; \{г\}\; (х)\; -b\_\; \{г\}\; р\_\; \{r-1\}\; (x)\}$

(согласно условию $p\; -\; 1\; (x)\; \equiv \; 0\; \{\backslash \; displaystyle\; p\; \_\; \{-\; 1\}\; (x)\; \backslash \; Equiv\; 0\}$), где

$ar:\; =\; (xpr,\; pr)\; (pr,\; pr),\; br:\; =\; (xpr,\; pr\; -\; 1)\; (pr\; -\; 1,\; pr\; -\; 1)\; =\; (pr,\; pr)\; (pr\; -\; 1,\; pr\; -\; 1))\; \{\backslash \; displaystyle\; a\_\; \{r\}:\; =\; \{\backslash \; frac\; \{(xp\_\; \{r\},\; p\_\; \{r\})\}\; \{(p\_\; \{r\},\; p\_\; \{r\})\}\},\; \backslash \; qquad\; b\_\; \{r\}\; :\; =\; \{\backslash \; frac\; \{(xp\_\; \{r\},\; p\_\; \{r-1\})\}\; \{(p\_\; \{r-1\},\; p\_\; \{r-1\})\}\}\; =\; \{\backslash \; frac\; \{(p\_\; \{r\},\; p\_\; \{r\}))\}\; \{(p\_\; \{r-1\},\; p\_\; \{r-1\})\}\}\}$

(послний из-за $(xpr,\; pr\; -\; 1)\; =\; (pr,\; xpr\; -\; 1)\; =\; (пр,\; пр)\; \{\backslash \; displaystyle\; (xp\_\; \{r\},\; p\_\; \{r-1\})\; =\; (p\_\; \{r\},\; xp\_\; \{r-1\})\; =\; (p\_\; \{r\},\; p\_\; \{r\})\; \}$, поскольку $xpr\; -\; 1\; \{\backslash \; displaystyle\; xp\_\; \{r-1\}\}$отличается от $pr\; \{\backslash \; displaystyle\; p\_\; \{r\}\}$на градус меньше чем r).

Алгоритм Голуба-Велша

Трехчленное рекуррентное соотношение может быть записано в матричной форме $JP\; ~\; =\; x\; P\; ~\; -\; pn\; (x)\; \times \; en\; \{\backslash \; displaystyle\; J\; \{\backslash \; tilde\; \{P\; \}\}\; =\; x\; \{\backslash \; tilde\; \{P\}\}\; -\; p\_\; \{n\}\; (x)\; \backslash \; times\; \backslash \; mathbf\; \{e\}\; \_\; \{n\}\}$где $P\; ~\; =\; [p\; 0\; (x)\; p\; 1\; (x)\dots \; pn\; -\; 1\; (x)]\; T\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{P\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; p\_\; \{0\}\; (x)\; p\_\; \{1\}\; (x)\; \backslash \; ldots\; p\_\; \{n-1\}\; (x)\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; mathsf\; \{T\}\}\}$, $ru\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{n\}\}$- это $n\; \{\backslash \; displaystyle\; n\}$-й стандартный базисный вектор, например, $en\; =\; [0\dots \; 0\; 1]\; T\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{e\}\; \_\; \{n\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 0\; \backslash \; ldots\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{\backslash \; mathsf\; \{T\}\}\}$, а J - так называемая матрица Якоби:

$J\; =\; (a\; 0\; 1\; 0\; \dots \dots \dots \; B\; 1\; a\; 1\; 1\; 0\; \dots \dots \; 0\; b\; 2\; a\; 2\; 1\; 0\dots \; 0\; \dots \dots \dots \dots \; 0\; \dots \dots \; 0\; млрд\; -\; 2\; an\; -\; 2\; 1\; \dots \dots \dots \; 0\; млрд\; -\; 1\; an\; -\; 1)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; a\_\; \{0\}\; 1\; 0\; \backslash \; ldots\; \backslash \; ldots\; \backslash \; ldots\; \backslash \backslash \; b\_\; \{1\}\; a\_\; \{1\}\; 1\; 0\; \backslash \; ldots\; \backslash \; ldots\; \backslash \backslash \; 0\; b\; \_\; \{2\}\; a\_\; \{2\}\; 1\; 0\; \backslash \; ldots\; \backslash \backslash \; 0\; \backslash \; ldots\; \backslash \; ldots\; \backslash \; ldots\; \backslash \; ldots\; 0\; \backslash \backslash \backslash \; ldots\; \backslash \; ldots\; 0\; b\_\; \{n-2\}\; a\_\; \{n-2\}\; 1\; \backslash \backslash \backslash \; ldots\; \backslash \; ldots\; \backslash \; ldots\; 0\; b\_\; \{n-1\}\; a\_\; \{n-1\}\; \backslash \; end\; \{pmatrix\}\}\}$

Нули $xj\; \{\; \backslash \; displaystyle\; x\_\; \{j\}\}$многочленов до степени n, которые используются в качестве узлов для квадратуры Гаусса, можно найти путем вычислений собственных значений трехдиагональной матрицы. Эта процедура известна как алгоритм Голуба - Велша.

Для весов и узлов рассматривать симметричную трехдиагональную матрицу $J\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{J\}\}\}$с элементами

$J\; i,\; i\; =\; J\; i,\; i\; =\; ai\; -\; 1\; i\; =\; 1,\dots ,\; n\; J\; i\; -\; 1,\; i\; =\; J\; i,\; i\; -\; 1\; =\; J\; i,\; i\; -\; 1\; J\; i\; -\; 1,\; i\; =\; bi\; -\; 1\; i\; =\; 2,\dots ,\; п.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; mathcal\; \{J\}\}\; \_\; \{i,\; i\}\; =\; J\_\; \{i,\; i\}\; =\; a\_\; \{i-1\}\; i\; =\; 1,\; \backslash \; ldots,\; n\; \backslash \backslash \; \{\backslash \; mathcal\; \{J\}\}\; \_\; \{i-1,\; i\}\; =\; \{\backslash \; mathcal\; \{J\}\}\; \_\; \{i,\; i-1\}\; =\; \{\backslash \; sqrt\; \{J\_\; \{i,\; i-1\}\; J\_\; \{i-1,\; i\}\; \}\}\; =\; \{\backslash \; sqrt\; \{b\_\; \{i-1\}\}\}\; i\; =\; 2,\; \backslash \; ldots,\; n.\; \backslash \; end\; \{align\}\}\}$

Jи $J\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{J\}\}\}$являются подобными матрицами и, следовательно, имеют одинаковые собственные значения ( узлы). Веса могут быть вычислены из соответствующих векторов: Если $\varphi \; (j)\; \{\backslash \; displaystyle\; \backslash \; phi\; ^\; \{(j)\}\}$является стандарлизованным собственным вектором (т. Е. Собственным вектором с евклидовой нормой, Связанного с величиной значения x j, соответствующее может быть вычислен из первого компонента этого вектора, а именно:

$wj\; =\; \mu \; 0\; (\varphi \; 1\; (j))\; 2\; \{\backslash \; displaystyle\; w\_\; \{j\}\; =\; \backslash \; mu\; \_\; \{0\}\; \backslash \; left\; (\backslash \; phi\; \_\; \{1\}\; ^\; \{(j)\}\; \backslash \; right)\; ^\; \{2\}\}$

где $\mu \; 0\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{\; 0\}\}$- интеграл весовой функции

$\mu \; 0\; =\; \int \; ab\; \omega \; (x)\; dx.\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{0\}\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; dx.\}$

См., например, (Gil, Segura Temme 2007) для получения дополнительной информации.

Оценки ошибок

Ошибку квадратурного правила Гаусса можно сформулировать следующим образом (Stoer Bulirsch 2002, Thm 3.6.24). Для подынтегрального выражения, имеющего 2n непрерывных производных,

$\int \; a\; b\; \omega \; (x)\; f\; (x)\; d\; x\; -\; \sum \; i\; =\; 1\; n\; w\; i\; f\; (x\; i)\; =\; f\; (2\; n)\; (\xi )\; (2\; n)!\; (пн,\; пн)\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; \backslash ,\; f\; (x)\; \backslash ,\; dx-\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; w\_\; \{i\}\; \backslash ,\; f\; (x\_\; \{i\})\; =\; \{\backslash \; frac\; \{f\; ^\; \{(2n)\}\; (\backslash \; xi)\}\; \{(2n)!\}\}\; \backslash ,\; (p\_\; \{n\},\; p\_\; \{n\})\}$

для некоторый ξ в (a, b), где p n - монический (т.е. старший коэффициент соотношения 1) ортогональный многочлен степени n и где

$(f,\; g)\; =\; \int \; ab\; \omega \; (x)\; f\; (x)\; g\; (x)\; dx.\; \{\backslash \; displaystyle\; (f,\; g)\; =\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \backslash \; omega\; (x)\; f\; (x)\; g\; (x)\; \backslash ,\; dx.\}$

В важном частном случае ω (x) = 1, у нас есть оценка ошибки (Kahaner, Moler Nash 1989, §5.2)

Стоер и Булирш замечают, что эта оценка неудобна на практике, так как может быть трудно оценить производную процедуру 2n, и, кроме того, фактическая ошибка может быть намного меньше, чем оценка, установленная производной. Другой подход заключается в использовании двухквадратных правил Гаусса разного порядка и оценки ошибки как разницы между двумя результатами. Для этой цели могут быть полезны квадратные правила Гаусса - Кронрода.

Правила Гаусса - Кронрода

Если интервал [a, b] разделен, оценки Гаусса новых подинтервалов никогда не совпадают с предыдущими точками оценки (за исключением нуля для нечетных чисел), поэтому подынтегральное выражение необходимо вычислять в каждой точке. Правила Гаусса.. Разница между квадратурным правилом Гаусса и его расширением Кронрода часто используется как оценка ошибки приближения.

правила Гаусса - Лобатто

Также известна как квадратура Лобатто (Abramowitz Stegun 1972, p. 888) harv error: no target: CITEREFAbramowitzStegun1972 (справка ), названный в честь голландского математика Рехуэля Лобатто. Он похож на квадратуру Гаусса со следующими отличиями:

1. Точки интегрирования включают в себя конечные точки интервала интегрирования.
2. Это верно для многочленов до степени 2n - 3, где n - количество точек интегрирования (Quarteroni, Sacco Saleri 2000).

квадратура Лобатто функции f (x) на интервале [−1, 1] :

$\int \; -\; 1\; 1\; f\; (x)\; dx\; =\; 2\; n\; (n\; -\; 1)\; [е\; (1)\; +\; е\; (-\; 1)]\; +\; \sum \; я\; знак\; равно\; 2\; n\; -\; 1\; wif\; (xi)\; +\; R\; n.\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{-\; 1\}\; ^\; \{1\}\; \{f\; (x)\; \backslash ,\; dx\}\; =\; \{\backslash \; frac\; \{2\}\; \{n\; (n-1)\}\}\; [f\; (1)\; +\; f\; (-1)\; ]\; +\; \backslash \; sum\; \_\; \{i\; =\; 2\}\; ^\; \{n-1\}\; \{w\_\; \{i\}\; f\; (x\_\; \{i\})\}\; +\; R\_\; \{n\}.\}$

Абсцисса: x i - это $(я\; -\; 1)\; \{\backslash \; displaystyle\; (i-1)\}$й ноль из $P\; n\; -\; 1\; \prime \; (x)\; \{\backslash \; displaystyle\; P\; \text{'}\_\; \{n-1\}\; (\; x)\}$.

Веса:

$wi\; =\; 2\; n\; (n\; -\; 1)\; [P\; n\; -\; 1\; (xi)]\; 2,\; xi\; \ne \; \pm \; 1.\; \{\backslash \; Displaystyle\; w\_\; \{i\}\; =\; \{\backslash \; frac\; \{2\}\; \{n\; (n-1)\; \backslash \; left\; [P\_\; \{n-1\}\; \backslash \; left\; (x\_\; \{i\}\; \backslash \; right)\; \backslash \; right]\; ^\; \{2\}\}\},\; \backslash \; qquad\; x\_\; \{i\}\; \backslash \; neq\; \backslash \; pm\; 1.\}$

Остаток:

Некоторые из весов:

Количество точек, n	точек, x i	Веса, w i
$3\; \{\backslash \; displaystyle\; 3\}$	$0\; \{\backslash \; displaystyle\; 0\}$	$4\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{4\}\; \{3\}\}\}$
	$\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$	$1\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\; \}\; \{3\}\}\}$
$4\; \{\backslash \; displaystyle\; 4\}$	$\pm \; 1\; 5\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{1\}\; \{5\}\}\}\}$	$5\; 6\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{5\}\; \{6\}\}\}$
	$\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$	$1\; 6\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{6\}\}\}$
$5\; \{\backslash \; displaystyle\; 5\}$	$0\; \{\backslash \; displaystyle\; 0\}$	$32\; 45\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{32\}\; \{45\}\}\}$
	$\pm \; 3\; 7\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{3\}\; \{7\; \}\}\}\}$	$49\; 90\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{49\}\; \{90\}\}\}$
	$\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$	$1\; 10\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\; 10\}\}\}$
$6\; \{\backslash \; displaystyle\; 6\}$	$\pm \; 1\; 3\; -\; 2\; 7\; 21\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{3\}\}\; -\; \{\backslash \; гидроразрыв\; \{2\; \{\backslash \; sqrt\; \{7\}\}\}\; \{21\}\}\}\}\}$	$14\; +\; 7\; 30\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{14\; +\; \{\backslash \; sqrt\; \{7\}\}\}\; \{30\}\}\}$
	$\pm \; 1\; 3\; +\; 2\; 7\; 21\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{3\}\}\; +\; \{\backslash \; frac\; \{2\; \{\backslash \; sqrt\; \{7\}\}\}\; \{21\}\}\}\}\}$	$14–7\; 30\; \{\; \backslash \; displaystyle\; \{\backslash \; frac\; \{14\; -\; \{\backslash \; sqrt\; \{7\}\}\}\; \{30\}\}\}$
	$\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$	$1\; 15\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{15\}\}\}$
$7\; \{\backslash \; displaystyle\; 7\}$	$0\; \{\backslash \; displaystyle\; 0\}$	$256\; 525\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{256\}\; \{525\}\}\}$
	$\pm \; 5\; 11\; -\; 2\; 11\; 5\; 3\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{5\}\; \{11\}\}\; -\; \{\backslash \; frac\; \{2\}\; \{11\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{5\}\; \{3\}\}\}\}\}\}$	$124\; +\; 7\; 15\; 350\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{124\; +\; 7\; \{\backslash \; sqrt\; \{15\}\}\; \}\; \{350\}\}\}$
	$\pm \; 5\; 11\; +\; 2\; 11\; 5\; 3\; \{\backslash \; displaystyle\; \backslash \; pm\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{5\}\; \{11\}\}\; +\; \{\backslash \; frac\; \{2\}\; \{11\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{5\}\; \{3\}\}\}\}\}\}$	$124–7\; 15\; 350\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{124-7\; \{\backslash \; sqrt\; \{15\}\}\}\; \{350\}\}\}$
	$\pm \; 1\; \{\backslash \; displaystyle\; \backslash \; pm\; 1\}$	$1\; 21\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{21\}\}\}$

Адаптивный вариант этого алгоритма с двумя внутренними узлами находится в GNU Octave и MATLAB as quadlи интегрировать.

• Реализация точного обобщенного квадратурного решения по Гауссу для поиска упругого поля в однородной анизотропной среде
• Абрамовиц, Милтон ; Стегун, Ирен Энн, ред. (1983) [июнь 1964]. «Глава 25.4, Интеграция». Справочник по математическим функциям с формулами, графиками и математическими таблицами. Прикладная математика. 55 (Девятое переиздание с дополнительными исправлениями; десятое оригинальное издание с исправлениями (декабрь 1972 г.); первое изд.). Вашингтон.; Нью-Йорк: Министерство торговли США, Национальное бюро стандартов; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
• Андерсон, Дональд Г. (1965). "Квадратурные формулы Гаусса для $\int \; 0\; 1\; -\; ln\; \; (x)\; f\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; -\; \backslash \; ln\; (x)\; f\; (x)\; dx\}$". Math. Comp. 19 (91): 477–481. doi : 10.1090 / s0025-5718-1965-0178569-1.
• Голуб, Джин Х. ; Уэлш, Джон Х. (1969), «Вычисление квадратурных правил Гаусса», «Математика вычислений», 23 (106): 221–230, doi : 10.1090 / S0025-5718-69-99647-1, JSTOR 2004418
• Гаучи, Уолтер (1968). «Построение квадратурных формул Гаусса – Кристоффеля». Math. Comp. 22 (102). Pp. 251–270. doi : 10.1090 / S0025-5718-1968-0228171-0. MR 0228171.
• Gautschi, Walter (1970). «О построении квадратурных правил Гаусса на основе модифицированных моментов». Math. Comp. 24 . Pp. 245–260. doi : 10.1090 / S0025-5718-1970-0285117-6. MR 0285177.
• Писсенс, Р. (1971). «Квадратурные формулы Гаусса для численного интегрирования интеграла Бромвича и обращения преобразования Лапласа». J. Eng. Математика. 5 (1). С. 1–9. Полномочный код : 1971JEnMa... 5.... 1P. doi : 10.1007 / BF01535429.
• Данлой, Бернард (1973). "Численное построение квадратурных формул Гаусса для $\int \; 0\; 1\; (-\; log\; \; x)\; x\; \alpha \; f\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; (-\; \backslash \; log\; x)\; x\; ^\; \{\backslash \; альфа\}\; f\; (x)\; dx\}$и $\int \; 0\; \infty \; E\; m\; (x)\; f\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; E\_\; \{m\}\; (\; x)\; f\; (x)\; dx\}$". Математика. Комп. 27 (124). С. 861–869. doi : 10.1090 / S0025-5718-1973-0331730-X. MR 0331730.
• Каханер, Дэвид; Молер, Клив ; Нэш, Стивен (1989), Числовой Методы и программное обеспечение, Прентис-Холл, ISBN 978-0-13-627258-8
• Сагар, Робин П. (1991). «Квадратура Гаусса для вычисления обобщенных интегралов Ферми-Дирака». Comput. Phys. Commun. 66 (2–3): 271–275. Bibcode : 1991CoPhC.. 66..271S. doi : 10.1016 / 0010-4655 (91) 90076-W.
• Якимив, Э. (1996). «Точное вычисление весов в классической системе Гаусса. Квадратурные правила Кристоффеля ". J. Comput. Phys. 129 (2): 406–430. Bibcode : 1996JCoPh.129..406Y. doi : 10.1006 / jcph.1996.0258.
• Лори, Дирк П. (1999), «Точное восстановление коэффициентов рекурсии из G квадратурные формулы Аусса», J. Comput. Appl. Math., 112 (1-2): 165-180, doi : 10.1016 / S0377-0427 (99) 00228-9
• Лори, Дирк П. (2001). «Вычисление квадратурных формул типа Гаусса». J. Comput. Appl. Математика. 127 (1-2): 201-217. Bibcode : 2001JCoAM.127..201L. doi : 10.1016 / S0377-0427 (00) 00506-9.
• Райнер, Кордиан; Швайгхофер, Маркус (2018). «Оптимизационные подходы к квадратуре: новые 45 : 22–54. arXiv : характеристики квадратур Гаусса на прямом и квадратном пространстве узлами на плоских алгебраических кривых, на плоскости и в более высоких измерений ». 1607.08404. doi : 10.10 16 / j.jco.2017.10.002.
• Стоер, Йозеф; Bul