Тройной график

редактировать

Барицентрический график по трем переменным

A тройной график, троичный график, треугольный график, симплексный график, треугольник Гиббса или диаграмма де Финетти . барицентрический график с тремя переменными, которые суммируют с константой. Он графически отображает отношения трех переменных в виде позиций в равностороннем треугольнике. Он используется в физической химии, петрологии, минералогии, металлургии и других физических науках, чтобы показать состав систем, состоящих из трех виды. В популяционной генетике ее часто называют диаграммой де Финетти. В теории игр это часто называют симплексным сюжетом. Тернарные графики - это инструменты для анализа композиционных данных в трехмерном случае.

Примерные цвета сплавов Ag – Au – Cu при изготовлении ювелирных изделий

На тройном графике значения трех переменных a, b и c должны суммироваться с некоторой константой K. Обычно эта константа представлена как 1.0 или 100%. Поскольку a + b + c = K для всех графически отображаемых веществ, любая переменная не является независимой от других, поэтому для нахождения точки образца на графике необходимо знать только две переменные: например, c должно быть равно K - а - б. Поскольку три числовых значения не могут изменяться независимо - есть только две степени свободы - можно изобразить комбинации всех трех переменных только в двух измерениях.

Содержание

1 Считывание значений на троичном графике
2 Вывод из декартовых координат
3 Построение троичного графика
4 Пример
- 4.1 Нанесение точек
5 См. Также
6 Ссылки
7 Внешние ссылки

Считывание значений на тройном графике

Преимущество использования троичного графика для изображения химического состава состоит в том, что три переменные могут быть удобно отображены в двумерный граф. Тройные графики также можно использовать для создания фазовых диаграмм путем выделения областей состава на графике, где существуют различные фазы.

Каждая точка на тройном графике представляет различный состав трех компонентов.

Параллель стороне треугольника - геометрическое место точек, представляющих системы с постоянным химическим составом в компоненте, расположенном в вершине, противоположной стороне.

Для определения соотношения трех видов в составе используются три общих метода.

Первый метод - это оценка на основе сетки фазовой диаграммы. Концентрация каждого вида составляет 100% (чистая фаза) в каждом углу треугольника и 0% на линии напротив него. Как видно на рисунках 3–8, процентное содержание определенного вида линейно уменьшается с увеличением расстояния от этого угла. Рисуя параллельные линии через равные промежутки между нулевой линией и углом (как видно на изображениях), можно установить тонкие границы для облегчения оценки содержания вида. Для данной точки фракция каждого из трех материалов в композиции может быть определена первым.

Для фазовых диаграмм, не содержащих линий сетки, самый простой способ определить композицию - установить высоту треугольника на 100% и определить кратчайшие расстояния от интересующей точки до каждой из трех сторон.. Согласно теореме Вивиани, расстояния (отношение расстояний к общей высоте 100%) дают содержание каждого из видов, как показано на рисунке 1.

Третий метод основан на большем количестве измерений, но не требует нанесения перпендикулярных линий. Прямые линии проводятся от каждого угла через интересующую точку к противоположной стороне треугольника. Длины этих линий, а также длины отрезков между точкой и соответствующими сторонами измеряются индивидуально. Соотношения затем можно определить, разделив эти сегменты на всю соответствующую линию, как показано на рисунке 2. (Сумма соотношений должна составлять 1).

Рисунок 1. Высотный метод
Рисунок 2. Метод пересечения
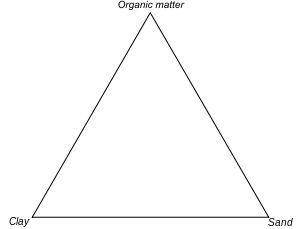
Рисунок 3. Пример тройной диаграммы без нанесенных точек.
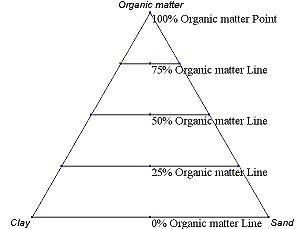
Рисунок 4. Пример тройной диаграммы, показывающий приращения по первой оси.
Рисунок 5. Пример тройной диаграммы, показывающий приращения по второй оси.
Рис. 6. Пример троичной диаграммы, показывающий приращения по третьей оси.
Рисунок 7. Пустой троичный график
Рисунок 8. Индикация того, как работают три оси.

Вывод из декартовых координат

Вывод тройного графика из декартовых координат

На рисунке (1) показана наклонная проекция точки P (a, b, c) в трехмерном Декартово пространство с осями a, b и c соответственно.

Если a + b + c = K (положительная константа), P ограничивается плоскостью, содержащей A (K, 0,0), B (0, K, 0) и C (0,0, К). Если a, b и c не могут быть отрицательными, P ограничивается треугольником, ограниченным A, B и C, как в (2).

В (3) оси повернуты для получения изометрического вида. Треугольник, если смотреть лицом вверх, выглядит равносторонним.

В (4) расстояния P от прямых BC, AC и AB обозначены как a ', b' и c 'соответственно.

Для любой строки l= s+ t n̂ в векторной форме (n̂ - единичный вектор) и точки p, перпендикулярное расстояние от p до l равно

‖ (s - p) - ((s - p) ⋅ n ^) n ^ ‖. {\ displaystyle \ left \ | (\ mathbf {s} - \ mathbf {p}) - {\ bigl (} (\ mathbf {s} - \ mathbf {p}) \ cdot \ mathbf {\ hat {n}} {\ bigr)} \ mathbf {\ hat {n}} \ right \ | \,.}

{\ displaystyle \ left \ | (\ mathbf {s} - \ mathbf {p}) - {\ bigl (} (\ mathbf {s} - \ mathbf {p}) \ cdot \ mathbf {\ hat {n}} {\ bigr)} \ mathbf {\ hat {n}} \ справа \ | \,.}

В этом случае точка P находится в

p = (abc). {\ displaystyle \ mathbf {p} = {\ begin {pmatrix} a \\ b \\ c \ end {pmatrix}} \,.}

{\ displaystyle \ mathbf {p} = {\ begin {pmatrix} a \\ b \\ c \ end {pmatrix}} \,.}

Линия BC имеет

s = (0 K 0) и n ^ = (0 K 0) - (0 0 K) ‖ (0 K 0) - (0 0 K) ‖ = (0 K - K) 0 2 + K 2 + (- K) 2 = (0 1 2 - 1 2). {\ displaystyle \ mathbf {s} = {\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} \ quad {\ text {and}} \ quad \ mathbf {\ hat {n}} = { \ frac {{\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} - {\ begin {pmatrix} 0 \\ 0 \\ K \ end {pmatrix}}} {\ left \ | {\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} - {\ begin {pmatrix} 0 \\ 0 \\ K \ end {pmatrix}} \ right \ |}} = {\ frac {\ begin {pmatrix} 0 \\ K \\ - K \ end {pmatrix}} {\ sqrt {0 ^ {2} + K ^ {2} + {(- K)} ^ {2}}}} = {\ begin {pmatrix} 0 \\ {\ frac {1} {\ sqrt {2}}} \\ - {\ frac {1} {\ sqrt {2}}} \ end {pmatrix}} \,.}

{\ displaystyle \ mathbf {s} = {\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} \ quad {\ текст {и}} \ quad \ mathbf {\ hat {n}} = {\ frac {{\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} - {\ begin {pmatrix} 0 \\ 0 \\ K \ end {pmatrix}}} {\ left \ | {\ begin {pmatrix} 0 \\ K \\ 0 \ end {pmatrix}} - {\ begin {pmatrix} 0 \\ 0 \\ K \ конец {pmatrix}} \ right \ |}} = {\ frac {\ begin {pmatrix} 0 \\ K \\ - K \ end {pmatrix}} {\ sqrt {0 ^ {2} + K ^ {2} + {(- K)} ^ {2}}}} = {\ begin {pmatrix} 0 \\ {\ frac {1} {\ sqrt {2}}} \\ - {\ frac {1} {\ sqrt {2}}} \ end {pmatrix}} \,.}

Используя формулу перпендикулярного расстояния,

a ′ = ‖ (- a K - b - c) - ((- a K - b - c) ⋅ (0 1 2 - 1 2)) (0 1 2 - 1 2) ‖ = ‖ (- a K - b - c) - (0 + K - b 2 + c 2) (0 1 2 - 1 2) ‖ = ‖ (- a K - b - K - b + c 2 - c + K - b + c 2) ‖ = ‖ (- a K - b - c 2 K - b - c 2) ‖ = (- a) 2 + (K - b - c 2) 2 + (K - b - c 2) 2 = a 2 + (K - b - c) 2 2. {\ displaystyle {\ begin {align} a '= \ left \ | {\ begin {pmatrix} -a \\ Kb \\ - c \ end {pmatrix}} - \ left ({\ begin {pmatrix} -a \\ Kb \\ - c \ end {pmatrix}} \ cdot {\ begin {pmatrix} 0 \\ {\ frac {1} {\ sqrt {2}}} \\ - {\ frac {1} {\ sqrt {2}}} \ end {pmatrix}} \ right) {\ begin {pmatrix} 0 \\ {\ frac {1} {\ sqrt {2}}} \\ - {\ frac {1} {\ sqrt { 2}}} \ end {pmatrix}} \ right \ | \\ [10px] = \ left \ | {\ begin {pmatrix} -a \\ Kb \\ - c \ end {pmatrix}} - \ left ( 0 + {\ frac {Kb} {\ sqrt {2}}} + {\ frac {c} {\ sqrt {2}}} \ right) {\ begin {pmatrix} 0 \\ {\ frac {1} { \ sqrt {2}}} \\ - {\ frac {1} {\ sqrt {2}}} \ end {pmatrix}} \ right \ | \\ [10px] = \ left \ | {\ begin {pmatrix } -a \\ Kb - {\ frac {K-b + c} {2}} \\ - c + {\ frac {K-b + c} {2}} \ end {pmatrix}} \ right \ | = \ left \ | {\ begin {pmatrix} -a \\ {\ frac {Kbc} {2}} \\ {\ frac {Kbc} {2}} \ end {pmatrix}} \ right \ | \\ [10px ] = {\ sqrt {{(-a)} ^ {2} + {\ left ({\ frac {Kbc} {2}} \ right)} ^ {2} + {\ left ({\ frac {Kbc } {2}} \ right)} ^ {2}}} = {\ sqrt {a ^ {2} + {\ frac {{(Kbc)} ^ {2}} {2}}}} \,. \ конец {выровнен}}}

{\begin{aligned}a'=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left({\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}\cdot {\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left(0+{\frac {K-b}{\sqrt {2}}}+{\frac {c}{\sqrt {2}}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]=\left\|{\begin{pmatrix}-a\\K-b-{\frac {K-b+c}{2}}\\-c+{\frac {K-b+c}{2}}\end{pmatrix}}\right\|=\left\|{\begin{pmatrix}-a\\{\frac {K-b-c}{2}}\\{\frac {K-b-c}{2}}\end{pmatrix}}\right\|\\[10px]={\sqrt {{(-a)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}}}={\sqrt {a^{2}+{\frac {{(K-b-c)}^{2}}{2}}}}\,.\end{aligned}}

Подставляя K = a + b + c,

a ′ = a 2 + (a + b + c - b - c) 2 2 = a 2 + a 2 2 = a 3 2. {\ displaystyle a '= {\ sqrt {a ^ {2} + {\ frac {{(a + b + cbc)} ^ {2}} {2}}}} = {\ sqrt {a ^ {2} + {\ frac {a ^ {2}} {2}}}} = a {\ sqrt {\ frac {3} {2}}} \,.}

a'={\sqrt {a^{2}+{\frac {{(a+b+c-b-c)}^{2}}{2}}}}={\sqrt {a^{2}+{\frac {a^{2}}{2}}}}=a{\sqrt {\frac {3}{2}}}\,.

Аналогичный расчет для линий AC и AB дает

b ′ = b 3 2 и c ′ = c 3 2. {\ displaystyle b '= b {\ sqrt {\ frac {3} {2}}} \ quad {\ text {and}} \ quad c' = c {\ sqrt {\ frac {3} {2}}} \,.}

b'=b{\sqrt {\frac {3}{2}}}\quad {\text{and}}\quad c'=c{\sqrt {\frac {3}{2}}}\,.

Это показывает, что расстояние от точки до соответствующих линий линейно пропорционально исходным значениям a, b и c.

Построение троичного графика

Декартовы координаты полезны для нанесения точек в треугольник. Рассмотрим равносторонний тройной график, где a = 100% помещается в (x, y) = (0,0), а b = 100% в (1,0). Тогда c = 100% равно (1/2, √3 / 2), а тройка (a, b, c) равна

(1 2 ⋅ 2 b + ca + b + c, 3 2 ⋅ ca + b + в). {\ displaystyle \ left ({\ frac {1} {2}} \ cdot {\ frac {2b + c} {a + b + c}}, {\ frac {\ sqrt {3}} {2}} \ cdot {\ frac {c} {a + b + c}} \ right) \,.}

{\ displaystyle \ left ({\ frac {1} {2}} \ cdot {\ frac {2b + c} {a + b + c}}, {\ frac {\ sqrt {3}} {2}} \ cdot {\ frac {c} {a + b + c}} \ right) \,.}

Пример

Раскрашенный текстурный треугольник почвы из Министерства сельского хозяйства США

В этом примере как это работает для гипотетического набора из трех образцов почвы:

Образец	Глина	Пилю	Песок	Примечания
Образец 1	50%	20%	30%	Поскольку глина и ил вместе составляют 70% этого образца, доля песка должна составлять 30%. для компонентов суммировать до 100%.
Образец 2	10%	60%	30%	Доля песка составляет 30%, как в Образце 1, но как доля ила увеличивается на 40%, соответственно уменьшается доля глины.
Образец 3	10%	30%	60%	Этот образец содержит ту же долю глины, что и Образец 2, но пропорции ил и песок меняются местами; график отражается относительно его вертикальной оси.

Нанесение точек

Образец 1 (1): Найдите линию с 50% глиной
Образец 1 (2): Найдите линию 20% ила
Образец 1 (3): пересечение совпадает с линией 30% песка, так как это математически зависит от первых двух
Нанесение всех образцов

См. также

Ссылки

Внешние ссылки

«Шаблон Excel для Тернарные диаграммы ». serc.carleton.edu. Научно-образовательный ресурсный центр (SERC) Карлтонский колледж. Проверено 14 мая 2020 г.
«Tri-plot: Программное обеспечение для построения троичных диаграмм». www.lboro.ac.uk. Университет Лафборо - Географический факультет / Главная страница портала ресурсов>Tri-plot. Проверено 14 мая 2020 г.
«Генератор троичных графиков - быстро создавать тройные диаграммы в строке». www.ternaryplot.com. Проверено 14 мая 2020 г.
Голландия, Стивен (2016). «Анализ данных в науках о Земле - тройные диаграммы, разработанные на языке R». strata.uga.edu. Университет Джорджии. Проверено 14 мая 2020 года.

Викискладе есть материалы, связанные с тройными графиками.