Очевидное молярное свойство

редактировать

Кажущееся молярное свойство компонента раствора в смеси или растворе количество, определенное с целью изолировать вклад каждого компонента в неидеальность смеси. Он показывает изменение соответствующего свойства раствора (например, объем ), когда весь этот компонент добавляется в раствор, на моль добавленного компонента. Он описан как очевидный, потому что он, по-видимому, отражает молярные свойства этого компонента в растворе, при условии, что свойства других компонентов раствора, как предполагается, остаются постоянными во время добавления. Однако это предположение часто не оправдано, поскольку значения кажущихся молярных свойств компонента могут сильно отличаться от его молярных свойств в чистом состоянии.

Например, объем раствора, содержащего два компонента, обозначенных как растворитель и растворенное вещество, определяется как

V = V 0 + ϕ V 1 = V ~ 0 n 0 + ϕ V ~ 1 N 1 {\ Displaystyle V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = {\ tilde {V}} _ {0} n_ {0} + {} ^ {\ phi} {\ tilde {V}} _ {1} n_ {1} \,}

V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = {\ tilde {V}} _ {{0}} n _ {{0}} + {} ^ {\ phi} {\ тильда {V}} _ {1} n_ {1} \,

где V 0 - объем чистого растворителя перед добавлением растворенного вещества и $V ~ 0 {\ displaystyle {\ tilde {V}} _ {0}}$ ${\ tilde {V }} _ {{0}}$ его молярный объем (при той же температуре и давлении, что и раствор), n 0 - количество моль растворителя, $ϕ V ~ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \,}$ ${} ^ {\ phi} {\ tilde {V}} _ {1} \,$ - кажущийся молярный объем растворенного вещества, а n 1 - количество молей растворенного вещества в растворе. Разделив это отношение на молярное количество одного компонента, можно получить соотношение между кажущимся молярным свойством компонента и соотношением компонентов в смеси.

Это уравнение служит определением $ϕ V ~ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \,}$ ${} ^ {\ phi} {\ tilde {V}} _ {1} \,$ . Первый член равен объему того же количества растворителя без растворенного вещества, а второй член - это изменение объема при добавлении растворенного вещества. $ϕ V ~ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \,}$ ${} ^ {\ phi} {\ tilde {V}} _ {1} \,$ может затем рассматриваться как молярный объем растворенного вещества, если он Предполагается, что молярный объем растворителя не изменяется при добавлении растворенного вещества. Однако это предположение часто следует считать нереалистичным, как показано в примерах ниже, так что $ϕ V ~ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \,}$ ${} ^ {\ phi} {\ tilde {V}} _ {1} \,$ описывается только как кажущееся значение.

Кажущееся молярное количество может быть аналогично определено для компонента, идентифицированного как растворитель $ϕ V ~ 0 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {0} \, }$ ${\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {0} \,}$ . Некоторые авторы сообщили об очевидных молярных объемах обоих (жидких) компонентов одного и того же раствора. Эту процедуру можно распространить на трехкомпонентные и многокомпонентные смеси.

Кажущиеся количества также могут быть выражены через массу вместо числа молей. Это выражение дает кажущиеся конкретные величины, такие как кажущийся удельный объем.

В знак равно В 0 + ϕ В 1 знак равно v 0 м 0 + ϕ v 1 м 1 {\ Displaystyle V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = v_ { 0} m_ {0} + {} ^ {\ phi} {v} _ {1} m_ {1} \,}

V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = v_ {0} m_ {0} + {} ^ {\ phi} {v} _ {1} m_ {1} \,

где конкретные количества обозначаются строчными буквами.

Кажущиеся (молярные) свойства не являются постоянными (даже при заданной температуре), а зависят от состава. При бесконечном разбавлении кажущееся молярное свойство и соответствующее частичное молярное свойство становятся равными.

Некоторые очевидные молярные свойства, которые обычно используются, включают кажущуюся молярную энтальпию, кажущуюся молярную теплоемкость и кажущийся молярный объем.

Содержание

1 Отношение к моляльности
2 Отношение к соотношению компонентов
3 Отношение к парциальным (молярным) количествам
4 Отношение к коэффициенту активности электролита и номеру его сольватационной оболочки
5 Примеры
- 5.1 Электролиты
- 5.2 Спирт
- 5.3 Электролит - неэлектролитные системы
6 Многокомпонентные смеси или растворы
7 См. Также
8 Ссылки
9 Внешние ссылки

Отношения к молярности

Кажущийся (молярный) объем растворенного вещества может быть выражен как функция моляльности b этого растворенного вещества (и от плотностей раствора и растворителя). Объем раствора на моль растворенного вещества составляет

1 ρ (1 b + M 1). {\ displaystyle {\ frac {1} {\ rho}} \ left ({\ frac {1} {b}} + M_ {1} \ right).}

{\ displaystyle {\ frac {1} {\ rho}} \ left ({\ frac {1} {b}} + M_ {1} \ right).}

Вычитание объема чистого растворителя на моль растворенного вещества дает кажущийся молярный объем:

ϕ V ~ 1 = 1 b (1 ρ - 1 ρ 0 0) + M 1 ρ {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} = {\ frac {1} {b}} \ left ({\ frac {1} {\ rho}} - {\ frac {1} {\ rho _ {0} ^ {0}}} \ right) + { \ frac {M_ {1}} {\ rho}}}

{\ displaystyle {} ^ {\ phi} {\ tilde { V}} _ {1} = {\ frac {1} {b}} \ left ({\ frac {1} {\ rho}} - {\ frac {1} {\ rho _ {0} ^ {0} }} \ right) + {\ frac {M_ {1}} {\ rho}}}

Для большего количества растворенных веществ приведенное выше равенство модифицировано средней молярной массой растворенных веществ, как если бы они были одним растворенным веществом с моляльностью b T:

ϕ V ~ 12.. = 1 б T (1 ρ - 1 ρ 0 0) + M ρ {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {12..} = {\ frac {1} {b_ {T}}} \ left ({\ frac {1} {\ rho}} - {\ frac {1} {\ rho _ {0} ^ {0}}} \ right) + {\ frac {M} { \ rho}}}

{\ displaystyle { } ^ {\ phi} {\ tilde {V}} _ {12..} = {\ frac {1} {b_ {T}}} \ left ({\ frac {1} {\ rho}} - {\ frac {1} {\ rho _ {0} ^ {0}}} \ right) + {\ frac {M} {\ rho}}}

M = ∑ yi M i {\ displaystyle M = \ sum y_ {i} M_ {i}}

{\ displaystyle M = \ sum y_ {i} M_ {i}}

Сумма молярностей продуктов - кажущийся молярный объем растворенных веществ в их бинарных растворах равен произведение между суммой молярностей растворенных веществ и кажущимся молярным объемом в тройном многокомпонентном растворе, упомянутом выше.

ϕ V ~ 123.. (b 1 + b 2 + b 3 +...) = b 1 ϕ V ~ 1 + b 2 ϕ V ~ 2 + b 3 ϕ V ~ 3 +... {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {123..} (b_ {1} + b_ {2} + b_ {3} +...) = b_ {1} {} ^ {\ phi} {\ tilde {V}} _ {1} + b_ {2} {} ^ {\ phi} {\ tilde {V}} _ {2} + b_ {3} {} ^ {\ phi } {\ tilde {V}} _ {3} +...}

{\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {123..} (b_ {1} + b_ {2} + b_ {3} +...) = b_ {1} {} ^ {\ phi} {\ tilde {V}} _ {1} + b_ {2} {} ^ {\ phi} {\ tilde {V}} _ {2} + b_ {3} {} ^ {\ phi} {\ tilde {V}} _ {3} +...}

Отношение к соотношению компонентов смеси

Отношение между кажущимся молярным соотношением компонента смеси и молярным соотношением компонентов смеси можно получить следующим образом: разделение отношения определения

V = V 0 + ϕ V 1 = V ~ 0 n 0 + ϕ V ~ 1 n 1 {\ displaystyle V = V_ {0} + {} ^ {\ phi} {V} _ { 1} \ = {\ tilde {V}} _ {0} n_ {0} + {} ^ {\ phi} {\ tilde {V}} _ {1} n_ {1} \,}

V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = {\ tilde {V}} _ {{0}} n _ {{0}} + {} ^ {\ phi} {\ тильда {V}} _ {1} n_ {1} \,

в количество молей одного компонента. Это дает следующее соотношение:

ϕ V ~ 1 = V n 1 - V ~ 0 n 0 n 1 = V n 1 - V ~ 0 r 01 {\ displaystyle {} ^ {\ phi} {\ tilde {V }} _ {1} = {\ frac {V} {n_ {1}}} - {\ tilde {V}} _ {0} {\ frac {n_ {0}} {n_ {1}}} = { \ frac {V} {n_ {1}}} - {\ tilde {V}} _ {0} r_ {01}}

{\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ { 1} = {\ frac {V} {n_ {1}}} - {\ tilde {V}} _ {0} {\ frac {n_ {0}} {n_ {1}}} = {\ frac {V } {n_ {1}}} - {\ tilde {V}} _ {0} r_ {01}}

Отношение к частным (молярным) количествам

Обратите внимание на разные определения между парциальное молярное количество и кажущееся молярное количество: в случае парциальных молярных объемов $V 0 ¯, V 1 ¯ {\ displaystyle {\ bar {V_ {0}}}, {\ bar {V_ {1}}}}$ ${\ displaystyle {\ bar {V_ {0}}}, {\ bar {V_ {1}}}}$ , определяемый

V 0 ¯ = (∂ V ∂ n 0) T, p, n 1, V 1 ¯ = (∂ V ∂ n 1) T, p, n 0 {\ displaystyle {\ bar {V_ {0}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {0}}} {\ Big)} _ {T, p, n_ {1}}, {\ bar {V_ {1}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {1}}} {\ Big)} _ {T, p, n_ {0}}}

{\ displaystyle {\ bar {V_ {0}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {0}}} {\ Big)} _ {T, p, n_ {1}}, {\ bar {V_ {1}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {1}}} {\ Big)} _ {T, p, n_ {0}}}

мы можем написать $d V = V 0 ¯ dn 0 + V 1 ¯ dn 1 {\ displaystyle dV = {\ bar {V_ {0}}} dn_ {0} + {\ bar {V_ {1) }}} dn_ {1}}$ ${\ displaystyle dV = {\ bar {V_ {0}}} dn_ {0} + {\ bar {V_ {1}}} dn_ {1}}$ , и поэтому $V = V 0 ¯ n 0 + V 1 ¯ n 1 {\ displaystyle V = {\ bar {V_ {0}}} n_ { 0} + {\ bar {V_ {1}}} n_ {1}}$ ${\ displaystyle V = {\ bar {V_ {0 }}} n_ {0} + {\ bar {V_ {1}}} n_ {1}}$ всегда хо lds. Напротив, при определении кажущегося молярного объема вместо этого используется молярный объем чистого растворителя, $V ~ 0 {\ displaystyle {\ tilde {V}} _ {0}}$ ${\ displaystyle {\ tilde {V}} _ {0}}$ , которое можно записать как

V 0 ~ = (∂ V ∂ n 0) T, p, n 1 = 0 {\ displaystyle {\ tilde {V_ {0}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {0}}} {\ Big)} _ {T, p, n_ {1} = 0}}

{\ displaystyle {\ tilde {V_ {0}}} = {\ Big (} {\ frac {\ partial V} {\ partial n_ {0}}} {\ Big)} _ {T, p, n_ {1} = 0}}

для сравнения. Другими словами, мы предполагаем, что объем растворителя не изменяется, и мы используем парциальный молярный объем, в котором количество молей растворенного вещества точно равно нулю («молярный объем»). Таким образом, в определяющем выражении для кажущегося молярного объема $ϕ V ~ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1}}$ ${\ displaystyle {} ^ {\ phi} {\ тильда {V}} _ {1}}$ ,

V = V 0 + ϕ V 1 Знак равно В ~ 0 N 0 + ϕ V ~ 1 N 1 {\ Displaystyle V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = {\ tilde {V}} _ {0} n_ {0} + {} ^ {\ phi} {\ tilde {V}} _ {1} n_ {1} \,}

V = V_ {0} + {} ^ {\ phi} {V} _ {1} \ = {\ tilde {V}} _ {{0}} n _ {{0}} + {} ^ {\ phi} {\ тильда {V}} _ {1} n_ {1} \,

термин $V 0 {\ displaystyle V_ {0}}$ $V_ {0}$ относится к чистому растворителю, а «оставшийся» избыточный объем, $ϕ V 1 {\ displaystyle {} ^ {\ phi} V_ {1}}$ ${\ displaystyle {} ^ {\ phi} V_ {1}}$ , считается происходят из растворенного вещества. При высоком разбавлении с $n 0 ≫ n 1 ≈ 0 {\ displaystyle n_ {0} \ gg n_ {1} \ приблизительно 0}$ ${ \ Displaystyle п_ {0} \ gg n_ {1} \ приблизительно 0}$ , мы имеем $V 0 ~ ≈ V 0 ¯ {\ displaystyle {\ tilde {V_ {0}}} \ приблизительно {\ bar {V_ {0}}}}$ ${\ displaystyle {\ tilde {V_ {0}}} \ приблизительно {\ bar {V_ {0}}}}$ , поэтому кажущийся молярный объем и парциальный молярный объем растворенного вещества также сходятся: $ϕ V ~ 1 ≈ V ¯ 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \ приблизительно {\ bar {V}} _ {1}}$ ${\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} \ приблизительно {\ bar {V}} _ {1}}$ .

Количественно, соотношение между частичными молярными свойствами и кажущимися свойствами может быть выведено из определения кажущихся величин и моляльности. Для объема

V 1 ¯ = ϕ V ~ 1 + b ∂ ϕ V ~ 1 ∂ b. {\ displaystyle {\ bar {V_ {1}}} = {} ^ {\ phi} {\ tilde {V}} _ {1} + b {\ frac {\ partial {} ^ {\ phi} {\ tilde {V}} _ {1}} {\ partial b}}.}

{\ bar {V_ {1} }} = {} ^ {\ phi} {\ tilde {V}} _ {1} + b {\ fr ac {\ partial {} ^ {\ phi} {\ tilde {V}} _ {1}} {\ partial b}}.

Отношение к коэффициенту активности электролита и номеру его сольватной оболочки

Отношение r a между кажущийся молярный объем растворенного электролита в концентрированном растворе и молярный объем растворителя (воды) могут быть связаны со статистической составляющей коэффициента активности электролита и его сольватационной оболочки число h:

$ln ⁡ γ s = h - ν ν ln ⁡ (1 + бюстгальтер 55,5) - h ν ln ⁡ (1 - бюстгальтер 55,5) + бюстгальтер (ra + h - ν) 55,5 (1 + бюстгальтер 55,5) {\ displaystyle \ ln \ gamma _ {s} = {\ frac {h- \ nu} {\ nu}} \ ln (1 + {\ frac {br_ {a}} {55.5}}) - {\ frac {h} {\ nu}} \ ln (1 - {\ frac {br_ {a}} {55.5}}) + {\ frac {br_ {a} (r_ {a} + h- \ nu)} {55,5 (1 + {\ frac {br_ {a}} {55.5}})}}}$ ${\ displaystyle \ ln \ gamma _ {s} = {\ frac {h- \ nu} {\ nu}} \ ln (1 + {\ frac {br_ {a}} {55.5}}) - {\ frac {h} {\ nu}} \ ln (1 - {\ frac {br_ {a}} {55.5}}) + {\ frac {br_ {a} (r_ {a} + h- \ nu)} {55,5 (1 + {\ frac {br_ {a}} {55.5}})}}}$ ,

где ν - количество ионов из-за диссоциации электролита.

Примеры

Электролиты

Кажущийся молярный объем соли обычно меньше, чем молярный объем твердой соли. Например, твердый NaCl имеет объем 27 см на моль, но кажущийся молярный объем при низких концентрациях составляет всего 16,6 см 3 / моль. Фактически, некоторые водные электролиты имеют отрицательные кажущиеся молярные объемы: NaOH -6,7, LiOH -6,0 и Na2CO3 -6,7 см / моль. Это означает, что их растворы в данном количестве воды имеют меньший объем, чем такое же количество чистой воды. (Однако эффект невелик.) Физическая причина в том, что близлежащие молекулы воды сильно притягиваются к ионам, поэтому они занимают меньше места.

Спирт

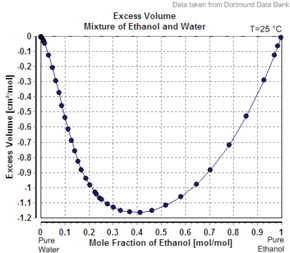
Избыточный объем смеси этанола и воды

Другим примером того, что кажущийся молярный объем второго компонента меньше его молярного объема как чистого вещества, является случай этанол в воде. Например, при 20 массовых процентах этанола раствор имеет объем 1,0326 л / кг при 20 ° C, а чистая вода составляет 1,0018 л / кг (1,0018 см3 / г).. Кажущийся объем добавленного этанола составляет 1,0326 л - 0,8 кг x 1,0018 л / кг = 0,2317 л. Количество моль этанола составляет 0,2 кг / (0,04607 кг / моль) = 4,341 моль, так что кажущийся молярный объем составляет 0,2317 L / 4,341 моль = 0,0532 л / моль = 53,2 см3 / моль (1,16 см3 / г). Однако чистый этанол имеет молярный объем при этой температуре 58,4 см 3 / моль (1,27 см 3 / г).

Если бы раствор был идеальным, его объем был бы суммой несмешанных компонентов. Объем 0,2 кг чистого этанола составляет 0,2 кг x 1,27 л / кг = 0,254 л, а объем 0,8 кг чистой воды составляет 0,8 кг x 1,0018 л / кг = 0,80144 л, поэтому идеальный объем раствора будет 0,254 л + 0,80144 L = 1,055 л. Неидеальность раствора отражается в небольшом уменьшении (примерно 2,2%, 1,0326, а не 1,055 л / кг) объема объединенной системы при смешивании. Когда процентное содержание этанола приближается к 100%, кажущийся молярный объем увеличивается до молярного объема чистого этанола.

Электролит - неэлектролитные системы

Очевидные количества могут подчеркивать взаимодействия в электролит-неэлектролитных системах, которые проявляют такие взаимодействия, как высаливание в и высаливание, но также дают представление о ионно-ионных взаимодействиях, особенно по их зависимости от температуры.

Многокомпонентные смеси или растворы

Для многокомпонентных растворов кажущиеся молярные свойства могут быть определены несколькими способами. Для объема тройного (3-компонентного) раствора с одним растворителем и двумя растворенными веществами в качестве примера все еще будет только одно уравнение $(V = V ~ 0 n 0 + ϕ V ~ 1 n 1 + ϕ V ~ 2 n 2) {\ displaystyle (V = {\ tilde {V}} _ {0} n_ {0} + {} ^ {\ phi} {\ tilde {V}} _ {1} n_ {1} + {} ^ {\ phi} {\ tilde {V}} _ {2} n_ {2})}$ ${\ displaystyle (V = {\ tilde {V}} _ {0} n_ {0} + {} ^ {\ phi} {\ tilde {V}} _ {1} n_ {1} + {} ^ {\ phi} {\ tilde {V}} _ {2} n_ {2})}$ , чего недостаточно для определения двух кажущихся объемов. (Это контрастирует с частичными молярными свойствами, которые являются четко определенными интенсивными свойствами материалов и поэтому однозначно определены в многокомпонентных системах. Например, парциальный молярный объем определяется для каждого компонент i как $V я ¯ = (∂ V / ∂ ni) T, p, nj ≠ i {\ displaystyle {\ bar {V_ {i}}} = (\ partial V / \ partial n_ {i}) _ {T, p, n_ {j \ neq i}}}$ ${\ displaystyle {\ бар {V_ {i}}} = (\ partial V / \ partial n_ {i}) _ {T, p, n_ {j \ neq i}}}$ .)

В одном описании тройных водных растворов рассматривается только средневзвешенный кажущийся молярный объем растворенных веществ, определяемый как

ϕ V ~ (n 1, n 2) = ϕ V ~ 12 = V - V 0 n 1 + n 2 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} (n_ {1}, n_ {2}) = {} ^ {\ phi} {\ tilde {V}} _ {12} = {\ frac {V-V_ {0}} {n_ {1} + n_ {2}}}}

{\ displaystyle {} ^ {\ phi} {\ tilde {V}} (n_ {1}, n_ {2}) = {} ^ {\ phi} {\ tilde { V}} _ {12} = {\ frac {V-V_ {0}} {n_ {1} + n_ {2}}}}

, где $V {\ displaystyle V}$ $V$ - объем раствора, а $V 0 {\ displaystyle V_ {0}}$ $V_ {0}$ - объем чистой воды. Этот метод может быть расширен для смесей, содержащих более трех компонентов.

ϕ V ~ (n 1, n 2, n 3,...) = Φ V ~ 123.. = V - V 0 n 1 + n 2 + п 3+... {\ displaystyle {} ^ {\ phi} {\ тильда {V}} (n_ {1}, n_ {2}, n_ {3},..) = {} ^ {\ phi} {\ tilde {V} } _ {123..} = {\ frac {V-V_ {0}} {n_ {1} + n_ {2} + n_ {3} +...}}}

{\ displaystyle {} ^ {\ phi} {\ тильда {V}} (n_ {1}, n_ {2}, n_ {3},..) = {} ^ {\ phi} {\ tilde {V}} _ {123..} = {\ frac {V-V_ {0}} {n_ {1} + n_ {2} + n_ {3} +...}}}

Сумма молярностей продуктов - кажущийся молярный объем растворенных веществ в их бинарных растворах равен произведению суммы молярностей растворенных веществ и кажущегося молярного объема в трехкомпонентном многокомпонентном растворе, упомянутом выше.

ϕ V ~ 123.. (b 1 + b 2 + b 3 +...) = b 1 ϕ V ~ 1 + b 2 ϕ V ~ 2 + b 3 ϕ V ~ 3 +... {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {123..} (b_ {1} + b_ {2} + b_ {3} +...) = b_ {1} {} ^ {\ phi} {\ tilde {V}} _ {1} + b_ {2} {} ^ {\ phi} {\ tilde {V}} _ {2} + b_ {3} {} ^ {\ phi } {\ tilde {V}} _ {3} +...}

{\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {123..} (b_ {1} + b_ {2} + b_ {3} +...) = b_ {1} {} ^ {\ phi} {\ tilde {V}} _ {1} + b_ {2} {} ^ {\ phi} {\ tilde {V}} _ {2} + b_ {3} {} ^ {\ phi} {\ tilde {V}} _ {3} +...}

Другой метод - рассматривать тройную систему как псевдобинарную и определять кажущийся молярный объем каждого растворенного вещества со ссылкой на бинарную систему, содержащую оба других компонента: вода и другие растворенные вещества. Тогда кажущиеся молярные объемы каждого из двух растворенных веществ равны

ϕ V ~ 1 = V - V (растворитель + растворенное вещество 2) n 1 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ { 1} = {\ frac {VV (растворитель + растворенное вещество \ 2)} {n_ {1}}}}

{\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {1} = {\ frac {VV (растворитель + растворенное вещество \ 2)} {n_ {1}}}}

ϕ V ~ 2 = V - V (растворитель + растворенное вещество 1) n 2 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {2} = {\ frac {VV (растворитель + растворенное вещество \ 1)} {n_ {2}}}}

{\ displaystyle {} ^ {\ phi } {\ тильда {V}} _ {2} = {\ frac {VV (растворитель + растворенное вещество \ 1)} {n_ {2}}}}

Кажущийся молярный объем растворителя:

$ϕ V ~ 0 = V - V (растворенное вещество 1 + растворенное вещество 2) n 0 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {0} = {\ frac {VV (растворенное вещество \ 1 + растворенное вещество \ 2)} {n_ {0}}}}$ ${\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ { 0} = {\ frac {VV (solute \ 1 + solu т. е. \ 2)} {п_ {0}}}}$

Однако это неудовлетворительное описание объемных свойств.

Кажущийся молярный объем двух рассматриваемых компонентов или растворенных веществ как один псевдокомпонент $ϕ V ~ 12 {\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {12}}$ ${\ displaystyle {} ^ {\ phi} { \ тильда {V}} _ {12}}$ или $ϕ V ~ ij {\ displaystyle { } ^ {\ phi} {\ tilde {V}} _ {ij}}$ ${\ displaystyle {} ^ {\ phi} {\ tilde {V}} _ {ij}}$ не следует путать с объемами частичных бинарных смесей с одним общим компонентом V ij, V jk который смешался с определенное соотношение смешивания формирует определенную тройную смесь V или V ijk.

Конечно, дополнительный объем компонента по отношению к другим компонентам смеси может быть определен как разница между объемом смеси и объем бинарной субмиксированной смеси данного состава, например:

$c V ~ 2 = V - V 01 n 2 {\ displaystyle {} ^ {c} {\ tilde {V}} _ {2} = {\ frac {V-V_ {01}} {n_ {2}}}}$ ${\ displaystyle {} ^ {c} {\ tilde {V}} _ {2} = {\ frac {V-V_ {01}} {n_ {2}}}}$

Бывают ситуации, когда нет строгого способа определить, какой растворитель, а какой растворенный, как в случае жидких смесей (скажем, вода и этанол), которые могут растворять или не растворять твердые вещества, такие как сахар или соль. В этих случаях кажущиеся молярные свойства можно и нужно приписывать всем компонентам смеси.

См. Также

Ссылки

^Данная маркировка является произвольно. Для смесей двух жидкостей любая может быть описана как растворитель. Для смесей жидкости и твердого вещества жидкость обычно идентифицируется как растворитель, а твердое вещество - как растворенное вещество, но теория все еще верна, если пометки поменять местами.
^Рок, Питер А., Химическая термодинамика, MacMillan 1969, стр.227-230 для смесей вода-этанол.
^Х. Г. Газоян и Ш. А. Маркарян (2014) ПЛОТНОСТЬ, ПРЕВЫШЕННЫЕ МОЛЯРНЫЕ И ЧАСТИЧНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ ДЛЯ ДИЭТИЛСУЛЬФОКСИДА С МЕТАНОЛОМ ИЛИ ЭТАНОЛОВЫМИ БИНАРНЫМИ СИСТЕМАМИ В ДИАПАЗОНЕ ТЕМПЕРАТУР 298,15 - 323,15 K ТРУДЫ ЕРЕВАНСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА, стр.17-25. См. Таблицу 4.
^Glueckauf, E. (1955). «Влияние ионной гидратации на коэффициенты активности в концентрированных растворах электролитов». Труды общества Фарадея. 51 : 1235–1244. doi : 10.1039 / TF9555101235.
^и "Физическая химия электролитических растворов", 1950, стр. 253.
^Рассчитано по данным Справочника CRC по химии и физике, 49-е издание.
^Лимонная кислота Апельблат, Александр (Springer 2014) стр.50 ISBN 978-3-319-11233-6
^Харнед, Оуэн, указ. соч. третье издание 1958 г., стр. 398-399
^Лимонная кислота Апельблат стр.320
^Апельблат стр.320

Внешние ссылки