Пятиугольник

редактировать

Многоугольник с 15 гранями

Правильный пятиугольник
Правильный пятиугольник
Тип	Правильный многоугольник
Ребра и вершины	15
символ Шлефли	{15}
диаграмма Кокстера
группа симметрии	двугранный (D15), порядок 2 × 15
внутренний угол (градусов )	156 °
Двойной многоугольник	Собственный
Свойства	Выпуклый, циклический, равносторонний, изогональный, изотоксальный

В геометрии пятиугольник или пятиугольник или 15-угольник представляет собой пятнадцатигранный многоугольник .

Содержание

1 Правильный пятиугольник
2 Использование
- 2.1 Конструкция
3 Симметрия
- 3.1 Пентадекаграммы
- 3.2 Многоугольники Петри
4 См. Также
5 Ссылки
6 Внешние ссылки

Правильный пятиугольник

A правильный пятиугольник представлен символом Шлефли {15}.

A Правильный пятиугольник имеет внутренние углы 156 ° и с длиной стороны a имеет площадь gi ven by

A = 15 4 a 2 детская кроватка ⁡ π 15 = 15 4 7 + 2 5 + 2 15 + 6 5 a 2 = 15 a 2 8 (3 + 15 + 2 5 + 5) ≃ 17.6424 a 2. {\ displaystyle {\ begin {align} A = {\ frac {15} {4}} a ^ {2} \ cot {\ frac {\ pi} {15}} = {\ frac {15} {4} } {\ sqrt {7 + 2 {\ sqrt {5}} + 2 {\ sqrt {15 + 6 {\ sqrt {5}}}}} a ^ {2} \\ = {\ frac {15a ^ {2}} {8}} \ left ({\ sqrt {3}} + {\ sqrt {15}} + {\ sqrt {2}} {\ sqrt {5 + {\ sqrt {5}}}} \ right) \\ \ simeq 17.6424 \, a ^ {2}. \ end {align}}}

{\ displaystyle {\ begin {выровнено } A = {\ frac {15} {4}} a ^ {2} \ cot {\ frac {\ pi} {15}} = {\ frac {15} {4}} {\ sqrt {7 + 2 {\ sqrt {5}} + 2 {\ sqrt {15 + 6 {\ sqrt {5}}}}}} a ^ {2} \\ = {\ frac {15a ^ {2}} {8}} \ left ({\ sqrt {3}} + {\ sqrt {15}} + {\ sqrt {2}} {\ sqrt {5 + {\ sqrt {5}}}} \ right) \\ \ simeq 17.6424 \, a ^ {2}. \ end {align}}}

Использует

. Правильный треугольник, десятиугольник и пятиугольник не могут полностью заполнить вершину плоскости.

Построение

Поскольку 15 = 3 × 5, произведение различных простых чисел Ферма, правильный пятиугольник можно построить с помощью циркуля и линейки : Следующие конструкции правильных пятиугольников с данной описанной окружностью похожи на иллюстрацию предложения XVI в Книге IV Элементов Евклида.

Обычный пятиугольник, начертанный кругом.gif

Сравните конструкцию Евклида на этом изображении: Пентадекагон

В конструкции для для данной описанной окружности: $FG ¯ = CF ¯, AH ¯ = GM ¯, | E 1 E 6 | {\ displaystyle {\ overline {FG}} = {\ overline {CF}} {\ text {,}} \; {\ overline {AH}} = {\ overline {GM}} {\ text {,}} \ ; | E_ {1} E_ {6} |}$ ${\ overline {FG}} = {\ overline {CF}} {\ text {,}} \; {\ overline {AH}} = {\ overline {GM}} {\ text {,} } \; | E_ {1} E_ {6} |$ - сторона равностороннего треугольника, а $| E 2 E 5 | {\ displaystyle | E_ {2} E_ {5} |}$ $| E_ {2} E_ {5} |$ - сторона правильного пятиугольника. Точка $H {\ displaystyle H}$ $H$ делит радиус $AM ¯ {\ displaystyle {\ overline {AM}}}$ ${\ overline {AM}}$ в золотом сечении : $AH ¯ HM ¯ = AM ¯ AH ¯ = 1 + 5 2 = Φ ≈ 1,618. {\ displaystyle {\ frac {\ overline {AH}} {\ overline {HM}}} = {\ frac {\ overline {AM}} {\ overline {AH}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ Phi \ приблизительно 1.618 {\ text {.}}}$ ${\ frac {\ overline {AH}} {\ overline {HM}}} = {\ frac {\ overline {AM}} {\ overline {AH}}} = {\ frac {1 + {\ sqrt {5}) }} {2}} = \ Phi \ приблизительно 1,618 {\ text {.}}$

По сравнению с первой анимацией (с зелеными линиями) на следующих двух изображениях две дуги окружности (для углов 36 ° и 24 °), повернутые на 90 ° против часовой стрелки. Они не используют сегмент $CG ¯ {\ displaystyle {\ overline {CG}}}$ ${\ displaystyle {\ overline {CG}}}$ , а используют сегмент $MG ¯ {\ displaystyle {\ overline {MG}}}$ ${\ displaystyle {\ overline {MG }}}$ как радиус $AH ¯ {\ displaystyle {\ overline {AH}}}$ ${\ displaystyle {\ overline {AH}}}$ для второй дуги окружности (угол 36 °).

Конструкция циркуля и линейки для заданной длины стороны. Конструкция почти такая же, как у пятиугольника на данной стороне, тогда презентация завершается расширением одной стороны и генерируется сегмент, здесь $FE 2 ¯, {\ displaystyle {\ overline {FE_ {2}}} {\ text {,}}}$ ${\ overline {FE_ {2}}} {\ text {,}}$ который разделен согласно золотому сечению:

$E 1 E 2 ¯ E 1 F ¯ = E 2 F ¯ E 1 E 2 ¯ = 1 + 5 2 = Φ ≈ 1,618. {\ displaystyle {\ frac {\ overline {E_ {1} E_ {2}}} {\ overline {E_ {1} F}}} = {\ frac {\ overline {E_ {2} F}} {\ overline {E_ {1} E_ {2}}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ Phi \ приблизительно 1,618 {\ text {.}}}$ ${\ frac {\ overline {E_ {1} E_ {2}}} {\ overline {E_ {1} F}}} = {\ frac {\ overline {E_ {2} F}} {\ overline {E_ { 1} E_ {2}}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ Phi \ приблизительно 1.618 {\ text {.}}$

Окружной радиус $E 2 M ¯ = R; {\ displaystyle {\ overline {E_ {2} M}} = R \ ;; \; \;}$ ${\ displaystyle {\ overline {E_ {2} M}} = R \ ;; \; \;}$ Длина стороны $E 1 E 2 ¯ = a; {\ displaystyle {\ overline {E_ {1} E_ {2}}} = a \ ;; \; \;}$ ${\ displaystyle {\ overline {E_ {1} E_ {2}}} = a \ ;; \; \;}$ Угол $DE 1 M = ME 2 D = 78 ∘ {\ displaystyle DE_ {1} M = ME_ {2} D = 78 ^ {\ circ}}$ ${\ displaystyle DE_ {1} M = ME_ {2} D = 78 ^ {\ circ}}$

$R = a ⋅ 1 2 ⋅ (5 + 2 ⋅ 5 + 3) = 1 2 ⋅ 8 + 2 ⋅ 5 + 2 15 + 6 ⋅ 5 ⋅ a = грех ⁡ (78 ∘) грех ⁡ (24 ∘) ⋅ a ≈ 2,40486 ⋅ a {\ displaystyle {\ begin {align} R = a \ cdot {\ frac {1} {2}} \ cdot \ left ({\ sqrt {5 + 2 \ cdot {\ sqrt {5}}}} + {\ sqrt {3}} \ right) = {\ frac {1} {2}} \ cdot {\ sqrt { 8 + 2 \ cdot {\ sqrt {5}} + 2 {\ sqrt {15 + 6 \ cdot {\ sqrt {5}}}}}} \ cdot a \\ = {\ frac {\ sin (78 ^ {\ circ})} {\ sin (24 ^ {\ circ})}} \ cdot a \ приблизительно 2.40486 \ cdot a \ end {align}}}$ ${\ displaystyle {\ begin {align} R = a \ cdot {\ frac {1} {2}} \ cdot \ left ({\ sqrt {5 + 2 \ cdot {\ sqrt {5}}}} + {\ sqrt {3}} \ right) = {\ frac {1} {2}} \ cdot {\ sqrt {8 + 2 \ cdot {\ sqrt {5}} + 2 {\ sqrt {15 + 6 \ cdot {\ sqrt {5}}}}}} \ c точка a \\ = {\ frac {\ sin (78 ^ {\ circ})} {\ sin (24 ^ {\ circ})}} \ cdot a \ приблизительно 2.40486 \ cdot a \ end {выравнивается}}}$

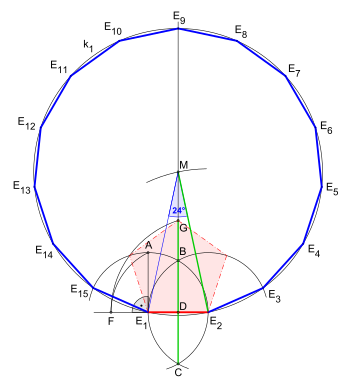Построение для заданной длины стороны

Построение для заданная длина стороны как анимация

Симметрия

Симметрии правильного пятиугольника, как показано с цветами на краях и вершинах. Линии отражений синие. Гирации указаны цифрами в центре. Вершины окрашены в соответствии с их положением симметрии.

Правильный пятиугольник имеет Dih 15двугранную симметрию, порядок 30, представленный 15 линиями отражения. Dih 15 имеет 3 двугранные подгруппы: Dih 5, Dih 3 и Dih 1. И еще четыре циклической симметрии: Z 15, Z 5, Z 3 и Z 1, с Z n представляет вращательную симметрию π / n в радианах.

На пятиугольнике есть 8 различных симметрий. Джон Конвей обозначает эти симметрии буквой, и порядок симметрии следует за буквой. Он дает r30 для полной отражательной симметрии, Dih 15. Он дает d (диагональ) с линиями отражения через вершины, p с линиями отражения через ребра (перпендикулярно), а также для нечетного пятиугольника i с зеркалом прямые, проходящие через вершины и ребра, и g для циклической симметрии. a1 означает отсутствие симметрии.

Эти более низкие симметрии позволяют степеням свободы определять неправильные пятиугольники. Только подгруппа g15 не имеет степеней свободы, но может рассматриваться как направленные ребра.

Пентадекаграммы

Есть три правильных звездчатых многоугольника : {15 / 2}, {15/4}, {15/7}, построенные из тех же 15 вершин правильного пятиугольника, но соединенные пропуском каждой второй, четвертой или седьмой вершины соответственно.

Есть также три обычных звездных фигуры : {15/3}, {15/5}, {15/6}, первая из которых состоит из трех пятиугольников, второй - соединение пяти равносторонних треугольников, а третий - соединение трех пентаграмм.

Составную фигуру {15/3} можно в общих чертах рассматривать как двумерный эквивалент трехмерного соединения пяти тетраэдров.

Рисунок	. {15/2}.	. {15/3} или 3 {5}	. {15/4}.	. {15/5 } или 5 {3}	. {15/6} или 3 {5/2}	. {15/7}.
Внутренний угол	132 °	108 °	84 °	60 °	36 °	12 °

Более глубокие усечения правильного пятиугольника и пентадекаграммы могут давать изогональные (вершинно-транзитивные ) промежуточный звездообразный многоугольник образует с равным расстоянием между вершинами и двумя длинами ребер.

Вершинно-транзитивные усечения пятиугольника
Квазирегулярные	Изогональные	Квазирегулярные
. t { 15/2} = {30/2}		. t {15/13} = {30/13}
. t {15/7} = {30/7}		. t {15/8} = {30/8}
. т {15/11} = {30/22}		. t {15/4} = {30/4}