Математические функции
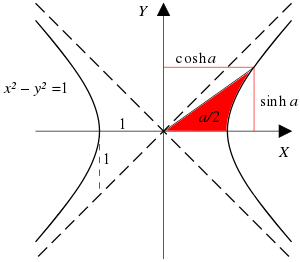
Луч сквозь
гиперболу единиц 
в точке

, где

- это удвоенная площадь между лучом, гиперболой, и

-axis

Обратные гиперболические функции
В математике обратные гиперболические функции являются обратными функциями для гиперболических функций.
Для данного значения гиперболической функции соответствующая обратная гиперболическая функция обеспечивает соответствующий гиперболический угол. Размер гиперболического угла равен площади соответствующего гиперболического сектора гиперболы xy = 1, или удвоенной площади соответствующего сектора единичной гиперболы . x - y = 1, так же, как круговой угол в два раза больше площади кругового сектора единичной окружности . Некоторые авторы назвали обратные гиперболические функции «функциями площади », чтобы реализовать гиперболические углы.
Гиперболические функции возникают при вычислениях углов и расстояний в гиперболической геометрии. Это также встречается в решениях многих линейных дифференциальных уравнений (например, уравнения, определяющего цепную связь ), кубических уравнений и уравнения Лапласа в декартовых координатах. Уравнения Лапласа важны во многих областях физики, включая электромагнитную теорию, теплопередачу, гидродинамику, и специальная теория относительности.
Содержание
- 1 Обозначение
- 2 Определения в терминах логарифмов
- 2.1 Обратный гиперболический синус
- 2.2 Обратный гиперболический косинус
- 2.3 Обратный гиперболический тангенс
- 2.4 Обратный гиперболический котангенс
- 2,5 Обратный гиперболический секанс
- 2,6 Обратный гиперболический косеканс
- 3 Формулы сложения
- 4 Другие тождества
- 5 Состав гиперболических и обратных гиперболических функций
- 6 Состав обратных гиперболических и тригонометрических функций
- 7 Преобразования
- 8 Производные
- 9 Расширения в ряды
- 10 Основные значения в комплексной плоскости
- 10.1 Главное значение обратного гиперболического синуса
- 10.2 Главное значение обратного гиперболического косинуса
- 10.3 Основные значения обратного гиперболического тангенса и котангенса
- 10.4 Главное значение обратного гипербола ic косеканс
- 10.5 Главное значение обратного гиперболического секанса
- 10.6 Графическое представление
- 11 См. также
- 12 Ссылки
- 13 Библиография
- 14 Внешние ссылки
Обозначения
Наиболее распространены сокращения, указанные в стандарте ISO 80000-2. Они состоят из ar-, за которым следует аббревиатура соответствующей гиперболической функции (например, arsinh, arcosh).
Однако arc-, за которым следует соответствующая гиперболическая функция (например, arcsinh, arccosh), также часто встречается по аналогии с номенклатурой для обратных тригонометрических функций. Первые неверны, поскольку префикс arc - это сокращение от arcus, а префикс ar означает площадь.
Другие авторы предпочитают использовать обозначения arg sinh, argcosh, argtanh и и так далее, где префикс arg - это сокращение от латинского argumentsum. В информатике это часто сокращается до asinh.
Также используются обозначения sinh (x), ch (x) и т. Д., Несмотря на то, что необходимо проявлять осторожность, чтобы избежать неправильного толкования надстрочного индекса −1 как степени, в отличие от сокращения для обозначения обратной функции (например, ch (x) по сравнению с ch (x)).
Определения в терминах логарифмов
Поскольку гиперболические функции являются рациональными функциями числа e, числитель и знаменатель которых имеют степень не выше двух, эти функции могут быть решены в терминах e с использованием квадратной формулы ; тогда, взяв натуральный логарифм, получим следующие выражения для обратных гиперболических функций.
Для сложных аргументов, обратные гиперболические функции, квадратный корень и логарифм являются многозначными функциями, а равенства следующие подразделы можно рассматривать как равенства многозначных функций.
Для всех обратных гиперболических функций (за исключением обратного гиперболического котангенса и обратного гиперболического косеканса) область определения действительной функции подключена.
Обратный гиперболический синус
Обратный гиперболический синус (также известный как площадь гиперболического синуса) (латинское: Area sinus hyperbolicus):

Домен - это вся вещественная линия.
Обратный гиперболический косинус
Обратный гиперболический косинус (также известный как гиперболический косинус площади) (Латинское: Area cosinus hyperbolicus):

Домен - это закрытый интервал [1, + ∞).
Обратный гиперболический тангенс
Обратный гиперболический тангенс (он же - гиперболический тангенс площади) (латинское: Area tangens hyperbolicus):

Домен это открытый интервал (-1, 1).
Обратный гиперболический котангенс
Обратный гиперболический котангенс (он же гиперболический котангенс площади) (латинское: Area cotangens hyperbolicus):

Домен есть объединение открытых интервалов (−∞, −1) и (1, + ∞).
Обратный гиперболический секанс
Обратный гиперболический секанс (он же гиперболический секанс площади) (латинское: Area secans hyperbolicus):

Область представляет собой полуоткрытый интервал (0, 1].
Обратный гиперболический косеканс
Обратный гиперболический косеканс (также известный как гиперболический косеканс площади) (латинское: Area cosecans hyperbolicus):

Домен - это вещественная линия с удаленным 0.
Формулы сложения




Другие тождества


Состав гиперболической и обратной гиперболической функций

Состав обратных гиперболических и тригонометрических функций


Преобразования




Производные

Для примера дифференцирования: пусть θ = arsinh x, поэтому (где sinh θ = (sh θ)):

Расширения серии
Расширения серии могут быть получены для вышеуказанных функций:





Асимптотическое разложение для арсина x дается выражением

.
Основные значения в комплексной плоскости
Как и функции комплексной переменной, обратные гиперболические функции - это многозначные функции, которые аналитичны, за исключением конечного числа точек. функция, обычно определяют главное значение, которое представляет собой однозначную аналитическую функцию, которая совпадает с одной конкретной ветвью многозначной функции, в области, состоящей из комплексной плоскости в котором было удалено конечное число дуг (обычно половинных линий или сегментов линии ). Эти дуги называются разветвлениями. Для указания ветви, то есть определения того, какое значение многозначной функции учитывается в каждой точке, обычно определяют ее в конкретной точке и выводят значение повсюду в области определения главного значения с помощью аналитического продолжения.. По возможности лучше определять главное значение напрямую, не обращаясь к аналитическому продолжению.
Например, для квадратного корня главное значение определяется как квадратный корень, имеющий положительную действительную часть. Это определяет однозначную аналитическую функцию, которая определена везде, за исключением неположительных действительных значений переменных (где два квадратных корня имеют нулевую действительную часть). Это главное значение функции квадратного корня обозначается в дальнейшем  . Точно так же главное значение логарифма, обозначаемое ниже
. Точно так же главное значение логарифма, обозначаемое ниже  , определяется как значение, для которого мнимая часть имеет наименьшее абсолютное значение. Он определен везде, кроме неположительных действительных значений переменной, для которых два разных значения логарифма достигают минимума.
, определяется как значение, для которого мнимая часть имеет наименьшее абсолютное значение. Он определен везде, кроме неположительных действительных значений переменной, для которых два разных значения логарифма достигают минимума.
Для всех обратных гиперболических функций главное значение может быть определено в терминах главных значений квадратного корня и функции логарифма. Однако в некоторых случаях формулы из § Определения в терминах логарифмов не дают правильного главного значения, так как дают область определения, которая слишком мала и в одном случае не связана.
Главное значение обратного гиперболического синуса
Главное значение обратного гиперболического синуса дается как

Аргумент квадратного корня не- положительное действительное число, если и только если z принадлежит одному из интервалов [i, + i∞) и (−i∞, −i] мнимой оси. Если аргумент логарифма действительный, то он положительный. Таким образом, эта формула определяет главное значение для arsinh с разрезами ветвления [i, + i∞) и (−i∞, −i]. Это оптимально, поскольку разрезы ветвей должны соединять особые точки i и −i с бесконечностью..
Главное значение обратного гиперболического косинуса
Формула для обратного гиперболического косинуса, приведенная в § Обратный гиперболический косинус не удобна, так как аналогична основным значениям логарифма и квадратного корня, главное значение arcosh не будет определено для мнимого z. Таким образом, квадратный корень необходимо разложить на множители, что приведет к

Определены главные значения квадратных корней, кроме случая, когда z принадлежит действительному интервалу (−∞, 1]. Если аргумент логарифма действительный, то z действительный и имеет тот же знак. Таким образом, приведенная выше формула определяет главное значение arcosh вне действительного интервала (−∞, 1], которое, таким образом, является единственным разрезом ветви.
Основные значения обратного гиперболического тангенса и котангенса
Формулы, приведенные в § Определения в терминах логарифмов предполагают

для определения главных значений обратного гиперболического тангенса и котангенса. В этих формулах аргумент логарифма является действительным тогда и только тогда, когда z является действительным. Для artanh этот аргумент находится в вещественный интервал (−∞, 0], если z принадлежит либо (−∞, −1], либо [1, ∞). Для arcoth аргумент логарифма находится в (−∞, 0], тогда и только тогда, когда z принадлежит действительному интервалу [−1, 1].
Таким образом, эти формулы определяют удобные главные значения, для которых сечения ветвей составляют (−∞, −1] и [1, ∞) для обратной гиперболической касательной и [−1, 1] для обратной гиперболический котангенс.
Ввиду лучшей числовой оценки вблизи сечений ветвей некоторые авторы используют следующие определения главных значений, хотя второе вводит устранимую особенность при z = 0. Два определения  для реальных значений
для реальных значений  отличаются от
отличаются от  . Значения
. Значения  отличаются для реальных значений
отличаются для реальных значений  с
с  .
.

Главное значение обратного гиперболического косеканса
Для обратного гиперболического косеканса главное значение определяется как
 .
.
Определяется, когда аргументы логарифма и квадратного корня не являются неположительными действительными числами. Таким образом, главное значение квадратного корня определяется вне интервала [−i, i] мнимой прямой. Если аргумент логарифма действительный, то z - ненулевое действительное число, и это означает, что аргумент логарифма положительный.
Таким образом, главное значение определяется приведенной выше формулой за пределами среза ветви, состоящей из интервала [-i, i] воображаемой линии.
Для z = 0 существует особая точка, которая включена в разрез ветви.
Главное значение обратного гиперболического секанса
Здесь, как и в случае обратного гиперболического косинуса, мы должны факторизовать квадратный корень. Это дает главное значение

Если аргумент квадратного корня действительный, то z действительный, и отсюда следует, что оба главных значения квадратных корней определены, за исключением случаев, когда z вещественное число и принадлежит одному из интервалов (−∞, 0] и [1, + ∞). Если аргумент логарифма действительный и отрицательный, то z также действительный и отрицательный. Отсюда следует, что главное значение arsech хорошо определено приведенной выше формулой вне двух отрезков ветвей , реальных интервалов (−∞, 0] и [1, + ∞).
При z = 0 существует особая точка, которая входит в одно из сечений ветви.
Графическое представление
В следующем графическом представлении основных значений обратных гиперболических функций сечения ветвей отображаются как разрывы цвета. Тот факт, что все сечения ветвей выглядят как разрывы, показывает, что эти главные значения не могут быть расширены до аналитических функций, определенных для более крупных областей. Другими словами, определенные выше отрезки ветвей минимальны.
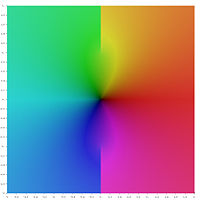

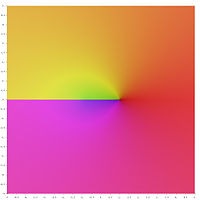

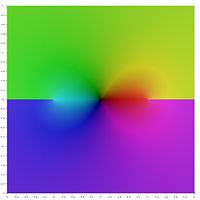

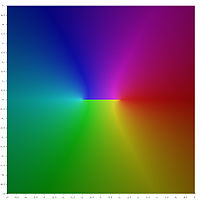





Обратные гиперболические функции в комплексной плоскости z: цвет в каждой точке плоскости
представляет комплексное значение соответствующей функции в этой точке
См. также
Ссылки
Библиография
- Герберт Буземан и Пол Дж. Келли (1953) Проективная геометрия и проективные метрики, стр. 207, Academic Press.
Внешние ссылки
 Луч сквозь гиперболу единиц
Луч сквозь гиперболу единиц  в точке
в точке  , где
, где  - это удвоенная площадь между лучом, гиперболой, и
- это удвоенная площадь между лучом, гиперболой, и  -axis
-axis  Обратные гиперболические функции
Обратные гиперболические функции 






































 .
.











 Обратные гиперболические функции в комплексной плоскости z: цвет в каждой точке плоскости представляет комплексное значение соответствующей функции в этой точке
Обратные гиперболические функции в комплексной плоскости z: цвет в каждой точке плоскости представляет комплексное значение соответствующей функции в этой точке