Геодезические на эллипсоиде

редактировать

Геодезические на сплющенном эллипсоиде

Изучение геодезических на эллипсоиде возникло в связи с с геодезией, а именно с решением сетей триангуляции. Фигура Земли хорошо аппроксимируется сплюснутым эллипсоидом, слегка сплющенной сферой. геодезическая - это кратчайший путь между двумя точками на изогнутой поверхности, аналогичный прямой линии на плоской поверхности. Таким образом, решение триангуляционной сети на эллипсоиде представляет собой набор упражнений по сфероидальной тригонометрии (Эйлер 1755).

Если Земля как сфера, геодезические - это большие круги (все они замкнуты), а проблемы сводятся к кругам в сферической тригонометрия. Ньютон (1687) показал, что эффект вращения Земли приводит к тому, что она напоминает слегка сплющенный эллипсоид экватор и меридианы - единственные простые замкнутые геодезические. Более того, кратчайший путь между точками на экваторе не обязательно проходит вдоль экватора. Наконец, если эллипсоид превущается, чтобы стать трехосным эллипсоидом (с тремя различными полуосями), замкнуты только три геодезические.

Содержание

1 Геодезические на эллипсоиде Площадь вращения
- 1.1 Уравнения для геодезических
- 1.2 Поведение геодезических
- 1.3 Дифференциальные свойства геодезических
- 1.4 Огибающая геодезических
- 1.5 Геодезический многоугольник
- 1.6 Решение прямой и обратной задач
2 Геодезические на трехосном эллипсоиде
- 2.1 Трехосная система координат
- 2.2 Решение Якоби
- 2.3 Съемка трехосных геодезических
3 Приложения
4 См. Также
5 Примечания
6 Ссылки
7 Внешние ссылки

Геодезические на эллипсоиде вращения

Есть несколько способов определения геодезических (Hilbert Cohn-Vossen 1952, стр. 220–221). Простое определение - это кратчайший путь между двумя точками на поверхности. Однако часто бывает более полезно определить их как пути с нулевой геодезической кривизной - т.е. аналог прямых линий на искривленной поверхности. Эти определения, перемещаются по поверхности эллипсоида так далеко, что они начинают возвращаться к начальной точке, так что маршруты проходят через новые пути, которые пересекаются или пересекаются заново. Достаточно короткие сегменты по-прежнему являются кратчайшим путем между их конечными точками, но геодезические не обязательно являются минимальными в глобальном масштабе (то есть самыми короткими среди всех путей). Каждый кратчайший в мире путь является геодезическим, но не наоборот.

К концу 18 века эллипсоид вращения (также используется термин сфероид ) был общепринятым приближением к фигуре Земли. Регулировка триангуляции сетей влечет за собой уменьшение всех измерений к эллипсоид и решая полученную двухмерную задачу в качестве упражнений в сфероидальной тригономет (Bomford тысяча девятьсот пятьдесят два, Глава 3) (Лейк и др. 2015, §4.5).

Рис. 1. Геодезическая AB на эллипсоиде вращения. N - северный полюс, а EFH лежат на экваторе.

Можно свести различные геодезические задачи к одному из двух типов. Рассмотрим две точки: A на широте φ1и долготе λ1и B на широте φ 2 и долготе λ 2 (см. Рис. 1). Соединяющая геодезическая (от A до B) представляет собой AB длиной s 12, которая имеет азимуты α1и α 2 на двух конечных точках. Обычно две геодезические задачи:

прямая геодезическая задача или первая геодезическая задача, заданная A, α 1 и s 12, определить B и α 2;
обратная геодезическая задача или вторая геодезическая задача, заданные A и B, определяют s 12, α 1 и α 2.

Как видно из рис. 1, эти задачи включают решение треугольник NAB с одним углом, α 1 для задач и λ 12 = λ 2 - λ 1 для обратной задачи, и его двух дополнительных сторон. Для решения этих задач являются простые упражнения в сферической тригонометрии, решение которой дается , решение для решения сферического треугольника. (См. Статью о навигации по большому кругу.)

Для эллипсоида характерная постоянная, определяющая геодезическую, была найдена Клеро (1735). Систематическое решение для путей геодезических было дано Лежандром (1806) и Ориани (1806) (и последующими статьями в 1808 и 1810). Полное решение прямые задачи (вместе с вычислительными таблицами и разработанным примером) дает Бессель (1825 г.).

В 18 веке геодезические обычно назывались «кратчайшими линиями». Термин «геодезическая линия» был введен Лапласом (1799b) :

Nous désignerons cette ligne sous le nom de ligne géodésique [Мы будем называть эту линию геодезической линией].

Эта терминология была введена в английский язык как «геодезическая линия» или как «геодезическая линия», например (Hutton 1811),

Линия, приведенная так, как мы сейчас проведем, или выведенная из тригонометрические меры указанными средствами или средствами, называется геодезической геодезической линией: она имеет свойство быть самой короткой, которую можно провести между ее концами на поверхности Земли; и, следовательно, это правильная маршрутная мера расстояния между двумя точками.

В других областях предпочтение было отдано геодезической линии, часто используемой до геодезической.

В этом разделе рассматривается проблема эллипсоида вращения (как сжатого, так и вытянутого). Задача о трехосном эллипсоиде в следующем разделе.

Уравнения геодезической

Рис. 2. Дифференциальный элемент меридионального эллипса.

Рис. 3. Дифференциальный элемент геодезической на эллипсоиде.

Здесь развиты уравнения для геодезической; вывод полностью соответствует выводу Бесселя (1825). Джордан и Эггерт (1941), Багратуни (1962, §15), Ганьшин (1967, глава 5), Краковски и Томсон (1974, §4), Рапп (1993, §1.2), Джекели (2012) и Borre Strang (2012) также предоставил вывод эти уравнения.

Рассмотрим эллипсоид вращения с экваториальным радиусом a и полярной полуосью b. Определите уплощение f = (a - b) / a, эксцентриситет e = √a - b / a = √f (2 - f) и второй эксцентриситет e ′ = √a - b / b = e / (1 - е). (В большинстве приложений в геодезии эллипсоид считается считым, a>b; однако теория без изменений к вытянутым эллипсоидам, a < b, in which case f, e, and e′ are negative.)

Пусть элементарный сегмент пути на эллипсоиде имеет длину ds. Из рис. 2 и 3, мы видим, что если его азимут равенство α, то есть ds связан с dφ и dλ использованием

(1)

. Cos ⁡ α ds = ρ d φ = - d R sin ⁡ φ, sin ⁡ α ds знак равно р d λ, {\ displaystyle {\ color {white}.} \ Qquad \ cos \ alpha \, ds = \ rho \, d \ varphi = - {\ frac {dR} {\ sin \ varphi}}, \ quad \ sin \ alpha \, ds = R \, d \ lambda,}

{\ displaystyle {\ color {white}.} \ qquad \ cos \ alpha \, ds = \ rho \, d \ varphi = - {\ frac {dR} {\ sin \ varphi}}, \ quad \ sin \ alpha \, ds = R \, d \ lambda,}

где ρ - меридиональный радиус кривизны, R = ν cosφ - радиус окружности широты φ, а ν - нормальный радиус кривизны Таким образом. образом, элементарный сегмент задается как

ds 2 = ρ 2 d φ 2 + R 2 d λ 2 {\ displaystyle ds ^ {2} = \ rho ^ {2} \, d \ varphi ^ {2} + R ^ {2} \, d \ lambda ^ {2}}

{\ displaystyle ds ^ {2} = \ rho ^ {2} \, d \ varphi ^ {2} + R ^ {2} \, d \ lambda ^ {2}}

или

ds = ρ 2 φ ′ 2 + R 2 d λ ≡ L (φ, φ ') d λ, {\ Displaystyle {\ begin { align} ds = {\ sqrt {\ rho ^ {2} \ varphi '^ {2} + R ^ { 2}}} \, d \ лямбда \\ \ эквив L (\ varp hi, \ varphi ') \, d \ lambda, \ end {align}}}

{\begin{aligned}ds={\sqrt {\rho ^{2}\varphi '^{2}+R^{2}}}\,d\lambda \\\equiv L(\varphi,\varphi ')\,d\lambda,\end{aligned}}

где φ ′ = dφ / dλ и функция Лагранжа L зависит от φ через ρ (φ) и R (φ). Длина произвольного пути между (φ 1, λ 1) и (φ 2, λ 2) определяется как

s 12 знак равно ∫ λ 1 λ 2 L (φ, φ ') d λ, {\ displaystyle s_ {12} = \ int _ {\ lambda _ {1}} ^ {\ lambda _ {2}} L (\ varphi, \ varphi ') \, d \ lambda,}

s_{12}=\int _{\lambda _{1}}^{\lambda _{2}}L(\varphi,\varphi ')\,d\lambda,

где φ - функция от λ, удовлетворяющая φ (λ 1) = φ 1 и φ (λ 2) = φ 2. Кратчайший путь или геодезическая влечет за собой нахождение той функции φ (λ), которая минимизирует s 12. Это упражнение в вариационном исчислении, условие минимизации задается тождеством Бельтрами,

L - φ ′ ∂ L ∂ φ ′ = const. {\ displaystyle L- \ varphi '{\ frac {\ partial L} {\ partial \ varphi'}} = {\ text {const.}}}

L-\varphi '{\frac {\partial L}{\partial \varphi '}}={\text{const.}}

Подставив L и используя уравнения (1) дает

R sin ⁡ α = const. {\ displaystyle R \ sin \ alpha = {\ text {const.}}}

R \ sin \ alpha = \ text {const.}

Клеро (1735) нашел это отношение, используя геометрическую конструкцию; аналогичный вывод представлен Люстерником (1964, §10). Дифференциация этого отношения дает

d α = sin ⁡ φ d λ. {\ displaystyle d \ alpha = \ sin \ varphi \, d \ lambda.}

{\ displaystyle d \ alpha = \ sin \ varphi \, d \ lambda.}

Это вместе с уравнениями. (1) приводит к системе обыкновенные дифференциальных уравнений для геодезической

. d φ d s = cos ⁡ α ρ; d λ d s = sin ⁡ α ν cos ⁡ φ; d α d s = tan ⁡ φ sin ⁡ α ν. {\ displaystyle {\ color {white}.} \ qquad {\ frac {d \ varphi} {ds}} = {\ frac {\ cos \ alpha} {\ rho}}; \ quad {\ frac {d \ lambda} {ds}} = {\ frac {\ sin \ alpha} {\ nu \ cos \ varphi}}; \ quad {\ frac {d \ alpha} {ds}} = {\ frac {\ tan \ varphi \ sin \ alpha} {\ nu}}.}

{\ displaystyle {\ color {white}.} \ qquad {\ frac {d \ varphi} { ds}} = {\ frac {\ cos \ alpha} {\ rho}}; \ quad {\ frac {d \ lambda} {ds}} = {\ frac {\ sin \ alpha} {\ nu \ cos \ varphi}}; \ quad {\ frac {d \ alpha} {ds}} = {\ frac {\ tan \ varphi \ sin \ alpha} {\ nu}}.}

Мы можем выразить R через параметрическую широту, β, используя

R = a cos ⁡ β, {\ displaystyle R = a \ cos \ beta,}

{\ displaystyle R = a \ cos \ beta,}

и соотношение Клеро становится

sin ⁡ α 1 cos ⁡ β 1 = sin ⁡ α 2 соз ⁡ β 2. {\ displaystyle \ sin \ alpha _ {1} \ cos \ beta _ {1} = \ sin \ alpha _ {2} \ cos \ beta _ {2}.}

\ sin \ alpha_1 \ cos \ beta_1 = \ sin \ альфа_2 \ соз \ бета_2.

Рис. 4. Геодезическая задача на вспомогательной сфере.

Рис. 5. Элементарная геодезическая задача на вспомогательной сфере.

Это правило синуса сферической тригонометрии, связывающее две стороны треугольника NAB (см. Рис. 4), NA = ⁄ 2 π - β 1, и NB = ⁄ 2 π - β 2 и их противоположные углы B = π - α 2 и A = α 1.

Чтобы найти соотношение для третьей стороны AB = σ 12, длина сферической дуги и включенного угла N = ω 12, сферическая долгота, рассмотреть полезно треугольник NEP, представляющий геодезическую, начинающуюся на экваторе; см. рис. 5. На этом рисунке переменные, соответствующие к вспомогательной сфере, показаны с величинами для эллипсоида, показанными в скобках. Величины без индексов к произвольной точке P; E, точка, в которой используется геодезическая пересечение экватор в северном направлении, используется как начало координат для σ, s и ω.

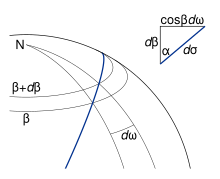Рис. 6. Дифференциальный элемент геодезической на сфере.

Если удлинить сторону EP бесконечно малого перемещения P (см. Рис. 6), получим

(2)

. cos ⁡ α d σ = d β, sin ⁡ α d σ = cos ⁡ β d ω. {\ displaystyle {\ color {white}.} \ qquad \ cos \ alpha \, d \ sigma = d \ beta, \ quad \ sin \ alpha \, d \ sigma = \ cos \ beta \, d \ omega.}

{\ color {white}.} \ Qquad \ cos \ alpha \, d \ sigma = d \ beta, \ quad \ грех \ альфа \, д \ сигма = \ соз \ бета \, д \ омега.

Объединение соотношений. (1) и (2) дают дифференциальные уравнения для s и λ

1 a d s d σ = d λ d ω = sin ⁡ β sin ⁡ φ. {\ displaystyle {\ frac {1} {a}} {\ frac {ds} {d \ sigma}} = {\ frac {d \ lambda} {d \ omega}} = {\ frac {\ sin \ beta} {\ sin \ varphi}}.}

{ \ displaystyle {\ frac {1} {a}} {\ frac {ds} {d \ sigma}} = {\ frac {d \ lambda} {d \ omega}} = {\ frac {\ sin \ beta} { \ sin \ varphi}}.}

Соотношение между β и φ составляет

tan ⁡ β = 1 - e 2 tan ⁡ φ = (1 - f) tan ⁡ φ, {\ displaystyle \ tan \ beta = {\ sqrt {1-e ^ {2}}} \ tan \ varphi = (1-f) \ tan \ varphi,}

{\ displaystyle \ tan \ beta = {\ sqrt {1-e ^ {2}}} \ tan \ varphi = (1-f) \ tan \ varphi,}

, что дает

sin ⁡ β sin ⁡ φ = 1 - e 2 cos 2 ⁡ β, {\ displaystyle {\ frac {\ sin \ beta} {\ sin \ varphi}} = {\ sqrt {1-e ^ {2} \ cos ^ {2} \ beta}},}

{\ displaystyle {\ frac {\ sin \ beta} {\ sin \ varphi}} = {\ sqrt {1-e ^ {2} \ cos ^ {2} \ beta}},}

так что дифференциальные уравнения имеют геодезической вид

1 adsd σ = d λ d ω = 1 - e 2 cos 2 ⁡ β. {\ displaystyle {\ frac {1} {a}} {\ frac {ds} {d \ sigma}} = {\ frac {d \ lambda} {d \ omega}} = {\ sqrt {1-e ^ { 2} \ cos ^ {2} \ beta}}.}

\ frac1a \ frac {ds} {d \ sigma} = \ frac {d \ lambda } {d \ omega} = \ sqrt {1-e ^ 2 \ cos ^ 2 \ beta}.

Последний шаг - использовать σ в качестве независимого уравнения в обоих этих дифференциальных уравнениях и тем самым выразить s и λ как интегралы. Применение правил синуса к вершинам E и G сферического треугольника EGP на рис. 5 дает

грех ⁡ β знак равно грех ⁡ β (σ; α 0) = соз ⁡ α 0 грех ⁡ σ, {\ displaystyle \ sin \ beta = \ sin \ beta (\ sigma; \ alpha _ {0}) = \ cos \ alpha _ {0} \ sin \ sigma,}

\ грех \ бета = \ грех \ бета (\ сигма; \ альфа_0) = \ соз \ альфа_0 \ грех \ сигма,

где α 0 - азимут в точке E Подставляя это в уравнение для ds / dσ и интегрируя результат, получаем

(3)

. sb знак равно ∫ 0 σ 1 + К 2 грех 2 ⁡ σ ′ d σ ′, {\ displaystyle {\ color {white}.} \ qquad {\ frac {s} {b}} = \ int _ {0} ^ {\ sigma} {\ sqrt {1 + k ^ {2} \ sin ^ {2} \ sigma '}} \, d \ sigma',}

{\color {white}.}\qquad {\frac {s}{b}}=\int _{0}^{\sigma }{\sqrt {1+k^{2}\sin ^{2}\sigma '}}\,d\sigma ',

где

k = e ′ cos ⁡ α 0, {\ displaystyle k = e '\ cos \ alpha _ {0},}

k = e'\cos\alpha_0,

и пределы интеграла выбраны так, чтобы s (σ = 0) = 0. Лежандр (1811, стр. 180) укажите, что уравнение для s такое же, как уравнение для дуги на эллипсе с полуосями b√1 + e ′ cosα 0 и b. Чтобы выразить уравнение для λ через σ, запишем

d ω = sin ⁡ α 0 cos 2 ⁡ β d σ, {\ displaystyle d \ omega = {\ frac {\ sin \ alpha _ {0}} {\ cos ^ {2} \ beta}} \, d \ sigma,}

d \ omega = \ frac {\ sin \ alpha_0} {\ cos ^ 2 \ beta} \, d \ sigma,

что следует из уравнений. (2) и соотношение Клеро. Это дает

(4)

. λ - λ 0 знак равно ω - е грех ⁡ α 0 ∫ 0 σ 2 - f 1 + (1 - f) 1 + k 2 sin 2 ⁡ σ ′ d σ ′, {\ displaystyle {\ color {white}.}. \ qquad \ lambda - \ lambda _ {0} = \ omega -f \ sin \ alpha _ {0} \ int _ {0} ^ {\ sigma} {\ frac {2-f} {1+ (1-f) {\ sqrt {1 + k ^ {2} \ sin ^ {2} \ sigma '}}} \, d \ sigma',}

{\color {white}.}\qquad \lambda -\lambda _{0}=\omega -f\sin \alpha _{0}\int _{0}^{\sigma }{\frac {2-f}{1+(1-f){\sqrt {1+k^{2}\sin ^{2}\sigma '}}}}\,d\sigma ',

и пределы интегралов выбраны так, чтобы λ = λ 0 на пересечение экватора, σ = 0.

Это завершает решение пути геодезической с использованием сферы. С помощью этого устройства большой круг может быть точно сопоставлен с геодезической на эллипсоиде вращения.

Существует также несколько способов аппроксимации геодезических на земном эллипсоиде (с небольшим уплощением) (Rapp 1991, §6); некоторые из них в статье о географическом расстоянии. Однако они обычно сравнимы по сложности с методом точного решения (Jekeli 2012, §2.1.4).

Поведение геодезических

Рис. 7. Меридианы и экватор - единственные замкнутые геодезические. (Для сильно уплощенных эллипсоидов существуют другие замкнутые геодезические; см. Рис. 11 и 12). Геодезические на сплющенном эллипсоиде (f = ⁄ 50) с α 0 = 45 °.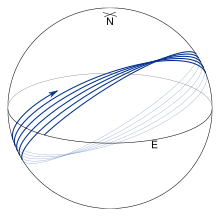

Рис. 8. По геодезической на эллипсоиде около 5 витков.

Рис. 9. Та же геодезическая примерно после 70 обходов.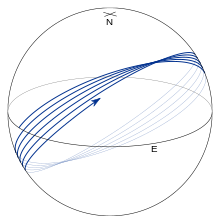

Рис. 10. Геодезическая на вытянутом эллипсоиде (f = - ⁄ 50) с α 0 = 45 °. Соответствующий с рис. 8.

Рис. 7 показаны простые замкнутые геодезические, состоящие из меридианов (зеленый) и экватора (красный). (Здесь определение «простой» означает, что геодезическая замыкается на себе без промежуточного самопересечения.) Это следует из правил для геодезических, приведенных в предыдущем разделе.

Все остальные геодезические представлены на рис. 8 и 9, начинающаяся геодезическая, начинающаяся на экваторе с α 0 = 45 °. Геодезическая колеблется вокруг экватора. Экваториальные пересечения называются узлами, а точки максимальной или минимальной широты - вершинами; параметрические широты вершин равны β = ± (⁄ 2 π - | α 0 |). Геодезическая совершает одно полное колебание по широте, чем долгота увеличится на 360 °. Таким образом, при каждом последующем пересечении экватора в северном направлении (см. Рис. 8) λ меньше полного оборота экватора примерно на 2π f sinα 0 (для вытянутого эллипсоида эта величина отрицательна и λ совершает больше, чем полный цикл, см. рис. 10). Почти для всех значений α 0 геодезическая заполнит ту часть эллипсоида между двумя широтами вершин (см. Рис. 9).

Две дополнительные замкнутые геодезические нагрузки для сжатого эллипсоида, ⁄ a = ⁄ 7.

Рис. 11. Вид сбоку.

Рис. 12. Вид сверху.

Если эллипсоид заблокирует, то есть ⁄ a< ⁄2, возможен другой класс простых замкнутых геодезических (Клингенберг 1982, §3.5.19). Две такие геодезические показаны на рис. 11 и 12. Здесь ⁄ a = ⁄ 7 и экваториальный азимут, α 0, для зеленой (соответственно синей) геодезической выбранной так, чтобы быть 53,175 ° ( соответственно 75,192 °), так что геодезическая совершает 2 (соответственно 3) полных колебания вокруг экватора на одном витке эллипсоида.

Рис. 13. Геодезические (синий) из одной точки для f = ⁄ 10, φ 1 = −30 °; геодезические круги показаны зеленым цветом, геометрическое место разреза - красным.

Рис. 13 показаны геодезические (синим цветом), исходящие из A с α 1, кратным 15 °, до точки, в которой они перестают быть кратчайшими путями. (Уплощение было увеличено до ⁄ 10, чтобы подчеркнуть эллипсоидальные эффекты.) Также проявились (зеленым цветом) кривые константы s 12, которые дополняют собой геодезические круги с центром А. Гаусс (1828) показано, что на любой поверхности геодезические и геодезическая окружность пересекаются под прямым углом. Красная линия - это геометрическое место разреза, геометрические точки, которые имеют несколько кратчайших геодезических из A. На сфере геометрическое место является точкой. На сплюснутом эллипсоиде (показанном здесь) это сегмент окружности широты с центром в точке , противоположной точке A, φ = −φ 1. Продольная протяженность геометрического места разреза равна λ 12 ∈ [π - f π cosφ 1, π + f π cosφ 1 ]. Если A лежит на экваторе, φ 1 = 0, это соотношение является точным, и, как следствие, экватор является кратчайшей геодезической, только если | λ 12 | ≤ (1 - е) π. Для вытянутого эллипсоида геометрическое место разреза - это сегмент антимеридиана с точкой в точке, противоположной точке A, λ 12 = π, и это означает, что меридиональные геодезические перестают быть кратчайшими путями до того, как точка противоположности будет достигнута.

Дифференциальные свойства геодезических

Различные задачи, связанные с геодезическими, требуют знания их поведения при возмущении. Это полезно при тригонометрической корректировке (Ehlert 1993), физических свойств сигналов, следующих за геодезическими, и т. Д. Рассмотрим опорную геодезическую, параметры, и вторую геодезическую на небольшом расстоянии t от него. Гаусс (1828) показал, что t (s) подчиняется уравнению Гаусса-Якоби

. d 2 t (s) ds 2 знак равно К (s) t (s), {\ displaystyle {\ color {white}.} \ qquad \ displaystyle {\ frac {d ^ {2} t (s)} {ds ^ {2}}} = K (s) t (s),}

{\ color {white}.} \ qquad \ displaystyle \ frac { d ^ 2t (s)} {ds ^ 2} = K (s) t (s),

Рис. 14. Определение приведенной длины и геодезического масштаба.

где K (s) - гауссова кривизна в точке s. Как линейное однородное дифференциальное уравнение второго порядка, его решение может быть выражено как сумма двух независимых решений

t (s 2) = C m (s 1, s 2) + DM (s 1, s 2) {\ displaystyle t ( s_ {2}) = Cm (s_ {1}, s_ {2}) + DM (s_ {1}, s_ {2})}

t (s_2) = C m (s_1, s_2) + DM (s_1, s_2)

где

m (s 1, s 1) = 0, dm (s 1, s 2) ds 2 | s 2 = s 1 = 1, M (s 1, s 1) = 1, d M (s 1, s 2) d s 2 | s 2 знак равно s 1 знак равно 0. {\ displaystyle {\ begin {align} m (s_ {1}, s_ {1}) = 0, \ quad \ left. {\ frac {dm (s_ {1}, s_) {2})} {ds_ {2}}} \ right | _ {s_ {2} = s_ {1}} = 1, \\ M (s_ {1}, s_ {1}) = 1, \ quad \ left. {\ frac {dM (s_ {1}, s_ {2})} {ds_ {2}}} \ right | _ {s_ {2} = s_ {1}} = 0. \ end {выровнено}}}

{\ displaystyle {\ begin {align} m (s_ {1}, s_ {1}) = 0, \ quad \ left. {\ frac {dm (s_ {1}, s_ {2})} {ds_ {2}}} \ right | _ {s_ {2} = s_ {1}} = 1, \\ M (s_ {1}, s_ {1}) = 1, \ quad \ left. {\ Frac {dM (s_ {1}, s_ {2})} {ds_ {2}}} \ right | _ {s_ {2} = s_ {1}} = 0. \ end {align}}}

Величина m (s 1, s 2) = m 12 - это так называемая уменьшенная длина, а M (s 1, s 2) = M 12 - геодезическая шкала. Их основные определения показаны на рис. 14.

Гауссова кривизна для эллипсоида вращения равна

K = 1 ρ ν = (1 - e 2 sin 2 ⁡ φ) 2 б 2 знак равно б 2 а 4 (1 - е 2 соз 2 ⁡ β) 2. {\ displaystyle K = {\ frac {1} {\ rho \ nu}} = {\ frac {{\ bigl (} 1-e ^ {2} \ sin ^ {2} \ varphi {\ bigr)} ^ { 2}} {b ^ {2}}} = {\ frac {b ^ {2}} {a ^ {4} {\ bigl ( } 1-e ^ {2} \ cos ^ {2} \ beta {\ bigr)} ^ {2}}}.}

{\ displaystyle K = {\ frac {1} {\ rho \ nu}} = {\ frac {{\ bigl (} 1-e ^ {2} \ sin ^ { 2} \ varphi {\ bigr)} ^ {2}} {b ^ {2}}} = {\ frac {b ^ {2}} {a ^ {4} {\ bigl (} 1-e ^ {2 } \ cos ^ {2} \ beta {\ bigr)} ^ {2}}}.}

Хельмерт (1880, уравнение (6.5.1.)) Решил уравнение Гаусса -Якоби для этого случая, допуская m 12 и M 12 для выражения в виде интегралов.

Как видно из рис. 14 (верхний подфигура), разделение двух геодезических, начинающихся в одной точке с азимутами, различающихся на dα 1, составляет m 12dα1. На замкнутой поверхности, такой как эллипсоид, м 12 колеблется около нуля. Точка, в которой m 12 становится равной нулю, является точкой , сопряженной с начальной точкой. Чтобы геодезическая между A и краткой длиной s 12 былачайшим путем, она должна удовлетворять условию Якоби (Jacobi 1837) (Jacobi 1866, §6) (Forsyth 1927, §§26–27) (Bliss 1916), что нет точки, сопряженной с A между A и B. Если это условие не выполнено, то есть ближайший путь (не обязательно геодезический), который короче. Таким образом, условие Якоби является локальным свойством геодезическим и является ограниченным условием того, что геодезическая является кратчайшим глобальным путем. Необходимые и достаточные условия для того, чтобы геодезическая была кратчайшим путем:

для сжатого эллипсоида, | σ 12 | ≤ π;
для вытянутого эллипсоида, | λ 12 | ≤ π, если α 0 ≠ 0; если α 0 = 0, требуется дополнительное условие m 12 ≥ 0, если | λ 12 | = π.

Огибающая геодезических

Геодезические из одной точки (f = ⁄ 10, φ 1 = −30 °)

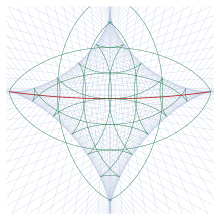Рис. 15. Огибающая геодезических из точек A при φ 1 = −30 °.

Рис. 16. Четыре геодезические, соединяющие точку A и точку B, φ 2 = 26 °, λ 12 = 175 °.

Геодезические из конкретной точки A, если продолжить Геодезические точки, для которых α 1 кратно 3 °, показаны голубым цветом. (Геодезические показаны только для первого их прохождения рядом с противоположной точкой, а не для будущего.) Некоторые геодезические круги показаны зеленым; они образуют бугорки на конверте. Место разреза показано красным. Огибающая - это сопряженное место точек, сопряженных с A; точки на конверте могут быть вычислены путем нахождения точки, в которой m 12 = 0 на геодезической. Якоби (1891) называет эту звездообразную фигуру, созданную оболочку, астроидом.

Вне астроиды две геодезические пересекаются в каждой точке; таким образом, между двумя точками находятся геодезические (длиной примерно половину окружности эллипсоида). Это соответствует ситуации на сфере, где есть «короткий» и «длинный» маршруты на большом круге между двумя точками. Внутри астроиды в каждой точке пересекаются четыре геодезические. Четыре таких геодезических показаны на рис. 16, где геодезические пронумерованы в порядке возрастания длины. (На этом рисунке используется то же положение для A, что и на рисунке 13, и оно нарисовано в той же проекции.) Две более короткие геодезические устойчивые, то есть m 12>0, так что нет ближайшего пути, соединяющего две точки короче; два других нестабильны. Только самая короткая линия (первая) имеет σ 12 ≤ π. Все геодезические касаются оболочки, которая на рисунке зеленым цветом.

Астроида - это (внешняя) эволюция геодезических окружений с центром A. Аналогично, геодезические окружения являются эвольвентами астроиды.

Площадь геодезического многоугольника

Геодезический многоугольник - это многоугольник, стороны которого являются геодезическими. Это аналог сферического многоугольника, стороны которого отличаются большие окружности. Площадь такого многоугольника может быть найдена, сначала вычислить площадь между геодезическим сегментом и экватором, то есть площадь четырехугольника AFHB на рисунке 1 (Danielsen 1989). Как только эта площадь известна, площадь многоугольника может быть вычислена суммирования вкладов всех краев многоугольника.

Здесь выражение для площади S 12 AFHB разработано в соответствии с Sjöberg (2006). Площадь любой замкнутой области эллипсоида равна

T = ∫ d T = ∫ 1 K cos ⁡ φ d φ d λ, {\ displaystyle T = \ int dT = \ int {\ frac {1} {K}} \ cos \ varphi \, d \ varphi \, d \ lambda,}

{\ displaystyle T = \ int dT = \ int {\ frac {1} {K }} \ cos \ varphi \, d \ varphi \, d \ lambda,}

где dT - это элемент площади поверхности, а K - гауссова кривизна. Теперь теорема Гаусса - Бонне применяется к состояниям геодезического многоугольника

Γ = ∫ K d T = ∫ cos ⁡ φ d φ d λ, {\ displaystyle \ Gamma = \ int K \, dT = \ int \ соз \ varphi \, d \ varphi \, d \ lambda,}

{\ displaystyle \ Gamma = \ int K \, dT = \ int \ cos \ varphi \, d \ varphi \, d \ lambda,}

где

Γ = 2 π - ∑ j θ j {\ displaystyle \ Gamma = 2 \ pi - \ sum _ {j} \ theta _ {j}}

\ Гамма = 2 \ pi - \ sum_j \ theta_j

- геодезический эксцесс, а θ j - внешний угол в вершине j. Умножение этого уравнения для Γ на R 2, где R 2 - это автономный радиус, и вычитание из уравнений для T дает

T = R 2 2 Γ + ∫ (1 K - R 2 2) cos ⁡ φ d φ d λ = R 2 2 Γ + ∫ (b 2 (1 - e 2 sin 2 ⁡ φ) 2 - R 2 2) cos ⁡ φ d φ d λ, {\ displaystyle {\ begin {align} T = R_ {2} ^ {2} \, \ Gamma + \ int {\ biggl (} {\ frac {1} {K}} - R_ {2} ^ {2} {\ biggr)} \ cos \ varphi \, d \ varphi \, d \ lambda \\ = R_ {2} ^ {2} \, \ Gamma + \ int {\ Biggl (} {\ frac { б ^ {2}} {{\ bigl (} 1-е ^ {2} \ sin ^ {2} \ varphi {\ bigr)} ^ {2}}} - R_ {2} ^ {2} {\ Biggr)} \ cos \ varphi \, d \ varphi \, d \ lambda, \ end {align}}}

{\ displaystyle {\ begin {выровнено} T = R_ {2} ^ {2} \, \ Gamma + \ int {\ biggl (} {\ frac {1 } {K}} - R_ {2} ^ {2} {\ biggr)} \ cos \ varphi \, d \ varphi \, d \ lambda \\ = R_ {2} ^ {2} \, \ Gamma + \ int {\ Biggl (} {\ frac {b ^ {2}} {{\ bigl (} 1-e ^ {2} \ sin ^ {2} \ varphi {\ bigr)} ^ {2}}} - R_ {2} ^ {2} {\ Biggr)} \ cos \ varphi \, d \ varphi \, d \ lambda, \ end {align}}}

, где было заменено значение K для эллипсоида. Применяя эту формулу к четырехугольнику AFHB, отмечая, что Γ = α 2 - α 1, и выполняя интеграл по φ, получаем

S 12 = R 2 2 (α 2 - α 1) + b 2 ∫ λ 1 λ 2 (1 2 (1 - e 2 sin 2 ⁡ φ) + tanh - 1 ⁡ (e sin ⁡ φ) 2 e sin ⁡ φ - R 2 2 b 2) sin ⁡ φ d λ, {\ Displaystyle S_ {12} = R_ {2} ^ {2} (\ alpha _ {2} - \ alpha _ {1}) + b ^ {2} \ int _ {\ lambda _ {1} } ^ {\ lambda _ {2}} {\ biggl (} {\ frac {1} {2 {\ bigl (} 1-e ^ {2} \ sin ^ {2} \ varphi {\ bigr)}}} + {\ frac {\ tanh ^ {- 1} (e \ sin \ varphi)} {2e \ sin \ varphi}} - {\ frac {R_ {2} ^ {2}} {b ^ {2}}} {\ biggr)} \ sin \ varphi \, d \ lambda,}

{\ displaystyle S_ {12} = R_ {2} ^ {2} (\ alpha _ {2} - \ alpha _ {1}) + b ^ {2} \ int _ {\ lambda _ {1}} ^ {\ lambda _ {2}} {\ biggl (} {\ frac {1} {2 {\ bigl (} 1-e ^ {2} \ sin ^ {2} \ varphi {\ bigr)}}} + {\ frac {\ tanh ^ {- 1} (e \ sin \ varphi)} {2e \ sin \ varphi}} - {\ frac {R_ {2} ^ {2}} {b ^ {2}}} {\ biggr)} \ sin \ varphi \, d \ lambda,}

где интеграл берется по геодезической прямой (так что φ неявно является функцией λ). Интеграл может быть выражен как ряд, действительный для малых f (Danielsen 1989) (Karney 2013, §6 и добавление).

Площадь геодезического многоугольника определяется суммированием S 12 по его краям. Этот результат верен при условии, что многоугольник не содержит полюса; если это так, к сумме необходимо добавить 2π R 2. Если ребра заданы своими вершинами, то удобное выражение для геодезического избытка E 12 = α 2 - α 1 будет

tan ⁡ E 12 2 знак равно грех ⁡ 1 2 (β 2 + β 1) соз ⁡ 1 2 (β 2 - β 1) загар ⁡ ω 12 2. {\ displaystyle \ tan {\ frac {E_ {12}} {2}} = {\ frac {\ sin {\ tfrac {1} {2}} (\ beta _ {2} + \ beta _ {1})} {\ cos {\ tfrac {1} {2}} (\ beta _ {2} - \ beta _ {1})}} \ tan {\ frac {\ omega _ {12}} {2}}.}

\ tan \ frac {E_ {12}} 2 = \ frac {\ sin \ tfrac12 (\ beta_2 + \ beta_1)} {\ cos \ tfrac12 (\ beta_2 - \ beta_1)} \ tan \ frac {\ omega_ { 12}} 2.

Решение прямого и обратного задач

Решение геодезических задач влечет за собой отображение геодезической на вспомогательную сферу и решение задачи в навигации по большому кругу. При решении «элементарного» сферического треугольника для NEP на рис. 5 можно использовать правила Напье для квадрантных треугольников,

sin ⁡ α 0 = sin ⁡ α cos ⁡ β = tan ⁡ ω cot ⁡ σ, cos ⁡ σ = cos ⁡ β cos ⁡ ω = tan ⁡ α 0 детская кроватка ⁡ α, cos ⁡ α = cos ⁡ ω cos ⁡ α 0 = детская кроватка ⁡ σ tan ⁡ β, sin ⁡ β = cos ⁡ α 0 sin ⁡ σ = детская кроватка ⁡ α tan ⁡ ω, sin ⁡ ω = sin ⁡ σ грех ⁡ α знак равно загар ⁡ β загар ⁡ α 0. {\ Displaystyle {\ begin {align} \ sin \ alpha _ {0} = \ sin \ alpha \ cos \ beta = \ tan \ omega \ cot \ sigma, \\\ cos \ sigma = \ cos \ beta \ cos \ omega = \ tan \ alpha _ {0} \ cot \ alpha, \\\ cos \ alpha = \ cos \ omega \ cos \ alpha _ {0} = \ cot \ sigma \ tan \ beta, \\\ sin \ beta = \ cos \ alpha _ {0} \ sin \ sigma = \ cot \ alpha \ tan \ omega, \\\ sin \ omega = \ sin \ sigma \ sin \ alpha = \ tan \ beta \ tan \ alpha _ {0}. \ end {align}}}

{\ displaystyle {\ begin {align} \ sin \ alpha _ {0} = \ sin \ alpha \ cos \ beta = \ tan \ omega \ cot \ sigma, \\\ cos \ sigma = \ cos \ beta \ cos \ omega = \ tan \ alpha _ {0} \ cot \ alpha, \\\ cos \ альфа = \ cos \ omega \ cos \ alpha _ {0} = \ cot \ sigma \ tan \ beta, \\\ sin \ beta = \ cos \ alpha _ {0} \ sin \ sigma = \ cot \ alpha \ tan \ omega, \\\ грех \ омега = \ грех \ сигма \ гре х \ альфа = \ загар \ бета \ загар \ альфа _ {0}. \ конец {выравнивается}}}

Отображение геодезической вычисление интегралов для расстояний и долготы λ, уравнения. (3) и (4), и они зависят от параметров α 0.

Решение прямые задачи несложно, поскольку α 0 может быть определено непосредственно из заданных величин φ 1 и α 1.

В случае обратной задачи задано λ 12 ; это не может быть легко связано с эквивалентным сферическим углом ω 12, потому что α 0 неизвестно. Таким образом, решение проблемы требует, чтобы α 0 находился итеративно.

В геодезических приложениях, где мало, интегралы обычно вычисляются как ряды (Лежандр 1806) (Ориани 1806) (Бессель 1825) ( Хельмерт 1880) (Рейнсфорд 1955) (Рапп 1993). Для произвольного f интегралы (3) и (4) могут быть найдены с помощью числовой квадратуры или их выражения через эллиптические интегралы (Legendre 1806) (Cayley 1870).

Винсенти (1975) предлагает решения прямых и обратных задач; они основаны на последовательном расширении, выполняемом третьим порядком при сплющивании, обеспечивают точность около 0,1 мм для эллипсоида WGS84 ; однако обратный метод не может сходиться почти для противоположных точек. Karney (2013) продолжает разложение до шестого порядка, которого для обеспечения полной точности точность точности точность для | f | ≤ ⁄ 50 и улучшает решение обратной задачи, так что оно сходится во всех случаях. Карни (2013, добавление) расширяет методы, используя эллиптические интегралы, которые могут быть выполнены к эллипсоидам с произвольным уплощением.

Геодезические на трехосном эллипсоиде

Решение геодезической задачи для эллипсоида вращения математической точки зрения относительно просто: из-за симметрии геодезические имеют константу движение, заданное создание Клеро, позволяющее свести проблема к квадратуре. К началу 19 века (благодаря работам Лежандра, Ориани, Бесселя и др.) Было полное понимание свойств геодезических на эллипсоиде вращения.

С другой стороны, геодезические на трехосном эллипсоиде (с тремя неравными осями) не имеют очевидной постоянной постоянной и таким образом, представляющие собой сложную нерешенную проблему в первой половине XIX века. В замечательной статье Якоби (1839) обнаружил постоянную движение, позволившую также свести эту проблему к квадратуре (Клингенберг 1982, §3.5).

Трехосная система координат

Рассмотрим эллипсоид, определенно

h = X 2 a 2 + Y 2 b 2 + Z 2 c 2 = 1, {\ displaystyle h = {\ frac {X ^ {2}} {a ^ {2}}} + {\ frac {Y ^ {2}} {b ^ {2}}} + {\ frac {Z ^ {2}} {c ^ {2 }}} = 1,}

h = \ frac {X ^ 2} {a ^ 2} + \ frac {Y ^ 2} {b ^ 2} + \ frac {Z ^ 2} {c ^ 2} = 1,

где (X, Y, Z) декартовы координаты с центром эллипсоиде и без ограничения общности, a ≥ b ≥ c>0. Якоби (1866, §§26–27) использовались эллипсоидальные широта и долгота (β, ω), динамики

рис. 17. Эллипсоидальные координаты.

X = a cos ⁡ ω a 2 - b 2 sin 2 ⁡ β - c 2 cos 2 ⁡ β a 2 - c 2, Y = b cos ⁡ β sin ⁡ ω, Z = с грех ⁡ β а 2 грех 2 ⁡ ω + б 2 соз 2 ⁡ ω - с 2 а 2 - с 2. {\ displaystyle {\ begin {align} X = a \ cos \ omega {\ frac {\ sqrt {a ^ {2} -b ^ {2} \ sin ^ {2} \ beta -c ^ {2} \ cos ^ {2} \ beta}} {\ sqrt {a ^ {2} -c ^ {2}}}}, \\ Y = b \ cos \ beta \ sin \ omega, \\ Z = c \ sin \ beta {\ frac {\ sqrt {a ^ {2} \ sin ^ {2} \ omega + b ^ {2} \ cos ^ {2} \ omega -c ^ {2}}} {\ sqrt {a ^ {2 } -c ^ {2}}}}. \ end {align}}}

\ begin {align} X = a \ cos \ omega \ frac {\ sqrt {a ^ 2 - b ^ 2 \ sin ^ 2 \ beta - c ^ 2 \ cos ^ 2 \ beta}} {\ sqrt {a ^ 2 - c ^ 2}}, \\ Y = b \ cos \ beta \ sin \ omega, \\ Z = c \ sin \ beta \ гидроразрыв {\ sqrt {a ^ 2 \ sin ^ 2 \ omega + b ^ 2 \ cos ^ 2 \ ome ga - c ^ 2}} {\ sqrt {a ^ 2 - c ^ 2}}. \ end {align}

В пределе b → a β становится параметрической широтой для сжатого эллипсоида, поэтому использование символа β согласуется с предыдущим разделы. Однако ω отличается от сферической долготы, определенной выше.

Линии сетки постоянных β (синим цветом) и ω (зеленым) показаны на рис. 17. Они составляют ортогональную система координат: линии сетки пересекаются под прямым углом. Основные секции эллипсоида, определяемые X = 0 и Z = 0, показаны красным. Третий главный участок, Y = 0, перекрывается линиями β = ± 90 ° и ω = 0 ° или ± 180 °. Эти линии встречаются в четырех точках шлангокабеля (две из которых видны на этом рисунке), где главные радиусы кривизны равны. Здесь и на других рисунках в этом разделе параметры эллипсоида a: b: c = 1,01: 1: 0,8, и он рассматривается в ортогональной проекции из точки выше φ = 40 °, λ = 30 °.

Линии сетки эллипсоидальных координат можно интерпретировать тремя разными способами:

Это «линии кривизны» на эллипсоиде: они параллельны направлениям главной кривизны (Monge 1796).
Они также являются пересечениями эллипсоида с конфокальными системами гиперболоидов одного и двух листов (Дюпен 1813, Часть 5 ).
Наконец, это геодезические эллипсы и гиперболы, определенные с помощью двух соседних точек омбилизации (Hilbert Cohn-Vossen 1952, p. 188). Например, линии константы β на рис. 17 могут быть созданы с помощью знакомой конструкции строки для эллипсы с концами веревки, прикрепленными к двум точкам пуповины.

Решение Якоби

Якоби показало, что уравнения геодезических, выраженные в эллипсоидальных координатах, разделимы. Вот как он рассказал о своем открытии своему другу и соседу Бесселю (Якоби 1839, Письмо Бесселю),

Позавчера я уменьшил к квадратуре задачи геодезических линий на эллипсоиде с тремя неравными осями. Это простейшие формулы в мире, абелевы интегралы, которые становятся хорошо известными эллиптическими интегралами, если две оси равны..

Кенигсберг, 28 декабря '38.

Решение, данное Якоби (Jacobi 1839) (Jacobi 1866, §28):

δ = ∫ b 2 sin 2 ⁡ β + c 2 cos 2 ⁡ β d β a 2 - b 2 sin 2 ⁡ β - c 2 cos 2 ⁡ β (b 2 - c 2) cos 2 ⁡ β - γ - ∫ a 2 sin 2 ⁡ ω + b 2 cos 2 ⁡ ω d ω a 2 sin 2 ⁡ ω + b 2 cos 2 ⁡ ω - c 2 (a 2 - b 2) sin 2 ⁡ ω + γ. {\ displaystyle {\ begin {align} \ delta = \ int {\ frac {{\ sqrt {b ^ {2} \ sin ^ {2} \ beta + c ^ {2} \ cos ^ {2} \ beta }} \, d \ beta} {{\ sqrt {a ^ {2} -b ^ {2} \ sin ^ {2} \ beta -c ^ {2} \ cos ^ {2} \ beta}} {\ sqrt {{\ bigl (} b ^ {2} -c ^ {2} {\ bigr)} \ cos ^ {2} \ beta - \ gamma}}}} \\ [6pt] \ quad - \ int { \ frac {{\ sqrt {a ^ {2} \ sin ^ {2} \ omega + b ^ {2} \ cos ^ {2} \ omega}} \, d \ omega} {{\ sqrt {a ^ { 2} \ sin ^ {2} \ omega + b ^ {2} \ cos ^ {2} \ omega -c ^ {2}}} {\ sqrt {{\ bigl (} a ^ {2} -b ^ { 2} {\ bigr)} \ sin ^ {2} \ omega + \ gamma}}}}. \ End {align}}}

{\ displaystyle {\ begin {align} \ delta = \ int {\ frac {{\ sqrt {b ^ {2} \ sin ^ {2} \ beta + c ^ {2} \ cos ^ {2} \ beta}} \, d \ beta} {{\ sqrt {a ^ {2} -b ^ {2} \ sin ^ {2} \ b eta -c ^ {2} \ cos ^ {2 } \ beta}} {\ sqrt {{\ bigl (} b ^ {2} -c ^ {2} {\ bigr)} \ cos ^ {2} \ beta - \ gamma}}} \\ [6pt] \ quad - \ int {\ frac {{\ sqrt {a ^ {2} \ sin ^ {2} \ omega + b ^ {2} \ cos ^ {2} \ omega}} \, d \ omega} { {\ sqrt {a ^ {2} \ sin ^ {2} \ omega + b ^ {2} \ cos ^ {2} \ omega -c ^ {2}}} {\ sqrt {{\ bigl (} a ^ {2} -b ^ {2} {\ bigr)} \ sin ^ {2} \ omega + \ gamma}}}}. \ end {align}}}

Как отмечает Якоби, «функция угла β равна функции угла ω.Эти две функции являются просто абелевыми интегралами... »Две константы δ и γ появляются в растворе. Обычно δ равно нулю, если нижние пределы интегралов принимаются за начальную точку геодезической, а направление геодезических определяется с помощью γ. Однако для геодезических, начинающихся в точках пуповины, γ = 0, а δ определяют направление в точке пуповины. Константа γ может быть выражена как

γ = (b 2 - c 2) cos 2 ⁡ β sin 2 ⁡ α - (a 2 - b 2) sin 2 ⁡ ω cos 2 ⁡ α, {\ displaystyle \ gamma = { \ bigl (} b ^ {2} -c ^ {2} {\ bigr)} \ cos ^ {2} \ beta \ sin ^ {2} \ alpha - {\ bigl (} a ^ {2} -b ^ {2} {\ bigl)} \ sin ^ {2} \ omega \ cos ^ {2} \ alpha,}

{\ displaystyle \ gamma = {\ bigl (} b ^ {2} -c ^ {2} {\ bigr)} \ cos ^ {2} \ beta \ sin ^ {2} \ alpha - {\ bigl (} a ^ {2} -b ^ {2} {\ bigl)} \ sin ^ {2} \ omega \ cos ^ {2} \ alpha,}

где α - угол, который геодезическая образует с линией постоянной ω. В пределе b → a это сводится к sinα cosβ = const., Известному введению Клеро. Вывод результата Якоби дается Дарбу (1894, §§583–584); он дает решение, найденное Лиувиллем (1846) для общих квадратичных поверхностей.

Съемка трехосных геодезических

Циркумполярных геодезических, ω 1 = 0 °, α 1 = 90 °.

Рис. 18. β 1 = 45,1 °.

Рис. 19. β 1 = 87,48 °.

На трехосном эллипсоиде есть только три простых замкнутых геодезических, три главных сечения эллипсоида, заданных формулами X = 0, Y = 0 и Z = 0. Для обзора других геодезических удобно рассматривать геодезические, которые пересекают главное сечение, Y = 0, под прямым углом. Такие геодезические показаны на рис. 18–22, в которых используются те же параметры эллипсоида и то же направление обзора, что и на рис. 17. Кроме того, три основных эллипса показаны на каждом из этих рисунков.

Если начальная точка β 1 ∈ (−90 °, 90 °), ω 1 = 0 и α 1 = 90 °, тогда γ>0 и геодезическая окружает эллипсоид в «циркумполярном» смысле. Геодезическая колеблется к северу и югу от экватора; при каждом колебании он совершает несколько менее полный оборот вокруг эллипсоида, что в типичном случае приводит к заполнению геодезической области, ограниченной двумя линиями широты β = ± β 1. Два примера на рис. 18 и 19. Рисунок 18 показывает практически то же поведение, что и сплющенного эллипсоида вращения (a ≈ b); сравните с рис. 9. Однако, если начальная точка находится на более высокой широте (рис. 18), наблюдающиеся в результате очевидны искажения. Все касательные к циркумполярной геодезической касаются конфок однополостного гиперболоида, который пересекает эллипсоид в точке β = β 1(Chasles 1846) (Hilbert Cohn-Vossen 1952, pp. 223–224).

Трансполярные геодезические, β 1 = 90 °, α 1 = 180 °.

Рис. 20. ω 1 = 39,9 °.

Фиг. 21. ω 1 = 9,966 °.

Если начальная точка β 1 = 90 °, ω 1 ∈ (0 °, 180 °), а α 1 = 180 °, тогда γ < 0 and the geodesic encircles the ellipsoid in a "transpolar" sense. The geodesic oscillates east and west of the ellipse X = 0; on each oscillation it completes slightly more than a full circuit around the ellipsoid. In the typical case, this results in the geodesic filling the area bounded by the two longitude lines ω = ω1 и ω = 180 ° - ω 1. Если a = b, все меридианы геодезические; эффект a ≠ b заставляет такие геодезические колебаться на восток и запад. Два примера на рис. 20 и 21. Сужение геодезической вблизи полюса исчезает в пределе b → c; в этом случае эллипсоид становится вытянутым эллипсоидом, и рис. 20 будет напоминать рис. 10 (повернутый на бок). Все касательные к трансполярной геодезической касаются конфокального двуполостного гиперболоида, который пересекает эллипсоид в точке ω = ω 1.

Рис. 22. Геодезическая шлангокабель, β 1 = 90 °, ω 1 = 0 °, α 1 = 135 °.

Если начальная точка β 1 = 90 °, ω 1 = 0 ° (точка пуповины) и α 1 = 135 ° (геодезическая выходит из эллипса Y = 0 под прямым углом), то γ = 0 и геодезическая многократно пересекает противоположную точку пуповины и возвращается в свою начальную точку. Однако на каждой схеме угла, под которым она пересекает Y = 0, становится ближе к 0 ° или 180 °, так что асимптотически геодезическая лежит на эллипсе Y = 0 (Hart 1849) (Arnold 1989, стр. 265), как показано на рис. 22. Одна геодезическая не заполняет область на эллипсоиде. Все касательные к омбилическим геодезическим касаются софокусной гиперболы, которая пересекает эллипсоид в точках омбилических точек.

Пупочные геодезические ресурсы, используемые интересными свойствами.

Через любую точку эллипсоида проходят геодезические шлангокабеля.
Геодезическое расстояние между противоположными точками шлангокабеля одинаково независимо от начального направления геодезических.
В то время как замкнутые геодезические на эллипсах X = 0 и Z = 0 устойчивы (геодезическая, изначально близкая к эллипсу и почти параллельная ему, остается близкой к эллипсу), замкнутая геодезическая на эллипсе Y = 0, которая проходит через все 4 точки омбилизации, экспоненциально нестабильно. Он будет возмущен, он выйдет из плоскости Y = 0 и перевернется, прежде чем вернуться, чтобы приблизиться к плоскости. (Это поведение может повторяться в зависимости от характера возмущения.)

Если начальная точка геодезической не является точкой пуповины, ее оболочка представляет собой астроиду с двумя вершинами, лежащими на β = −β 1 и два других на β = −β 1 и два других на β = −β ω = ω 1 + π. Геометрическое место разреза для A - это часть линии β = −β 1 между выступами.

Приложения

Прямые и обратные геодезические задачи больше не играют центральной роли в геодезии, как раньше. Вместо решения уравнивания геодезических сетей как двумерной задачи в сфероидальной тригонометрии, эти проблемы теперь решаются трехмерными методами (Vincenty Bowring 1978). Географические информационные системы ;

определение морских границ (ЮНКЛОС 2006 <ЮНКЛОС 2006);

в правилах Федерального управления гражданской авиации для зональной навигации (RNAV 2007);

метод измерения расстояния в Спортивном кодексе FAI (FAI 2018).

помочь мусульманам найти их направление в сторону Мекки

Согласно принципу наименьшего действия, многие проблемы в физике могут быть сформулированы как вариационная задача, аналогичная задаче для геодезических. Действительно, геодезическая проблема эквивалентно движению частиц, вынужденной двигаться по поверхности, но в остальном не подверженной никаким силам (Лаплас 1799a) (Hilbert Cohn-Vossen 1952, стр. 222). По этой причине геодезические на простых поверхностях, как эллипсоиды вращения или трехосные эллипс оиды, часто используются в качестве тестовых примеров »для изучения новых методов. Примеры включают:

развитие эллиптических интегралов (Legendre 1811) и эллиптических функций (Weierstrass 1861);
развитие дифференциальной геометрии (Gauss 1828)) (Christoffel 1869);
методы решения систем дифференциальных взаимных независимых переменных (Jacobi 1839);
исследование каустики (Jacobi 1891);
исследования числа и устойчивости периодических) орбит (Пуанкаре 1905);
в пределе c → 0, геодезические на трехосном эллипсоиде сводятся к случаю расширений динамических биллиардов ;
до произвольного числа измерений (Knörrer 1980);
геодезический поток на поверхности ( Berger 2010, гл. 12).

См. Также

Примечания

Ссылки

Внешние ссылки

Геодез и онлайн-библиография книг и статей по геодезическим на эллипсоидах.
Тестовый набор для геодезических, набор из 500000 геодезических для эллипсоида WGS84, вычисленных с использованием высокоточной арифметики.
инструмент NGS, реализующий Винсенти (1975).
geod (1), справочная страница для утилита PROJ для геодезических вычислений.
Реализация GeographicLib из Karney (2013).
Рисование геодезических на Google Maps.