Astroid

Математическая кривая Astroid Гипоциклоидная конструкция астроида. Astroid $x\; 2/3\; +\; y\; 2/3\; =\; r\; 2/3\; \{\backslash \; displaystyle\; x\; ^\; \{2/3\}\; +\; y\; ^\; \{2/3\}\; =\; r\; ^\; \{2/3\}\}$как общий конверт семейства эллипсов уравнения $(x\; /\; a)\; 2\; +\; (y\; /\; b)\; 2\; =\; r\; 2\; \{\backslash \; displaystyle\; (x\; /\; a)\; ^\; \{2\}\; +\; (y\; /\; b)\; ^\; \{2\}\; =\; r\; ^\; \{2\}\}$, где $a\; +\; b\; =\; 1\; \{\backslash \; displaystyle\; a\; +\; b\; =\; 1\}$. Огибающая лестницы (цветные линии в правом верхнем квадранте), скользящей по вертикальной стене, и его отражения (другие квадранты) - астроида. Средние точки очерчивают круг, а другие точки - эллипсы, как на предыдущем рисунке. В файле SVG наведите указатель мыши на лестницу, чтобы выделить ее. 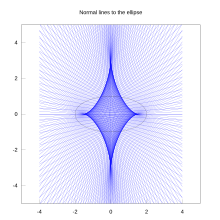Астроид как эволюция эллипса

астроид - это особая математическая кривая : гипоциклоид с четырьмя бугорками. В частности, это геометрическое место точки на окружности, когда она катится внутри фиксированной окружности с четырехкратным радиусом. При двойном генерировании это также геометрическое место точки на окружности, поскольку оно катится внутри фиксированного круга с радиусом в 4/3 раза больше. Его также можно определить как конверт линейного сегмента фиксированной длины, который перемещается, сохраняя конечную точку на каждой из осей. Следовательно, это оболочка движущейся планки в Trammel of Archimedes.

. Его современное название происходит от греческого слова, означающего «звезда ». Она была предложена, первоначально в форме «Astrois», Джозефом Иоганном фон Литтроу в 1838 году. Кривая имела множество названий, в том числе тетракуспид (используется до сих пор), кубоциклоида и парацикло . По форме он почти идентичен эволюции эллипса.

• 1 Уравнения
• 2 Вывод полиномиального уравнения
• 3 Метрические свойства
• 4 Свойства
• 5 См. Также
• 6 Ссылки
• 7 Внешние ссылки

Если радиус фиксированной окружности равен a, то уравнение задается следующим образом:

$x\; 2/3\; +\; y\; 2/3\; =\; a\; 2/3.\; \{\backslash \; displaystyle\; x\; ^\; \{2/3\}\; +\; y\; ^\; \{2/3\}\; =\; a\; ^\; \{2/3\}.\; \backslash ,\}$

Это означает, что астроид также является суперэллипсом.

Параметрические уравнения являются

$x\; =\; a\; cos\; 3\; \; t\; =\; a\; 4\; (3\; cos\; \; t\; +\; cos\; \; 3\; t),\; y\; =\; a\; sin\; 3\; \; t\; =\; a\; 4\; (3\; sin\; \; t\; -\; sin\; \; 3\; t).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; a\; \backslash \; cos\; ^\; \{3\}\; t\; =\; \{a\; \backslash \; over\; 4\}\; (3\; \backslash \; cos\; t\; +\; \backslash \; cos\; 3t),\; \backslash \backslash \; [6pt]\; y\; =\; a\; \backslash \; sin\; ^\; \{3\}\; t\; =\; \{a\; \backslash \; over\; 4\}\; (3\; \backslash \; sin\; t-\; \backslash \; sin\; 3t).\; \backslash \; end\; \{align\}\}\}$

Уравнение педали относительно начала координат:

$r\; 2\; =\; a\; 2–3\; p\; 2,\; \{\backslash \; displaystyle\; r\; ^\; \{2\}\; =\; a\; ^\; \{2\}\; -3p\; ^\; \{2\},\}$

уравнение Уэвелла равно

$s\; =\; 3\; a\; 4\; соз\; \; 2\; \phi ,\; \{\backslash \; displaystyle\; s\; =\; \{3a\; \backslash \; over\; 4\}\; \backslash \; cos\; 2\; \backslash \; varphi,\}$

и уравнение Чезаро равно

$R\; 2\; +\; 4\; s\; 2\; =\; 9\; a\; 2\; 4.\; \{\backslash \; displaystyle\; R\; ^\; \{2\}\; +\; 4s\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{9a\; ^\; \{2\}\}\; \{4\}\}.\}$

полярное уравнение is

$r\; =\; a\; (cos\; 2\; /\; 3\; \; \theta \; +\; sin\; 2/3\; \; \theta )\; 3/2.\; \{\backslash \; displaystyle\; r\; =\; \{\backslash \; frac\; \{a\}\; \{(\backslash \; cos\; ^\; \{2/3\}\; \backslash \; theta\; +\; \backslash \; sin\; ^\; \{2/3\}\; \backslash \; theta)\; ^\; \{3/2\}\}\}.\}$

Астроида - вещественное геометрическое место плоской алгебраической кривой рода ноль. Он имеет уравнение

$(x\; 2\; +\; y\; 2\; -\; a\; 2)\; 3\; +\; 27\; a\; 2\; x\; 2\; y\; 2\; =\; 0.\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; -a\; ^\; \{2\})\; ^\; \{3\}\; +\; 27a\; ^\; \{2\}\; x\; ^\; \{2\}\; y\; ^\; \{2\}\; =\; 0.\; \backslash ,\}$

Следовательно, астроида является реальной алгебраической кривой шестой степени.

Полиномиальное уравнение может быть получено из уравнения Лейбница с помощью элементарной алгебры:

$x\; 2/3\; +\; y\; 2/3\; =\; a\; 2/3.\; \{\backslash \; displaystyle\; x\; ^\; \{2/3\}\; +\; y\; ^\; \{2/3\}\; =\; a\; ^\; \{2/3\}.\; \backslash ,\}$

Куб с обеих сторон:

$x\; 6/3\; +\; 3\; x\; 4/3\; y\; 2/3\; +\; 3\; x\; 2/3\; y\; 4/3\; +\; y\; 6/3\; =\; a\; 6/3\; \{\backslash \; displaystyle\; x\; ^\; \{6/3\}\; +\; 3x\; ^\; \{4/3\}\; y\; ^\; \{2/3\}\; +\; 3x\; ^\; \{2/3\}\; y\; ^\; \{4/3\}\; +\; y\; ^\; \{6/3\}\; =\; a\; ^\; \{6/3\}\; \backslash ,\}$

$x\; 2\; +\; 3\; x\; 2/3\; y\; 2/3\; (x\; 2/3\; +\; y\; 2/3)\; +\; y\; 2\; =\; a\; 2\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; 3x\; ^\; \{2/3\}\; y\; ^\; \{2/3\}\; (x\; ^\; \{2/3\}\; +\; y\; ^\; \{\; 2/3\})\; +\; y\; ^\; \{2\}\; =\; a\; ^\; \{2\}\; \backslash ,\}$

$x\; 2\; +\; y\; 2\; -\; a\; 2\; =\; -\; 3\; x\; 2/3\; y\; 2/3\; (x\; 2/3\; +\; y\; 2\; /\; 3)\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; -a\; ^\; \{2\}\; =\; -\; 3x\; ^\; \{2/3\}\; y\; ^\; \{2/3\}\; (x\; ^\; \{2/3\}\; +\; y\; ^\; \{2/3\})\; \backslash ,\}$

Куб снова с обеих сторон:

$(x\; 2\; +\; y\; 2\; -\; a\; 2)\; 3\; =\; -\; 27\; x\; 2\; y\; 2\; (x\; 2/3\; +\; y\; 2/3)\; 3\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; -a\; ^\; \{2\})\; ^\; \{3\}\; =\; -\; 27x\; ^\; \{2\}\; y\; ^\; \{2\}\; (x\; ^\; \{2/3\}\; +\; y\; ^\; \{\; 2/3\})\; ^\; \{3\}\; \backslash ,\}$

Но поскольку:

$x\; 2/3\; +\; y\; 2/3\; =\; a\; 2/3\; \{\backslash \; displaystyle\; x\; ^\; \{2/3\}\; +\; y\; ^\; \{2\; /\; 3\}\; =\; a\; ^\; \{2/3\}\; \backslash ,\}$

Отсюда следует, что

$(x\; 2/3\; +\; y\; 2/3)\; 3\; =\; a\; 2.\; \{\backslash \; displaystyle\; (x\; ^\; \{2/3\}\; +\; y\; ^\; \{2/3\})\; ^\; \{3\}\; =\; a\; ^\; \{2\}.\; \backslash ,\}$

Следовательно:

$(x\; 2\; +\; y\; 2\; -\; a\; 2)\; 3\; =\; -\; 27\; x\; 2\; y\; 2\; a\; 2\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; -a\; ^\; \{2\})\; ^\; \{3\}\; =\; -\; 27x\; ^\; \{2\}\; y\; ^\; \{2\}\; a\; ^\; \{2\}\; \backslash ,\}$

или

$(x\; 2\; +\; y\; 2\; -\; a\; 2)\; 3\; +\; 27\; x\; 2\; y\; 2\; a\; 2\; =\; 0.\; \{\backslash \; displaystyle\; (x\; ^\; \{2\}\; +\; y\; ^\; \{\; 2\}\; -a\; ^\; \{2\})\; ^\; \{3\}\; +\; 27x\; ^\; \{2\}\; y\; ^\; \{2\}\; a\; ^\; \{2\}\; =\; 0.\; \backslash ,\}$

Закрытая площадь

$3\; 8\; \pi \; a\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{3\}\; \{8\}\}\; \backslash \; pi\; a\; ^\; \{2\}\}$

Длина кривой

$6\; a\; \{\backslash \; displaystyle\; 6a\}$

Объем поверхности вращения ограничивающая область вокруг оси x.

$32\; 105\; \pi \; a\; 3\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{32\}\; \{105\}\}\; \backslash \; pi\; a\; ^\; \{3\}\}$

Площадь поверхности вращения относительно x- ось

$12\; 5\; \pi \; a\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{12\}\; \{5\}\}\; \backslash \; pi\; a\; ^\; \{2\}\}$

Астроида имеет четыре точки возврата в реальной плоскости., точки на звезде. У него есть еще две сложные точки возврата на бесконечности и четыре комплексные двойные точки, всего десять особенностей.

Двойная кривая к астроиде - это крестообразная кривая с уравнением $x\; 2\; y\; 2\; =\; x\; 2\; +\; y\; 2.\; \{\backslash \; displaystyle\; \backslash \; textstyle\; x\; ^\; \{2\}\; y\; ^\; \{2\}\; =\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}.\}$эволюция астроиды дважды является астроидой такой же большой.

• Кардиоид (эпициклоида с одним бугорком)
• Нефроид (эпициклоида с двумя бугорками)
• Дельтовидный (гипоциклоид с тремя бугорками)
• Астроид Стоунера – Вольфарта использование этой кривой в магнетизме.
• Спирограф

• Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых. Dover Publications. С. 4 –5, 34–35, 173–174. ISBN 0-486-60288-5.
• Wells D (1991). Словарь любопытной и интересной геометрии Penguin. Нью-Йорк: Книги Пингвинов. С. 10–11. ISBN 0-14-011813-6.
• R.C. Йейтс (1952). «Астроид». Справочник по кривым и их свойствам. Анн-Арбор, Мичиган: Дж. У. Эдвардс. стр. 1 и далее.

Викискладе есть средства массовой информации, относящиеся к Astroid.

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик У. «Астроид». MathWorld.
• «Astroid» в архиве истории математики MacTutor
• «Astroid» в энциклопедии замечательных математических форм
• Статья на 2dcurves.com
• Визуальный словарь специальных плоских кривых, Кса Ли
• Bars of an Astroid от Шандора Кабая, The Wolfram Demonstrations Project.