Каталонское твердое тело

редактировать

Двойной многогранник к твердому телу Архимеда

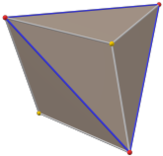
Тетраэдр Триакиса, пятиугольный икоситетраэдр и disdyakis triacontahedron. Первый и последний могут быть описаны как самые маленькие и самые большие каталонские твердые тела.

Твердые тела выше (темные) показаны вместе с их двойниками (светлые). Видимые части каталонских тел - это правильные пирамиды.

A ромбические додекаэдры с его конфигурацией граней.

В математике каталонское твердое тело, или двойственное архимедово, является двойным многогранником к архимедову твердому телу. Всего 13 каталонских твердых тел. Они названы в честь бельгийского математика Эжена Каталана, который впервые описал их в 1865 году.

Все каталонские твердые тела выпуклые. Они гранно-транзитивные, но не вершинно-транзитивные. Это связано с тем, что двойственные архимедовы тела транзитивны по вершинам и не транзитивны по граням. Обратите внимание, что в отличие от Платоновых тел и Архимедовых тел, грани каталонских тел не являются правильными многоугольниками. Однако вершины фигур каталонских тел правильные и имеют постоянные двугранные углы . Каталонские тела, будучи транзитивными по граням, являются изоэдрами.

Кроме того, два каталонских тела являются реберно-транзитивными : ромбический додекаэдр и ромбический триаконтаэдр. Это двойники двух квазирегулярных архимедовых тел.

Так же, как призмы и антипризмы обычно не считаются архимедовыми твердыми телами, так бипирамиды и трапеции обычно не рассматриваются Каталонские твердые тела, несмотря на то, что они переходят на поверхность.

Два каталонских твердых тела являются хиральными : пятиугольный икоситетраэдр и пятиугольный гексеконтаэдр, двойственный хиральному курносому кубу и курносый додекаэдр. Каждый из них состоит из двух энантиоморфов. Не считая энантиоморфов, бипирамид и трапецоэдров, всего существует 13 каталонских твердых тел.

n	архимедово твердое тело	каталонское твердое тело
1	усеченный тетраэдр	триакис-тетраэдр
2	усеченный куб	триакис-октаэдр
3	усеченный кубооктаэдр	дисдиакис додекаэдр
4	усеченный шестигранник-октаэдр
5	усеченный додекаэдр	триакис икосаэдр
6	усеченный икосододекаэдр	дисдиакис триаконтаэдр
7	усеченный икосаэдр	пентакис додекаэдр
8	кубооктаомбэдр	ромбидрон827 додекаэдр>10	ромбокубооктаэдр	дельтоидальный икоситетраэдр
11	ромбикосододекаэдр	дельтоидальный гексеконтаэдр
12	курносый куб	пятиугольный икоситетраэдр
снизу 809 <89 пятиугольный шестиугольник

Содержание

1 Симметрия
2 Список
3 Геометрия
- 3.1 Треугольные грани
- 3.2 Четырехугольные грани
- 3.3 Пятиугольные грани
- 3.4 Метрические свойства
- 3.5 Применение к другим твердым телам
4 См. также
5 Ссылки
6 Внешние ссылки

Симметрия

Каталонские твердые тела, наряду с их двойными архимедовыми телами, могут быть сгруппированы в те, которые обладают тетраэдрической, октаэдрической и икосаэдрической симметрией. Как для октаэдрической, так и для икосаэдрической симметрии существует шесть форм. Единственное каталонское твердое тело с подлинной тетраэдрической симметрией - это триакис-тетраэдр (двойственный усеченному тетраэдру ). Ромбический додекаэдр и тетракис-шестигранник имеют октаэдрическую симметрию, но их можно раскрасить, чтобы иметь только тетраэдрическую симметрию. Исправление и пренебрежение также существуют с тетраэдрической симметрией, но они платонические вместо архимедова, поэтому их двойники платонические, а не каталонские. (Они показаны на коричневом фоне в таблице ниже.)

Тетраэдрическая симметрия
Архимедова. (Платоническая)
Каталонская. (Платоническая)

Октаэдрическая симметрия
Архимед
Каталонский

Икосаэдрическая симметрия
Архимед
Каталонский

Список

Имя. (Двойное имя). Имя Конвея	Грань. многоугольник	Углы граней (°)	Двугранный угол (°)	Грани	Ребра	Верт	Сим.
триакис-тетраэдр. (усеченный тетраэдр ). «kT»	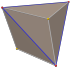Равнобедренный. . V3.6.6	112,885. 33,557. 33,557	129,521	12	18	8	Td
ромбический додекаэдр. (кубооктаэдр ). «jC»	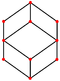Ромб. . V3.4.3.4	70.529. 109.471. 70.529. 109.471	120	12	24	14	Oh
трехугольный октаэдр. (усеченный куб ). «kO»	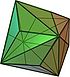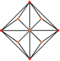Равнобедренный. . V3.8.8	117.201. 31.400. 31.400	147,35 0	24	36	14	Oh
тетракис-шестигранник. (усеченный октаэдр ). «kC»	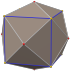Равнобедренный. . V4.6.6	83.621. 48.190. 48.190	143.130	24	36	14	Oh
дельтоидальный икоситетраэдр. (ромбокубооктаэдр ). «oC»	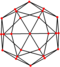воздушный змей. . V3.4.4.4	81,579. 81,579. 81,579. 115,263	138.118	24	48	26	Oh
disdyakis dodecahedron. (усеченный кубооктаэдр ). «mC»	Scalene. . V4.6.8	87.202. 55.025. 37.773	155.082	48	72	26	Oh
пятиугольный икоситетраэдр. (курносый куб ). "gC"	Пентагон. . V3.3.3.3.4	114.812. 114.812. 114.812. 114.812. 80.752	136.309	24	60	38	O
ромбический триаконтаэдр. (икосододекаэдр ). "jD"	Ромб. . V3.5.3.5	63.435. 116.565. 63.435. 116.565	144	30	60	32	Ih
триакис-икосаэдр. (усеченный додекаэдр ). «kI»	Равнобедренный. . V3.10.10	119.039. 30.480. 30.480	160.613	60	90	32	Ih
додекаэдр пентакиса. (усеченный икосаэдр ). «кД»	Равнобедренный. . V5.6.6	68,619. 55,691. 55,691	156,719	60	90	32	Ih
дельтоидальный гексеконтаэдр. (ромбикосододекаэдр ). "oD"	Воздушный змей. . V3.4.5.4	86.974. 67.783. 86.974. 118.269	154.121	60	120	62	Ih
триаконтаэдр Дисдиакиса. (усеченный икосододекаэдр ). "mD"	Скален. . V4.6.10	88.992. 58.238. 32.770	164.888	120	180	62	Ih
пятиугольный шестигранник. (курносый додекаэдр ). "gD"	Пентагон. . V3.3.3.3.5	118.137. 118.137. 118.137. 118.137. 67.454	153.179	60	150	92	I

Геометрия

Все двугранные углы каталонского твердого тела равны. Обозначая их значение как $θ {\ displaystyle \ theta}$ $\ theta$ и обозначая угол лица в вершинах, где $p {\ displaystyle p}$ $p$ грани встречаются как $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ , имеем

sin ⁡ (θ / 2) = cos ⁡ (π / p) / cos ⁡ (α p / 2) { \ displaystyle \ sin (\ theta / 2) = \ cos (\ pi / p) / \ cos (\ alpha _ {p} / 2)}

{\ displaystyle \ sin (\ theta / 2) = \ cos (\ pi / p) / \ cos (\ alpha _ {p} / 2)}

Это можно использовать для вычисления $θ {\ displaystyle \ theta}$ $\ theta$ и $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ , $α q {\ displaystyle \ alpha _ {q}}$ $\ alpha _ {q}$ ,..., только из $p {\ displaystyle p}$ $p$ , $q {\ displaystyle q}$ $q$ ...

Треугольные грани

Из 13 каталонских тел 7 имеют треугольные грани. Они имеют вид Vp.qr, где p, q и r принимают значения из 3, 4, 5, 6, 8 и 10. Углы $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ , $α q {\ displaystyle \ alpha _ {q}}$ $\ alpha _ {q}$ и $α r {\ displaystyle \ alpha _ {r}}$ $\ alpha _ {r}$ можно вычислить следующим образом. Положим $a = 4 cos 2 ⁡ (π / p) {\ displaystyle a = 4 \ cos ^ {2} (\ pi / p)}$ ${\ displaystyle a = 4 \ соз ^ {2} (\ pi / p)}$ , $b = 4 cos 2 ⁡ (π / q) {\ displaystyle b = 4 \ cos ^ {2} (\ pi / q)}$ ${\ displaystyle b = 4 \ cos ^ {2} (\ pi / q)}$ , $c = 4 cos 2 ⁡ (π / r) {\ displaystyle c = 4 \ cos ^ {2} (\ pi / r)}$ ${\ displaystyle c = 4 \ cos ^ {2} (\ pi / r)}$ и положите

S = - a 2 - b 2 - c 2 + 2 ab + 2 bc + 2 ca {\ displaystyle S = -a ^ {2} -b ^ {2} -c ^ {2} + 2ab + 2bc + 2ca}

{\ displaystyle S = -a ^ {2 } -b ^ {2} -c ^ {2} + 2ab + 2bc + 2ca}

Тогда

cos ⁡ (α p) = S 2 bc - 1 {\ displaystyle \ cos (\ alpha _ {p}) = {\ frac {S} {2bc}} - 1}

{\ displaystyle \ cos (\ alpha _ {p}) = {\ frac {S} {2bc}} - 1}

грех ⁡ (α p / 2) = - a + b + c 2 bc {\ displaystyle \ sin (\ alpha _ {p} / 2) = {\ frac {-a + b + c} {2 {\ sqrt {bc}}}}

{\ displaystyle \ sin (\ alpha _ {p} / 2) = {\ frac {-a + b + c} {2 {\ sqrt {bc}}}} }

Для $α q {\ displaystyle \ alpha _ {q}}$ $\ alpha _ {q}$ и $α r {\ displaystyle \ alpha _ {r}}$ $\ alpha _ {r}$ выражения, конечно, похожи. двугранный угол $θ {\ displaystyle \ theta}$ $\ theta$ можно вычислить из

cos ⁡ (θ) = 1-2 abc / S {\ displaystyle \ cos ( \ theta) = 1-2abc / S}

{ \ displaystyle \ cos (\ theta) = 1-2abc / S}

Применяя это, например, к триаконтаэдру дисдиакиса ( $p = 4 {\ displaystyle p = 4}$ $p=4$ , $q = 6 { \ displaystyle q = 6}$ ${\ displaystyle q = 6}$ и $r = 10 {\ displaystyle r = 10}$ ${\ displaystyle r = 10}$ , следовательно, $a = 2 {\ displaystyle a = 2}$ ${\ displaystyle a = 2}$ , $b = 3 {\ displaystyle b = 3}$ ${\ displaystyle b = 3}$ и $c = ϕ + 2 {\ displaystyle c = \ phi +2}$ ${\ displaystyle c = \ phi +2}$ , где $ϕ {\ displaystyle \ phi}$ $\ phi$ - золотое сечение ) дает $cos ⁡ (α 4) = 2 - ϕ 6 (2 + ϕ) = 7 - 4 ϕ 30 {\ displaystyle \ cos (\ alpha _ {4}) = {\ frac {2- \ phi} {6 (2+ \ phi)}} = {\ frac {7-4 \ phi} {30}}}$ ${\ displaystyle \ cos (\ alpha _ {4}) = {\ frac {2- \ phi} {6 (2+ \ phi)}} = {\ frac {7-4 \ phi} {30}}}$ и $соз ⁡ (θ) = - 10-7 ϕ 14 + 5 ϕ = - 48 ϕ - 155 241 {\ displaystyle \ cos (\ theta) = {\ frac {-10-7 \ phi} {14 +5 \ phi}} = {\ frac {-48 \ phi -155} {241}}}$ ${\ displaystyle \ cos (\ theta) = {\ frac {-10-7 \ phi} {14 + 5 \ phi}} = {\ frac {-48 \ phi -155} {241}}}$ .

Четырехугольные грани

Из 13 каталонских тел 4 имеют четырехугольные грани. Они имеют вид Vp.qpr, где p, q и r принимают свои значения из числа 3, 4 и 5. Угол $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ может вычисляется по следующей формуле:

cos ⁡ (α p) = 2 cos 2 ⁡ (π / p) - cos 2 ⁡ (π / q) - cos 2 ⁡ (π / r) 2 cos 2 ⁡ (π / п) + 2 соз ⁡ (π / q) соз ⁡ (π / г) {\ Displaystyle \ соз (\ альфа _ {р}) = {\ гидроразрыва {2 \ соз ^ {2} (\ пи / р) - \ cos ^ {2} (\ pi / q) - \ cos ^ {2} (\ pi / r)} {2 \ cos ^ {2} (\ pi / p) +2 \ cos (\ pi / q) \ cos (\ pi / r)}}}

{\ displaystyle \ cos (\ alpha _ {p}) = {\ frac {2 \ cos ^ {2} (\ pi / p) - \ cos ^ { 2} (\ pi / q) - \ cos ^ {2} (\ pi / r)} {2 \ cos ^ {2} (\ pi / p) +2 \ cos (\ pi / q) \ cos (\ pi / r)}}}

Отсюда $α q {\ displaystyle \ alpha _ {q}}$ $\ alpha _ {q}$ , $α r {\ displaystyle \ alpha _ {r}}$ $\ alpha _ {r}$ и двугранный угол легко вычислить. В качестве альтернативы положите $a = 4 cos 2 ⁡ (π / p) {\ displaystyle a = 4 \ cos ^ {2} (\ pi / p)}$ ${\ displaystyle a = 4 \ соз ^ {2} (\ pi / p)}$ , $b = 4 cos 2 ⁡ (π / q) {\ displaystyle b = 4 \ cos ^ {2} (\ pi / q)}$ ${\ displaystyle b = 4 \ cos ^ {2} (\ pi / q)}$ , $c = 4 cos 2 ⁡ (π / p) + 4 cos ⁡ (π / q) cos ⁡ (π / r) { \ displaystyle c = 4 \ cos ^ {2} (\ pi / p) +4 \ cos (\ pi / q) \ cos (\ pi / r)}$ ${\ displaystyle c = 4 \ cos ^ {2} (\ pi / p) +4 \ cos (\ pi / q) \ cos (\ pi / r)}$ . Тогда $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ и $α q {\ displaystyle \ alpha _ {q}}$ $\ alpha _ {q}$ можно найти, применив формулы для треугольного случая. Угол $α r {\ displaystyle \ alpha _ {r}}$ $\ alpha _ {r}$ , конечно, можно вычислить аналогичным образом. Грани являются воздушными змеями или, если $q = r {\ displaystyle q = r}$ $q = r$ , ромбами. Применяя это, например, к дельтовидному икоситетраэдру ( $p = 4 {\ displaystyle p = 4}$ $p=4$ , $q = 3 {\ displaystyle q = 3}$ $q = 3$ и $r = 4 {\ displaystyle r = 4}$ $r = 4$ ), получаем $cos ⁡ (α 4) = 1 2 - 1 4 2 {\ displaystyle \ cos (\ alpha _ {4 }) = {\ frac {1} {2}} - {\ frac {1} {4}} {\ sqrt {2}}}$ ${ \ displaystyle \ cos (\ alpha _ {4}) = {\ frac {1} {2}} - {\ frac {1} {4}} {\ sqrt {2}}}$ .

Пятиугольные грани

Из 13 каталонских тел 2 имеют пятиугольные грани. Они имеют форму Vp.pppq, где p = 3 и q = 4 или 5. Угол $α p {\ displaystyle \ alpha _ {p}}$ $\ alpha _ {p}$ может быть вычислен путем решения Уравнение третьей степени:

8 cos 2 ⁡ (π / p) cos 3 ⁡ (α p) - 8 cos 2 ⁡ (π / p) cos 2 ⁡ (α p) + cos 2 ⁡ (π / q) = 0 {\ displaystyle 8 \ cos ^ {2} (\ pi / p) \ cos ^ {3} (\ alpha _ {p}) - 8 \ cos ^ {2} (\ pi / p) \ cos ^ {2 } (\ alpha _ {p}) + \ cos ^ {2} (\ pi / q) = 0}

{\ displaystyle 8 \ cos ^ {2} (\ pi / p) \ cos ^ {3} (\ alpha _ {p}) - 8 \ cos ^ {2} (\ pi / p) \ cos ^ {2} (\ alpha _ {p}) + \ cos ^ {2} (\ pi / q) = 0}

Метрические свойства

Для каталонского твердого тела $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ пусть $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ будет двойным по отношению к средней сфере из $С {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ . Тогда $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ - это архимедово твердое тело с той же средней сферой. Обозначим длину краев $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ как $l {\ displaystyle l}$ $l$ . Пусть $r {\ displaystyle r}$ $r$ будет inradius граней $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ , $rm {\ displaystyle r_ {m}}$ $r_m$ средний радиус $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ и $A {\ displaystyle {\ bf {A} }}$ ${\ displaystyle {\ bf {A}}}$ , $ri {\ displaystyle r_ {i}}$ $r_ {i}$ внутренний радиус $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ и $rc {\ displaystyle r_ {c}}$ $r_{c}$ радиус описанной окружности $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ . Тогда эти величины можно выразить в $l {\ displaystyle l}$ $l$ и двугранном угле $θ {\ displaystyle \ theta}$ $\ theta$ следующим образом:

r 2 знак равно l 2 8 (1 - соз ⁡ θ) {\ displaystyle r ^ {2} = {\ frac {l ^ {2}} {8}} (1- \ cos \ theta)}

{\ displaystyle г ^ {2} = {\ гидроразрыва {l ^ {2}} {8}} (1- \ cos \ theta)}

rm 2 = l 2 4 1 - соз ⁡ θ 1 + соз ⁡ θ {\ displaystyle r_ {m} ^ {2} = {\ frac {l ^ {2}} {4}} {\ frac {1- \ cos \ theta} { 1+ \ соз \ тета}}

{\ displaystyle r_ {m } ^ {2} = {\ frac {l ^ {2}} {4}} {\ frac {1- \ cos \ theta} {1+ \ cos \ theta}}}

ри 2 = l 2 8 (1 - соз ⁡ θ) 2 1 + соз ⁡ θ {\ displaystyle r_ {i} ^ {2} = {\ frac {l ^ { 2}} {8}} {\ frac {(1- \ cos \ theta) ^ {2}} {1+ \ cos \ theta}}}

{\ displaystyle r_ {i} ^ {2} = {\ frac {l ^ {2}} {8}} {\ гидроразрыва {(1- \ соз \ тета) ^ {2}} {1+ \ соз \ тета}}}

rc 2 = l 2 2 1 1 + cos ⁡ θ { \ displaystyle r_ {c} ^ {2} = {\ frac {l ^ {2}} {2}} {\ frac {1} {1+ \ cos \ theta}}}

{\ displaystyle r_ {c} ^ {2} = {\ frac {l ^ {2}} {2}} {\ frac {1} {1+ \ cos \ theta}}}

Эти величины связаны соотношением $rm 2 = ri 2 + r 2 {\ displaystyle r_ {m} ^ {2} = r_ {i} ^ {2} + r ^ {2}}$ ${\ displaystyle r_ {m} ^ {2} = r_ {i} ^ {2} + r ^ {2}}$ , $rc 2 = rm 2 + l 2/4 {\ displaystyle r_ {c} ^ {2} = r_ {m} ^ {2} + l ^ {2} / 4}$ ${\ displaystyle r_ {c} ^ {2} = r_ {m} ^ {2} + l ^ {2} / 4}$ и $rirc = rm 2 {\ displaystyle r_ {i} r_ {c} = r_ {m} ^ {2}}$ ${\ отображает tyle r_ {i} r_ {c} = r_ {m} ^ {2}}$ .

В качестве примера пусть $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ будет кубооктаэдром с длиной ребра $l = 1 {\ displaystyle l = 1}$ $l = 1$ . Тогда $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ - ромбический додекаэдр. Применение формулы для четырехугольников с $p = 4 {\ displaystyle p = 4}$ $p=4$ и $q = r = 3 {\ displaystyle q = r = 3}$ ${\ displaystyle q = r = 3}$ дает $соз ⁡ θ = - 1/2 {\ displaystyle \ cos \ theta = -1 / 2}$ ${\ displaystyle \ cos \ theta = -1 / 2}$ , следовательно, $ri = 3/4 {\ displaystyle r_ {i} = 3 / 4}$ ${\ displaystyle r_ {i} = 3/4}$ , $rm = 1 2 3 {\ displaystyle r_ {m} = {\ frac {1} {2}} {\ sqrt {3}}}$ ${\ displaystyle r_ {m} = {\ frac {1} {2}} {\ sqrt {3}}}$ , $rc = 1 {\ displaystyle r_ {c} = 1}$ ${\ di splaystyle r_ {c} = 1}$ , $r = 1 4 3 {\ displaystyle r = {\ frac {1} {4}} {\ sqrt {3}}}$ ${ \ displaystyle r = {\ frac {1} {4}} {\ sqrt {3}}}$ .

Все вершины $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ типа $p {\ displaystyle p}$ $p$ лежат на сфере с радиусом $rc, p {\ displaystyle r_ {c, p}}$ ${\ displaystyle r_ {c, p}}$ задается

rc, p 2 = ri 2 + 2 r 2 1 - cos ⁡ α p {\ displaystyle r_ {c, p} ^ {2} = r_ {i} ^ {2} + {\ frac {2r ^ {2}} {1- \ cos \ alpha _ {p}}}}

{\ displaystyle r_ {c, p } ^ {2} = r_ {i} ^ {2} + {\ frac {2r ^ {2}} {1- \ cos \ alpha _ {p}}}}

и аналогично для $q, r,… {\ displaystyle q, r, \ ldots}$ ${\ displaystyle q, r, \ ldots}$ .

Двойная сфера касается всех граней $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ , которые являются правильными $p {\ displaystyle p}$ $p$ -угольников (и аналогично для $q, r,… {\ displaystyle q, r, \ ldots}$ ${\ displaystyle q, r, \ ldots}$ ) в их центре. Радиус $ri, p {\ displaystyle r_ {i, p}}$ ${\ диспла ystyle r_ {я, p}}$ этой сферы определяется как

ri, p 2 = rm 2 - l 2 4 cot 2 ⁡ (π / p) {\ displaystyle r_ {i, p} ^ {2} = r_ {m} ^ {2} - {\ frac {l ^ {2}} {4}} \ cot ^ {2} (\ pi / p)}

{\ displaystyle r_ {i, p} ^ {2} = r_ {m} ^ {2} - {\ frac {l ^ {2}} {4}} \ cot ^ {2} (\ pi / p)}

Эти два радиуса связаны соотношением $ri, prc, p = rm 2 {\ displaystyle r_ {i, p} r_ {c, p} = r_ {m} ^ {2}}$ ${\ displaystyle r_ {i, p} r_ {c, p} = r_ {m} ^ {2}}$ . Продолжая приведенный выше пример: $cos ⁡ α 3 = - 1/3 {\ displaystyle \ cos \ alpha _ {3} = - 1/3}$ ${\ displaystyle \ cos \ alpha _ {3} = - 1/3}$ и $cos ⁡ α 4 = 1 / 3 {\ displaystyle \ cos \ alpha _ {4} = 1/3}$ ${\ displaystyle \ cos \ alpha _ {4} = 1 / 3}$ , что дает $rc, 3 = 3 8 6 {\ displaystyle r_ {c, 3} = {\ frac {3} {8}} {\ sqrt {6}}}$ ${\ displaystyle r_ {c, 3} = {\ frac {3} {8}} {\ sqrt {6}}}$ , $rc, 4 = 3 4 2 {\ displaystyle r_ {c, 4} = {\ frac {3} {4}} {\ sqrt {2 }}}$ ${\ displaystyle r_ {c, 4} = {\ frac {3} {4}} {\ sqrt {2}}}$ , $ri, 3 = 1 3 6 {\ displaystyle r_ {i, 3} = {\ frac {1} {3}} {\ sqrt {6}}}$ ${\ displaystyle r_ {i, 3} = {\ frac {1} {3}} {\ sqrt {6}}}$ и $ri, 4 = 1 2 2 {\ displaystyle r_ {i, 4} = {\ frac {1} {2}} {\ sqrt {2}}}$ ${\ displaystyle r_ {i, 4} = {\ frac {1} {2}} {\ sqrt {2}}}$ .

Если $P {\ displaystyle P}$ $P$ - вершина $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ типа $p {\ displaystyle p}$ $p$ , $e {\ displaystyle e}$ $e$ край $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ , начиная с $P {\ displaystyle P}$ $P$ , и $P ′ {\ displaystyle P ^ {\ prime}}$ $P ^ {\ prime}$ точка, в которой край $e {\ displaystyle e}$ $e$ касается средней части $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ , обозначает расстояние $PP ′ {\ displaystyle PP ^ {\ prime} }$ ${\ displaystyle PP ^ {\ prime}}$ по $l p {\ displaystyle l_ {p}}$ ${ \ displaystyle l_ {p}}$ . Затем ребра $C {\ displaystyle {\ bf {C}}}$ ${\ displaystyle {\ bf { C}}}$ соединяют вершины типа $p {\ displaystyle p}$ $p$ и типа $q {\ displaystyle q}$ $q$ имеют длину $lp, q = lp + lq {\ displaystyle l_ {p, q} = l_ {p} + l_ {q}}$ ${\ displaystyle l_ {p, q } = l_ {p} + l_ {q}}$ . Эти величины можно вычислить с помощью

lp = l 2 cos ⁡ (π / p) sin ⁡ (α p / 2) {\ displaystyle l_ {p} = {\ frac {l} {2}} {\ frac { \ cos (\ pi / p)} {\ sin (\ alpha _ {p} / 2)}}}

{\ displaystyle l_ {p} = {\ frac {l} {2}} {\ frac {\ cos (\ pi / p)} {\ sin (\ alpha _ {p} / 2)}}}

и аналогично для $q, r,… {\ displaystyle q, r, \ ldots}$ ${\ displaystyle q, r, \ ldots}$ . Продолжая приведенный выше пример: $грех ⁡ (α 3/2) = 1 3 6 {\ displaystyle \ sin (\ alpha _ {3} / 2) = {\ frac {1} {3}} {\ sqrt { 6}}}$ ${\ displaystyle \ sin (\ alpha _ {3} / 2) = {\ frac {1} {3}} {\ sqrt {6}}}$ , $грех ⁡ (α 4/2) = 1 3 3 {\ displaystyle \ sin (\ alpha _ {4} / 2) = {\ frac {1} {3}} {\ sqrt {3 }}}$ ${\ displaystyle \ sin (\ alpha _ {4} / 2) = {\ frac {1} {3}} {\ sqrt {3}}}$ , $l 3 = 1 8 6 {\ displaystyle l_ {3} = {\ frac {1} {8}} {\ sqrt {6}}}$ ${\ displaystyle l_ {3} = {\ frac {1} {8}} {\ sqrt { 6}}}$ , $l 4 = 1 4 6 {\ displaystyle l_ {4} = {\ frac {1} {4}} {\ sqrt {6}}}$ ${\ displaystyle l_ {4} = {\ frac {1} {4}} {\ sqrt {6}}}$ , поэтому ребра ромбического додекаэдра имеют длину $l 3, 4 = 3 8 6 {\ displaystyle l_ {3,4} = {\ frac {3} {8}} {\ sqrt {6}}}$ ${\ displaystyle l_ {3,4} = {\ frac {3} {8}} {\ sqrt { 6}}}$ .

Двугранные углы $α p, q {\ displaystyle \ alpha _ {p, q}}$ ${\ displaystyle \ alpha _ {p, q}}$ между $p {\ displaystyle p}$ $p$ -gonal и $q {\ displaystyle q}$ $q$ -gonal Face of $A {\ displaystyle {\ bf {A}}}$ ${\ displaystyle {\ bf {A}}}$ удовлетворяет

cos ⁡ α p, q = l 2 4 детская кроватка ⁡ (π / p) детская кроватка ⁡ (π / q) rm 2 - ri, pri, qrm 2 = lplq - rm 2 rc, prc, q {\ displaystyle \ cos \ alpha _ {p, q} = {\ frac {l ^ {2}} {4}} {\ frac {\ cot ( \ pi / p) \ cot (\ pi / q)} {r_ {m} ^ {2}}} - {\ frac {r_ {i, p} r_ {i, q}} {r_ {m} ^ { 2}}} = {\ frac {l_ {p} l_ {q} -r_ {m} ^ {2 }} {r_ {c, p} r_ {c, q}}}}

{\ displaystyle \ cos \ alpha _ {p, q} = {\ frac {l ^ {2}} {4}} {\ frac {\ cot (\ pi / p) \ cot (\ pi / q)} {r_ {m} ^ {2}}} - {\ frac {r_ {i, p} r_ {i, q}} {r_ {m} ^ {2}}} = {\ frac {l_ {p} l_ {q} -r_ {m} ^ {2}} {r_ {c, p} r_ {c, q}}}}

Завершение примера с ромбическим додекаэдром, двугранный угол $α 3, 4 {\ displaystyle \ alpha _ {3,4}}$ ${\ displaystyle \ alpha _ {3,4}}$ кубооктаэдра определяется как $cos ⁡ α 3, 4 = - 1 3 3 {\ displaystyle \ cos \ alpha _ {3,4} = - {\ frac {1} {3}} {\ sqrt {3}}}$ ${\ displaystyle \ cos \ alpha _ {3,4} = - {\ frac {1 } {3}} {\ sqrt {3}}}$ .

Применение к другим твердым телам

Все формулы этого раздела применимы к Платоновым телам и бипирамидам и трапецоэдры также с равными двугранными углами, поскольку они могут быть получены только из свойства постоянного двугранного угла. Для пятиугольного трапецоэдра, например, с гранями V3.3.5.3, мы получаем $cos ⁡ (α 3) = 1 4 - 1 4 5 {\ displaystyle \ cos (\ alpha _ { 3}) = {\ frac {1} {4}} - {\ frac {1} {4}} {\ sqrt {5}}}$ ${\ displaystyle \ cos (\ alpha _ {3}) = {\ frac {1} {4}} - {\ frac {1} {4}} {\ sqrt {5 }}}$ или $α 3 = 108 ∘ { \ Displaystyle \ alpha _ {3} = 108 ^ {\ circ}}$ ${\ displaystyle \ alpha _ {3} = 108 ^ {\ circ}}$ . Это неудивительно: можно отрезать обе вершины таким образом, чтобы получить правильный додекаэдр.

См. Также

Список однородных мозаик Показывает двойные однородные многоугольные мозаики, похожие на каталонский solids
Нотация многогранника Конвея Процесс построения нотации
Архимедово твердое тело
Твердое тело Джонсона

Ссылки

Эжен Каталонский Память о Теории Полиэдров. J. l'École Polytechnique (Paris) 41, 1-71, 1865.
Формы, пространство и симметрия. New York: Dover, 1991.
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325 -5, MR 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X.(Раздел 3-9)
Энтони Пью (1976). Многогранники: визуальный подход. Калифорния: Калифорнийский университет Press в Беркли. ISBN 0-520-03056-7.Глава 4: Двойники архимедовых многогранников, призмы и антиприз

Внешние ссылки

На Викискладе есть материалы, связанные с Каталонские твердые вещества.

Вайсштейн, Эрик У. "Каталонские твердые вещества". MathWorld.
Вайсштейн, Эрик У. «Изоэдр». MathWorld.
Catalan Solids - в Visual Polyhedra
Archimedean duals - в Virtual Reality Polyhedra
Interactive Catalan Solid in Java
Ссылка для скачивания оригинальной публикации Catalan 1865 года - с красивыми рисунками, формат PDF