Войти
Алгоритм умножения является алгоритм (или метод), чтобы умножить два числа. В зависимости от размера чисел используются разные алгоритмы. Эффективные алгоритмы умножения существуют с момента появления десятичной системы счисления.
Метод сетки (или метод ящика) - это вводный метод многозначного умножения, который часто преподают ученикам в начальной или начальной школе. С конца 1990-х годов он является стандартной частью национальной учебной программы по математике в начальной школе в Англии и Уэльсе.
Оба фактора разбиваются («разбиваются») на их сотни, десятки и единицы частей, и затем произведения частей вычисляются в явном виде на относительно простой стадии только умножения, прежде чем эти вклады затем суммируются, чтобы дать окончательный ответ в виде отдельный этап сложения.
Например, вычисление 34 × 13 может быть вычислено с использованием сетки:
300 40 90 + 12 ———— 442
| × | 30 | 4 |
|---|---|---|
| 10 | 300 | 40 |
| 3 | 90 | 12 |
с последующим сложением, чтобы получить 442, либо в виде единой суммы (см. справа), либо путем формирования итоговых значений строка за строкой (300 + 40) + (90 + 12) = 340 + 102 = 442.
Этот метод расчета (хотя и не обязательно с явным расположением сетки) также известен как алгоритм частичных произведений. Его суть заключается в раздельном вычислении простых умножений, при этом все сложение оставляется на заключительном этапе сбора.
Метод сетки в принципе может применяться к факторам любого размера, хотя количество субпродуктов становится громоздким по мере увеличения количества цифр. Тем не менее, это рассматривается как полезный явный метод для введения идеи многозначного умножения; и в эпоху, когда большинство вычислений умножения выполняется с помощью калькулятора или электронной таблицы, на практике это может быть единственным алгоритмом умножения, который когда-либо понадобится некоторым студентам.
Если используется позиционная система счисления, естественный способ умножения чисел преподается в школах в виде длинного умножения, иногда называемого умножением в начальной школе, иногда называемого стандартным алгоритмом: умножьте множимое на каждую цифру множителя, а затем сложите все правильно сдвинутые результаты. Это требует запоминания таблицы умножения на однозначные числа.
Это обычный алгоритм ручного умножения больших чисел по основанию 10. Компьютеры изначально использовали очень похожий алгоритм сдвига и сложения с основанием 2, но современные процессоры оптимизировали схему для быстрого умножения с использованием более эффективных алгоритмов по цене более сложных. аппаратная реализация. Человек, выполняющий длинное умножение на бумаге, запишет все произведения и сложит их вместе; Счеты -user подведут продукты, как только каждый из них вычисляется.
В этом примере используется длинное умножение для умножения 23 958 233 (множимое) на 5 830 (множитель) и получается 139 676 498 390 для результата (произведения).
23958233 × 5830 ——————————————— 00000000 ( = 23,958,233 × 0) 71874699 ( = 23,958,233 × 30) 191665864 ( = 23,958,233 × 800) + 119791165 ( = 23,958,233 × 5,000) ——————————————— 139676498390 ( = 139,676,498,390 )
Ниже псевдокод описывает процесс вышеупомянутого умножения. Он сохраняет только одну строку, чтобы сохранить сумму, которая в конечном итоге становится результатом. Обратите внимание, что оператор '+ =' используется для обозначения суммы существующего значения и операции сохранения (сродни таким языкам, как Java и C) для компактности.
multiply(a[1..p], b[1..q], base) // Operands containing rightmost digits at index 1 product = [1..p+q] // Allocate space for result for b_i = 1 to q // for all digits in b carry = 0 for a_i = 1 to p // for all digits in a product[a_i + b_i - 1] += carry + a[a_i] * b[b_i] carry = product[a_i + b_i - 1] / base product[a_i + b_i - 1] = product[a_i + b_i - 1] mod base product[b_i + p] = carry // last digit comes from final carry return product
Пусть п будет общее количество цифр в двух входных чисел в базовой D. Если результат необходимо сохранить в памяти, то сложность пространства тривиально равна ( n). Однако в некоторых приложениях нет необходимости хранить весь результат в памяти, и вместо этого цифры результата можно передавать в потоковом режиме по мере их вычисления (например, в системную консоль или файл). В этих сценариях длинное умножение имеет то преимущество, что его можно легко сформулировать как алгоритм пространства журнала ; то есть алгоритм, которому требуется только рабочее пространство, пропорциональное логарифму числа цифр во входных данных ( Θ (log n)). Это двойной логарифм умножаемых чисел (log log N). Обратите внимание, что сами операнды по-прежнему необходимо хранить в памяти, и их пространство Θ ( n) не рассматривается в этом анализе.
Метод основан на наблюдении, что каждую цифру результата можно вычислить справа налево, зная только перенос из предыдущего шага. Пусть a i и b i будут i-й цифрой операнда, с дополнениями a и b слева нулями, чтобы иметь длину n, r i - i-я цифра результата, а c i - перенос, сгенерированный для r i (i = 1 - самая правая цифра), то
или
Простой индуктивный аргумент показывает, что перенос никогда не может превышать n, а общая сумма для r i никогда не может превышать D * n: перенос в первый столбец равен нулю, а для всех остальных столбцов в столбце не более n цифр., и перенос не более n из предыдущего столбца (по предположению индукции). Сумма не превышает D * n, а перенос в следующий столбец не превышает D * n / D или n. Таким образом, оба этих значения могут быть сохранены в O (log n) цифрах.
В псевдокоде алгоритм лог-пространства:
multiply(a[1..p], b[1..q], base) // Operands containing rightmost digits at index 1 tot = 0 for ri = 1 to p + q - 1 // For each digit of result for bi = MAX(1, ri - p + 1) to MIN(ri, q) // Digits from b that need to be considered ai = ri − bi + 1 // Digits from a follow "symmetry" tot = tot + (a[ai] * b[bi]) product[ri] = tot mod base tot = floor(tot / base) product[p+q] = tot mod base // Last digit of the result comes from last carry return product
Некоторые микросхемы реализуют длинное умножение аппаратно или в микрокоде для различных размеров целых чисел и слов с плавающей запятой. В арифметике произвольной точности обычно используется длинное умножение с базовым значением 2 w, где w - количество битов в слове, для умножения относительно небольших чисел.
Чтобы умножить два числа на n цифр с помощью этого метода, потребуется около n 2 операций. Более формально: используя метрику натурального размера, состоящую из числа цифр, временная сложность умножения двух n- значных чисел с использованием длинного умножения составляет Θ ( n 2).
При программной реализации алгоритмы длинного умножения должны иметь дело с переполнением во время сложения, что может быть дорогостоящим. Типичное решение состоит в том, чтобы представить число в малой системе счисления, b, так, чтобы, например, 8 b было представимым машинным целым числом. Затем можно выполнить несколько добавлений до того, как произойдет переполнение. Когда число становится слишком большим, мы добавляем его часть к результату или переносим и отображаем оставшуюся часть обратно на число, которое меньше b. Этот процесс называется нормализацией. Ричард Брент использовал этот подход в своем пакете Fortran, MP.
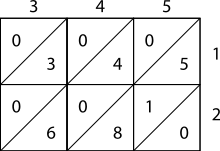Сначала настройте сетку, пометив ее строки и столбцы числами, которые нужно умножить. Затем заполните поля цифрами десятков в верхних треугольниках и цифрами единиц внизу. 
Наконец, просуммируйте диагональные участки и перенесите по мере необходимости, чтобы получить ответ. Решетчатое или решетчатое умножение алгоритмически эквивалентно длинному умножению. Это требует подготовки решетки (сетки, нарисованной на бумаге), которая направляет вычисления и отделяет все умножения от сложений. Он был введен в Европе в 1202 году в фибоначчиевого «s Liber Abaci. Фибоначчи описал эту операцию как мысленную, используя свою правую и левую руки для выполнения промежуточных вычислений. Матракчи Насух представил 6 различных вариантов этого метода в своей книге XVI века «Умдет-уль Хисаб». Он широко использовался в школах Эндеруна по всей Османской империи. Кости Напьера или стержни Непьера также использовали этот метод, опубликованный Напье в 1617 году, в год его смерти.
Как показано в примере, множимое и множитель написаны сверху и справа от решетки или сита. Он находится в «Арифметике» Мухаммада ибн Мусы аль-Хорезми, одном из источников Леонардо, упомянутых Сиглером, автором «Liber Abaci Фибоначчи», 2002.
На рисунках справа показано, как вычислить 345 × 12 с помощью решеточного умножения. В качестве более сложного примера рассмотрим рисунок ниже, на котором показано вычисление 23 958 233, умноженное на 5 830 (множитель); результат 139 676 498 390. Замечание 23 958 233 находится вдоль вершины решетки, а 5 830 - вдоль правой стороны. Продукты заполняют решетку, и сумма этих продуктов (по диагонали) находится вдоль левой и нижней сторон. Затем эти суммы суммируются, как показано.
2 3 9 5 8 2 3 3 +---+---+---+---+---+---+---+---+- |1 /|1 /|4 /|2 /|4 /|1 /|1 /|1 /| | / | / | / | / | / | / | / | / | 5 01|/ 0|/ 5|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5| +---+---+---+---+---+---+---+---+- |1 /|2 /|7 /|4 /|6 /|1 /|2 /|2 /| | / | / | / | / | / | / | / | / | 8 02|/ 6|/ 4|/ 2|/ 0|/ 4|/ 6|/ 4|/ 4| +---+---+---+---+---+---+---+---+- |0 /|0 /|2 /|1 /|2 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 3 17|/ 6|/ 9|/ 7|/ 5|/ 4|/ 6|/ 9|/ 9| +---+---+---+---+---+---+---+---+- |0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 0 24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0| +---+---+---+---+---+---+---+---+- 26 15 13 18 17 13 09 00 | 01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390 |
= 139,676,498,390 |
Бинарный метод также известен как крестьянское умножение, потому что он широко использовался людьми, которых относили к крестьянам и, следовательно, не запомнили таблицы умножения, необходимые для длительного умножения. Алгоритм использовался в Древнем Египте. Его основные преимущества заключаются в том, что его можно быстро обучить, не нужно запоминать и можно выполнять с помощью жетонов, таких как фишки для покера, если нет бумаги и карандаша. Недостатком является то, что для этого требуется больше шагов, чем для длинного умножения, поэтому он может быть громоздким для больших чисел.
На бумаге запишите в один столбец числа, которые вы получите, когда многократно уменьшите множитель вдвое, игнорируя остаток; в столбце рядом с ним несколько раз удвойте множимое. Вычеркните каждую строку, в которой последняя цифра первого числа четная, и сложите оставшиеся числа во втором столбце, чтобы получить продукт.
В этом примере используется крестьянское умножение, чтобы умножить 11 на 3, чтобы получить результат 33.
Decimal: Binary: 11 3 1011 11 5 6 101 110 2121011001 24 1 11000 —— —————— 33 100001
Подробное описание шагов:
Метод работает, потому что умножение распределительное, поэтому:
Более сложный пример с использованием цифр из предыдущих примеров (23 958 233 и 5 830):
Decimal: Binary: 583023958233101101100011010110110110010010110110012915 47916466 101101100011 10110110110010010110110010 1457 95832932 10110110001 101101101100100101101100100 72819166586410110110001011011011001001011011001000364383331728101101100101101101100100101101100100001827666634561011011010110110110010010110110010000091 1533326912 1011011 1011011011001001011011001000000 45 3066653824 101101 10110110110010010110110010000000 2261333076481011010110110110010010110110010000000011 12266615296 1011 1011011011001001011011001000000000 5 24533230592 101 10110110110010010110110010000000000 249066461184101011011011001001011011001000000000001 98132922368 1 1011011011001001011011001000000000000 ———————————— 1022143253354344244353353243222210110 (before carry) 139676498390 10000010000101010111100011100111010110
Это разновидность крестьянского умножения.
В базе 2 длинное умножение сводится к почти тривиальной операции. Для каждого бита «1» в умножителе сдвиньте множимое на соответствующую величину, а затем просуммируйте сдвинутые значения. В некоторых процессорах быстрее использовать битовые сдвиги и сложения, чем инструкции умножения, особенно если множитель маленький или всегда один и тот же.
Исторически сложилось так, что компьютеры использовали алгоритм «сдвиг и сложение» для умножения небольших целых чисел. Обе базы 2 длинного умножение и основание 2 крестьянское умножение сводятся к этому же алгоритму. В базе 2 умножение на одну цифру множителя сводится к простой серии логических операций И. Каждый частичный продукт добавляется к текущей сумме, как только вычисляется каждый частичный продукт. Большинство доступных в настоящее время микропроцессоров реализуют этот или другие подобные алгоритмы (например, кодирование Бута ) для различных целочисленных размеров и размеров с плавающей запятой в аппаратных умножителях или в микрокоде.
На доступных в настоящее время процессорах команда побитового сдвига быстрее, чем команда умножения, и может использоваться для умножения (сдвиг влево) и деления (сдвиг вправо) на степени двойки. Умножение на константу и деление на константу можно реализовать с помощью последовательности сдвигов и сложений или вычитаний. Например, есть несколько способов умножить на 10, используя только битовый сдвиг и сложение.
((x lt;lt; 2) + x) lt;lt; 1 # Here 10*x is computed as (x*2^2 + x)*2 (x lt;lt; 3) + (x lt;lt; 1) # Here 10*x is computed as x*2^3 + x*2
В некоторых случаях такие последовательности сдвигов и сложений или вычитаний будут превосходить аппаратные умножители и особенно делители. Деление на номер формы или часто может быть преобразовано в такую короткую последовательность.
Эти типы последовательностей всегда должны использоваться для компьютеров, у которых нет инструкции «умножения», а также могут использоваться путем расширения чисел с плавающей запятой, если заменить сдвиги вычислением 2 * x как x + x, поскольку эти логически эквивалентны.
Две величины можно умножить на четверть квадрата, применив следующее тождество, включающее функцию минимума, которую некоторые источники приписывают вавилонской математике (2000–1600 гг. До н.э.).
Если один из x + y и x - y нечетный, другой тоже нечетный, то есть их квадраты равны 1 по модулю 4, тогда взятие пола уменьшает оба на четверть; затем вычитание отменяет четверти, а отбрасывание остатков не вносит никакой разницы по сравнению с тем же выражением без функций пола. Ниже приведена справочная таблица четверть квадратов с отброшенным остатком для цифр от 0 до 18; это позволяет умножать числа до 9 × 9.
| п | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| ⌊ п 2 / 4⌋ | 0 | 0 | 1 | 2 | 4 | 6 | 9 | 12 | 16 | 20 | 25 | 30 | 36 | 42 | 49 | 56 | 64 | 72 | 81 год |
Если, например, вы хотите умножить 9 на 3, вы заметите, что сумма и разница равны 12 и 6 соответственно. Если посмотреть на оба этих значения в таблице, получим 36 и 9, разница между которыми составляет 27, что является произведением 9 и 3.
Антуан Вуазен опубликовал в 1817 году таблицу квадратов от 1 до 1000 в качестве помощи в умножении. Более крупная таблица квадратов от 1 до 100000 была опубликована Сэмюэлем Лонди в 1856 году, а таблица от 1 до 200000 - Джозефом Блатером в 1888 году.
Умножители на четверть квадрата использовались в аналоговых компьютерах для формирования аналогового сигнала, который был произведением двух аналоговых входных сигналов. В этом приложении сумма и разность двух входных напряжений формируются с помощью операционных усилителей. Квадрат каждого из них аппроксимируется с помощью кусочно-линейных схем. Наконец, разница между двумя квадратами формируется и масштабируется с коэффициентом в одну четверть с использованием еще одного операционного усилителя.
В 1980 году Эверетт Л. Джонсон предложил использовать метод четверти квадрата в цифровом умножителе. Например, чтобы сформировать произведение двух 8-битных целых чисел, цифровое устройство формирует сумму и разность, просматривает обе величины в таблице квадратов, берет разность результатов и делит на четыре, сдвигая два бита в Правильно. Для 8-битных целых чисел таблица четверть квадратов будет иметь 2 9 -1 = 511 записей (одна запись для полного диапазона 0..510 возможных сумм, различия с использованием только первых 256 записей в диапазоне 0..255) или 2 9 -1 = 511 записи ( с использованием отрицательных разностей техники 2-дополнений и 9-битового маскирования, что позволяет избежать тестирования знак различия), каждая запись является 16-разрядный (значения входа являются из (0² / 4) = От 0 до (510² / 4) = 65025).
Метод умножения на четверть квадрата также принес пользу 8-битным системам, которые не поддерживают аппаратный умножитель. Чарльз Патни реализовал это в 6502.
Какой алгоритм умножения двухзначных чисел самый быстрый ?
(больше нерешенных проблем в информатике)Комплексное умножение обычно включает четыре умножения и два сложения.
Или
Но есть способ уменьшить количество умножений до трех.
Произведение ( a + bi) ( c + di) можно рассчитать следующим образом.
Этот алгоритм использует только три умножения, а не четыре, и пять сложений или вычитаний, а не два. Если умножение дороже, чем три сложения или вычитания, как при ручном вычислении, то скорость увеличивается. На современных компьютерах умножение и сложение могут занимать примерно одинаковое время, поэтому увеличения скорости может не быть. Есть компромисс в том, что при использовании с плавающей запятой может быть некоторая потеря точности.
Для быстрых преобразований Фурье (БПФ) (или любого линейного преобразования ) комплексные умножения производятся на постоянные коэффициенты c + di (называемые множителями в БПФ), и в этом случае два сложения ( d - c и c + d) могут быть предварительно вычислены.. Следовательно, требуется только три умножения и три прибавления. Однако подобный обмен умножения на сложение может оказаться невыгодным с современными модулями с плавающей запятой.
Для систем, которым необходимо умножать числа в диапазоне нескольких тысяч цифр, таких как системы компьютерной алгебры и библиотеки bignum, длинное умножение выполняется слишком медленно. Эти системы могут использовать умножение Карацубы, которое было открыто в 1960 г. (опубликовано в 1962 г.). Суть метода Карацубы заключается в наблюдении, что двузначное умножение может быть выполнено только с тремя, а не с четырьмя умножениями, которые обычно требуются. Это пример того, что сейчас называется алгоритмом «разделяй и властвуй». Предположим, мы хотим умножить два двузначных числа с основанием m: x 1 m + x 2 и y 1 m + y 2:
Чтобы вычислить эти три произведения чисел с основанием m, мы можем снова использовать тот же трюк, эффективно используя рекурсию. После того, как числа вычислены, нам нужно сложить их вместе (шаги 4 и 5), что потребует примерно n операций.
Умножение Карацубы имеет временную сложность O ( n log 2 3) ≈ O ( n 1,585), что делает этот метод значительно более быстрым, чем длинное умножение. Из-за накладных расходов на рекурсию умножение Карацубы происходит медленнее, чем длинное умножение для малых значений n ; поэтому типичные реализации переключаются на длинное умножение для малых значений n.
Алгоритм Карацубы был первым известным алгоритмом умножения, который асимптотически быстрее, чем длинное умножение, и поэтому может рассматриваться как отправная точка для теории быстрых умножений.
В 1963 году Петр Унгер предложил установки м в I, чтобы получить аналогичное сокращение сложного алгоритма умножения. Чтобы умножить ( a + bi) ( c + di), выполните следующие действия:
Как и в алгоритме из предыдущего раздела, для этого требуется три умножения и пять сложений или вычитаний.
Другой метод умножения называется Тоом – Кука или Тоом-3. Метод Тоома – Кука разбивает каждое число, которое нужно умножить, на несколько частей. Метод Тоома – Кука является одним из обобщений метода Карацубы. Трехсторонний Тоом – Кука может выполнить умножение размера 3N за стоимость пяти умножений размера N. Это ускоряет операцию в 9/5 раз, а метод Карацубы ускоряет ее в 4/3.
Хотя использование все большего и большего числа частей может еще больше сократить время, затрачиваемое на рекурсивное умножение, накладные расходы, связанные с добавлением и управлением цифрами, также растут. По этой причине метод преобразования Фурье обычно быстрее для чисел с несколькими тысячами цифр и асимптотически быстрее для еще больших чисел.
Демонстрация умножения 1234 × 5678 = 7006652 с использованием быстрого преобразования Фурье (БПФ). Используются теоретико-числовые преобразования целых чисел по модулю 337, выбирая 85 в качестве корня 8-й степени из единицы. База 10 используется вместо базы 2 w в иллюстративных целях. Основная идея Штрассена (1968) заключается в использовании быстрого полиномиального умножения для выполнения быстрого целочисленного умножения. Алгоритм был реализован на практике, и в 1971 году Шёнхаге и Штрассен предоставили теоретические гарантии, что привело к созданию алгоритма Шёнхаге-Штрассена. Детали следующие: Мы выбираем наибольшее целое число w, которое не вызовет переполнения во время процесса, описанного ниже. Затем мы разбиваем два числа на m групп по w битов следующим образом:
Мы смотрим на эти числа как на многочлены от x, где x = 2 w, чтобы получить,
Тогда мы можем сказать, что
Ясно, что вышеупомянутая установка реализуется полиномиальным умножением двух полиномов a и b. Решающим шагом сейчас является использование быстрого умножения Фурье многочленов, чтобы реализовать указанные выше умножения быстрее, чем за наивное время O ( m 2).
Чтобы оставаться в модульной установке преобразований Фурье, мы ищем кольцо с корнем (2 m) -й степени из единицы. Следовательно, мы выполняем умножение по модулю N (и, следовательно, в кольце Z / NZ). Кроме того, N должно быть выбрано так, чтобы не было «циклического перехода», по сути, никаких сокращений по модулю N не происходило. Таким образом, выбор N имеет решающее значение. Например, это можно сделать так:
Кольцо Z / NZ, таким образом, будет иметь корень (2 m) -й степени из единицы, а именно 8. Кроме того, можно проверить, что c k lt; N, и, таким образом, циклического перехода не произойдет.
Алгоритм имеет временную сложность Θ ( n log ( n) log (log ( n))) и используется на практике для чисел с более чем 10 000-40 000 десятичных знаков. В 2007 году это было улучшено Мартином Фюрером ( алгоритм Фюрера ), чтобы получить временную сложность n log ( n) 2 Θ ( log * ( n)) с использованием преобразований Фурье по комплексным числам. Аниндья Де, Чандан Саха, Пиюш Курур и Рампрасад Саптариши предложили аналогичный алгоритм с использованием модульной арифметики в 2008 году, достигнув того же времени работы. В контексте вышеупомянутого материала последние авторы достигли того, что нашли N намного меньше 2 3 k + 1, так что Z / NZ имеет корень (2 m) -й степени из единицы. Это ускоряет вычисления и снижает временную сложность. Однако эти последние алгоритмы быстрее, чем Шёнхаге – Штрассен, только для непрактично больших входных данных.
В марте 2019 года Дэвид Харви и Джорис ван дер Ховен выпустили документ, описывающий алгоритм умножения O ( n log n).
Использование теоретико-числовых преобразований вместо дискретных преобразований Фурье позволяет избежать проблем с ошибками округления за счет использования модульной арифметики вместо арифметики с плавающей запятой. Чтобы применить разложение, которое позволяет БПФ работать, длина преобразования должна быть факторизована для малых простых чисел и должна быть множителем N - 1, где N - размер поля. В частности, вычисление с использованием поля Галуа GF ( k 2), где k - простое число Мерсенна, позволяет использовать преобразование со степенью 2; например, k = 2 31 - 1 поддерживает размеры преобразования до 2 32.
Существует тривиальная нижняя граница Ω ( n) для умножения двух n -битных чисел на одном процессоре; ни алгоритм сопоставления (на обычных машинах, то есть на машинах, эквивалентных Тьюрингу), ни какая-либо более точная нижняя граница неизвестна. Умножение лежит вне AC 0 [ p ] для любого простого p, что означает, что не существует семейства схем постоянной глубины, полиномиального (или даже субэкспоненциального) размера, использующих элементы AND, OR, NOT и MOD p, которые могут вычислить произведение. Это следует из постоянного уменьшения MOD q до умножения. Нижние оценки умножения известны также для некоторых классов ветвящихся программ.
Все вышеперечисленные алгоритмы умножения также могут быть расширены для умножения многочленов. Например, алгоритм Штрассена может использоваться для умножения полиномов. В качестве альтернативы можно использовать метод подстановки Кронекера для преобразования задачи умножения полиномов в единичное двоичное умножение.
Методы длинного умножения можно обобщить, чтобы разрешить умножение алгебраических формул:
14ac - 3ab + 2 multiplied by ac - ab + 1
14ac -3ab 2 ac -ab 1 ———————————————————— 14a2c2 -3a2bc 2ac -14a2bc 3 a2b2 -2ab 14ac -3ab 2 ——————————————————————————————————————— 14a2c2 -17a2bc 16ac 3a2b2 -5ab +2 =======================================
В качестве еще одного примера умножения на основе столбцов рассмотрите умножение 23 длинных тонн (t), 12 центнеров (cwt) и 2 четвертей (qtr) на 47. В этом примере используются меры энирдупуа : 1 t = 20 cwt, 1 cwt = 4 qtr.
t cwt qtr 23 12 2 47 x ———————————————— 141 94 94 940 470 29 23 ———————————————— 1110 587 94 ———————————————— 1110 7 2 ================= Answer: 1110 ton 7 cwt 2 qtr
Сначала умножьте четверти на 47, результат 94 записывается в первую рабочую область. Затем умножьте cwt 12 * 47 = (2 + 10) * 47, но пока не складывайте частичные результаты (94, 470). Аналогичным образом умножьте 23 на 47, получив (141, 940). Столбец кварталов суммируется, а результат помещается во вторую рабочую область (в данном случае - тривиальный ход). 94 четверти - это 23 центнера и 2 четверти, поэтому поместите 2 в ответ и поместите 23 в следующий столбец слева. Теперь сложите три записи в столбце cwt, получив 587. Это 29 t 7 cwt, поэтому запишите 7 в ответ и 29 в столбец слева. Теперь сложите столбец тонн. Никаких настроек не требуется, поэтому результат просто копируется.
Та же самая схема и методы могут использоваться для любых традиционных измерений и недесятичных валют, таких как старая британская система £ sd.
