Решеточное умножение, также известный как итальянский метод, Китайский метод, Китайская решетка, умножение гелозии, умножение сита, шабах, по диагонали или Венецианские квадраты - это метод умножения, который использует решетку для умножения двух многозначных чисел. Математически он идентичен более часто используемому алгоритму длинного умножения, но разбивает процесс на более мелкие шаги, которые некоторым практикам легче использовать.
Этот метод возник еще в средневековье., который веками использовался во многих культурах. Он все еще преподается в некоторых учебных программах.
Составлена сетка, каждая ячейка разделена по диагонали. Два множимого произведения, которое нужно вычислить, записываются вдоль верхней и правой стороны решетки, соответственно, с одной цифрой на столбец в верхней части для первого множимого (число, записываемое слева направо), и по одной цифре в каждой строке вниз с правой стороны для второго множимого (число, записанное сверху вниз). Затем каждая ячейка решетки заполняется произведением ее цифры столбца и строки.
В качестве примера рассмотрим умножение 58 на 213. После записи множимых по бокам рассмотрите каждую ячейку, начиная с верхней левой ячейки. В этом случае цифра столбца равна 5, а цифра строки - 2. Запишите их произведение, 10, в ячейку, указав цифру 1 над диагональю и цифру 0 под диагональю (см. Рисунок для шага 1).
Если в простом произведении отсутствует цифра в разряде десятков, просто заполните разряды десятков цифрой 0.
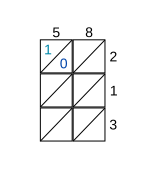 Шаг 1
Шаг 1 После того, как все ячейки будут заполнены таким образом, цифры в каждой диагонали суммируются, работая от правой нижней диагонали к верхней левой. Каждая диагональная сумма записывается там, где заканчивается диагональ. Если сумма содержит более одной цифры, значение разряда десятков переносится на следующую диагональ (см. Шаг 2).
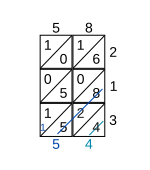 Шаг 2
Шаг 2 Цифры заполняются слева и снизу сетки, и ответ - числа, считанные снизу (слева) и поперек (снизу). В показанном примере результат умножения 58 на 213 равен 12354.
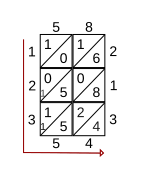 Шаг 3
Шаг 3 Метод решетки также можно использовать для умножения десятичных дробей. Например, умножение 5,8 на 2,13 происходит так же, как умножение 58 на 213, как описано в предыдущем разделе. Чтобы найти положение десятичной точки в окончательном ответе, можно провести вертикальную линию от десятичной точки в 5.8 и горизонтальную линию от десятичной точки в 2.13. (См. Рисунок к шагу 4.) Диагональ сетки через пересечение этих двух линий определяет положение десятичной точки в результате. В показанном примере результат умножения 5,8 и 2,13 равен 12,354.
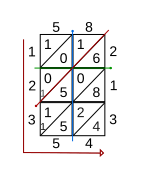 Шаг 4
Шаг 4 Решетчатое умножение исторически использовалось во многих различных культурах. Неизвестно, где он возник вначале и развивался ли он независимо более чем в одном регионе мира. Самое раннее зарегистрированное использование решеточного умножения:
Математик и педагог Дэвид Юджин Смит утверждал, что решеточное умножение было принесено в Италию из средний Восток. Это подкрепляется упоминанием того, что арабский термин, обозначающий метод, шабах, имеет то же значение, что и итальянский термин, обозначающий метод gelosia, а именно металлическая решетка или решетка (решетка) для окна.
Иногда ошибочно утверждается, что решеточное умножение было описано Мухаммадом ибн Мусой аль-Хваризми (Багдад, ок. 825) или Фибоначчи в его Liber Abaci (Италия, 1202, 1228). На самом деле, однако, ни один из этих двух авторов не нашел использования решеточного умножения. В главе 3 своей Liber Abaci, Фибоначчи действительно описывает родственную технику умножения на то, что он назвал quadrilatero in forma scacherii («прямоугольник в форме шахматной доски»). В этой технике квадратные ячейки не разделяются по диагонали; в каждую ячейку записывается только цифра самого низкого порядка, в то время как любую цифру более высокого порядка необходимо запомнить или записать в другом месте, а затем «перенести», чтобы добавить в следующую ячейку. Это отличается от решеточного умножения, отличительной чертой которого является то, что каждая ячейка прямоугольника имеет собственное правильное место для цифры переноса; это также означает, что ячейки можно заполнять в любом желаемом порядке. Свец сравнивает и противопоставляет умножение с помощью gelosia (решетки), scacherii (шахматной доски) и других табличных методов.
Другие известные исторические применения решеточного умножения включают:
Выводы этого метода также появились в работах 16 века Умдет-уль Хисаба Османско-боснийского polymath Matrakçı Nasuh. Треугольная версия метода умножения Matrakçı Nasuh показана в примере, показывающем 155 x 525 справа, и объясняется в примере, показывающем 236 x 175 на левом рисунке.

тот же принцип, описанный Матракчи Насух , лежал в основе более позднего развития счетных стержней, известных как кости Напьера (Шотландия, 1617 г.) и правители Генайи-Лукаса (Франция, поздний 1800-е годы).