Альфапедия

Правильное ускорение

редактировать
Карты и взгляды путешественников на одно-целое ускорение в состоянии покоя в течение одного года. Пространство-время путешественника для постоянного ускорения туда и обратно.

В теории относительности, собственное ускорение - это физическое ускорение (т. е. измеряемое ускорение с помощью акселерометра ). объектом. Таким образом, это ускорение относительно свободного падения, или инерционного наблюдателя, который на мгновение находится в состоянии покоя относительно измеряемого объекта. Следовательно, гравитация не вызывает надлежащего ускорения, поскольку гравитация действует на инерциального наблюдателя, от которого должно отклоняться любое правильное ускорение. Следствием этого является то, что все инерционные наблюдатели всегда имеют собственное ускорение, равное нулю.

Правильное ускорение контрастирует с координатным ускорением, которое зависит от выбора систем координат и, таким образом, от выбора наблюдателей (см. трехкратное ускорение в специальной теории относительности ).

В стандартных инерциальных координатах специальной теории относительности для однонаправленного движения собственное ускорение - это скорость изменения собственной скорости относительно координатного времени.

В инерциальной системе отсчета, в которой объект на мгновение находится в состоянии покоя, правильный 3-вектор ускорения в сочетании с нулевой составляющей времени дает четырехкратное ускорение объекта, что делает правильным -величина ускорения Лоренц-инвариант. Таким образом, концепция полезна: (i) с ускоренными системами координат, (ii) с релятивистскими скоростями и (iii) в искривленном пространстве-времени.

В ускоряющейся ракете после запуска или даже в ракете, стоящей на портале, правильное ускорение - это ускорение, которое ощущают находящиеся в нем люди, и которое описывается как g-force (что не сила, а ускорение; см. эту статью для более подробного обсуждения правильного ускорения), передаваемого только транспортным средством. «Ускорение свободного падения» («сила тяжести») никогда не способствует правильному ускорению ни при каких обстоятельствах, и, таким образом, правильное ускорение, которое ощущают наблюдатели, стоящие на земле, происходит из-за механической силы от земли, а не из-за «силы "или" ускорение свободного падения ". Если земля удалена, а наблюдателю разрешено свободное падение, наблюдатель будет испытывать координатное ускорение, но не будет надлежащего ускорения, и, следовательно, не будет перегрузки. Как правило, объекты в таком падении или вообще любой такой баллистический путь (также называемый инерционным движением), включая объекты на орбите, не испытывают надлежащего ускорения (без учета малых приливных ускорений для инерционных путей в гравитационных полях). Это состояние также известно как «невесомость» («невесомость») или «свободное падение», и оно вызывает ощущение невесомости.

Правильное ускорение сводится к координатному ускорению в инерциальной системе координат на плоской поверхности. пространство-время (т.е. в отсутствие гравитации), при условии, что величина собственной скорости объекта (импульс на единицу массы) намного меньше скорости света c. Только в таких ситуациях координатное ускорение полностью ощущается как перегрузочная сила (т. Е. Собственное ускорение, также определяемое как ускорение, создающее измеримый вес).

В ситуациях, когда гравитация отсутствует, но выбранная система координат не инерциальна, а ускоряется наблюдателем (например, ускоренная система отсчета ускоряющейся ракеты или рамка, закрепленная на объектах в центрифуге), то перегрузки и соответствующие собственные ускорения, ощущаемые наблюдателями в этих системах координат, вызваны механическими силами, которые противостоят их весу в таких системах. Этот вес, в свою очередь, создается фиктивными силами или «силами инерции», которые проявляются во всех таких ускоренных системах координат, подобно весу, создаваемому «силой тяжести» в системах, где объекты фиксируются в пространстве относительно гравитирующего тела (как на поверхности Земли).

Общая (механическая) сила, которая рассчитывается для создания надлежащего ускорения покоящейся массы в системе координат, которая имеет правильное ускорение, по закону Ньютона F = m a, называется надлежащей силой . Как видно выше, надлежащая сила равна силе противодействия, которая измеряется как «рабочий вес» объекта (то есть его вес, измеряемый таким устройством, как пружинные весы, в вакууме, в системе координат объекта). Таким образом, собственная сила, действующая на объект, всегда равна его измеренному весу и противоположна ему.

Содержание
  • 1 Примеры
  • 2 Классические приложения
    • 2.1 Перед запуском снаряда
    • 2.2 После запуска снаряда
  • 3 Вид из плоского пространственно-временного среза
    • 3.1 Ускорение в (1 + 1) D
  • 4 В искривленном пространстве-времени
    • 4.1 Сила и эквивалентность
    • 4.2 Обитатели поверхности на планете
    • 4.3 Четырехвекторные производные
  • 5 См. Также
  • 6 Сноски
  • 7 Внешние ссылки
Примеры

Когда держитесь за карусель, которая вращается с постоянной угловой скоростью, вы испытываете собственное ускорение радиально внутрь (центростремительное ) из-за взаимодействия между рукояткой и твоя рука. Это отменяет радиально направленное наружу геометрическое ускорение, связанное с вашей вращающейся системой координат. Это внешнее ускорение (с точки зрения вращающейся рамки) станет координатным ускорением, когда вы отпустите, заставляя вас улетать по пути с нулевым собственным ускорением (геодезический ). Неускоренные наблюдатели, конечно же, в их кадре просто видят ваше равное собственное и координатное ускорение исчезают, когда вы отпускаете.

Точно так же, стоя на невращающейся планете (и на Земле для практических целей), мы испытываем собственное ускорение вверх из-за нормальной силы, действующей со стороны Земли на подошву наших ботинок. Это отменяет нисходящее геометрическое ускорение из-за нашего выбора системы координат (так называемая рама-оболочка). Это нисходящее ускорение становится координированным, если мы непреднамеренно сойдем со скалы на траекторию с нулевым собственным ускорением (геодезической или дождевой системой координат).

Обратите внимание, что геометрические ускорения (из-за члена связи в ковариантной производной системы координат ниже) действуют на каждую унцию нашего существа, в то время как собственное ускорение обычно вызывается внешняя сила. На вводных курсах физики нисходящее (геометрическое) ускорение силы тяжести часто рассматривается как следствие силы, пропорциональной массе. Это, наряду с упорным избеганием неускоренных кадров, позволяет им рассматривать правильное и согласованное ускорение как одно и то же.

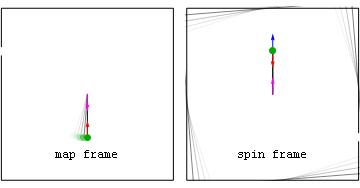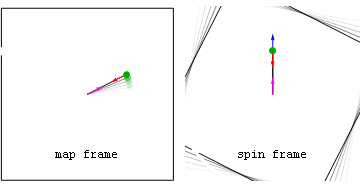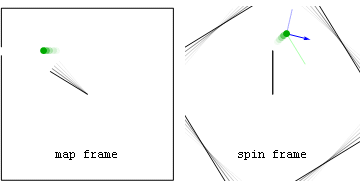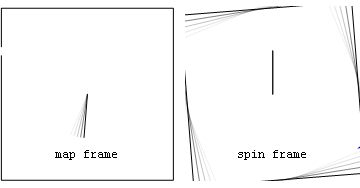
Даже тогда, если объект поддерживает постоянное собственное ускорение из состояния покоя в течение длительного периода в плоском пространстве-времени, наблюдатели в кадре покоя увидят уменьшение координатного ускорения объекта по мере приближения его координатной скорости к скорости света. Тем не менее, скорость увеличения собственной скорости объекта остается постоянной.

Таким образом, различие между собственным ускорением и координатным ускорением позволяет проследить опыт ускоренных путешественников с различных неньютоновских точек зрения. Эти перспективы включают точки зрения ускоренных систем координат (таких как карусель), высоких скоростей (где собственное время и время координат различаются) и искривленного пространства-времени (например, связанного с гравитацией на Земле).

Классические приложения

На низких скоростях в инерциальных системах координат из ньютоновской физики правильное ускорение просто равно координатному ускорению a=dx/ dt. Однако, как было рассмотрено выше, оно отличается от координатного ускорения, если кто-то решает (вопреки совету Ньютона) описывать мир с точки зрения ускоренной системы координат, такой как автомобиль, ускоряющийся от покоя, или камень, вращающийся в рогатке. Если кто-то решит признать, что гравитация вызвана кривизной пространства-времени (см. Ниже), правильное ускорение отличается от координатного ускорения в гравитационном поле.

. Например, объект, подвергнутый физическому или собственному ускорению ao, будет быть замеченным наблюдателями в системе координат, испытывающей постоянное ускорение aкадр, чтобы иметь координатное ускорение:

a → acc = a → o - a → frame {\ displaystyle {\ vec {a}} _ {acc } = {\ vec {a}} _ {o} - {\ vec {a}} _ {frame}}{\ vec {a}} _ {acc} = {\ vec {a}} _ {o} - {\ vec {a}} _ {frame} .

Таким образом, если объект ускоряется вместе с кадром, наблюдатели, прикрепленные к кадру, вообще не увидят ускорения.

Аналогично, объект, испытывающий физическое или собственное ускорение ao, будет замечен наблюдателями в кадре, вращающемся с угловой скоростью ω, чтобы иметь координатное ускорение:

a → rot = a → o - ω → × (ω → × r →) - 2 ω → × v → rot - d ω → dt × r → {\ displaystyle {\ vec {a}} _ {rot} = {\ vec {a}} _ { o} - {\ vec {\ omega}} \ times ({\ vec {\ omega}} \ times {\ vec {r}}) - 2 {\ vec {\ omega}} \ times {\ vec {v} } _ {rot} - {\ frac {d {\ vec {\ omega}}} {dt}} \ times {\ vec {r}}}{\vec {a}}_{rot}={\vec {a}}_{o}-{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})-2{\vec {\omega }}\times {\vec {v}}_{rot}-{\frac {d{\vec {\omega }}}{dt}}\times {\vec {r}}.

В приведенном выше уравнении есть три геометрических члена ускорения на справа. Первый член «центробежного ускорения» зависит только от радиального положения r, а не от скорости нашего объекта, второй член «ускорения Кориолиса» зависит только от скорости объекта во вращающейся системе отсчета vrot но не его положение, и третий член «эйлерова ускорения» зависит только от положения и скорости изменения угловой скорости кадра.

В каждом из этих случаев физическое или собственное ускорение отличается от координатного ускорения, поскольку на последнее может влиять ваш выбор системы координат, а также физические силы, действующие на объект. Те компоненты координатного ускорения, не вызванные физическими силами (такими как прямой контакт или электростатическое притяжение), часто приписываются (как в приведенном выше ньютоновском примере) силам, которые: (i) действуют на каждую унцию объекта, (ii) вызывают массу - независимые ускорения и (iii) существуют не со всех точек зрения. К таким геометрическим (или неправильным) силам относятся силы Кориолиса, силы Эйлера, силы перегрузки, центробежные силы и (как мы видим ниже) силы тяжести.

Вид из плоского среза пространства-времени
Динамика правильного кадра в пространстве-времени (1 + 1) D.

Связь правильного ускорения с координатным ускорением в заданном срезе плоского пространства-времени вытекает из Метрическое уравнение плоского пространства Минковского (cdτ) = (cdt) - (d x ). Здесь единая система отсчета мер и синхронизированных часов определяет положение карты x и время карты t соответственно, часы движущегося объекта определяют собственное время τ, а буква «d» перед координатой означает бесконечно малое изменение. Эти отношения позволяют решать различные проблемы «инженерии любой скорости», хотя и только с точки зрения наблюдателя, чья расширенная рамка карты определяет одновременность.

Ускорение в (1 + 1) D

На этом графике показано, как космический корабль, способный на ускорение в 1 gee (10 м / с или около 1,0 светового года в квадрате) в течение 100 лет, может обеспечить поездку. практически в любую точку видимой Вселенной и обратно в течение всей жизни.

В однонаправленном случае, т.е. когда ускорение объекта параллельно или антипараллельно его скорости в пространственно-временном срезе наблюдателя, правильное ускорение α и Координатное ускорение a связано через коэффициент Лоренца γ на α=γa. Следовательно, изменение собственной скорости w = dx / dτ является интегралом собственного ускорения в течение отображаемого времени t, то есть Δw = αΔt для постоянного α. На низких скоростях это сводится к хорошо известному соотношению между координатой скоростью и координатами ускорения, умноженными на отображение времени, то есть Δv = aΔt.

Для постоянного однонаправленного собственного ускорения аналогичные отношения существуют между быстротой η и прошедшим собственным временем Δτ, а также между коэффициентом Лоренца γ и пройденным расстоянием Δx. Чтобы быть конкретным:

α = Δ вес Δ t = c Δ η Δ τ = c 2 Δ γ Δ x {\ displaystyle \ alpha = {\ frac {\ Delta w} {\ Delta t}} = c {\ frac {\ Delta \ eta} {\ Delta \ tau}} = c ^ {2} {\ frac {\ Delta \ gamma} {\ Delta x}}}\alpha ={\frac {\Delta w}{\Delta t}}=c{\frac {\Delta \eta }{\Delta \tau }}=c^{2}{\frac {\Delta \gamma }{\Delta x}},

, где различные параметры скорости связаны между собой

η знак равно sinh - 1 ⁡ (wc) = tanh - 1 ⁡ (vc) = ± cosh - 1 ⁡ (γ) {\ displaystyle \ eta = \ sinh ^ {- 1} \ left ({\ frac {w} {c }} \ right) = \ tanh ^ {- 1} \ left ({\ frac {v} {c}} \ right) = \ pm \ cosh ^ {- 1} \ left (\ gamma \ right)}\ eta = \ sinh ^ {- 1} \ left ({\ frac {w} {c}} \ right) = \ tanh ^ {- 1} \ left ({\ frac { v } {c}} \ right) = \ pm \ cosh ^ {- 1} \ left (\ gamma \ right) .

Эти уравнения описывают некоторые последствия ускоренного движения на высокой скорости. Например, представьте космический корабль, который может разгонять своих пассажиров со скоростью «1 gee» (10 м / с или около 1,0 светового года в год в квадрате) на полпути к месту назначения, а затем замедлять их со скоростью «1 gee» в течение оставшейся половины, чтобы обеспечить земную искусственную гравитацию из точки А в точку Б в кратчайшие сроки. Для расстояния по карте Δx AB первое уравнение выше предсказывает фактор Лоренца средней точки (по сравнению с его единичным значением покоя) γ mid = 1 + α (Δx AB / 2) / c. Следовательно, время приема-передачи на часах путешественника будет Δτ = 4 (c / α) ch (γ mid), в течение которого время, прошедшее на часах карты, будет Δt = 4 (c / α) sinh [ch (γ mid)].

Этот воображаемый космический корабль может совершать полеты к Проксиме Центавра продолжительностью около 7,1 лет путешествий (~ 12 лет по земным часам), туда и обратно к Млечному Пути. центральная черная дыра примерно 40 лет (~ 54 000 лет, прошедших по земным часам), и полеты туда и обратно к галактике Андромеды продолжительностью около 57 лет (более 5 миллионов лет по земным часам). К сожалению, поддерживать ускорение в 1 Ge в течение многих лет легче, чем сделать, о чем свидетельствует соотношение максимальной полезной нагрузки и стартовой массы, показанное на рисунке справа.

В искривленном пространстве-времени

На языке общей теории относительности компоненты четырехвектора A ускорения объекта (величина которого является собственным ускорением) связаны с элементами четырехскоростная через ковариантную производную D по собственному времени τ:

A λ: = DU λ d τ = d U λ d τ + Γ λ μ ν U μ U ν {\ displaystyle A ^ {\ lambda}: = {\ frac {DU ^ {\ lambda}} {d \ tau}} = {\ frac {dU ^ {\ lambda}} {d \ tau}} + \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu}}A^{\lambda }:={\frac {DU^{\lambda }}{d\tau }}={\frac {dU^{\lambda }}{d\tau }}+\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }

Здесь U - четырехскоростная объекта, а Γ - координата 64 коэффициента связи системы или символов Кристоффеля. Обратите внимание, что греческие индексы принимают четыре возможных значения, а именно 0 для оси времени и 1-3 для осей пространственных координат, и что повторяющиеся индексы используются для обозначения суммирования по всем значениям этого индекса. Траектории с нулевым собственным ускорением называются геодезическими.

Левая часть этой системы из четырех уравнений (по одному для времениподобных и трех пространственных значений индекса λ) является собственным ускорением объекта 3- вектор в сочетании с нулевым компонентом времени, если смотреть с точки зрения справочной или бухгалтерской системы координат, в которой объект находится в состоянии покоя. Первый член справа указывает скорость, с которой времяподобные (энергия / mc) и пространственные (импульс / m) компоненты четырехскоростной U объекта изменяются за единицу времени τ на часах путешественника.

Давайте решим этот первый член справа, поскольку на низких скоростях его пространственноподобные компоненты представляют собой координатное ускорение. В более общем смысле, когда первый член обращается в ноль, координатное ускорение объекта стремится к нулю. Это дает...

d U λ d τ знак равно A λ - Γ λ μ ν U μ U ν {\ displaystyle {\ frac {dU ^ {\ lambda}} {d \ tau}} = A ^ {\ lambda} - \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu}}{\frac {dU^{\lambda }}{d\tau }}=A^{\lambda }-\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }.

Таким образом, как показано на примере первых двух анимаций выше, координатное ускорение переходит в ноль, когда собственное ускорение в точности отменяется термином соединения (или геометрическим ускорением) справа. Внимание: этот член может быть суммой до шестнадцати отдельных членов, зависящих от скорости и положения, поскольку повторяющиеся индексы µ и ν по соглашению суммируются по всем парам их четырех допустимых значений.

Сила и эквивалентность

Вышеприведенное уравнение также предлагает некоторое представление о силах и принципе эквивалентности. Рассмотрим координаты локального бухгалтера для метрики (например, локальная тетрада Лоренца, подобная той, о которой глобальные системы позиционирования предоставляют информацию) для описания времени в секундах и пространства в единицах расстояния вдоль перпендикулярных осей. Если мы умножим вышеприведенное уравнение на массу покоя движущегося объекта m и разделим на коэффициент Лоренца γ = dt / dτ, пространственноподобные компоненты выразят скорость изменения количества движения для этого объекта с точки зрения координат, используемых для описания метрики.

Это, в свою очередь, может быть разбито на части из-за правильных и геометрических компонентов ускорения и силы. Если мы дополнительно умножим временную составляющую на скорость света c и определим координатную скорость как v = d x / dt, мы также получим выражение для скорости изменения энергии:

d E dt = v → ⋅ dp → dt {\ displaystyle {\ frac {dE} {dt}} = {\ vec {v}} \ cdot {\ frac {d {\ vec {p}}} {dt }}}{\frac {dE}{dt}}={\vec {v}}\cdot {\frac {d{\vec {p}}}{dt}}(подобный времени) и dp → dt = Σ fo → + Σ fg → = m (ao → + ag →) {\ displaystyle {\ frac {d {\ vec {p}) }} {dt}} = \ Sigma {\ vec {f_ {o}}} + \ Sigma {\ vec {f_ {g}}} = m ({\ vec {a_ {o}}} + {\ vec { a_ {g}}})}{\frac {d{\vec {p}}}{dt}}=\Sigma {\vec {f_{o}}}+\Sigma {\vec {f_{g}}}=m({\vec {a_{o}}}+{\vec {a_{g}}})(пробел).

Здесь a o - это ускорение, вызванное соответствующими силами, а g по умолчанию, геометрическое ускорение, которое, как мы видим, применяется к объекту из-за выбора нашей системы координат. На низких скоростях эти ускорения объединяются для создания координатного ускорения, такого как a=dx/ dt, в то время как для однонаправленного движения на любой скорости величина a o равна величине надлежащего ускорения α, как в разделе выше, где α = γa, когда a g равно нулю. В общем, выражение этих ускорений и сил может быть сложным.

Тем не менее, если мы используем эту разбивку для описания коэффициента связи (Γ) выше в терминах геометрических сил, то движение объектов с точки зрения любой системы координат (по крайней мере, на малых скоростях) может рассматриваться как локально ньютоновский. Это уже обычная практика, например. с центробежной силой и гравитацией. Таким образом, принцип эквивалентности распространяет локальную применимость законов Ньютона на ускоренные системы координат и за их пределы.

обитатели поверхности на планете

Для низкоскоростных наблюдателей, удерживаемых на фиксированном радиусе от центра сферической планеты или звезды, координатное ускорение aоболочки приблизительно соответствует собственному ускорение aoна:

a → shell = a → o - rr - rs GM r 2 r ^ {\ displaystyle {\ vec {a}} _ {shell} = {\ vec {a}} _ {o } - {\ sqrt {\ frac {r} {r-r_ {s}}}} {\ frac {GM} {r ^ {2}}} {\ hat {r}}}{\vec {a}}_{shell}={\vec {a}}_{o}-{\sqrt {\frac {r}{r-r_{s}}}}{\frac {GM}{r^{2}}}{\hat {r}}

где планета или радиус звезды по Шварцшильду rs= 2GM / c. Когда радиус нашего наблюдателя-оболочки приближается к радиусу Шварцшильда, правильное ускорение a o, необходимое для предотвращения падения, становится недопустимым.

С другой стороны, для r>>r s необходима восходящая собственная сила только GMm / r, чтобы предотвратить ускорение вниз. На поверхности Земли это выглядит следующим образом:

a → shell = a → o - gr ^ {\ displaystyle {\ vec {a}} _ {shell} = {\ vec {a}} _ {o} -g {\ hat {r}}}{\vec {a}}_{shell}={\vec {a}}_{o}-g{\hat {r}}

где g - ускорение силы тяжести вниз 9,8 м / с, а r ^ {\ displaystyle {\ hat {r}}}{\ hat {r}} - единичный вектор в радиальном направлении наружу от центра гравитирующего тела. Таким образом, здесь необходима соответствующая внешняя сила в мг, чтобы не дать человеку ускориться вниз.

Выведение четырех векторов

Пространственно-временные уравнения этого раздела позволяют учесть все отклонения между собственным и координатным ускорением в одном вычислении. Например, вычислим символы Кристоффеля :

({Γ ttt, Γ trt, Γ t θ t, Γ t ϕ t} {Γ rtt, Γ rrt, Γ r θ t, Γ r ϕ t} { Γ θ tt, Γ θ rt, Γ θ θ t, Γ θ ϕ t} {Γ ϕ tt, Γ ϕ rt, Γ ϕ θ t, Γ ϕ ϕ t} {Γ ttr, Γ trr, Γ t θ r, Γ t ϕ r} {Γ rtr, Γ rrr, Γ r θ r, Γ r ϕ r} {Γ θ tr, Γ θ rr, Γ θ θ r, Γ θ ϕ r} {Γ ϕ tr, Γ ϕ rr, Γ ϕ θ r, Γ ϕ ϕ r} {Γ tt θ, Γ tr θ, Γ t θ θ, Γ t ϕ θ} {Γ rt θ, Γ rr θ, Γ r θ θ, Γ r ϕ θ} {Γ θ t θ, Γ θ r θ, Γ θ θ θ, Γ θ ϕ θ} {Γ ϕ t θ, Γ ϕ r θ, Γ ϕ θ θ, Γ ϕ ϕ θ} {Γ tt ϕ, Γ tr ϕ, Γ t θ ϕ, Γ t ϕ ϕ} {Γ rt ϕ, Γ rr ϕ, Γ r θ ϕ, Γ r ϕ ϕ} {Γ θ t ϕ, Γ θ r ϕ, Γ θ θ ϕ, Γ θ ϕ ϕ} {Γ ϕ T ϕ, Γ ϕ r ϕ, Γ ϕ θ ϕ, Γ ϕ ϕ ϕ}) {\ displaystyle \ left ({\ begin {array} {llll} \ left \ {\ Gamma _ {tt} ^ {t}, \ Gamma _ {tr} ^ {t}, \ Gamma _ {t \ theta} ^ {t}, \ Gamma _ {t \ phi} ^ {t} \ right \} \ left \ {\ Gamma _ {rt } ^ {t}, \ Gamma _ {rr} ^ {t}, \ Gamma _ {r \ theta} ^ {t}, \ Gamma _ {r \ phi} ^ {t} \ right \} и \ left \ {\ Gamma _ {\ theta t} ^ {t}, \ Gamm a _ {\ theta r} ^ {t}, \ Gamma _ {\ theta \ theta} ^ {t}, \ Gamma _ {\ theta \ phi} ^ {t} \ right \} и \ left \ {\ Gamma _ {\ phi t} ^ {t}, \ Gamma _ {\ phi r} ^ {t}, \ Gamma _ {\ phi \ theta} ^ {t}, \ Gamma _ {\ phi \ phi} ^ {t } \ right \} \\\ left \ {\ Gamma _ {tt} ^ {r}, \ Gamma _ {tr} ^ {r}, \ Gamma _ {t \ theta} ^ {r}, \ Gamma _ { t \ phi} ^ {r} \ right \} \ left \ {\ Gamma _ {rt} ^ {r}, \ Gamma _ {rr} ^ {r}, \ Gamma _ {r \ theta} ^ {r }, \ Gamma _ {r \ phi} ^ {r} \ right \} \ left \ {\ Gamma _ {\ theta t} ^ {r}, \ Gamma _ {\ theta r} ^ {r}, \ Гамма _ {\ theta \ theta} ^ {r}, \ Gamma _ {\ theta \ phi} ^ {r} \ right \} и \ left \ {\ Gamma _ {\ phi t} ^ {r}, \ Gamma _ {\ phi r} ^ {r}, \ Gamma _ {\ phi \ theta} ^ {r}, \ Gamma _ {\ phi \ phi} ^ {r} \ right \} \\\ left \ {\ Gamma _ {tt} ^ {\ theta}, \ Gamma _ {tr} ^ {\ theta}, \ Gamma _ {t \ theta} ^ {\ theta}, \ Gamma _ {t \ phi} ^ {\ theta} \ right \} \ left \ {\ Gamma _ {rt} ^ {\ theta}, \ Gamma _ {rr} ^ {\ theta}, \ Gamma _ {r \ theta} ^ {\ theta}, \ Gamma _ { r \ phi} ^ {\ theta} \ right \} \ left \ {\ Gamma _ {\ theta t} ^ {\ theta}, \ Gamma _ {\ theta r} ^ {\ theta}, \ Gamma _ { \ theta \ theta} ^ {\ theta}, \ Gamma _ {\ theta \ phi} ^ {\ theta} \ right \} и \ left \ {\ Gamma _ {\ phi t} ^ {\ theta}, \ Gamma _ {\ phi r} ^ {\ theta}, \ Gamma _ {\ phi \ theta} ^ {\ theta}, \ Gamma _ {\ phi \ phi} ^ {\ theta } \ right \} \\\ left \ {\ Gamma _ {tt} ^ {\ phi}, \ Gamma _ {tr} ^ {\ phi}, \ Gamma _ {t \ theta} ^ {\ phi}, \ Гамма _ {t \ phi} ^ {\ phi} \ right \} и \ left \ {\ Gamma _ {rt} ^ {\ phi}, \ Gamma _ {rr} ^ {\ phi}, \ Gamma _ {r \ theta} ^ {\ phi}, \ Gamma _ {r \ phi} ^ {\ phi} \ right \} и \ left \ {\ Gamma _ {\ theta t} ^ {\ phi}, \ Gamma _ {\ theta r} ^ {\ phi}, \ Gamma _ {\ theta \ theta} ^ {\ phi}, \ Gamma _ {\ theta \ phi} ^ {\ phi} \ right \} и \ left \ {\ Gamma _ {\ phi t} ^ {\ phi}, \ Gamma _ {\ phi r} ^ {\ phi}, \ Gamma _ {\ phi \ theta} ^ {\ phi}, \ Gamma _ {\ phi \ phi} ^ {\ phi} \ right \} \ end {array}} \ right)}\ left ({\ begin {array} {llll} \ left \ {\ Gamma _ {tt} ^ {t}, \ Gamma _ {tr} ^ {t}, \ Gamma _ {t \ theta} ^ {t}, \ Gamma _ {t \ phi} ^ {t} \ right \} \ left \ {\ Gamma _ {rt } ^ {t}, \ Gamma _ {rr} ^ {t}, \ Gamma _ {r \ theta} ^ {t}, \ Gamma _ {r \ phi} ^ {t} \ right \} и \ left \ {\ Gamma _ {\ theta t} ^ {t}, \ Gamma _ {\ theta r} ^ {t}, \ Gamma _ {\ theta \ theta} ^ {t}, \ Gamma _ {\ theta \ phi} ^ {t} \ right \} \ left \ {\ Gamma _ {\ phi t} ^ {t}, \ Gamma _ {\ phi r} ^ {t}, \ Gamma _ {\ phi \ theta} ^ { t}, \ Gamma _ {\ phi \ phi} ^ {t} \ right \} \\\ left \ {\ Gamma _ {tt} ^ {r}, \ Gamma _ {tr} ^ {r}, \ Gamma _ {t \ theta} ^ {r}, \ Gamma _ {t \ phi} ^ {r} \ right \} \ left \ {\ Gamma _ {rt} ^ {r}, \ Gamma _ {rr} ^ {r}, \ Gamma _ {r \ theta} ^ {r}, \ Gamma _ {r \ phi} ^ {r} \ right \} \ left \ {\ Gamma _ {\ theta t} ^ {r}, \ Gamma _ {\ theta r} ^ {r}, \ Gamma _ {\ theta \ theta} ^ {r}, \ Gamma _ {\ theta \ phi} ^ {r} \ right \} и \ left \ { \ Gamma _ {\ phi t} ^ {r}, \ Gamma _ {\ phi r} ^ {r}, \ Gamma _ {\ phi \ theta} ^ {r}, \ Gamma _ {\ phi \ phi} ^ {r} \ right \} \\\ left \ {\ Gamma _ {tt} ^ {\ theta}, \ Gamma _ {tr} ^ {\ theta}, \ Gamma _ {t \ theta} ^ {\ theta}, \ Gamma _ {t \ phi} ^ {\ theta} \ right \} \ слева \ {\ Gamma _ {rt} ^ {\ theta}, \ Gamma _ {rr} ^ {\ theta}, \ Gamma _ {r \ theta} ^ {\ theta}, \ Gamma _ {r \ phi} ^ {\ theta} \ right \} \ left \ {\ Gamma _ {\ theta t} ^ {\ theta}, \ Gamma _ {\ theta r} ^ {\ theta}, \ Gamma _ {\ theta \ theta} ^ {\ theta}, \ Gamma _ {\ theta \ phi} ^ {\ theta} \ right \} и \ left \ {\ Gamma _ {\ phi t }^{\theta },\Gamma _{\phi r}^{\theta },\Gamma _{\phi \theta }^{\theta },\Gamma _{\phi \phi }^{\theta }\right\}\\\left\{\Gamma _{tt}^{\phi },\Gamma _{tr}^{\phi },\Gamma _{t\theta }^{\phi },\Gamma _{t\phi }^{\phi }\right\}\left\{\Gamma _{rt}^{\phi },\Gamma _{rr}^{\phi },\Gamma _{r\theta }^{\phi },\Gamma _{r\phi }^{\phi }\right\}\left\{\Gamma _{\theta t}^{\phi },\Gamma _{\theta r}^{\phi },\Gamma _{\theta \theta }^{\phi },\Gamma _{\theta \phi }^{\phi }\right\}\left\{\Gamma _{\phi t}^{\phi },\Gamma _{\phi r}^{\phi },\Gamma _{\phi \theta }^{\phi },\Gamma _{\phi \phi }^{\phi }\right\}\end{array}}\right)

для дальней координаты метрики Шварцшильда (c dτ) = (1 − r s / r) (c dt) - (1 / (1 − r s / r)) dr - r dθ - (r sinθ) dφ, где r s - Радиус Шварцшильда 2GM / c. Результирующий массив коэффициентов принимает следующий вид:

({0, rs 2 r (r - rs), 0, 0} {rs 2 r (r - rs), 0, 0, 0} {0, 0, 0, 0} {0, 0, 0, 0} {rsc 2 (r - rs) 2 r 3, 0, 0, 0} {0, rs 2 r (rs - r), 0, 0} {0, 0, rs - r, 0} {0, 0, 0, (rs - r) sin 2 ⁡ θ} {0, 0, 0, 0} {0, 0, 1 r, 0} {0, 1 r, 0, 0} {0, 0, 0, - cos ⁡ θ sin ⁡ θ} {0, 0, 0, 0} {0, 0, 0, 1 r} {0, 0, 0, cot ⁡ (θ)} { 0, 1 р, детская кроватка ⁡ θ, 0}) {\ displaystyle \ left ({\ begin {array} {llll} \ left \ {0, {\ frac {r_ {s}}} {2r (r-r_ {s) })}}, 0,0 \ right \} и \ left \ {{\ frac {r_ {s}} {2r (r-r_ {s})}}, 0,0,0 \ right \} \ {0,0,0,0 \} \ {0,0,0,0 \} \\\ left \ {{\ frac {r_ {s} c ^ {2} (r-r_ {s})} {2r ^ {3}}}, 0,0,0 \ right \} и \ left \ {0, {\ frac {r_ {s}} {2r (r_ {s} -r)}}, 0,0 \ right \} \ {0,0, r_ {s} -r, 0 \} \ left \ {0,0,0, (r_ {s} -r) \ sin ^ {2} \ theta \ right \} \\\ {0,0,0,0 \} \ left \ {0,0, {\ frac {1} {r}}, 0 \ right \} и \ left \ {0, {\ frac {1} {r}}, 0,0 \ right \} \ {0,0,0, - \ cos \ theta \ sin \ theta \} \\\ {0,0,0,0 \} \ влево \ {0,0,0, {\ frac {1} {r}} \ right \} \ {0, 0,0, \ cot (\ theta) \} \ left \ {0, {\ frac {1} {r}}, \ cot \ theta, 0 \ right \} \ end {array}} \ right)}\left({\begin{array}{llll}\left\{0,{\frac {r_{s}}{2r(r-r_{s})}},0,0\right\}\left\{{\frac {r_{s}}{2r(r-r_{s})}},0,0,0\right\}\{0,0,0,0\}\{0,0,0,0\}\\\left\{{\frac {r_{s}c^{2}(r-r_{s})}{2r^{3}}},0,0,0\right\}\left\{0,{\frac {r_{s}}{2r(r_{s}-r)}},0,0\right\}\{0,0,r_{s}-r,0\}\left\{0,0,0,(r_{s}-r)\sin ^{2}\theta \right\}\\\{0,0,0,0\}\left\{0,0,{\frac {1}{r}},0\right\}\left\{0,{\frac {1}{r}},0,0\right\}\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}\left\{0,0,0,{\frac {1}{r}}\right\}\{0,0,0,\cot(\theta)\}\left\{0,{\frac {1}{r}},\cot \theta,0\right\}\end{array}}\right).

Отсюда вы можете получить правильное ускорение рамы оболочки, установив координатное ускорение на ноль и, таким образом, требуя, чтобы правильное ускорение нейтрализовало геометрическое ускорение неподвижного объекта, т.е. A λ = Γ λ μ ν U μ U ν = {0, GM / r 2, 0, 0} {\ displaystyle A ^ {\ lambda} = \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu} = \ {0, GM / r ^ {2}, 0,0 \}}A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,GM/r^{2},0,0\}. Это еще не решает проблему, поскольку координаты Шварцшильда в искривленном пространстве-времени являются координатами бухгалтера, а не координатами местного наблюдателя. Величина указанного выше 4-вектора правильного ускорения, а именно α = 1 / (1 - rs / r) GM / r 2 {\ displaystyle \ alpha = {\ sqrt {1 / (1-r_ {s} / r)}} GM / r ^ {2}}\alpha ={\sqrt {1/(1-r_{s}/r)}}GM/r^{2}, однако это именно то, что мы хотим, то есть правильное ускорение, инвариантное к системе отсчета вверх, необходимое для противодействия геометрическому ускорению вниз, ощущаемому обитателями поверхности планеты.

Особым случаем вышеупомянутого набора символов Кристоффеля является набор плоских пространств сферических координат, полученных путем установки r s или M выше нуля:

( {0, 0, 0, 0} {0, 0, 0, 0} {0, 0, 0, 0} {0, 0, 0, 0} {0, 0, 0, 0} {0, 0, 0, 0} {0, 0, - r, 0} {0, 0, 0, - r sin 2 ⁡ θ} {0, 0, 0, 0} {0, 0, 1 r, 0} {0, 1 r, 0, 0} {0, 0, 0, - cos ⁡ θ sin ⁡ θ} {0, 0, 0, 0} {0, 0, 0, 1 r} {0, 0, 0, детская кроватка ⁡ θ} {0, 1 р, детская кроватка ⁡ θ, 0}) {\ displaystyle \ left ({\ begin {array} {llll} \ left \ {0,0,0,0 \ right \} \ left \ { 0,0,0,0 \ right \} \ {0,0,0,0 \} \ {0,0,0,0 \} \\\ left \ {0,0,0,0 \ right \} \ left \ {0,0,0,0 \ right \} \ {0,0, -r, 0 \} \ left \ {0,0,0, -r \ sin ^ {2} \ theta \ right \} \\\ {0,0,0,0 \} \ left \ {0,0, {\ frac {1} {r}}, 0 \ right \} и \ left \ {0, {\ frac {1} {r}}, 0,0 \ right \} \ {0,0,0, - \ cos \ theta \ sin \ theta \} \\\ {0,0,0,0 \} \ left \ {0,0,0, {\ frac {1} {r}} \ right \} \ {0,0,0, \ cot \ theta \} \ left \ {0, { \ frac {1} {r}}, \ cot \ theta, 0 \ right \} \ end {array}} \ right)}\left({\begin{array}{llll}\left\{0,0,0,0\right\}\left\{0,0,0,0\right\}\{0,0,0,0\}\{0,0,0,0\}\\\left\{0,0,0,0\right\}\left\{0,0,0,0\right\}\{0,0,-r,0\}\left\{0,0,0,-r\sin ^{2}\theta \right\}\\\{0,0,0,0\}\left\{0,0,{\frac {1}{r}},0\right\}\left\{0,{\frac {1}{r}},0,0\right\}\{0,0,0,-\cos \theta \sin \theta \}\\\{0,0,0,0\}\left\{0,0,0,{\frac {1}{r}}\right\}\{0,0,0,\cot \theta \}\left\{0,{\frac {1}{r}},\cot \theta,0\right\}\end{array}}\right).

Отсюда мы c и получить, например, собственное центростремительное ускорение, необходимое для компенсации центробежного геометрического ускорения объекта, движущегося с постоянной угловой скоростью ω = dφ / dτ на экваторе, где θ = π / 2. Формирование той же 4-векторной суммы, что и выше для случая dθ / dτ и dr / dτ нуля, дает не что иное, как классическое ускорение для вращательного движения, данное выше, то есть A λ = Γ λ μ ν U μ U ν = {0, - р (d ϕ / d τ) 2, 0, 0} {\ displaystyle A ^ {\ lambda} = \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu} = \ {0, -r (d \ phi / d \ tau) ^ {2}, 0,0 \}}A^{\lambda }=\Gamma ^{\lambda }{}_{\mu \nu }U^{\mu }U^{\nu }=\{0,-r(d\phi /d\tau)^{2},0,0\}, так что o = ωr. Эффекты Кориолиса также находятся в этих коэффициентах связи и аналогичным образом возникают только из геометрии системы координат.

См. Также
Сноски
Внешние ссылки
Последняя правка сделана 2021-06-02 08:15:01
Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное).
Обратная связь: support@alphapedia.ru
Соглашение
О проекте