| Равномерная n-угольная антипризма | |
|---|---|
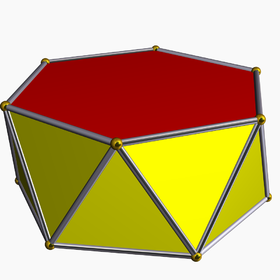 . Пример гексагональной антипризмы . Пример гексагональной антипризмы | |
| Тип | равномерная в смысле полуправильный многогранник |
| Грани | 2 n-угольники, 2n треугольники |
| ребра | 4n |
| вершины | 2n |
| Обозначение многогранника Конвея | An |
| Конфигурация вершины | 3.3.3.n |
| символ Шлефли | {} ⊗ {n}. s {2,2n}. sr {2, n} |
| Диаграммы Кокстера | |
| Группа симметрии | Dnd, [2,2n], (2 * n), порядок 4n |
| Группа вращения | Dn, [2, n], (22n), порядок 2n |
| Двойной многогранник | выпуклый двойственно-однородный n-угольный трапецоэдр |
| Свойства | выпуклый, vertex-t ransitive, правильный многоугольник грани |
| Net |  |
В геометрии, n-угольная антипризма или n-сторонняя антипризма - это многогранник, состоящий из двух параллельных копий некоторого конкретного n-стороннего многоугольника, соединенных чередующейся лентой из треугольников. Антипризмы являются подклассом призматоидов и (вырожденным) типом курносых многогранников.
Антипризмы похожи на призмы за исключением того, что основания скручены относительно друг друга, и что боковые грани представляют собой треугольники, а не четырехугольники.
В случае обычной n-сторонней основы обычно рассматривают случай, когда ее копия скручена на угол 180 / n градусов. Дополнительная регулярность достигается, когда линия, соединяющая центры основания, перпендикулярна плоскостям основания, что делает ее правой антипризмой . В качестве граней он имеет два n-угольных основания и, соединяя эти основания, 2n равнобедренных треугольников.
A равномерная антипризма имеет, помимо основных граней, 2n равносторонних треугольников в качестве граней. Равномерные антипризмы образуют бесконечный класс вершинно-транзитивных многогранников, как и равномерные призмы. Для n = 2 у нас есть правильный тетраэдр как двуугольная антипризма (вырожденная антипризма), а для n = 3 правильный октаэдр как треугольная антипризма (невырожденная антипризма).
Двойные многогранники антипризм - это трапеции. Их существование обсуждалось, и их имя было придумано Иоганном Кеплером, хотя возможно, что они были ранее известны Архимеду, поскольку они удовлетворяют тем же условиям на вершинах, что и Архимедовы тела.
Семейство однородных n-угольных антипризм [
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника | ... | Апейрогональная антипризма | ||||||||||||
| Сферическое мозаичное изображение | Плоское мозаичное изображение | |||||||||||||
| Вершина конфигурация n.3.3.3 | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3. 3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ... | ∞.3.3.3 | |
| .... A3 |  . A4 . A4 |  . A5 . A5 |  . A6 . A6 |  . A7 . A7 |  . A8 . A8 |
Декартовы координаты для вершин правой антипризмы с (правильными) n-угольными основаниями и равнобедренными треугольниками равны

с k в диапазоне от 0 до 2n - 1; если треугольники равносторонние,

Пусть a будет длиной ребра однородной антипризмы. Тогда объем равен

и площадь поверхности равна

Существует бесконечный набор усеченных антипризм, включая форму усеченного октаэдра с более низкой симметрией (усеченная треугольная антипризма). Их можно чередовать для создания курносых антипризм, две из которых являются твердыми телами Джонсона, а курносая треугольная антипризма представляет собой форму икосаэдра с более низкой симметрией..
| Антипризмы | ||||
|---|---|---|---|---|
 |  |  |  | ... |
| с {2,4} | с {2,6} | с {2,8} | с {2,10} | с {2,2n} |
| Усеченные антипризмы | ||||
 |  |  |  | ... |
| ц {2,4} | ц {2,6} | ц {2,8} | ц {2,10} | ts {2,2n} |
| Курносые антипризмы | ||||
| J84 | Икосаэдр | J85 | Неровные грани... | |
 |  |  | ... | |
| ss {2,4} | ss {2,6} | ss {2,8} | ss {2,10} | ss {2,2n} |
Симметрия группа правой n-сторонней антипризмы с правильным основанием и равнобедренными боковыми гранями - D nd порядка 4n, за исключением случая тетраэдра , имеющего большую симметрию группа T d порядка 24, которая имеет три версии D 2d в качестве подгрупп, и октаэдр, который имеет большую группу симметрии O h порядка 48, который имеет четыре версии D 3d в качестве подгрупп.
Группа симметрии содержит inversion тогда и только тогда, когда n нечетно.
группа вращения - это D n порядка 2n, за исключением случая тетраэдра, который имеет большую группу вращения T порядка 12, который имеет три версии D 2 в качестве подгрупп и октаэдр, который имеет большую группу вращения O порядка 24, который имеет четыре версии D 3 в качестве подгрупп.
 . 5/2-антипризма . 5/2-антипризма | 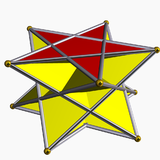 . 5/3-антипризма . 5/3-антипризма | ||||
 . 9/2-антипризма . 9/2-антипризма |  . 9/4-антипризма . 9/4-антипризма |  . 9/5-антипризма . 9/5-антипризма | |||
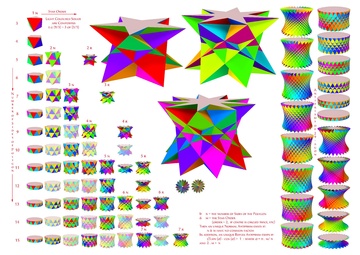 Здесь показаны все антипризмы, не являющиеся звездой, и звездные антипризмы с точностью до 15 сторон - вместе со сторонами икосикаеннагона.
Здесь показаны все антипризмы, не являющиеся звездой, и звездные антипризмы с точностью до 15 сторон - вместе со сторонами икосикаеннагона. Однородные звездные антипризмы названы по их основаниям звездного многоугольника, {p / q} и существуют в прямом и ретроградном (скрещенном) решениях. Скрещенные формы имеют пересекающиеся фигуры вершин и обозначаются перевернутыми дробями, p / (p - q) вместо p / q, например 5/3 вместо 5/2.
В ретроградных формах, но не в прямолинейных, треугольники, соединяющие основания звезд, пересекают ось вращательной симметрии.
Некоторые ретроградные звездные антипризмы с правильными выпуклыми основаниями многоугольника не могут быть построены с равными длинами ребер, поэтому они не являются однородными многогранниками.
Соединения звездчатой антипризмы также могут быть построены, где p и q имеют общие множители; Пример: звездная антипризма 10/4 представляет собой соединение двух звездчатых антипризм 5/2.
| Звездные антипризмы по симметрии, до 12 | |||||
|---|---|---|---|---|---|
| Группа симметрии | Однородные звезды | Другие звезды | |||
| D4d. [2,8]. (2 * 5) |  . 3.3 / 2.3.4 . 3.3 / 2.3.4 | ||||
| D5h. [2,5]. (* 225) |  . 3.3.3.5/2 . 3.3.3.5/2 |  . 3.3 / 2.3.5 . 3.3 / 2.3.5 | |||
| D5d. [2,10]. (2 * 5) |  . 3.3.3.5/3 . 3.3.3.5/3 | ||||
| D6d. [2,12]. (2 * 6) | 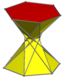 . 3.3 / 2.3.6 . 3.3 / 2.3.6 | ||||
| D7h. [2,7]. (* 227) |  . 3.3.3.7/2 . 3.3.3.7/2 |  . 3.3.3.7/4 . 3.3.3.7/4 | |||
| D7d. [2,14]. (2 * 7) |  . 3.3.3.7/3 . 3.3.3.7/3 | ||||
| D8d. [2,16]. (2 * 8) |  . 3.3.3.8/3 . 3.3.3.8/3 |  . 3.3.3.8/5 . 3.3.3.8/5 | |||
| D9h. [2,9]. (* 229) |  . 3.3.3.9/2 . 3.3.3.9/2 |  . 3.3.3.9/4 . 3.3.3.9/4 | |||
| D9d. [2,18]. (2 * 9) |  . 3.3.3.9/5 . 3.3.3.9/5 | ||||
| D10d. [2,12]. (2 * 10) |  . 3.3.3.10/3 . 3.3.3.10/3 | ||||
| D11h. [2,11]. (* 2.2.11) |  . 3.3.3.11/2 . 3.3.3.11/2 |  . 3.3.3.11/4 . 3.3.3.11/4 |  . 3.3. 3.11 / 6 . 3.3. 3.11 / 6 | ||
| D11d. [2,22]. (2 * 11) |  . 3.3.3.11/3 . 3.3.3.11/3 |  . 3.3.3.11/5 . 3.3.3.11/5 |  . 3.3.3.11/7 . 3.3.3.11/7 | ||
| D12d. [2,24]. (2 * 12) |  . 3.3.3.12/5 . 3.3.3.12/5 |  . 3.3.3.12/7 . 3.3.3.12/7 | |||
| ... | |||||
| На Викискладе есть материалы, связанные с Антипризма. |