Фазовая автоподстройка частоты

Простейшая аналоговая фазовая автоподстройка частоты

A фазовая автоподстройка частоты или фазовая автоподстройка частоты (PLL ) - это система управления , которая генерирует выходной сигнал, фаза которого связана с фазой входного сигнала. Есть несколько разных типов; Самым простым является электронная схема, состоящая из генератора переменной частоты и фазового детектора в контуре обратной связи. Генератор генерирует периодический сигнал, и фазовый детектор сравнивает фазу этого сигнала с фазой входного периодического сигнала, регулируя генератор так, чтобы фазы совпадали.

Сохранение фазы входа и выхода в синхронном режиме также подразумевает сохранение одинаковых входных и выходных частот. Следовательно, в дополнение к синхронизирующим сигналам, контур фазовой автоподстройки частоты может отслеживать входную частоту или генерировать частоту, кратную входной частоте. Эти свойства используются для синхронизации часов компьютера, демодуляции и синтеза частоты.

Контуры фазовой автоподстройки частоты широко используются в радио, телекоммуникациях, компьютеры и другие электронные приложения. Их можно использовать для демодуляции сигнала, восстановления сигнала из зашумленного канала связи, генерации стабильной частоты, кратной входной частоте (синтез частоты ), или распределения точно синхронизированных часов. импульсы в цифровых логических схемах, таких как микропроцессоры. Поскольку одна интегральная схема может обеспечить полный строительный блок системы фазовой автоподстройки частоты, этот метод широко используется в современных электронных устройствах с выходными частотами от долей герца до многих гигагерц.

• 1 Практические аналогии
  • 1.1 Аналогия с автомобильной гонкой
  • 1.2 Аналогия с часами
• 2 История
• 3 Структура и функции
  • 3.1 Варианты
  • 3.2 Рабочие параметры
• 4 Приложения
  • 4.1 Восстановление тактовой частоты
  • 4.2 Выравнивание
  • 4.3 Генерация тактовой частоты
  • 4.4 Расширенный спектр
  • 4.5 Распределение тактовой частоты
  • 4.6 Обнаружение AM
  • 4.7 Снижение джиттера и шума
  • 4.8 Синтез частоты
• 5 Блок-схема
• 6 элементов
  • 6.1 Фазовый детектор
  • 6.2 Фильтр
  • 6.3 Генератор
  • 6.4 Путь обратной связи и дополнительный делитель
• 7 Моделирование
  • 7.1 Модель APLL во временной области
  • 7.2 Модель APLL в фазовой области
    • 7.2.1 Пример
  • 7.3 Линеаризованная модель в фазовой области
  • 7.4 Реализация цифровой схемы фазовой автоподстройки частоты в программном обеспечении
• 8 См. Также
• 9 Примечания
• 10 Ссылки
• 11 Дополнительная литература
• 12 Внешние ссылки

Аналогия с автомобильной гонкой

В качестве аналогии с PLL рассмотрим гонку между двумя автомобилями. Один представляет входную частоту, другой - выходную частоту генератора, управляемого напряжением (ГУН) системы ФАПЧ. Каждый круг соответствует полному циклу. Количество кругов в час (скорость) соответствует частоте. Разделение вагонов (расстояние) соответствует разности фаз между двумя колебательными сигналами.

В течение большей части гонки каждая машина сама по себе и может обгонять другую и наезжать на другую. Это аналог ФАПЧ в разблокированном состоянии.

Однако в случае аварии поднимается желтый предупреждающий флажок. Это означает, что ни одной из гоночных машин не разрешается обгонять и обгонять другую машину. Два гоночных автомобиля представляют входную и выходную частоты ФАПЧ в заблокированном состоянии. Каждый гонщик измеряет разность фаз (часть расстояния на круге) между собой и другим гоночным автомобилем. Если задний водитель находится слишком далеко, он увеличит скорость, чтобы сократить разрыв. Если они окажутся слишком близко к другой машине, водитель замедлит скорость. В результате оба гоночных автомобиля будут двигаться по трассе синхронно с фиксированной разностью фаз (или постоянным расстоянием) между ними. Поскольку ни одной машине не разрешается проехать на круге другой, машины делают одинаковое количество кругов за заданный период времени. Следовательно, частота двух сигналов одинакова.

Аналогия с часами

Фаза может быть пропорциональна времени, поэтому разность фаз может быть разницей во времени. Часы с разной степенью точности синхронизируются по фазе (с синхронизацией по времени) с ведущими часами.

Оставленные сами по себе, каждые часы будут отсчитывать время с немного разной скоростью. Настенные часы, например, могут быть быстрее на несколько секунд в час по сравнению с эталонными часами в NIST. Со временем эта разница во времени станет значительной.

Чтобы настенные часы синхронизировались с эталонными часами, каждую неделю владелец сравнивает время на своих настенных часах с более точными часами (сравнение фаз) и сбрасывает свои часы. Оставленные в покое, настенные часы будут продолжать отклоняться от эталонных часов с той же скоростью несколько секунд в час.

Некоторые часы имеют временную регулировку (быстро-медленно). Когда владелец сравнил время своих настенных часов с эталонным временем, они заметили, что их часы были слишком быстрыми. Следовательно, владелец может немного повернуть синхронизацию, чтобы часы работали немного медленнее (частота). Если все будет хорошо, их часы будут более точными, чем раньше. После серии еженедельных корректировок значение секунды для настенных часов будет совпадать с эталонным временем (зафиксированным как по частоте, так и по фазе в пределах стабильности настенных часов).

Ранняя электромеханическая версия петли фазовой автоподстройки частоты использовалась в 1921 году в часах Shortt-Synchronome.

Самопроизвольная синхронизация слабосвязанных маятниковые часы были отмечены голландским физиком Христианом Гюйгенсом еще в 1673 году. Примерно на рубеже 19 века лорд Рэлей наблюдал синхронизацию слабосвязанных органных труб. и камертоны. В 1919 году У. Х. Экклс и Дж. Х. Винсент обнаружили, что два электронных генератора, которые были настроены на колебания на несколько разных частотах, но которые были связаны с резонансным контуром, вскоре будут колебаться на той же частоте. Автоматическая синхронизация электронных генераторов была описана в 1923 году Эдвардом Виктором Эпплтоном.

. В 1925 году профессор Дэвид Робертсон, первый профессор электротехники в Бристольском университете, представил фазовую синхронизацию в своей конструкции часов. Управляйте ударами в колокол Великий Георгий в новом Мемориальном здании Уиллса. Часы Робертсона включали в себя электромеханическое устройство, которое могло изменять частоту колебаний маятника, и получали сигналы коррекции от схемы, которая сравнивала фазу маятника с фазой входящего телеграфного импульса из Гринвичской обсерватории каждое утро в 10.00 по Гринвичу. Помимо включения эквивалентов каждого элемента современной электронной ФАПЧ, система Робертсона примечательна тем, что ее фазовый детектор представлял собой релейную логическую реализацию фазово-частотного детектора, которую не видели в электронных схемах до 1970-х годов. Работа Робертсона предшествовала исследованию того, что позже было названо петлей фазовой синхронизации в 1932 году, когда британские исследователи разработали альтернативу супергетеродинному приемнику Эдвина Армстронга, Homodyne <107.>или приемник прямого преобразования. В гомодинной или синхродинной системе гетеродин настраивался на желаемую входную частоту и умножался на входной сигнал. Результирующий выходной сигнал включает исходную информацию о модуляции. Намерение состояло в том, чтобы разработать альтернативную схему приемника, которая требовала бы меньшего количества настраиваемых схем, чем супергетеродинный приемник. Поскольку частота гетеродина быстро изменялась, на генератор подавался сигнал автоматической коррекции, поддерживая его на той же фазе и частоте, что и полезный сигнал. Этот метод был описан в 1932 году в статье Анри де Беллескиза во французском журнале L'Onde Électrique.

В аналоговых телевизионных приемниках, по крайней мере, с конца 1930-х годов, используется фазовая автоподстройка частоты с горизонтальной и вертикальной разверткой. схемы привязаны к импульсам синхронизации в широковещательном сигнале.

ON Semiconductor HC4046A

Когда Signetics представила линейку монолитных интегральных схем, таких как NE565, которые были завершены Системы фазовой автоподстройки частоты на микросхеме в 1969 году, количество применений этой техники увеличилось. Несколько лет спустя RCA представила микросхему "CD4046 " CMOS Micropower Phase-Lock Loop, которая стала популярной интегральной схемой.

Механизмы фазовой автоподстройки частоты могут быть реализованы как аналоговые, так и цифровые схемы. Обе реализации используют одну и ту же базовую структуру. Аналоговые схемы ФАПЧ включают четыре основных элемента:

• фазовый детектор,
• фильтр нижних частот,
• генератор, управляемый напряжением, и
• тракт обратной связи (который может включать делитель частоты ).

Варианты

Существует несколько разновидностей схем ФАПЧ. Некоторые используемые термины включают аналоговый контур фазовой автоподстройки частоты (APLL), также называемый линейной фазовой автоподстройкой частоты (LPLL), цифровой контур фазовой автоподстройки частоты ( DPLL), полностью цифровой контур фазовой автоподстройки частоты (ADPLL) и программный контур фазовой автоподстройки частоты (SPLL).

Аналоговая или линейная система ФАПЧ (APLL)

Фазовый детектор является аналоговым умножителем. Активен контурный фильтр. или пассивный. Использует генератор, управляемый напряжением (VCO). APLL называется типом II, если его контурный фильтр имеет передаточную функцию с ровно одним полюсом в начале координат (см. также гипотезу Игана о диапазон втягивания типа II APLL ).

Цифровая ФАПЧ (DPLL)

Аналоговая ФАПЧ с цифровым фазовым детектором (например, XOR, JK-синхронизатор, фазово-частотный детектор). Может иметь цифровой делитель. в

Все цифровые схемы ФАПЧ (ADPLL)

Фазовый детектор, фильтр и генератор являются цифровыми. Использует осциллятор с числовым управлением (NCO).

Программная ФАПЧ (SPLL)

Функциональные блоки реализуются программно, а не специализированным оборудованием.

Нейронные каналы PLL (NPLL)

Фазовый детектор, фильтр и генератор - это нейроны или небольшие нейрональные пулы. Использует (RCO). Используется для отслеживания и декодирования низкочастотных модуляций (< 1 kHz), such as those occurring during mammalian-like active sensing.

ФАПЧ с зарядовой накачкой (CP-PLL)

CP-PLL - это модификация контуров фазовой автоподстройки частоты с фазочастотным детектором и сигналами прямоугольной формы. См. Также Гипотеза Гарднера о CP-PLL.

Рабочие параметры

• Тип и порядок.
• Частотные диапазоны : диапазон удержания (диапазон отслеживания), диапазон втягивания (диапазон захвата, диапазон захвата), синхронизация- См. также проблему Гарднера о диапазоне захвата, гипотезу Игана о диапазоне втягивания типа II APLL.
• Полоса пропускания контура: определение скорости контура управления.
• Переходный процесс: как выброс и время установления с определенной точностью (например, 50 ppm).
• Устойчивые ошибки: как остаточная фаза или ошибка синхронизации.
• Чистота выходного спектра : Подобно боковым полосам, генерируемым определенной пульсацией напряжения настройки ГУН.
• Фазовый шум: Определяется энергией шума в определенной полосе частот (например, смещение 10 кГц от несущей). Сильно зависит от фазы ГУН. шум, полоса пропускания ФАПЧ и т. д.
• Общие параметры: такие как потребляемая мощность, диапазон напряжения питания, выходная амплитуда и т. д.

Контуры фазовой автоподстройки частоты широко используются для синхронизация целей; в пространстве связь для когерентной демодуляции и расширения порога, битовой синхронизации и символьной синхронизации. Контуры фазовой автоподстройки частоты также могут использоваться для демодуляции частотно-модулированных сигналов. В радиопередатчиках, ФАПЧ используются для синтеза новых частот, которые кратны опорной частоты, с той же стабильностью, как и опорной частота.

Другие приложения включают в себя

• Демодуляция из частотная модуляция (FM): если система ФАПЧ привязана к FM-сигналу, ГУН отслеживает мгновенную частоту входного сигнала. Отфильтрованное напряжение ошибки, которое управляет ГУН и поддерживает синхронизацию с входным сигналом, является демодулированным выходным FM. Характеристики передачи VCO определяют линейность демодулированного выхода. Поскольку ГУН, используемый в интегральной схеме ФАПЧ, имеет высокую линейность, можно реализовать высоколинейные FM-демодуляторы.
• Демодуляция частотной манипуляции (FSK): при передаче цифровых данных и компьютерная периферия, двоичные данные передаются с помощью несущей частоты, которая сдвигается между двумя заданными частотами.
• Восстановление слабых сигналов, которые в противном случае были бы потеряны из-за шума (синхронный усилитель для отслеживания эталонной частоты)
• Восстановление информации о тактовой частоте из потока данных, например с дискового накопителя
• Умножители тактовой частоты в микропроцессорах, которые позволяют использовать внутренний процессор элементы работают быстрее, чем внешние соединения, при сохранении точных временных соотношений
• Демодуляция модемов и других тональных сигналов для телекоммуникаций и дистанционного управления.
• DSP из видеосигналов ; Контуры фазовой автоподстройки частоты также используются для синхронизации фазы и частоты с входным аналоговым видеосигналом, поэтому он может быть дискретизирован и подвергнут цифровой обработке
• Атомно-силовая микроскопия в режим частотной модуляции для обнаружения изменений резонансной частоты кантилевера из-за взаимодействий между наконечником и поверхностью
• двигатель постоянного тока привод

Восстановление часов

Некоторые потоки данных, особенно потоки высокоскоростных последовательных данных (например, необработанный поток данных с магнитной головки дисковода) отправляются без соответствующих часов. Приемник генерирует часы с приблизительной опорной частотой, а затем фаза выравнивает к переходам в потоке данных с ФАПЧ. Этот процесс называется восстановление тактовой частоты. Чтобы эта схема работала, поток данных должен иметь достаточно частые переходы, чтобы исправить любой дрейф в генераторе ФАПЧ. Обычно какой-то тип строкового кода, такой как 8b / 10b encoding, используется для установки жесткого верхнего предела максимального времени между переходами.

Выравнивание

Если часы отправляются параллельно с данными, эти часы можно использовать для выборки данных. Поскольку тактовые импульсы должны быть приняты и усилены, прежде чем они смогут управлять триггерами, которые осуществляют выборку данных, между обнаруженным фронтом тактового сигнала и окном полученных данных будет конечная и зависящая от процесса, температуры и напряжения задержка. Эта задержка ограничивает частоту отправки данных. Один из способов устранения этой задержки состоит в том, чтобы включить синхронизирующую схему ФАПЧ на приемной стороне, чтобы тактовая частота в каждом триггере данных согласовывалась по фазе с принятой тактовой частотой. В приложениях такого типа часто используется специальная форма ФАПЧ, называемая контуром автоподстройки частоты (DLL).

Генерация часов

Многие электронные системы включают в себя процессоры различных типов, работающих на сотнях мегагерц. Обычно тактовые импульсы, подаваемые на эти процессоры, поступают от тактовых генераторов ФАПЧ, которые умножают низкочастотные опорные тактовые импульсы (обычно 50 или 100 МГц) на рабочую частоту процессора. Коэффициент умножения может быть довольно большим в случаях, когда рабочая частота составляет несколько гигагерц, а эталонный кристалл составляет всего десятки или сотни мегагерц.

Расширенный спектр

Все электронные системы излучают некоторую нежелательную радиочастотную энергию. Различные регулирующие органы (например, FCC в США) устанавливают ограничения на излучаемую энергию и любые вызываемые ею помехи. Излучаемый шум обычно появляется на острых спектральных пиках (обычно на рабочей частоте устройства и нескольких гармониках). Разработчик системы может использовать ФАПЧ с расширенным спектром, чтобы уменьшить помехи для приемников с высокой добротностью, распределяя энергию по большей части спектра. Например, изменяя рабочую частоту вверх и вниз на небольшую величину (около 1%), устройство, работающее на сотнях мегагерц, может равномерно распределить свои помехи по спектру в несколько мегагерц, что резко снижает количество шума, наблюдаемого при вещании. FM-радио каналы с полосой пропускания в несколько десятков килогерц.

Распределение тактовых импульсов

Обычно опорные тактовые импульсы поступают в микросхему и запускают контур фазовой автоподстройки частоты (PLL ), который затем управляет распределением тактовых импульсов в системе. Распределение часов обычно сбалансировано, так что часы достигают каждой конечной точки одновременно. Одна из этих конечных точек - вход обратной связи ФАПЧ. Функция ФАПЧ состоит в том, чтобы сравнивать распределенные тактовые импульсы с входящими опорными тактовыми сигналами и изменять фазу и частоту его выхода до тех пор, пока опорные тактовые импульсы и тактовые импульсы обратной связи не будут согласованы по фазе и частоте.

ФАПЧ распространены повсеместно - они настраивают тактовые частоты в системах в несколько футов в поперечнике, а также тактовые частоты в небольших частях отдельных микросхем. Иногда эталонные часы на самом деле могут быть вовсе не чистыми часами, а скорее потоком данных с достаточным количеством переходов, чтобы ФАПЧ могла восстановить обычные часы из этого потока. Иногда опорный тактовый же частота, как часы ведомым через распределение часов, в остальное время распределенные часы могут быть некоторые рациональны кратен ссылки.

Обнаружение AM

ФАПЧ может использоваться для синхронной демодуляции сигналов с амплитудной модуляцией (AM). ФАПЧ восстанавливает фазу и частоту несущей входящего AM-сигнала. Восстановленная фаза в VCO отличается от фазы несущей на 90 °, поэтому она сдвигается по фазе для согласования, а затем подается на умножитель. Выход умножителя содержит сигналы суммарной и разностной частот, а демодулированный выходной сигнал получается с помощью фильтрации нижних частот. Поскольку ФАПЧ реагирует только на несущие частоты, которые очень близки к выходному сигналу ГУН, AM-детектор с ФАПЧ демонстрирует высокую степень селективности и помехозащищенности, что невозможно с обычными пиковыми AM-демодуляторами. Однако, цикл может потерять блокировку, где AM сигналы имеют 100% глубину модуляции.

джиттера и уменьшение шума

Одним желательным свойством всех ФАПЧ является то, что опорные и тактового сигнала обратной связи кромки быть приведены в очень близкое выравнивание. Средняя разница во времени между фазами двух сигналов, когда ФАПЧ достигла синхронизации, называется статическим фазовым сдвигом (также называемым установившейся фазовой ошибкой ). Разница между этими фазами называется отслеживанием джиттером. В идеале статический фазовый сдвиг должен быть равен нулю, а джиттер отслеживания должен быть как можно меньше.

Фазовый шум - это еще один тип джиттера, наблюдаемый в системах ФАПЧ, который вызывается самим генератором и элементами, используемыми в цепь управления частотой генератора. Известно, что одни технологии работают лучше других в этом отношении. Лучшие цифровые схемы ФАПЧ построены с элементами эмиттерной логики (ECL ) за счет высокого энергопотребления. Чтобы сохранить низкий уровень фазового шума в схемах ФАПЧ, лучше избегать насыщения логических семейств, таких как транзисторно-транзисторная логика (TTL ) или CMOS.

. Еще одним желательным свойством всех ФАПЧ является то, что фазовая и частота генерируемых часов не зависит от быстрых изменений напряжений линий питания и заземления, а также напряжения подложки, на которой изготовлены схемы ФАПЧ. Это называется подавлением шума подложки и подачи. Чем выше шумоподавление, тем лучше.

Для дальнейшего улучшения фазового шума на выходе можно использовать генератор с синхронизацией с инжекцией после ГУН в системе ФАПЧ.

Синтез частоты

В системах цифровой беспроводной связи (GSM, CDMA и т. Д.) ФАПЧ используются для обеспечения повышающего преобразования гетеродина во время передачи и понижающего преобразования во время приема. В большинстве сотовых телефонов эта функция в значительной степени интегрирована в единую интегральную схему, чтобы снизить стоимость и размер телефона. Однако из-за высокой производительности, требуемой от терминалов базовых станций, схемы передачи и приема построены из дискретных компонентов для достижения требуемых уровней производительности. Модули гетеродина GSM обычно состоят из интегральной схемы синтезатора частоты и дискретных резонаторных ГУН.

Блок-схема контура фазовой автоподстройки частоты

A фазовый детектор сравнивает два входных сигнала и выдает сигнал ошибки, пропорциональный их разности фаз. Затем сигнал ошибки фильтруется нижними частотами и используется для управления ГУН, который создает выходную фазу. Выходной сигнал подается через дополнительный делитель обратно на вход системы, создавая контур отрицательной обратной связи. Если выходная фаза дрейфует, сигнал ошибки будет увеличиваться, управляя фазой VCO в противоположном направлении, чтобы уменьшить ошибку. Таким образом, выходная фаза привязана к фазе на другом входе. Этот вход называется опорным.

Аналоговые контуры фазовой автоподстройки частоты обычно состоят из аналогового фазового детектора, фильтра нижних частот и ГУН, помещенных в конфигурацию отрицательной обратной связи. В цифровой схеме фазовой автоподстройки частоты используется цифровой фазовый детектор; он может также иметь делитель в цепи обратной связи или в опорной траектории, или обоих, для того, чтобы сделать частоту выходного сигнала системы ФАПЧ а рационально кратна опорной частоты. Не-целое число, кратное опорной частоты также может быть создано путем замены простого деления на N счетчика в цепи обратной связи с программируемым импульсного счетчиком глотанием. Этот метод обычно упоминается как синтезатор с дробным N или с ФАПЧ с дробным N.

Генератор генерирует периодический выходной сигнал. Предположим, что первоначально осциллятор находится почти одной и той же частоте, что и опорного сигнала. Если фаза от генератора отстает, что в качестве ссылки, фазовый детектор изменяет управляющее напряжение генератора таким образом, что он ускоряет. Аналогичным образом, если фаза опережает опорную, фазовый детектор изменяет управляющее напряжение, чтобы замедлить генератор. Поскольку изначально генератор может быть далек от опорной частоты, практические детекторы фазы могут также реагировать на разность частот, с тем чтобы увеличить блокировки в диапазоне допустимых входов. В зависимости от приложения либо выходной сигнал управляемого генератора, либо управляющий сигнал генератора обеспечивает полезный выход системы ФАПЧ.

фазовый детектор

Фазовый детектор (PD) генерирует напряжение, которое представляет собой разность фаз между двумя сигналами. В системе ФАПЧ два входа фазового детектора - опорный вход и обратная связь от ГУН. Выходное напряжение частичного разряда используется для управления ГУН таким образом, чтобы разность фаз между двумя входами оставалась постоянной, что делает его системой отрицательной обратной связи.

. Различные типы фазовых детекторов имеют разные рабочие характеристики.

Например, смеситель частот генерирует гармоники, которые усложняют приложения, где важна спектральная чистота сигнала VCO. Результирующие нежелательные (паразитные) боковые полосы, также называемые «», могут доминировать над требованиями фильтра и значительно уменьшать диапазон захвата или увеличивать время захвата сверх требований. В этих приложениях используются более сложные цифровые фазовые детекторы, которые не имеют на выходе столь серьезного эталонного паразитного компонента. Кроме того, в синхронизированном состоянии установившаяся разность фаз на входах, использующих этот тип фазового детектора, составляет около 90 градусов.

В приложениях с ФАПЧ часто требуется знать, когда контур находится вне синхронизации. Более сложные цифровые фазочастотные детекторы обычно имеют выход, позволяющий надежно указать состояние отсутствия синхронизации.

Логический элемент XOR часто используется для цифровых ФАПЧ в качестве эффективного, но простого фазового детектора. Его также можно использовать в аналоговом смысле с небольшими изменениями схемы.

Фильтр

Блок, обычно называемый контурным фильтром ФАПЧ (обычно фильтром нижних частот), обычно имеет две различные функции.

Основная функция - определение динамики контура, также называемой стабильностью. Это, как петля реагирует на нарушения, такие, как изменения в опорной частоте, изменения делителя обратной связи, либо при запуске. Общие соображения - это диапазон, в котором контур может достичь блокировки (диапазон втягивания, диапазон захвата или диапазон захвата), насколько быстро цикл достигает фиксации (время захвата, время блокировки или время установления ) и демпфирование поведение. В зависимости от приложения для этого может потребоваться одно или несколько из следующего: простая пропорция (усиление или затухание), интеграл (фильтр нижних частот) и / или производная (фильтр высоких частот ). Для этого обычно исследуются параметры контура: запас усиления контура и запас по фазе. Общие концепции в теории управления, включая ПИД-регулятор, используются для разработки этой функции.

Второе общее соображение ограничивает количество энергии опорной частоты (пульсация), появляющееся на выходе фазового детектора, который затем применяется к управляющему входу ГУН. Эта частота модулирует VCO и создает боковые полосы FM, обычно называемые «эталонными парами».

В конструкции этого блока может преобладать любое из этих соображений, или он может быть сложным процессом, сочетающим взаимодействие двух. Типичный компромисс: увеличение полосы пропускания обычно ухудшает стабильность или слишком большое демпфирование для лучшей стабильности снижает скорость и увеличивает время установления. Часто также сказывается фазовый шум.

Генератор

Во всех контурах фазовой автоподстройки частоты используется элемент генератора с возможностью регулирования частоты. Это может быть аналоговый ГУН, управляемый аналоговой схемой в случае APLL или управляемый цифровым способом с использованием цифро-аналогового преобразователя , как в случае некоторых схем DPLL. В ADPLL используются чистые цифровые генераторы, такие как генератор с числовым управлением.

Путь обратной связи и дополнительный делитель

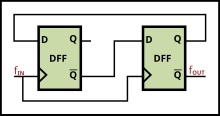Пример цифрового делителя (на 4) для использования в тракте обратной связи умножающей системы ФАПЧ

PLL может включать в себя делитель между генератором и входом обратной связи к фазовому детектору для создания синтезатора частоты. Программируемый делитель особенно полезен в радиопередатчиках, поскольку большое количество частот передачи может быть создано одним стабильным, точным, но дорогим опорным генератором, управляемым кварцевым кристаллом..

Некоторые системы ФАПЧ также включают делитель между опорный тактовый и опорный вход фазового детектора. Если делитель в тракте обратной связи делится на $N\; \{\backslash \; displaystyle\; N\}$, а делитель входного эталонного сигнала делится на $M\; \{\backslash \; displaystyle\; M\}$, это позволяет ФАПЧ для умножения опорной частоты с помощью $N\; /\; M\; \{\backslash \; displaystyle\; N\; /\; M\}$. Может показаться, что проще просто подать на ФАПЧ более низкую частоту, но в некоторых случаях опорная частота может быть ограничена другими проблемами, и тогда может быть полезен опорный делитель.

умножение частоты также может быть достигнуто путем блокировки выходного сигнала ГУН-й гармоники опорного сигнала. Вместо простого фазового детектора в конструкции используется смеситель гармоник (смеситель выборки). Смеситель на гармониках превращает опорный сигнал в последовательность импульсов, богатую гармониками. Выход ГУН настроен грубо, чтобы быть близким к одной из этих гармоник. Следовательно, желаемый выходной сигнал смесителя гармоник (представляющий разницу между N-гармоникой и выходом ГУН) попадает в полосу пропускания контурного фильтра.

Следует также отметить, что обратная связь не ограничивается делителем частоты. Этим элементом могут быть другие элементы, такие как умножитель частоты или смеситель. Умножитель будет сделать вывод ГУН суб-кратно (а не кратное) опорной частоты. Смеситель может преобразовывать частоту ГУН на фиксированное смещение. Это также может быть их комбинация. Пример - разделитель, следующий за смесителем; это позволяет делителю работать на гораздо более низкой частоте, чем ГУН, без потери в усилении контура.

Модель APLL во временной области

Уравнения, управляющие контуром фазовой автоподстройки частоты с аналоговым умножителем в качестве фазового детектора и линейного фильтра, могут быть получены следующим образом. Пусть на входе фазового детектора будет $f\; 1\; (\theta \; 1\; (t))\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\backslash \; theta\; \_\; \{1\}\; (t))\}$, а на выходе ГУН равен $f\; 2\; (\theta \; 2\; (t))\; \{\backslash \; displaystyle\; f\_\; \{2\}\; (\backslash \; theta\; \_\; \{2\}\; (t))\}$с фазами $\theta \; 1\; (t)\; \{\; \backslash \; Displaystyle\; \backslash \; theta\; \_\; \{1\}\; (t)\}$и $\theta \; 2\; (t)\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{2\}\; (t)\}$. Функции $f\; 1\; (\theta )\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\backslash \; theta)\}$и $f\; 2\; (\theta )\; \{\backslash \; displaystyle\; f\_\; \{2\}\; (\backslash \; theta)\}$описывают формы сигналов. Тогда выходной сигнал фазового детектора $\phi \; (t)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (t)\}$определяется как

$\phi \; (t)\; =\; f\; 1\; (\theta \; 1\; (t))\; f\; 2\; (\theta \; 2\; (t))\; \{\backslash \; displaystyle\; \backslash \; varphi\; (t)\; =\; f\_\; \{1\}\; (\backslash \; theta\; \_\; \{1\}\; (t))\; f\_\; \{2\}\; (\backslash \; theta\; \_\; \{2\}\; (t))\}$

Частота ГУН обычно берется как функция входного ГУН $g\; (t)\; \{\backslash \; displaystyle\; g\; (t)\}$как

$\theta \; \dot{}\; 2\; (t)\; =\; \omega \; 2\; (t)\; =\; \omega \; бесплатно\; +\; gvg\; (t)\; \{\backslash \; displaystyle\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \_\; \{2\}\; (t)\; =\; \backslash \; omega\; \_\; \{2\}\; (t)\; =\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\; +\; g\_\; \{v\}\; g\; (t)\; \backslash ,\}$

где $gv\; \{\backslash \; displaystyle\; g\_\; \{v\}\}$- чувствительность ГУН, выраженная в Гц / В; $\omega \; free\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\}$- частота автономного режима VCO.

Петлевой фильтр можно описать системой линейных дифференциальных уравнений

$x\; \dot{}\; =\; A\; x\; +\; b\; \phi \; (t),\; g\; (t)\; =\; c\; \ast \; x,\; x\; (0)\; =\; x\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rcl\}\; \{\backslash \; dot\; \{x\}\}\; =\; Ax\; +\; b\; \backslash \; varphi\; (t),\; \backslash \backslash \; g\; (t)\; =\; c\; ^\; \{*\}\; x,\; \backslash \; end\; \{array\; \}\}\; \backslash \; quad\; x\; (0)\; =\; x\_\; \{0\},\}$

где $\phi \; (t)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (t)\}$- вход фильтра, $g\; (t)\; \{\backslash \; displaystyle\; g\; (t)\}$- результат фильтра, $A\; \{\backslash \; displaystyle\; A\}$- $n\; \{\backslash \; displaystyle\; n\; \}$по- $n\; \{\backslash \; displaystyle\; n\}$матрица, $x\; \in \; C\; n,\; b\; \in \; R\; n,\; c\; \in \; C\; n,\; \{\backslash \; displaystyle\; x\; \backslash \; в\; \backslash \; mathbb\; \{C\}\; ^\; \{n\},\; \backslash \; quad\; b\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{n\},\; \backslash \; quad\; c\; \backslash \; in\; \backslash \; mathbb\; \{C\}\; ^\; \{n\},\; \backslash \; quad\}$. $x\; 0\; \in \; C\; n\; \{\backslash \; displaystyle\; x\_\; \{0\}\; \backslash \; in\; \backslash \; mathbb\; \{C\}\; ^\; \{n\}\}$представляет начальное состояние фильтра. Звездочка - это сопряженное транспонирование.

Следовательно, следующая система описывает ФАПЧ

$x\; \dot{}\; =\; A\; x\; +\; bf\; 1\; (\theta \; 1\; (t))\; f\; 2\; (\theta \; 2\; (t)),\; \theta \; \dot{}\; 2\; =\; \omega \; бесплатно\; +\; gv\; (c\; \ast \; x)\; x\; (0)\; =\; x\; 0,\; \theta \; 2\; (0)\; =\; \theta \; 0.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rcl\}\; \{\backslash \; dot\; \{x\}\}\; =\; Ax\; +\; bf\_\; \{1\}\; (\backslash \; theta\; \_\; \{1\}\; (t))\; f\_\; \{2\}\; (\backslash \; theta\; \_\; \{2\}\; (\; t)),\; \backslash \backslash \; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \_\; \{2\}\; =\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\; +\; g\_\; \{v\}\; (c\; ^\; \{*\}\; x)\; \backslash \backslash \backslash \; end\; \{array\; \}\}\; \backslash \; quad\; x\; (0)\; =\; x\_\; \{0\},\; \backslash \; quad\; \backslash \; theta\; \_\; \{2\}\; (0)\; =\; \backslash \; theta\; \_\; \{0\}.\}$

где $\theta \; 0\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\; 0\}\}$- начальный фазовый сдвиг.

Модель APLL в фазовой области

Рассмотрим вход PLL $f\; 1\; (\theta \; 1\; (t))\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\backslash \; theta\; \_\; \{1\}\; (t))\}$и выход ГУН $f\; 2\; (\theta \; 2\; (t))\; \{\backslash \; displaystyle\; f\_\; \{2\}\; (\backslash \; theta\; \_\; \{2\}\; (t))\}$высокочастотные сигналы. Тогда для любой кусочно дифференцируемой $2\; \pi \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\}$-периодической функции $f\; 1\; (\theta )\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\backslash \; theta)\}$и $f\; 2\; (\theta )\; \{\backslash \; displaystyle\; f\_\; \{2\}\; (\backslash \; theta)\}$есть функция $\phi \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; varphi\; (\backslash \; theta)\}$так, что на выходе $G\; (t)\; \{\backslash \; displaystyle\; G\; (t)\}$фильтра

$x\; \dot{}\; =\; A\; x\; +\; b\; \phi \; (\theta \; 1\; (t)\; -\; \theta \; 2\; (t)),\; G\; (t)\; =\; c\; \ast \; x,\; x\; (0)\; =\; x\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rcl\}\; \{\backslash \; dot\; \{x\}\}\; =\; Ax\; +\; b\; \backslash \; varphi\; (\backslash \; theta\; \_\; \{1\}\; (t)\; -\; \backslash \; theta\; \_\; \{2\}\; (t)),\; \backslash \backslash \; G\; (t)\; =\; c\; ^\; \{*\}\; x,\; \backslash \; end\; \{array\}\}\; \backslash \; quad\; x\; (0)\; =\; x\_\; \{0\},\}$

в фазовой области асимптотически равно (разность $G\; (t)\; -\; g\; (t)\; \{\backslash \; displaystyle\; G\; (t)\; -g\; (t)\}$мала по отношению к частотам) на выходе модели фильтра во временной области. Здесь функция $\phi \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; varphi\; (\backslash \; theta)\}$- это характеристика фазового детектора.

, обозначенная $\theta \; \Delta \; (t)\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; Delta\}\; (t)\}$разность фаз

$\theta \; \Delta \; =\; \theta \; 1\; (t)\; -\; \theta \; 2\; (t).\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; Delta\}\; =\; \backslash \; theta\; \_\; \{1\}\; (t)\; -\; \backslash \; theta\; \_\; \{2\}\; (t).\}$

Тогда следующая динамическая система описывает поведение PLL

$x\; \dot{}\; =\; A\; x\; +\; b\; \phi \; (\theta \; \Delta ),\; \theta \; \dot{}\; \Delta \; =\; \omega \; \Delta \; -\; gv\; (c\; \ast \; x).\; х\; (0)\; =\; х\; 0,\; \theta \; \Delta \; (0)\; =\; \theta \; 1\; (0)\; -\; \theta \; 2\; (0).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rcl\}\; \{\backslash \; dot\; \{x\}\}\; =\; Ax\; +\; b\; \backslash \; varphi\; (\backslash \; theta\; \_\; \{\backslash \; Delta\}),\; \backslash \backslash \; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \_\; \{\backslash \; Delta\; \}\; =\; \backslash \; omega\; \_\; \{\backslash \; Delta\}\; -g\_\; \{v\}\; (c\; ^\; \{*\}\; x).\; \backslash \backslash \backslash \; end\; \{array\}\}\; \backslash \; quad\; x\; (0)\; =\; x\_\; \{0\},\; \backslash \; quad\; \backslash \; theta\; \_\; \{\backslash \; Delta\}\; (0)\; =\; \backslash \; theta\; \_\; \{1\}\; (0)\; -\; \backslash \; theta\; \_\; \{2\}\; (0).\}$

Здесь $\omega \; \Delta \; =\; \omega \; 1\; -\; \omega \; бесплатно\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{\backslash \; Delta\}\; =\; \backslash \; omega\; \_\; \{1\}\; -\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\}$; $\omega \; 1\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{1\}\}$- частота ссылки осциллятор (мы предполагаем, что $\omega \; free\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\}$является постоянным).

Пример

Рассмотрим синусоидальные сигналы

$f\; 1\; (\theta \; 1\; (t))\; =\; A\; 1\; sin\; \; (\theta \; 1\; (t)),\; f\; 2\; (\theta \; 2\; (t))\; Знак\; равно\; A\; 2\; соз\; \; (\theta \; 2\; (t))\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\backslash \; theta\; \_\; \{1\}\; (t))\; =\; A\_\; \{1\}\; \backslash \; sin\; (\backslash \; theta\; \_\; \{1\}\; (t)),\; \backslash \; quad\; f\_\; \{2\}\; (\backslash \; theta\; \_\; \{2\}\; (t))\; =\; A\_\; \{2\}\; \backslash \; cos\; (\backslash \; theta\; \_\; \{2\}\; (t))\}$

и простая однополюсная RC-цепь как фильтр. Модель во временной области принимает вид

$x\; \dot{}\; =\; -\; 1\; RC\; x\; +\; 1\; RCA\; 1\; A\; 2\; sin\; \; (\theta \; 1\; (t))\; cos\; \; (\theta \; 2\; (t)),\; \theta \; \dot{}\; 2\; =\; \omega \; free\; +\; gv\; (c\; *\; x)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; dot\; \{x\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{RC\}\}\; x\; +\; \{\backslash \; frac\; \{1\}\; \{RC\}\}\; A\_\; \{1\}\; A\_\; \{2\}\; \backslash \; sin\; (\backslash \; theta\; \_\; \{1\}\; (t))\; \backslash \; cos\; (\backslash \; theta\; \_\; \{2\}\; (t)),\; \backslash \backslash \; [6pt]\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \_\; \{2\}\; =\; \backslash \; omega\; \_\; \{\backslash \; text\; \{free\}\}\; +\; g\_\; \{v\}\; (c\; ^\; \{*\}\; x)\; \backslash \; end\; \{align\}\}\}$

Характеристики частичных разрядов для этих сигналов равны

$\phi \; (\theta \; 1\; -\; \theta \; 2)\; знак\; равно\; A\; 1\; A\; 2\; 2\; грех\; \; (\theta \; 1\; -\; \theta \; 2)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (\backslash \; theta\; \_\; \{1\}\; -\; \backslash \; theta\; \_\; \{2\})\; =\; \{\backslash \; frac\; \{A\_\; \{1\}\; A\_\; \{2\}\; \}\; \{2\}\}\; \backslash \; sin\; (\backslash \; theta\; \_\; \{1\}\; -\; \backslash \; theta\; \_\; \{2\})\}$

Следовательно, модель фазовой области принимает вид

$x\; \dot{}\; =\; -\; 1\; RC\; x\; +\; 1\; RCA\; 1\; A\; 2\; 2\; sin\; \; (\theta \; \Delta ),\; \theta \; \dot{}\; \Delta \; =\; \omega \; \Delta \; -\; gv\; (c\; \ast \; x).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; dot\; \{x\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{RC\}\}\; x\; +\; \{\backslash \; frac\; \{1\}\; \{RC\}\}\; \{\backslash \; frac\; \{A\_\; \{1\}\; A\_\; \{\; 2\}\}\; \{2\}\}\; \backslash \; sin\; (\backslash \; theta\; \_\; \{\backslash \; Delta\}),\; \backslash \backslash \; [6pt]\; \{\backslash \; dot\; \{\backslash \; theta\}\}\; \_\; \{\backslash \; Delta\}\; =\; \backslash \; omega\; \_\; \{\backslash \; Delta\}\; -g\_\; \{v\; \}\; (c\; ^\; \{*\}\; x).\; \backslash \; end\; \{align\}\}\}$

Эта система уравнений эквивалентна уравнению математического маятника

$x = θ ˙ 2 - ω 2 gvc ∗ = ω 1 - θ ˙ Δ - ω 2 gvc ∗, x ˙ = θ ¨ 2 gvc ∗, θ 1 = ω 1 t + Ψ, θ Δ = θ 1 - θ 2, θ ˙ Δ = θ ˙ 1 - θ ˙ 2 = ω 1 - θ ˙ 2, 1 gvc ∗ θ ¨ Δ - 1 gvc ∗ RC θ ˙ Δ - A 1 A 2 2 RC sin ⁡ θ Δ = ω 2 - ω 1 gvc ∗ RC. {\ displaystyle {\ begin {align} x = {\ frac {{\ dot {\ theta}} _ {2} - \ omega _ {2}} {g_ {v} c ^ {*}}} = {\ frac {\ omega _ {1} - {\ dot {\ theta}} _ {\ Delta} - \ omega _ {2}} {g_ {v} c ^ {*}}}, \\ [6pt] {\ точка {x}} = {\ frac {{\ ddot {\ theta}} _ {2}} {g_ {v} c ^ {*}}}, \\ [6pt] \ theta _ {1} = \ omega _ {1} t + \ Psi, \\ [6pt] \ theta _ {\ Delta} = \ theta _ {1} - \ theta _ {2}, \\ [6pt] {\ dot {\ theta} } _ {\ Delta} = {\ dot {\ theta}} _ {1} - {\ dot {\ theta}} _ {2} = \ omega _ {1} - {\ dot {\ theta}} _ {2}, \\ [6pt] и {\ frac {1} {g_ {v} c ^ {*}}} {\ ddot {\ theta}} _ {\ Delta} - {\ frac {1} {g_ {v} c ^ {*} RC}} {\ dot {\ theta}} _ {\ Delta} - {\ frac {A_ {1} A_ {2 }} {2RC}} \ sin \ theta _ {\ Delta} = {\ frac {\ omega _ {2} - \ omega _ {1}} {g_ {v} c ^ {*} RC}}. \ End {align}}}$

Модель линеаризованной фазовой области

Цепи фазовой автоподстройки частоты также могут быть проанализированы как системы управления путем применения преобразования Лапласа. Ответ цикла может быть записан как

$\theta \; о\; \theta \; я\; =\; К\; п\; К\; v\; F\; (s)\; s\; +\; K\; p\; K\; v\; F\; (s)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; theta\; \_\; \{o\}\}\; \{\backslash \; theta\; \_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\}\; F\; (s)\}\; \{s\; +\; K\_\; \{p\}\; K\_\; \{v\}\; F\; (s)\}\}\}$

Где

• $\theta \; o\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{o\}\}$- фаза вывода в радианах
• $\theta \; i\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{i\}\}$- вход фаза в радианах
• $K\; p\; \{\backslash \; displaystyle\; K\_\; \{p\}\}$- коэффициент усиления фазового детектора в вольт на радиан
• $K\; v\; \{\backslash \; displaystyle\; K\_\; \{v\}\}$- коэффициент усиления ГУН в радианах на вольт- секунда
• $F\; (s)\; \{\backslash \; displaystyle\; F\; (s)\}$- передаточная функция контурного фильтра (безразмерная)

Характеристики контура можно регулировать, вставляя различные типы контурных фильтров. Самый простой фильтр - однополюсная RC-цепь. Передаточная функция цикла в этом случае равна

$F\; (s)\; =\; 1\; 1\; +\; s\; RC\; \{\backslash \; displaystyle\; F\; (s)\; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; sRC\}\}\}$

Ответ цикла выглядит следующим образом:

$\theta \; о\; \theta \; я\; знак\; равно\; К\; п\; К\; v\; RC\; s\; 2\; +\; s\; RC\; +\; К\; п\; К\; v\; RC\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; theta\; \_\; \{o\}\}\; \{\backslash \; theta\; \_\; \{i\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\}\}\; \{RC\}\}\; \{s\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{s\}\; \{RC\}\}\; +\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\}\}\; \{\; RC\}\}\}\}\}$

Это разновидность классического гармонического осциллятора. Знаменатель может быть связан со знаменателем системы второго порядка:

$s\; 2\; +\; 2\; s\; \zeta \; \omega \; n\; +\; \omega \; n\; 2\; \{\backslash \; displaystyle\; s\; ^\; \{2\}\; +\; 2s\; \backslash \; zeta\; \backslash \; omega\; \_\; \{n\}\; +\; \backslash \; omega\; \_\; \{n\}\; ^\; \{2\}\}$

, где $\zeta \; \{\backslash \; displaystyle\; \backslash \; zeta\}$- коэффициент демпфирования, а $\omega \; n\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{n\}\}$- собственная частота контура.

Для однополюсного RC-фильтра

$\omega \; n\; =\; K\; p\; K\; v\; RC\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{n\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\})\; \}\; \{RC\}\}\}\}$

$\zeta \; =\; 1\; 2\; К\; п\; К\; v\; RC\; \{\backslash \; displaystyle\; \backslash \; zeta\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{K\_\; \{p\}\; K\_\; \{v\}\; RC\}\}\}\}\; \}$

Собственная частота контура является мерой времени отклика контура, а коэффициент демпфирования - мерой выброса и звона. В идеале собственная частота должна быть высокой, а коэффициент демпфирования должен быть около 0,707 (критическое демпфирование). С однополюсным фильтром невозможно независимо регулировать частоту контура и коэффициент демпфирования. Для случая критического демпфирования

$RC\; =\; 1\; 2\; K\; p\; K\; v\; \{\backslash \; displaystyle\; RC\; =\; \{\backslash \; frac\; \{1\}\; \{2K\_\; \{p\}\; K\_\; \{v\}\}\}\}$

$\omega \; c\; =\; K\; p\; K\; v\; 2\; \{\backslash \; displaystyle\; \backslash \; omega\; \_\; \{c\}\; =\; K\_\; \{p\}\; K\_\; \{v\}\; \{\backslash \; sqrt\; \{2\}\}\}$

Чуть более эффективный фильтр, фильтр с опережением задержки включает один полюс и один ноль. Это может быть реализовано с помощью двух резисторов и одного конденсатора. Передаточная функция для этого фильтра:

$F\; (s)\; =\; 1\; +\; s\; CR\; 2\; 1\; +\; s\; C\; (R\; 1\; +\; R\; 2)\; \{\backslash \; displaystyle\; F\; (s)\; =\; \{\backslash \; frac\; \{1\; +\; sCR\_\; \{2\}\}\; \{1\; +\; sC\; (R\_\; \{1\}\; +\; R\_\; \{2\})\}\}\}$

Этот фильтр имеет две постоянные времени

$\tau \; 1\; =\; C\; (R\; 1\; +\; R\; 2)\; \{\backslash \; displaystyle\; \backslash \; tau\; \_\; \{1\}\; =\; C\; (R\_\; \{1\}\; +\; R\_\; \{2\})\}$

$\tau \; 2\; =\; CR\; 2\; \{\backslash \; displaystyle\; \backslash \; tau\; \_\; \{2\}\; =\; CR\_\; \{2\}\}$

Подстановка выше дает следующие собственные частота и коэффициент демпфирования

$\omega \; N\; =\; К\; п\; К\; v\; \tau \; 1\; \{\backslash \; Displaystyle\; \backslash \; omega\; \_\; \{n\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\}\}\; \{\backslash \; tau\; \_\; \{1\}\}\}\}\}$

$\zeta \; знак\; равно\; 1\; 2\; \omega \; N\; \tau \; 1\; +\; \omega \; N\; \tau \; 2\; 2\; \{\backslash \; displaystyle\; \backslash \; zeta\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; omega\; \_\; \{n\}\; \backslash \; tau\; \_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{\backslash \; omega\; \_\; \{n\}\; \backslash \; tau\; \_\; \{2\}\}\; \{2\}\}\}$

Компоненты контурного фильтра могут быть рассчитаны независимо для заданной собственной частоты и коэффициента демпфирования

$\tau \; 1\; =\; K\; p\; K\; v\; \omega \; n\; 2\; \{\; \backslash \; Displaystyle\; \backslash \; tau\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{K\_\; \{p\}\; K\_\; \{v\}\}\; \{\backslash \; omega\; \_\; \{n\}\; ^\; \{2\}\}\}\}$

$\tau \; 2\; =\; 2\; \zeta \; \omega \; n\; -\; 1\; K\; p\; К\; v\; \{\backslash \; displaystyle\; \backslash \; tau\; \_\; \{2\}\; =\; \{\backslash \; frac\; \{2\; \backslash \; zeta\}\; \{\backslash \; omega\; \_\; \{n\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{K\_\; \{p\}\; K\_\; \{v\}\}\}\}$

Конструкция контурного фильтра в реальном мире может быть намного сложнее, например использование фильтров более высокого порядка для уменьшения различных типов или источников фазового шума. (См. Ссылку Д. Банерджи ниже)

Программная реализация цифровой схемы фазовой автоподстройки частоты

Цифровые схемы фазовой автоподстройки частоты могут быть реализованы аппаратно с использованием интегральных схем, таких как CMOS 4046. Однако, Поскольку микроконтроллеры становятся все быстрее, может иметь смысл реализовать контур фазовой автоподстройки частоты в программном обеспечении для приложений, которые не требуют блокировки сигналов в диапазоне МГц или выше, например, для точного управления скоростью двигателя. Программная реализация имеет несколько преимуществ, включая простую настройку контура обратной связи, включая изменение коэффициента умножения или деления между отслеживаемым сигналом и выходным генератором. Кроме того, полезно разбираться в программной реализации и экспериментировать с ней. В качестве примера петли фазовой автоподстройки частоты, реализованной с использованием фазово-частотного детектора, представлен в MATLAB, поскольку этот тип фазового детектора является надежным и простым в реализации.

% Этот пример написан в MATLAB% Initialize variables vcofreq = zeros (1, numiterations); ervec = нули (1, цифры); % Отслеживать последние состояния задания, сигнала и сигнала ошибки qsig = 0; qref = 0; lref = 0; lsig = 0; lersig = 0; phs = 0; freq = 0; % Константы петлевого фильтра (пропорциональные и производные)% В настоящее время степени двойки для облегчения умножения на сдвиги prop = 1/128; производная = 64; для it = 1: numiterations% Имитируйте гетеродин с помощью 16-битного счетчика phs = mod (phs + floor (freq / 2 ^ 16), 2 ^ 16); ref = phs < 32768; % Get the next digital value (0 or 1) of the signal to track sig = tracksig(it); % Implement the phase-frequency detector rst = ~ (qsig qref); % Reset the "flip-flop" of the phase-frequency % detector when both signal and reference are high qsig = (qsig | (sig ~ lsig)) rst; % Trigger signal flip-flop and leading edge of signal qref = (qref | (ref ~ lref)) rst; % Trigger reference flip-flop on leading edge of reference lref = ref; lsig = sig; % Store these values for next iteration (for edge detection) ersig = qref - qsig; % Compute the error signal (whether frequency should increase or decrease) % Error signal is given by one or the other flip flop signal % Implement a pole-zero filter by proportional and derivative input to frequency filtered_ersig = ersig + (ersig - lersig) * deriv; % Keep error signal for proportional output lersig = ersig; % Integrate VCO frequency using the error signal freq = freq - 2 ^ 16 * filtered_ersig * prop; % Frequency is tracked as a fixed-point binary fraction % Store the current VCO frequency vcofreq(1, it) = freq / 2 ^ 16; % Store the error signal to show whether signal or reference is higher frequency ervec(1, it) = ersig; end

В этом примере предполагается, что массив trackigсодержит опорный сигнал, который необходимо отслеживать. Генератор реализован в виде счетчика, причем старший бит счетчика указывает состояние включения / выключения генератора. Этот код имитирует два D-типа триггера, которые составляют компаратор фаза-частота. Когда либо задание, либо сигнал имеют положительный фронт, соответствующий триггер переключается на высокий уровень. Когда и задание, и сигнал становятся высокими, оба триггера сбрасываются. Какой триггер высокий, определяет в этот момент, опережает ли опорный сигнал или сигнал. Сигналом ошибки является разница между этими двумя значениями триггера. Фильтр полюс-ноль реализуется путем добавления сигнала ошибки и его производной к отфильтрованному сигналу ошибки. Это, в свою очередь, интегрируется, чтобы найти частоту генератора.

На практике, вероятно, можно было бы добавить другие операции в обратную связь этого контура фазовой автоподстройки частоты. Например, если бы в контуре фазовой автоподстройки частоты был реализован умножитель частоты, сигнал генератора можно было бы разделить по частоте, прежде чем сравнивать его с опорным сигналом.

• Контур ФАПЧ
• Контур ФАПЧ-накачки
• Восстановление несущей
• Круговая карта - простая математическая модель контура ФАПЧ, показывающая как с синхронизацией мод, так и с хаотическим поведением.
• Петля Костаса
• Петля с задержкой (DLL)
• Приемник прямого преобразования
• Прямой цифровой синтезатор
• Фильтр Калмана
• Многобитная ФАПЧ
• Shortt – Synchronome clock - Ведомый маятник с синхронизацией по фазе с ведущим (около 1921 г.)

Викискладе есть носители, относящиеся к Петли с фазовой синхронизацией.

• Банерджи, Дин (2006), PLL Performance, Simulation and Design Handbook (4 ed.), National Semiconductor, заархивировано с исходный от 02.09.2012, извлечен 04.12.2012.
• Best, RE (2003), Phase-locked Loops: Design, Simulation and Applications, McGraw-Hill, ISBN 0-07-141201-8
• де Беллескиз, Анри (июнь 1932 г.), "La réception Synchrone", L'Onde Electrique, 11 : 230–240
• Дорф, Ричард К. (1993), Справочник по электротехнике, Бока-Ратон: CRC Press, Bibcode : 1993eeh..book..... D, ISBN 0-8493-0185-8
• Иган, Уильям Ф. (1998), Основы фазовой синхронизации, John Wiley Sons. (предоставляет полезные сценарии Matlab для моделирования)
• Иган, Уильям Ф. (2000), Синтез частот с помощью фазовой синхронизации (2-е изд.), Джон Уайли и сыновья. (предоставляет полезные сценарии Matlab для моделирования)
• Gardner, Floyd M. (2005), Phaselock Techniques (3-е изд.), Wiley-Interscience, ISBN 978-0-471 -43063-6
• Klapper, J.; Франкл, Дж. Т. (1972), Системы с фазовой синхронизацией и частотной обратной связью, Academic Press. (FM демодуляция)
• Кундерт, Кен (август 2006 г.), Прогнозирование фазового шума и джиттера синтезаторов частоты на основе ФАПЧ (PDF) (редакция 4g), Designer's Guide Consulting, Inc.
• Лю, Минлян (21 февраля 2006 г.), Build a 1.5-V 2.4 GHz CMOS PLL, Wireless Net Design Line, заархивировано из оригинала 1 июля 2010 г.. Статья о разработке стандартной ИС ФАПЧ для приложений Bluetooth.
• Волавер, Дэн Х. (1991), Phase-Lock Loop Circuit Design, Prentice Hall, ISBN 0-13-662743- 9

• Праймер для фазовой автоподстройки частоты - включает встроенное видео