Петля Костаса

редактировать

Схема демодулятора на основе петли Фазовой автоподстройки частоты

A Петля Костаса представляет собой контур фазовой автоподстройки частоты Схема на основе (PLL), которая используется для несущей частоты восстановления из сигналов с подавленной несущей модуляции (например, сигналов двойной боковой полосы подавленной несущей) и сигналы фазовой модуляции (например, BPSK, QPSK ). Он был изобретен Джоном П. Костасом в General Electric в 1950-х годах. Его изобретение было описано как оказавшее «глубокое влияние на современные цифровые коммуникации». Основное применение петель Костаса - беспроводные приемники. Его преимущество перед другими детекторами на основе ФАПЧ состоит в том, что при небольших отклонениях напряжение ошибки контура Костаса составляет $sin ⁡ (2 (θ i - θ f)) {\ displaystyle \ sin (2 (\ theta _ {i} - \ theta _ {f}))}$ $\ sin (2 (\ theta_i- \ theta_f))$ по сравнению с $sin ⁡ (θ i - θ f) {\ displaystyle \ sin (\ theta _ {i} - \ theta _ {f})}$ $\ sin (\ theta_i- \ theta_f)$ . Это увеличивает вдвое чувствительность, а также делает петлю Костаса уникально подходящей для отслеживания несущих с доплеровским смещением, особенно в OFDM и GPS-приемниках.

Содержание

1 Классический реализация
2 Математические модели
- 2.1 Во временной области
- 2.2 В фазово-частотной области
3 Получение частоты
4 Петля QPSK Костаса
5 Ссылки

Классическая реализация

Петля Костаса, работающая в заблокированном состоянии.

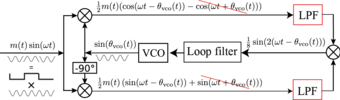
В классической реализации петли Костаса, локальный генератор, управляемый напряжением (ГУН), обеспечивает квадратурные выходы, по одному на каждый из двух фазовые детекторы, например, детекторы продукта. Одна и та же фаза входного сигнала также применяется к обоим фазовым детекторам, а выходной сигнал каждого фазового детектора проходит через фильтр нижних частот. Выходы этих фильтров нижних частот являются входами другого фазового детектора, выход которого проходит через шумоподавляющий фильтр, прежде чем использоваться для управления генератором, управляемым напряжением. Общий отклик контура контролируется двумя отдельными фильтрами нижних частот, которые предшествуют третьему фазовому детектору, в то время как третий фильтр нижних частот играет тривиальную роль с точки зрения усиления и запаса по фазе.

Приведенный выше рисунок петли Костаса нарисован в состоянии "заблокированного" состояния, когда частота ГУН и входящая несущая частота стали одинаковыми в результате процесса петли Костаса. Цифра не соответствует «разблокированному» состоянию.

Математические модели

Во временной области

Модель во временной области цикла BPSK Костаса

В простейшем случае $m 2 (t) = 1 {\ displaystyle m ^ {2} (t) = 1}$ $m ^ {2} (t) = 1$ . Следовательно, $m 2 (t) = 1 {\ displaystyle m ^ {2} (t) = 1}$ $m ^ {2} (t) = 1$ не влияет на вход фильтра шумоподавления. Сигналы несущей и генератора, управляемого напряжением (VCO), представляют собой периодические колебания $fref, vco (θ ref, vco (t)) {\ displaystyle f_ {ref, vco} (\ theta _ {ref, vco} (t))}$ ${\ displaystyle f_ {ref, vco} (\ theta _ {ref, vco} (t))}$ с высокими частотами $θ ˙ ref, vco (t) {\ displaystyle {\ dot {\ theta}} _ {ref, vco} (t)}$ ${ \ displaystyle {\ dot {\ theta}} _ {ref, vco} (t)}$ . Блок $⨂ {\ displaystyle \ bigotimes}$ $\ bigotimes$ является аналоговым умножителем.

С математической точки зрения линейный фильтр может быть описан системой линейные дифференциальные уравнения

x ˙ = A x + bud (t), u LF = c ∗ x. {\ displaystyle {\ begin {array} {ll} {\ dot {x}} = Ax + bu_ {d} (t), u_ {LF} = c ^ {*} x. \ end {array}}}

{\ displaystyle {\ begin {array} {ll} { \ dot {x}} = Ax + bu_ {d} (t), u_ {LF} = c ^ {*} x. \ end {array}}}

Здесь $A {\ displaystyle A}$ $A$ - постоянная матрица, $x (t) {\ displaystyle x (t)}$ $x(t)$ - вектор состояния filter, $b {\ displaystyle b}$ $b$ и $c {\ displaystyle c}$ $c$ - постоянные векторы.

Модель ГУН обычно считается линейной

θ ˙ vco (t) = ω vcofree + K vcou LF (t), t ∈ [0, T], {\ displaystyle {\ begin {array} {ll} {\ dot {\ theta}} _ {vco} (t) = \ omega _ {vco} ^ {free} + K_ {vco} u_ {LF} (t), t \ in [ 0, T], \ end {array}}}

{\ displaystyle {\ begin {array} {ll} {\ dot {\ theta}} _ {vco} (t) = \ omega _ {vco} ^ {free} + K_ {vco} u_ {LF} (t), t \ в [0, T], \ end {array}}}

где $ω vcofree {\ displaystyle \ omega _ {vco} ^ {free}}$ ${\ displaystyle \ omega _ {vco} ^ {free}}$ - это частота свободного хода напряжения управляемый генератор, а $K vco {\ displaystyle K_ {vco}}$ ${\ displa ystyle K_ {vco}}$ - коэффициент усиления генератора. Аналогичным образом можно рассматривать различные нелинейные модели ГУН.

Предположим, что частота задающего генератора постоянна. $θ ˙ r e f (t) ≡ ω r e f. {\ displaystyle {\ dot {\ theta}} _ {ref} (t) \ Equiv \ omega _ {ref}.}$ ${\ displaystyle {\ dot {\ theta}} _ {ref} (t) \ Equiv \ omega _ {ref}.}$ Уравнение ГУН и уравнение выхода фильтра

x ˙ = A x + bfref (θ ref (t)) fvco (θ vco (t)), θ ˙ vco = ω vcofree + K vcoc ∗ x. {\ displaystyle {\ begin {array} {ll} {\ dot {x}} = Ax + bf_ {ref} (\ theta _ {ref} (t)) f_ {vco} (\ theta _ {vco} (т)), {\ dot {\ theta}} _ {vco} = \ omega _ {vco} ^ {free} + K_ {vco} c ^ {*} x. \ end {array}}}

{\ displaystyle {\ begin {array} {ll} {\ dot {x}} = Ax + bf_ { ref} (\ theta _ {ref} (t)) f_ {vco} (\ theta _ {vco} (t)), {\ dot {\ theta}} _ {vco} = \ omega _ {vco} ^ {бесплатно} + K_ {vco} c ^ {*} x. \ end {array}}}

Система не автономна и достаточно сложна для исследования.

В фазо-частотной области

Эквивалентная фазово-частотная модель петли Костаса

Вход ГУН для фазово-частотной модели петли Костаса

В простейшем случае, когда

fref (θ ref (t)) = cos ⁡ (ω reft), fvco (θ vco (t)) = sin ⁡ (θ vco (t)) fref (θ ref (t)) 2 fvco (θ vco (t)) fvco (θ vco (t) - π 2) = - 1 8 (2 sin ⁡ (2 θ vco (t)) + sin ⁡ (2 θ vco (t) - 2 ω reft) + sin ⁡ (2 θ vco ( t) + 2 ω reft)) {\ displaystyle {\ begin {align} f_ {ref} {\ big (} \ theta _ {ref} (t) {\ big)} = \ cos {\ big (} \ omega _ {ref} t {\ big)}, \ f_ {vco} {\ big (} \ theta _ {vco} (t) {\ big)} = \ sin {\ big (} \ theta _ {vco} (t) {\ big)} \\ f_ {ref} {\ big (} \ theta _ {ref} (t) {\ big)} ^ {2} f_ {vco} \ left (\ theta _ {vco} (t) \ right) f_ {vco} \ left (\ theta _ {vco} (t) - {\ frac {\ pi} {2}} \ right) = - {\ frac {1} {8}} {\ Big (} 2 \ sin (2 \ theta _ {vco} (t)) + \ sin (2 \ theta _ {vco} (t) -2 \ omega _ {ref} t) + \ sin (2 \ theta _ {vco} (t) +2 \ omega _ {ref} t) {\ Big)} \ end {align}}}

{\ displaystyle {\ begin {align} f_ {ref} {\ big (} \ theta _ {ref} (t) {\ big)} = \ cos {\ big (} \ omega _ {ref } t {\ big)}, \ f_ {vco} {\ big (} \ theta _ {vco} (t) {\ big)} = \ sin {\ big (} \ theta _ {vco} (t) {\ big)} \\ f_ {ref} {\ big (} \ theta _ {ref} (t) {\ big)} ^ {2} f_ {vco} \ left (\ theta _ {vco} (t) \ right) f_ {vco} \ left (\ theta _ {vco} (t) - {\ frac {\ pi} {2}} \ right) = - {\ frac {1} {8}} {\ Big (} 2 \ sin (2 \ theta _ {vco} (t)) + \ sin (2 \ theta _ {vco} (t) -2 \ omega _ {ref} t) + \ sin (2 \ theta _ { vco} (t) +2 \ omega _ {ref} t) {\ Big)} \ end {align}}}

стандартный en Техническое предположение состоит в том, что фильтр удаляет верхнюю боковую полосу с частотой из входа, но оставляет нижнюю боковую полосу без изменений. Таким образом, предполагается, что вход ГУН равен $φ (θ r e f (t) - θ v c o (t)) = 1 8 sin ⁡ (2 ω r e f t - 2 θ v c o (t)). {\ displaystyle \ varphi (\ theta _ {ref} (t) - \ theta _ {vco} (t)) = {\ frac {1} {8}} \ sin (2 \ omega _ {ref} t-2 \ theta _ {vco} (t)).}$ ${\ displaystyle \ varphi (\ theta _ {ref} (t) - \ theta _ {vco} (t)) = {\ frac {1} {8}} \ sin (2 \ om ega _ {ref} t-2 \ theta _ {vco} (t)).}$ Это делает петлю Костаса эквивалентной схеме фазовой автоподстройки частоты с характеристикой фазового детектора $φ (θ) {\ displaystyle \ varphi (\ theta)}$ $\ varphi (\ theta)$ в соответствии с конкретными формами волны $fref (θ) {\ displaystyle f_ {ref} (\ theta)}$ ${\ displaystyle f_ {ref} (\ theta)}$ и $fvco (θ) {\ displaystyle f_ {vco} (\ theta)}$ ${\ displaystyle f_ {vco} (\ theta)}$ входных сигналов и сигналов VCO. Можно доказать, что выходы фильтров во временной области и фазово-частотной области практически равны.

Таким образом, можно изучить более простую автономную систему дифференциальных уравнений

x ˙ = A x + b φ ( Δ θ), Δ θ ˙ = ω vcofree - ω ref + K vcoc ∗ x, Δ θ = θ vco - θ ref. {\ displaystyle {\ begin {align} {\ dot {x}} = Ax + b \ varphi (\ Delta \ theta), \\\ Delta {\ dot {\ theta}} = \ omega _ {vco} ^ {free} - \ omega _ {ref} + K_ {vco} c ^ {*} x, \\\ Delta \ theta = \ theta _ {vco} - \ theta _ {ref}. \ end {выровнено} }}

{\ displa ystyle {\ begin {align} {\ dot {x}} = Ax + b \ varphi (\ Delta \ theta), \\\ Delta {\ dot {\ theta}} = \ omega _ {vco} ^ { бесплатно} - \ omega _ {ref} + K_ {vco} c ^ {*} x, \\\ Delta \ theta = \ theta _ {vco} - \ theta _ {ref}. \ end {align}}}

Метод усреднения Крылова – Боголюбова позволяет доказать близость решений неавтономных и автономных уравнений при некоторых предположениях. Таким образом, блок-схема Costas Loop во временном пространстве может быть асимптотически изменена на блок-схему на уровне фазово-частотных соотношений.

Переход к анализу автономной динамической модели петли Костаса (вместо неавтономной) позволяет преодолеть трудности, связанные с моделированием петли Костаса во временной области, где необходимо одновременно наблюдать очень быстро временная шкала входных сигналов и медленная временная шкала фазы сигнала. Эта идея позволяет рассчитать основные рабочие характеристики - диапазоны удержания, втягивания и захвата.

Получение частоты

Петля Костаса до синхронизации

Петля Костаса после синхронизации

Несущая и сигналы ГУН перед синхронизацией

Вход ГУН во время синхронизации

Сигналы несущей и ГУН после синхронизации

Классическая петля Костаса будет работать для того, чтобы разность фаз между несущей и ГУН стала небольшой, в идеале нулевой величиной. Небольшая разность фаз означает, что синхронизация частоты была достигнута.

Петля Костаса QPSK

Классическая петля Костаса может быть адаптирована к модуляции QPSK для более высоких скоростей передачи данных.

Классическая петля Костаса QPSK

Вход Сигнал QPSK выглядит следующим образом:

m 1 (t) cos ⁡ (ω ref t) + m 2 (t) sin ⁡ (ω ref t), m 1 (t) = ± 1, m 2 (t) = ± 1. {\ Displaystyle m_ {1} (t) \ cos \ left (\ omega _ {\ text {ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ right), m_ {1} (t) = \ pm 1, m_ {2} (t) = \ pm 1.}

{\ displaystyle m_ {1} (t) \ cos \ left (\ omega _ {\ text {ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ справа), m_ {1} (t) = \ pm 1, m_ {2} (t) = \ pm 1.}

Входы фильтров нижних частот LPF1 и LPF2 являются

φ 1 (t) = cos ⁡ (θ vco) (m 1 (t) cos ⁡ (ω ref t) + m 2 (t) sin ⁡ (ω ref t)), φ 2 (t) = sin ⁡ (θ vco) (m 1 (t) cos ⁡ (ω ref t) + m 2 (t) sin ⁡ (ω ref t)). {\ Displaystyle {\ begin {align} \ varphi _ {1} (t) = \ cos \ left (\ theta _ {\ text {vco}} \ right) \ left (m_ {1} (t) \ cos \ left (\ omega _ {\ text {ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ right) \ right), \\ \ varphi _ {2} (t) = \ sin \ left (\ theta _ {\ text {vco}} \ right) \ left (m_ {1} (t) \ cos \ left (\ omega _ {\ text {ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ right) \ right). \ end {align}}}

{ \ Displaystyle {\ begin {align} \ varphi _ {1} (t) = \ cos \ left (\ theta _ {\ text {vco}} \ right) \ left (m_ {1} (t) \ cos \ left (\ omega _ {\ text {ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ right) \ right), \\\ varphi _ {2} (t) = \ sin \ left (\ theta _ {\ text {vco}} \ right) \ left (m_ {1} (t) \ cos \ left (\ omega _ {\ text { ref}} t \ right) + m_ {2} (t) \ sin \ left (\ omega _ {\ text {ref}} t \ right) \ right). \ end {align}}}

После используются выходы синхронизации LPF1 $Q (t) {\ displaystyle Q (t)}$ $Q (t)$ и LPF2 $I (t) {\ displaystyle I (t)}$ $I (t)$ для получения демодулированных данных ( $m 1 (t) {\ displaystyle m_ {1} (t)}$ $m_ {1} (t)$ и $m 2 (t) {\ displaystyle m_ {2} (t)}$ ${\ displaystyle m_ {2} (t)}$ ). Чтобы отрегулировать частоту ГУН частотных сигналов опорных $Q (T) {\ displaystyle Q (T)}$ $Q (t)$ и $Я (т) {\ displaystyle Я (т)}$ $I (t)$ проходит через ограничители и перемножается:

ud (t) = I (t) sgn ⁡ (Q (t)) - Q (t) sgn ⁡ (I (t)). {\ displaystyle u_ {d} (t) = I (t) \ operatorname {sgn} (Q (t)) - Q (t) \ operatorname {sgn} (I (t)).}

{ \ displaystyle u_ {d} (t) = I (t) \ operatorname {sgn} (Q (t)) - Q (t) \ operatorname {sgn} (I (t)).}

После этого сигнала $ud (t) {\ displaystyle u_ {d} (t)}$ ${\ displaystyle u_ {d} (t)}$ фильтруется контурным фильтром и формирует сигнал настройки для VCO $u LF (t) {\ displaystyle u _ {\ text {LF}} (t)}$ ${\ displaystyle u _ {\ text {LF}} (t)}$ аналогично петле Костаса BPSK. Таким образом, QPSK Костаса можно описать системой ОДУ

x ˙ 1 = A LPF x 1 + b LPF φ 1 (t), x ˙ 2 = A LPF x 2 + b LPF φ 2 (t), x ˙ = A LF x + b LF (c LPF ∗ x 1 sign ⁡ (c LPF ∗ x 2) - c LPF ∗ x 2 sign ⁡ (c LPF ∗ x 1)), θ ˙ vco = ω vco free + K VCO ( c LF ∗ x + h (c LPF ∗ x 1 sign ⁡ (c LPF ∗ x 2) - c LPF ∗ x 2 sign ⁡ (c LPF ∗ x 1))). {\ displaystyle {\ begin {align} {\ dot {x}} _ {1} = A _ {\ text {LPF}} x_ {1} + b _ {\ text {LPF}} \ varphi _ {1} ( t), \\ {\ dot {x}} _ {2} = A _ {\ text {LPF}} x_ {2} + b _ {\ text {LPF}} \ varphi _ {2} (t), \ \ {\ dot {x}} = A _ {\ text {LF}} x + b _ {\ text {LF}} \ left (c _ {\ text {LPF}} ^ {*} x_ {1} \ operatorname { sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {2} \ right) -c _ {\ text {LPF}} ^ {*} x_ {2} \ operatorname {sgn} \ left (c_ {\ text {LPF}} ^ {*} x_ {1} \ right) \ right), \\ {\ dot {\ theta}} _ {\ text {vco}} = \ omega _ {\ text {vco }} ^ {\ text {free}} + K _ {\ text {VCO}} \ left (c _ {\ text {LF}} ^ {*} x + h \ left (c _ {\ text {LPF}} ^ { *} x_ {1} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {2} \ right) -c _ {\ text {LPF}} ^ {*} x_ {2} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {1} \ right) \ right) \ right). \\\ end {align}}}

{\ displaystyle {\ begin {align} {\ dot {x}} _ {1} = A _ {\ text {LPF}} x_ {1} + b _ {\ text {LPF }} \ varphi _ {1} (t), \\ {\ dot {x}} _ {2} = A _ {\ text {LPF}} x_ {2} + b _ {\ text {LPF}} \ varphi _ {2} (t), \\ {\ dot {x}} = A _ {\ text {LF}} x + b _ {\ text {LF}} \ left (c _ {\ text {LPF}} ^ { *} x_ {1} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {2} \ right) -c _ {\ text {LPF}} ^ {*} x_ {2} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {1} \ right) \ right), \\ {\ dot {\ theta}} _ {\ text {vco}} = \ omega _ {\ text {vco}} ^ {\ text {free}} + K _ {\ text {VCO}} \ left (c _ {\ text {LF}} ^ {*} x + h \ left (c_ {\ text {LPF}} ^ {*} x_ {1} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {2} \ right) -c _ {\ text {LPF} } ^ {*} x_ {2} \ operatorname {sgn} \ left (c _ {\ text {LPF}} ^ {*} x_ {1} \ right) \ right) \ right). \\\ end {выровнено} }}

Здесь $A LPF, b LPF, c LPF {\ displaystyle A _ {\ text {LPF}}, b _ {\ text {LPF}}, c _ {\ text {LPF}}}$ ${\ displaystyle A_ { \ text {LPF}}, b _ {\ text {LPF}}, c _ {\ text {LPF}}}$ - параметры LPF1 и LPF2 и $A LF, b LF, c LF, h LF {\ displaystyle A _ {\ text {LF}}, b _ {\ text {LF}}, c _ {\ text {LF}}, h _ {\ text { LF}}}$ ${\ displaystyle A _ {\ text {LF}}, b _ {\ text {LF}}, c _ {\ text {LF}}, h _ {\ text {LF}}}$ - параметры петлевого фильтра.

Ссылки

В эту статью включены материалы общественного достояния из документа General Services Administration : «Федеральный стандарт 1037C».