Икосаэдр Джессена

Икосаэдр Джессена
Лица
Края
Вершины	12
Двугранный угол ( градусы )	90
Характеристики
Сеть

Икосаэдр Джессена, иногда называемый ортогональным икосаэдром Джессена, представляет собой невыпуклый многогранник с тем же количеством вершин, ребер и граней, что и правильный икосаэдр. Он назван в честь Бёрге Джессена, изучавшего его в 1967 году. В 1971 году семейство невыпуклых многогранников, включающее эту форму, было независимо открыто и изучено Адриеном Дуади под названием шестиклювый треск ; более поздние авторы применили варианты этого имени более конкретно к икосаэдру Джессена.

Грани икосаэдра Джессена встречаются только под прямым углом, даже если он не имеет ориентации, где все они параллельны координатным плоскостям. Это «шаткий многогранник», означающий, что (как и гибкий многогранник ) он не бесконечно мал. Очерчивание краев этого многогранника распорками и тросами дает широко используемую структуру тенсегрити, также называемую тенсегрити с шестью стержнями, икосаэдром тенсегрити или расширенным октаэдром.

• 1 Строительные и геометрические свойства
• 2 Структурная жесткость
• 3 Связанные формы
• 4 ссылки
• 5 Внешние ссылки

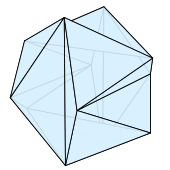Вид с полупрозрачными лицами

Вершины икосаэдра Джессена могут быть выбраны так, чтобы иметь в качестве координат двенадцать троек, заданных циклическими перестановками координат. При таком координатном представлении короткие ребра икосаэдра (с выпуклыми углами) имеют длину, а длинные ребра (рефлекторные) имеют длину. Гранями икосаэдра являются восемь конгруэнтных равносторонних треугольников с короткой стороной и двенадцать конгруэнтных тупоугольных равнобедренных треугольников с одним длинным ребром и двумя короткими ребрами. ${\ Displaystyle (\ ч 2, \ ч 1,0)}$${\ displaystyle {\ sqrt {6}}}$${\ Displaystyle 4}$

Икосаэдр Джессена является вершинно-транзитивным (или изогональным), что означает, что он имеет симметрии, переводящие любую вершину в любую другую вершину. Его двугранные углы прямые. Его можно использовать как основу для построения бесконечного семейства комбинаторно различных многогранников с прямыми двугранными углами, образованных путем склеивания копий икосаэдра Джессена вместе на их равносторонних треугольных гранях.

Как и в случае с более простым многогранником Шёнхардта, внутреннюю часть икосаэдра Джессена нельзя триангулировать в тетраэдры без добавления новых вершин. Однако, поскольку его двугранные углы являются рациональными кратными,${\ Displaystyle \ пи}$ он имеет инвариант Дена, равный нулю. Следовательно, он конгруэнтен кубу как ножницы, а это означает, что его можно разрезать на более мелкие многогранные части, которые можно переставить, чтобы сформировать цельный куб.

Он имеет форму звезды, что означает, что внутри него есть точка (например, его центр симметрии), из которой видны все остальные точки. Он представляет собой контрпример к вопросу Мишеля Демазюра о том, можно ли сделать звездообразные многогранники с треугольными гранями выпуклыми, сдвинув их вершины по лучам из этой центральной точки. Демазюр связал этот вопрос с одним пунктом алгебраической геометрии, доказав, что для звездчатых многогранников с треугольными гранями определенное алгебраическое многообразие, связанное с многогранником, было бы проективным многообразием, если бы многогранник можно было сделать выпуклым таким образом. Однако Адриен Дуади доказал, что для семейства форм, включающего икосаэдр Джессена, это скользящее движение не может привести к выпуклому многограннику. Демазюр использовал этот результат для построения непроективного гладкого рационального полного трехмерного многообразия.

Het Ding  [ nl ], скульптура тенсегрити, стойки и тросы которой образуют контур икосаэдра Джессена, в Университете Твенте.

Икосаэдр Джессена не является гибким многогранником : если его грани построены из жестких панелей, соединенных шарнирами, он не может изменить форму. Однако она также не является бесконечно жесткой. Это означает, что существует непрерывное движение его вершин, которое на самом деле не сохраняет длины ребер и формы граней многогранника, но делает это в приближении первого порядка. Как жесткий, но не бесконечно жесткий многогранник, он образует пример «шаткого многогранника». Поскольку очень небольшие изменения длин его ребер могут вызвать гораздо большие изменения его углов, физические модели многогранника кажутся гибкими.

Замена длинных вогнуто-двугранных ребер икосаэдра Джессена жесткими распорками, а более коротких выпукло-двугранных ребер кабелями или проводами приводит к созданию тенсегрити - структуры, которую также называют «шестигранным тенсегрити», «тенсегрити-икосаэдром» или «тенсегрити-икосаэдром». расширенный октаэдр». Как и в скульптурах тенсегрити, эта структура является «наиболее распространенной формой тенсегрити-роботов», а детская игрушка «Сквиш», основанная на этой структуре, была «распространена в 1980-х годах». Концепция «супершарового бота», основанная на этой конструкции, была предложена Институтом передовых концепций НАСА как способ ограждения устройств для исследования космоса для безопасных посадок на другие планеты. Энтони Пью называет эту структуру «возможно, самой известной и, безусловно, одной из самых впечатляющих фигур тенсегрити».

Икосаэдр Джессена слабо выпуклый, что означает, что его вершины находятся в выпуклом положении, и его существование демонстрирует, что слабо выпуклые многогранники не обязательно должны быть бесконечно жесткими. Однако была высказана гипотеза, что триангулируемые слабо выпуклые многогранники должны быть бесконечно мало жесткими, и эта гипотеза была доказана при дополнительном предположении, что внешняя часть выпуклой оболочки многогранника также может быть триангулирована.

Правильный икосаэдр и его невыпуклый вариант, который отличается от икосаэдра Джессена другим положением вершин и непрямоугольными двугранниками.

Аналогичную форму можно получить, сохранив вершины правильного икосаэдра в исходных положениях и заменив некоторые пары равносторонних треугольников парами равнобедренных треугольников. Эту форму также иногда ошибочно называют икосаэдром Джессена. Однако, хотя полученный многогранник имеет ту же комбинаторную структуру и симметрию, что и икосаэдр Джессена, и выглядит похоже, он не образует тенсегрити-структуры и не имеет прямоугольных двугранников.

Икосаэдр Джессена является одним из непрерывного семейства икосаэдров с 20 гранями, 8 из которых являются равносторонними треугольниками и 12 из которых являются равнобедренными треугольниками. Каждая форма в этом семействе получается из правильного октаэдра путем деления каждого из его ребер в одинаковой пропорции и соединения точек деления по образцу правильного икосаэдра. Эти формы могут быть параметризованы пропорцией, на которую разделены ребра октаэдра. Выпуклые формы в этом семействе варьируются от самого октаэдра через правильный икосаэдр до кубооктаэдра с его квадратными гранями, разделенными на два прямоугольных треугольника в плоской плоскости. Расширение диапазона параметра за пропорцию, которая дает кубооктаэдр, дает невыпуклые формы, включая икосаэдр Джессена. Это семейство было описано Х.С.М. Коксетером в 1947 году. Позже скручивающие, расширяюще-сжимающие преобразования между членами этого семейства, параметризованные по-разному, чтобы поддерживать постоянное значение для одной из двух длин ребер, были названы Бакминстером Фуллером преобразованиями Jitterbug.

В 2018 г. икосаэдр Джессена был обобщен В.А. Горькавым и А.Д. Милкой  [ uk ] на бесконечное семейство жестких, но не бесконечно малых жестких многогранников. Эти многогранники комбинаторно различны и имеют киральные диэдральные группы симметрии сколь угодно большого порядка. Однако, в отличие от икосаэдра Джессена, не все их грани являются треугольниками.

• Ортогональный икосаэдр Джессена, Мир многогранников, Морис Старк; включает в себя 3D-модель, которую можно просматривать с произвольной ориентации