Тотальная функция Эйлера

"φ (n)" перенаправляется сюда. Чтобы узнать о других значениях, см. Phi. Первая тысяча значений φ ( n). Точки на верхней строке представляют φ ( p), когда p - простое число, то есть p - 1.

В теории чисел, Функция Эйлер подсчитывает положительные целые числа до заданного целого числа п, которые взаимно просты с п. Он пишется с использованием греческой буквы фи как или, и может также называться функцией фи Эйлера. Другими словами, это количество целых чисел к в диапазоне 1 ≤ K ≤ N, для которых наибольший общий делитель НОД ( п, к) равно 1. целые числа к этой формы иногда называют totatives из п. ${\ Displaystyle \ varphi (п)}$${\ Displaystyle \ фи (п)}$

Например, сумма n = 9 - это шесть чисел 1, 2, 4, 5, 7 и 8. Все они взаимно просты с 9, но три других числа в этом диапазоне, 3, 6 и 9, не являются., так как gcd (9, 3) = gcd (9, 6) = 3 и gcd (9, 9) = 9. Следовательно, φ (9) = 6. Другой пример: φ (1) = 1, поскольку для n = 1 единственное целое число в диапазоне от 1 до n - это 1, а НОД (1, 1) = 1.

Функция Эйлера является мультипликативной функцией, что означает, что если два числа m и n взаимно просты, то φ ( mn) = φ ( m) φ ( n). Данная функция выдает приказ о мультипликативной группе целых чисел по модулю п (The группы из единиц в кольце ). Он также используется для определения системы шифрования RSA. ${\ Displaystyle \ mathbb {Z} / п \ mathbb {Z}}$

• 1 История, терминология и обозначения
• 2 Вычисление тотентифицирующей функции Эйлера
  • 2.1 Формула произведения Эйлера
    • 2.1.1 Phi - мультипликативная функция
    • 2.1.2 Значение phi для аргумента мощности простого числа
    • 2.1.3 Доказательство формулы произведения Эйлера
    • 2.1.4 Пример
  • 2.2 преобразование Фурье
  • 2.3 Сумма делителя
• 3 Некоторые значения
• 4 Теорема Эйлера
• 5 Другие формулы
  • 5.1 личность Менона
  • 5.2 Формулы, содержащие золотое сечение
• 6 Генерирующие функции
• 7 Скорость роста
• 8 Соотношение последовательных значений
• 9 номеров Totient
  • 9.1 Теорема Форда
  • 9.2 Совершенные общие числа
• 10 приложений
  • 10.1 Циклотомия
  • 10.2 Криптосистема RSA
• 11 нерешенных проблем
  • 11.1 Гипотеза Лемера
  • 11.2 Гипотеза Кармайкла
• 12 См. Также
• 13 Примечания
• 14 Ссылки
• 15 Внешние ссылки

Леонард Эйлер ввел эту функцию в 1763 году. Однако в то время он не выбрал какой-либо конкретный символ для ее обозначения. В публикации 1784 года Эйлер дополнительно изучил функцию, выбрав для ее обозначения греческую букву π: он написал πD для «множества чисел меньше D, не имеющих с ним общего делителя». Это определение отличается от текущего определения функции totient при D = 1, но в остальном остается таким же. Ныне стандартное обозначение φ ( A) взято из трактата Гаусса 1801 г. Disquisitiones Arithmeticae, хотя Гаусс не использовал круглые скобки вокруг аргумента и написал φA. Таким образом, ее часто называют phi-функцией Эйлера или просто phi-функцией.

В 1879 году, JJ Сильвестр ввел термин totient для этой функции, поэтому его называют также функцией Эйлера totient, в Эйлере totient или Эйлер в. Тотиент Джордана является обобщением теории Эйлера.

Cototient из п определяется как п - ф ( п). Он подсчитывает количество положительных целых чисел, меньших или равных n, у которых есть хотя бы один простой делитель, общий с n.

Есть несколько формул для вычисления φ ( n).

Формула произведения Эйлера

Говорится

${\ displaystyle \ varphi (n) = n \ prod _ {p \ mid n} \ left (1 - {\ frac {1} {p}} \ right),}$

где произведение находится над различными простыми числами, делящими n. (Обозначения см. В разделе Арифметическая функция. )

Эквивалентная формулировка для, где - различные простые числа, делящие n:${\ displaystyle n = p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ {r} ^ {k_ {r}}}$${\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {r}}$

$${\ displaystyle \ varphi (n) = p_ {1} ^ {k_ {1} -1} (p_ {1} {-} 1) \, p_ {2} ^ {k_ {2} -1} (p_ { 2} {-} 1) \ cdots p_ {r} ^ {k_ {r} -1} (p_ {r} {-} 1).}$$ Доказательство этих формул зависит от двух важных фактов.

Phi - мультипликативная функция

Это означает, что если gcd ( m, n) = 1, то φ ( m) φ ( n) = φ ( mn). Схема доказательства: пусть A, B, C - множества натуральных чисел, взаимно простых с m, n, mn и меньших, чем m, n, mn, соответственно, так что | А | = φ ( m) и т. д. Тогда существует биекция между A × B и C по китайской теореме об остатках.

Значение фи для аргумента первичной мощности

Если p простое и k ≥ 1, то

${\ displaystyle \ varphi \ left (p ^ {k} \ right) = p ^ {k} -p ^ {k-1} = p ^ {k-1} (p-1) = p ^ {k} \ left (1 - {\ tfrac {1} {p}} \ right).}$

Доказательство: поскольку p - простое число, единственными возможными значениями gcd ( p ^k, m) являются 1, p, p ²,..., p ^k, и это единственный способ иметь gcd ( p ^k, m)gt; 1 означает, что m кратно p, то есть m = p, 2 p, 3 p,..., p ^{k - 1}p = p ^k, и таких кратных p ^{k - 1} меньше, чем p ^k. Следовательно, все остальные p ^k - p ^{k - 1} числа взаимно просты с p ^k.

Доказательство формулы произведения Эйлера

Основная теорема арифметических состояний, что если п gt; 1 существует единственное выражение, где р 1 lt; р 2 lt;... lt; р г являются простыми числами, и каждый к я ≥ 1. (Случай n = 1 соответствует пустому произведению.) Многократное использование мультипликативного свойства φ и формулы для φ ( p ^k) дает ${\ displaystyle n = p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ {r} ^ {k_ {r}},}$

${\ displaystyle {\ begin {array} {rcl} \ varphi (n) amp; = amp; \ varphi (p_ {1} ^ {k_ {1}}) \, \ varphi (p_ {2} ^ {k_ {2}) }) \ cdots \ varphi (p_ {r} ^ {k_ {r}}) \\ [. 1em] amp; = amp; p_ {1} ^ {k_ {1} -1} (p_ {1} -1) \, p_ {2} ^ {k_ {2} -1} (p_ {2} -1) \ cdots p_ {r} ^ {k_ {r} -1} (p_ {r} -1) \\ [. 1em] amp; = amp; p_ {1} ^ {k_ {1}} \ left (1 - {\ frac {1} {p_ {1}}} \ right) p_ {2} ^ {k_ {2}} \ left (1- {\ frac {1} {p_ {2}}} \ right) \ cdots p_ {r} ^ {k_ {r}} \ left (1 - {\ frac {1} {p_ {r}}} \ right) \\ [. 1em] amp; = amp; p_ {1} ^ {k_ {1}} p_ {2} ^ {k_ {2}} \ cdots p_ {r} ^ {k_ {r}} \ left (1 - {\ frac {1} {p_ {1}}} \ right) \ left (1 - {\ frac {1} {p_ {2}}} \ right) \ cdots \ left (1 - {\ frac {1} {p_ {r}}} \ right) \\ [. 1em] amp; = amp; n \ left (1 - {\ frac {1} {p_ {1}}} \ right) \ left (1 - {\ frac {1} { p_ {2}}} \ right) \ cdots \ left (1 - {\ frac {1} {p_ {r}}} \ right). \ end {array}}}$

Это дает обе версии формулы произведения Эйлера.

Альтернативное доказательство, которое не требует мультипликативного свойства, вместо этого использует принцип включения-исключения, примененный к множеству, исключая множества целых чисел, делящихся на простые делители. ${\ Displaystyle \ {1,2, \ ldots, п \}}$

Пример

${\ Displaystyle \ varphi (20) = \ varphi (2 ^ {2} 5) = 20 \, (1 - {\ tfrac {1} {2}}) \, (1 - {\ tfrac {1} {5 }}) = 20 \ cdot {\ tfrac {1} {2}} \ cdot {\ tfrac {4} {5}} = 8.}$

На словах: различные простые делители числа 20 равны 2 и 5; половина из двадцати целых чисел от 1 до 20 делится на 2, остается десять; пятая часть из них делится на 5, в результате чего восемь чисел взаимно просты с 20; это: 1, 3, 7, 9, 11, 13, 17, 19.

Альтернативная формула использует только целые числа:

$${\ displaystyle \ varphi (20) = \ varphi (2 ^ {2} 5 ^ {1}) = 2 ^ {2-1} (2 {-} 1) \, 5 ^ {1-1} (5 { -} 1) = 2 \ cdot 1 \ cdot 1 \ cdot 4 = 8.}$$

преобразование Фурье

Totient является дискретным преобразованием Фурье от НОДА, оценивается в 1. Пусть

${\ Displaystyle {\ mathcal {F}} \ {\ mathbf {x} \} [m] = \ sum \ limits _ {k = 1} ^ {n} x_ {k} \ cdot e ^ {{- 2 \ пи i} {\ frac {mk} {n}}}}$

где x k = gcd ( k, n) для k ∈ {1,..., n }. потом

${\ displaystyle \ varphi (n) = {\ mathcal {F}} \ {\ mathbf {x} \} [1] = \ sum \ limits _ {k = 1} ^ {n} \ gcd (k, n) e ^ {- 2 \ pi i {\ frac {k} {n}}}.}$

Действительная часть этой формулы

${\ displaystyle \ varphi (n) = \ sum \ limits _ {k = 1} ^ {n} \ gcd (k, n) \ cos {\ tfrac {2 \ pi k} {n}}.}$

Например, используя и:${\ displaystyle \ cos {\ tfrac {\ pi} {5}} = {\ tfrac {{\ sqrt {5}} + 1} {4}}}$${\ displaystyle \ cos {\ tfrac {2 \ pi} {5}} = {\ tfrac {{\ sqrt {5}} - 1} {4}}}$

$${\ Displaystyle {\ begin {array} {rcl} \ varphi (10) amp; = amp; \ gcd (1,10) \ cos {\ tfrac {2 \ pi} {10}} + \ gcd (2,10) \ cos {\ tfrac {4 \ pi} {10}} + \ gcd (3,10) \ cos {\ tfrac {6 \ pi} {10}} + \ cdots + \ gcd (10,10) \ cos {\ tfrac {20 \ pi} {10}} \\ amp; = amp; 1 \ cdot ({\ tfrac {{\ sqrt {5}} + 1} {4}}) + 2 \ cdot ({\ tfrac {{\ sqrt { 5}} - 1} {4}}) + 1 \ cdot (- {\ tfrac {{\ sqrt {5}} - 1} {4}}) + 2 \ cdot (- {\ tfrac {{\ sqrt { 5}} + 1} {4}}) + 5 \ cdot (-1) \\ amp;amp; + \ 2 \ cdot (- {\ tfrac {{\ sqrt {5}} + 1} {4}}) + 1 \ cdot (- {\ tfrac {{\ sqrt {5}} - 1} {4}}) + 2 \ cdot ({\ tfrac {{\ sqrt {5}} - 1} {4}}) + 1 \ cdot ({\ tfrac {{\ sqrt {5}} + 1} {4}}) + 10 \ cdot (1) \\ amp; = amp; 4. \ end {array}}}$$ В отличие от произведения Эйлера и формулы суммы делителей, здесь не требуется знать множители n. Однако он включает в себя вычисление наибольшего общего делителя n и каждого положительного целого числа меньше n, что в любом случае достаточно для факторизации.

Сумма делителя

Установленное Гауссом свойство

${\ displaystyle \ sum _ {d \ mid n} \ varphi (d) = n,}$

где сумма берется по всем положительным делителям d числа n, можно доказать несколькими способами. (См. Условные обозначения в разделе Арифметическая функция. )

Одно из доказательств состоит в том, чтобы отметить, что φ ( d) также равно количеству возможных образующих циклической группы C d  ; В частности, если С д = ⟨ г ⟩ с г ^д = 1, то г ^к представляет собой генератор для каждого к взаимно просто д. Поскольку каждый элемент C n порождает циклическую подгруппу, а все подгруппы C d ⊆ C n порождаются в точности φ ( d) элементами C n, формула следует. Эквивалентно, формула может быть получена с помощью того же аргумента, примененного к мультипликативной группе корней n- й степени из единицы и примитивных корнях d- й степени из единицы.

Формулу можно также получить из элементарной арифметики. Например, пусть n = 20 и рассмотрим положительные дроби до 1 со знаминателем 20:

${\ displaystyle {\ tfrac {1} {20}}, \, {\ tfrac {2} {20}}, \, {\ tfrac {3} {20}}, \, {\ tfrac {4} {20 }}, \, {\ tfrac {5} {20}}, \, {\ tfrac {6} {20}}, \, {\ tfrac {7} {20}}, \, {\ tfrac {8} {20}}, \, {\ tfrac {9} {20}}, \, {\ tfrac {10} {20}}, \, {\ tfrac {11} {20}}, \, {\ tfrac { 12} {20}}, \, {\ tfrac {13} {20}}, \, {\ tfrac {14} {20}}, \, {\ tfrac {15} {20}}, \, {\ tfrac {16} {20}}, \, {\ tfrac {17} {20}}, \, {\ tfrac {18} {20}}, \, {\ tfrac {19} {20}}, \, {\ tfrac {20} {20}}.}$

Поместите их в самые низкие термины:

${\ displaystyle {\ tfrac {1} {20}}, \, {\ tfrac {1} {10}}, \, {\ tfrac {3} {20}}, \, {\ tfrac {1} {5 }}, \, {\ tfrac {1} {4}}, \, {\ tfrac {3} {10}}, \, {\ tfrac {7} {20}}, \, {\ tfrac {2} {5}}, \, {\ tfrac {9} {20}}, \, {\ tfrac {1} {2}}, \, {\ tfrac {11} {20}}, \, {\ tfrac { 3} {5}}, \, {\ tfrac {13} {20}}, \, {\ tfrac {7} {10}}, \, {\ tfrac {3} {4}}, \, {\ tfrac {4} {5}}, \, {\ tfrac {17} {20}}, \, {\ tfrac {9} {10}}, \, {\ tfrac {19} {20}}, \, {\ tfrac {1} {1}}}$

Эти двадцать фракций все положительные k/d≤ 1, знаменателями которого являются делители d = 1, 2, 4, 5, 10, 20. Дроби со знаменателем 20 - это дроби, числители которых взаимно просты с 20, а именно:1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20; по определению это дроби φ (20). Аналогичным образом, существует ф (10) фракции с знаменателем 10, и ф (5) дроби с знаменателем 5 и т.д. Таким образом, множество из двадцати фракций разделяются на подмножества размера ф ( г) для каждого д делящихся 20. Аналогичного рассуждения применяется для любого n.

Обращение Мёбиуса, примененное к формуле суммы делителей, дает

${\ displaystyle \ varphi (n) = \ sum _ {d \ mid n} \ mu \ left (d \ right) \ cdot {\ frac {n} {d}} = n \ sum _ {d \ mid n} {\ frac {\ mu (d)} {d}},}$

где μ - функция Мёбиуса, мультипликативная функция, определяемая и для каждого простого числа p и k ≥ 1. Эта формула также может быть получена из формулы произведения путем умножения, чтобы получить${\ displaystyle \ mu (p) = - 1}$${\ displaystyle \ mu (p ^ {k}) = 0}$${\ textstyle \ prod _ {p \ mid n} (1 - {\ frac {1} {p}})}$${\ textstyle \ sum _ {d \ mid n} {\ frac {\ mu (d)} {d}}.}$

Пример:

$${\ Displaystyle {\ begin {выровнено} \ varphi (20) amp; = \ mu (1) \ cdot 20+ \ mu (2) \ cdot 10+ \ mu (4) \ cdot 5+ \ mu (5) \ cdot 4+ \ mu (10) \ cdot 2+ \ mu (20) \ cdot 1 \\ [. 5em] amp; = 1 \ cdot 20-1 \ cdot 10 + 0 \ cdot 5-1 \ cdot 4 + 1 \ cdot 2 + 0 \ cdot 1 = 8. \ End {align}}}$$

Первые 100 значений (последовательность A000010 в OEIS ) показаны в таблице и на графике ниже:

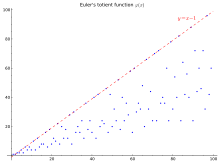
График первых 100 значений

φ ( n) для 1 ≤ n ≤ 100

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28 год	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28 год	58	16
60	60	30	36	32	48	20	66	32	44 год	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44 год	60	46	72	32	96	42	60	40

На графике справа верхняя линия y = n - 1 является верхней границей, действительной для всех n, кроме одного, и достигается тогда и только тогда, когда n - простое число. Простая нижняя граница есть, которая довольно нечеткая: на самом деле нижняя граница графика пропорциональна${\ displaystyle \ varphi (п) \ geq {\ sqrt {n / 2}}}$ п/журнал журнал n.

Основная статья: теорема Эйлера

Это утверждает, что если и п являются взаимно простыми, то

${\ Displaystyle a ^ {\ varphi (n)} \ Equiv 1 \ mod n.}$

Частный случай, когда n простое, известен как малая теорема Ферма.

Это следует из теоремы Лагранжа и тот факт, что φ ( п) является порядок в мультипликативной группе целых чисел по модулю п.

RSA криптосистемы на основе этой теоремы: это означает, что обратная функции ↦ ^е мод п, где е является (общественного) шифрования показатель, функция б ↦ б ^д мод п, где г, тем (частное) показатель расшифровки является мультипликативным обратным к e по модулю φ ( n). Таким образом, сложность вычисления φ ( n) без знания факторизации n является сложностью вычисления d: это известно как проблема RSA, которая может быть решена путем факторизации n. Владелец закрытого ключа знает факторизацию, поскольку закрытый ключ RSA создается путем выбора n как произведения двух (случайно выбранных) больших простых чисел p и q. Публично раскрывается только n, и, учитывая сложность факторизации больших чисел, у нас есть гарантия, что никто другой не знает факторизации.

• ${\ displaystyle a \ mid b \ подразумевает \ varphi (a) \ mid \ varphi (b)}$
• ${\ displaystyle n \ mid \ varphi (a ^ {n} -1) \ quad {\ text {for}} a, ngt; 1}$
• ${\ displaystyle \ varphi (mn) = \ varphi (m) \ varphi (n) \ cdot {\ frac {d} {\ varphi (d)}} \ quad {\ text {where}} d = \ operatorname {gcd } (m, n)}$

  Обратите внимание на особые случаи

  • ${\ displaystyle \ varphi (2m) = {\ begin {case} 2 \ varphi (m) amp; {\ text {if}} m {\ text {четно}} \\\ varphi (m) amp; {\ text { if}} m {\ text {нечетное}} \ end {case}}}$
  • ${\ displaystyle \ varphi \ left (п ^ {m} \ right) = n ^ {m-1} \ varphi (n)}$
• ${\ displaystyle \ varphi (\ operatorname {lcm} (m, n)) \ cdot \ varphi (\ operatorname {gcd} (m, n)) = \ varphi (m) \ cdot \ varphi (n)}$

  Сравните это с формулой

  • ${\ displaystyle \ operatorname {lcm} (m, n) \ cdot \ operatorname {gcd} (m, n) = m \ cdot n}$
  (См. Наименьшее общее кратное. )
• φ ( n) четно при n ≥ 3. Более того, если n имеет r различных нечетных простых множителей, 2 ^r | φ ( п)
• Для любых a gt; 1 и n gt; 6 таких, что 4 ∤ n, существует l ≥ 2 n такое, что l | φ ( a ⁿ - 1).
• ${\ displaystyle {\ frac {\ varphi (n)} {n}} = {\ frac {\ varphi (\ operatorname {rad} (n))} {\ operatorname {rad} (n)}}}$

  где rad ( n) - радикал числа n (произведение всех различных простых чисел, делящих n ).

• ${\ displaystyle \ sum _ {d \ mid n} {\ frac {\ mu ^ {2} (d)} {\ varphi (d)}} = {\ frac {n} {\ varphi (n)}}}$ 
• ${\ Displaystyle \ сумма _ {1 \ Leq к \ Leq п \ на вершине (к, п) = 1} \! \! к = {\ tfrac {1} {2}} п \ varphi (п) \ квад {\ текст {for}} ngt; 1}$
• ${\ displaystyle \ sum _ {k = 1} ^ {n} \ varphi (k) = {\ tfrac {1} {2}} \ left (1+ \ sum _ {k = 1} ^ {n} \ mu (k) \ left \ lfloor {\ frac {n} {k}} \ right \ rfloor ^ {2} \ right) = {\ frac {3} {\ pi ^ {2}}} n ^ {2} + O \ left (n (\ log n) ^ {\ frac {2} {3}} (\ log \ log n) ^ {\ frac {4} {3}} \ right)}$ (цитируется в)
• ${\ displaystyle \ sum _ {k = 1} ^ {n} {\ frac {\ varphi (k)} {k}} = \ sum _ {k = 1} ^ {n} {\ frac {\ mu (k)} {k}} \ left \ lfloor {\ frac {n} {k}} \ right \ rfloor = {\ frac {6} {\ pi ^ {2}}} n + O \ left ((\ log n) ^ {\ frac {2} {3}} (\ log \ log n) ^ {\ frac {4} {3}} \ right)}$ 
• ${\ displaystyle \ sum _ {k = 1} ^ {n} {\ frac {k} {\ varphi (k)}} = {\ frac {315 \, \ zeta (3)} {2 \ pi ^ {4 }}} n - {\ frac {\ log n} {2}} + O \ left ((\ log n) ^ {\ frac {2} {3}} \ right)}$ 
• ${\ displaystyle \ sum _ {k = 1} ^ {n} {\ frac {1} {\ varphi (k)}} = {\ frac {315 \, \ zeta (3)} {2 \ pi ^ {4 }}} \ left (\ log n + \ gamma - \ sum _ {p {\ text {prime}}} {\ frac {\ log p} {p ^ {2} -p + 1}} \ right) + O \ left ({\ frac {(\ log n) ^ {\ frac {2} {3}}} {n}} \ right)}$

  (где γ - постоянная Эйлера – Маскерони ).

• ${\ displaystyle \ sum _ {\ stackrel {1 \ leq k \ leq n} {\ operatorname {gcd} (k, m) = 1}} \! \! \! \! 1 = n {\ frac {\ varphi (m)} {m}} + O \ left (2 ^ {\ omega (m)} \ right)}$

  где m gt; 1 - натуральное число, а ω ( m) - количество различных простых делителей числа m.

Личность Менона

Основная статья: личность Менона

В 1965 г. П. Кесава Менон доказал, что

${\ Displaystyle \ сумма _ {\ stackrel {1 \ leq k \ leq n} {\ gcd (k, n) = 1}} \! \! \! \! \ gcd (k-1, n) = \ varphi (n) d (n),}$

где d ( n) = σ 0 ( n) - количество делителей числа n.

Формулы с золотым сечением

Шнайдер обнаружил пару тождеств, соединяющих функцию totient, золотое сечение и функцию Мёбиуса μ ( n). В этом разделе φ ( n) - функция тотализатора, а ϕ =1 + √ 5/2= 1,618... золотое сечение.

Они есть:

${\ displaystyle \ phi = - \ sum _ {k = 1} ^ {\ infty} {\ frac {\ varphi (k)} {k}} \ log \ left (1 - {\ frac {1} {\ phi ^ {k}}} \ right)}$

а также

${\ displaystyle {\ frac {1} {\ phi}} = - \ sum _ {k = 1} ^ {\ infty} {\ frac {\ mu (k)} {k}} \ log \ left (1- {\ frac {1} {\ phi ^ {k}}} \ right).}$

Их вычитание дает

${\ displaystyle \ sum _ {k = 1} ^ {\ infty} {\ frac {\ mu (k) - \ varphi (k)} {k}} \ log \ left (1 - {\ frac {1} { \ phi ^ {k}}} \ right) = 1.}$

Применение экспоненциальной функции к обеим сторонам предыдущего тождества дает формулу бесконечного произведения для e :

${\ displaystyle e = \ prod _ {k = 1} ^ {\ infty} \ left (1 - {\ frac {1} {\ phi ^ {k}}} \ right) \! \! ^ {\ frac { \ mu (k) - \ varphi (k)} {k}}.}$

Доказательство основано на двух формулах

${\ displaystyle {\ begin {align} \ sum _ {k = 1} ^ {\ infty} {\ frac {\ varphi (k)} {k}} \ left (- \ log \ left (1-x ^ { k} \ right) \ right) amp; = {\ frac {x} {1-x}} \\ {\ text {and}} \; \ sum _ {k = 1} ^ {\ infty} {\ frac { \ mu (k)} {k}} \ left (- \ log \ left (1-x ^ {k} \ right) \ right) amp; = x, \ qquad \ quad {\ text {for}} 0 lt;x lt;1. \ конец {выровнено}}}$

Ряд Дирихле для ф ( п) можно записать в терминах дзета - функции Римана, как:

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {\ varphi (n)} {n ^ {s}}} = {\ frac {\ zeta (s-1)} {\ zeta (s)}}.}$

Серии Ламберта производящей функцией является

${\ displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {\ varphi (n) q ^ {n}} {1-q ^ {n}}} = {\ frac {q} {( 1-q) ^ {2}}}}$

который сходится при | q | lt;1.

Оба эти утверждения доказываются манипуляциями с элементарными рядами и формулами для φ ( n).

По словам Харди и Райта, порядок φ ( n) «всегда почти n ».

Первый

${\ displaystyle \ lim \ sup {\ frac {\ varphi (n)} {n}} = 1,}$

но когда n стремится к бесконечности, для всех δ gt; 0

${\ displaystyle {\ frac {\ varphi (n)} {n ^ {1- \ delta}}} \ rightarrow \ infty.}$

Эти две формулы можно доказать, используя немногим больше, чем формулы для φ ( n) и функции суммы делителей σ ( n).

Фактически при доказательстве второй формулы неравенство

${\ displaystyle {\ frac {6} {\ pi ^ {2}}} lt;{\ frac {\ varphi (n) \ sigma (n)} {n ^ {2}}} lt;1,}$

верно для n gt; 1, доказано.

У нас также есть

${\ displaystyle \ lim \ inf {\ frac {\ varphi (n)} {n}} \ log \ log n = e ^ {- \ gamma}.}$

Здесь γ является постоянная Эйлера, γ = 0,577215665..., поэтому е ^γ = 1.7810724... и е ^{- γ} = 0.56145948....

Доказательство этого не совсем требует теоремы о простых числах. Поскольку log log n стремится к бесконечности, эта формула показывает, что

${\ displaystyle \ lim \ inf {\ frac {\ varphi (n)} {n}} = 0.}$

На самом деле, правда больше.

${\ displaystyle \ varphi (n)gt; {\ frac {n} {e ^ {\ gamma} \; \ log \ log n + {\ frac {3} {\ log \ log n}}}} \ quad {\ text {for}} ngt; 2}$

а также

${\ displaystyle \ varphi (n) lt;{\ frac {n} {e ^ {\ gamma} \ log \ log n}} \ quad {\ text {для бесконечного числа}} n.}$

Второе неравенство показал Жан-Луи Николя. Рибенбойм говорит: «Метод доказательства интересен тем, что неравенство показано, во-первых, в предположении, что гипотеза Римана верна, а во-вторых, в противоположном предположении».

Для среднего заказа имеем

${\ displaystyle \ varphi (1) + \ varphi (2) + \ cdots + \ varphi (n) = {\ frac {3n ^ {2}} {\ pi ^ {2}}} + O \ left (n ( \ log n) ^ {\ frac {2} {3}} (\ log \ log n) ^ {\ frac {4} {3}} \ right) \ quad {\ text {as}} n \ rightarrow \ infty,}$

благодаря Арнольду Вальфизу, в его доказательстве используются оценки экспоненциальных сумм, полученные И. М. Виноградовым и Н. М. Коробовым (в настоящее время это наиболее известная оценка такого типа). «Большой O » обозначает количество, которое ограничено константой, кратной функции п внутри круглых скобок (которая мала по сравнению с п ²).

Этот результат может быть использован для доказательства того, что вероятность того, что два случайно выбранных числа будут относительно простыми, равна 6/π ².

В 1950 году Сомаяджулу доказал, что

${\ displaystyle {\ begin {align} \ lim \ inf {\ frac {\ varphi (n + 1)} {\ varphi (n)}} amp; = 0 \ quad {\ text {and}} \\ [5px] \ lim \ sup {\ frac {\ varphi (n + 1)} {\ varphi (n)}} amp; = \ infty. \ end {align}}}$

В 1954 году Шинцель и Серпинский усилили это, доказав, что набор

${\ displaystyle \ left \ {{\ frac {\ varphi (n + 1)} {\ varphi (n)}}, \; \; n = 1,2, \ ldots \ right \}}$

является плотным в положительных действительных чисел. Они также доказали, что множество

${\ displaystyle \ left \ {{\ frac {\ varphi (n)} {n}}, \; \; n = 1,2, \ ldots \ right \}}$

плотно в интервале (0,1).

Номер totient является значением Функция Эйлера: то есть, т, для которых имеется по меньшей мере один п, для которых ф ( п) = т. Валентность или кратность из числа totient т есть число решений этого уравнения. Нетотиентное число представляет собой натуральное число, которое не является числом totient. Каждое нечетное целое число, превышающее 1, тривиально неточность. Существует также бесконечно много четных не значащих элементов, и действительно, каждое положительное целое число имеет кратное, которое не является четным.

Количество общих чисел до заданного предела x равно

${\ displaystyle {\ frac {x} {\ log x}} e ^ {\ big (} C + o (1) {\ big)} (\ log \ log \ log x) ^ {2}}}$

для постоянной C = 0.8178146....

Если считать по кратности, количество общих чисел до заданного предела x равно

${\ displaystyle {\ Big \ vert} \ {n: \ varphi (n) \ leq x \} {\ Big \ vert} = {\ frac {\ zeta (2) \ zeta (3)} {\ zeta (6)}} \ cdot x + R (x)}$

где погрешность R порядка не болееИкс/(журнал x) ^kдля любого положительного k.

Известно, что кратность m бесконечно часто превышает m ^δ при любом δ lt;0,55655.

Теорема Форда

Форд (1999) доказал, что для любого целого числа k ≥ 2 существует общее число m кратности k: то есть, для которого уравнение φ ( n) = m имеет ровно k решений; этот результат был ранее высказали предположение по Серпинскому, и оно было получено в результате Шинцель в гипотезе H. В самом деле, каждая возникающая множественность происходит бесконечно часто.

Однако неизвестно число m с кратностью k = 1. Гипотеза Кармайкла о тотализирующей функции - это утверждение, что такой m не существует.

Идеальные общие числа

Основная статья: Идеальное число

Циклотомия

Основная статья: Конструируемый многоугольник

В последнем разделе « Исследований» Гаусс доказывает, что правильный n -угольник можно построить с помощью линейки и циркуля, если φ ( n) является степенью 2. Если n является степенью нечетного простого числа, формула для totient говорит, что его totient может быть степенью двойки, только если n - первая степень, а n - 1 - степень 2. Простые числа, которые на единицу больше, чем степень двойки, называются простыми числами Ферма, и известны только пять: 3, 5, 17, 257 и 65537. Ферма и Гаусс знали об этом. Никто не смог доказать, есть ли еще.

Таким образом, правильный n -угольник имеет конструкцию линейки и циркуля, если n является произведением различных простых чисел Ферма и любой степени 2. Первые несколько таких n равны

2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40,... (последовательность A003401 в OEIS ).

Криптосистема RSA

Основная статья: RSA (алгоритм)

Настройка системы RSA включает выбор больших простых чисел p и q, вычисление n = pq и k = φ ( n) и нахождение двух чисел e и d, таких что ed ≡ 1 (mod k). Числа n и e («ключ шифрования») публикуются, а d («ключ дешифрования») остается закрытым.

Сообщение, представленное целым числом m, где 0 lt; m lt; n, шифруется путем вычисления S = m ^e (mod n).

Он расшифровывается путем вычисления t = S ^d (mod n). Теорема Эйлера может быть использована, чтобы показать, что если 0 lt; t lt; n, то t = m.

Безопасность системы RSA будет поставлена ​​под угрозу, если число n может быть разложено на множители или если φ ( n) может быть вычислен без факторизации n.

Гипотеза Лемера

Основная статья: проблема Лемера

Если p простое, то φ ( p) = p - 1. В 1932 году Д.Х. Лемер спросил, существуют ли какие-нибудь составные числа n такие, что φ ( n) делит n - 1. Никто не известен.

В 1933 году он доказал, что если такое n существует, оно должно быть нечетным, бесквадратным и делимым не менее чем на семь простых чисел (т.е. ω ( n) ≥ 7). В 1980 году Коэн и Хагис доказали, что n gt; 10 ²⁰ и ω ( n) ≥ 14. Далее Хагис показал, что если 3 делит n, то n gt; 10 ^1937042 и ω ( n) ≥ 298848.

Гипотеза Кармайкла

Основная статья: Гипотеза тотентифицирующей функции Кармайкла

Это заявляет, что нет никакого числа п с тем свойством, что для всех остальных чисел т, т ≠ п, ф ( т) ≠ ф ( п). См. Теорему Форда выше.

Как указано в основной статье, если существует единственный контрпример к этой гипотезе, должно быть бесконечно много контрпримеров, а самый маленький из них имеет не менее десяти миллиардов цифр в базе 10.

• Функция Кармайкла
• Гипотеза Даффина – Шеффера
• Обобщения малой теоремы Ферма
• Сильно составное число
• Мультипликативная группа целых чисел по модулю n
• Рамануджанская сумма
• Тотент-сумматорная функция
• Пси-функция Дедекинда

" Disquisitiones Arithmeticae" переведена с латыни на английский и немецкий языки. Немецкое издание включает все работы Гаусса по теории чисел: все доказательства квадратичной взаимности, определение знака суммы Гаусса, исследования биквадратичной взаимности и неопубликованные заметки.

Ссылки на Disquisitiones имеют форму Gauss, DA, art. nnn.

• Абрамовиц, М. ; Стегун, И. А. (1964), Справочник по математическим функциям, Нью-Йорк: Dover Publications, ISBN   0-486-61272-4. См. Параграф 24.3.2.
• Бах, Эрик ; Шаллит, Джеффри (1996), теория алгоритмических чисел (том I: эффективные алгоритмы), серия MIT Press по основам вычислений, Кембридж, Массачусетс: The MIT Press, ISBN   0-262-02405-5, Zbl   0873,11070
• Диксон, Леонард Юджин, «История теории чисел», том 1, глава 5 «Функция Эйлера, обобщения; ряд Фарея», Chelsea Publishing, 1952 г.
• Форд, Кевин (1999), "Количество решений ф ( х) =  т ", Анналы математики, 150 (1): 283-311, DOI : 10,2307 / 121103, ISSN   0003-486X, JSTOR   121103, МР   1715326, Zbl   0978,11053.
• Гаусс, Карл Фридрих ; Кларк, Артур А. (переводчик на английский язык) (1986), Disquisitiones Arithmeticae (второе, исправленное издание), Нью-Йорк: Springer, ISBN   0-387-96254-9
• Гаусс, Карл Фридрих ; Мазер, Х. (перевод на немецкий) (1965), Untersuchungen uber hohere Arithmetik (Disquisitiones Arithmeticae и другие статьи по теории чисел) (второе издание), Нью-Йорк: Челси, ISBN   0-8284-0191-8
• Грэм, Рональд ; Кнут, Дональд ; Паташник, Орен (1994), Конкретная математика : основа информатики (2-е изд.), Ридинг, Массачусетс: Аддисон-Уэсли, ISBN   0-201-55802-5, Zbl   0836,00001
• Гай, Ричард К. (2004), Нерешенные проблемы теории чисел, Проблемные книги по математике (3-е изд.), Нью-Йорк, Нью-Йорк: Springer-Verlag, ISBN   0-387-20860-7, Zbl   1058,11001
• Харди, GH ; Райт, EM (1979), Введение в теорию чисел (пятое изд.), Oxford: Oxford University Press, ISBN   978-0-19-853171-5
• Лонг, Кальвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Lexington: DC Heath and Company, LCCN   77-171950
• Петтофреццо, Энтони Дж.; Биркит, Дональд Р. (1970), Элементы теории чисел, Englewood Cliffs: Prentice Hall, LCCN   77-81766
• Рибенбойм, Пауло (1996), Новая книга рекордов простых чисел (3-е изд.), Нью-Йорк: Springer, ISBN   0-387-94457-5, Zbl   0856,11001
• Сандифер, Чарльз (2007), Ранняя математика Леонарда Эйлера, MAA, ISBN   0-88385-559-3
• Шандор, Йожеф; Mitrinović, Dragoslav S.; Crstici, Борислав, ред. (2006), Справочник по теории чисел I, Дордрехт: Springer-Verlag, стр. 9–36, ISBN   1-4020-4215-9, Zbl   1151,11300
• Шандор, Йожеф; Crstici, Борислав (2004). Справочник по теории чисел II. Дордрехт: Kluwer Academic. стр.  179 -327. ISBN   1-4020-2546-7. Zbl   1079.11001.
• Шрамм, Вольфганг (2008), "Преобразование Фурье функций наибольшего общего делителя", Электронный журнал комбинаторной теории чисел, A50 (8 (1)).

• "Totient function", Энциклопедия математики, EMS Press, 2001 [1994]
• Фи-функция Эйлера и китайская теорема об остатках - доказательство мультипликативности φ ( n)
• Калькулятор функции Эйлера в JavaScript - до 20 цифр
• Динева, Розика, Тотиент Эйлера, Мёбиуса и функции делителя
• Плитадж, Лумис, Полхилл, подводя итоги функции Эйлера-Фи