Изометрия евклидовой плоскости

В геометрии изометрия евклидовой плоскости - это изометрия евклидовой плоскости, или, более неформально, способ преобразования плоскости, сохраняющий геометрические свойства, такие как длина. Существует четыре типа: смещения, вращения, отражения и отражения скольжения (см. Ниже в разделе классификация изометрий евклидовой плоскости ).

Набор изометрий евклидовой плоскости образует группу в рамках композиции : евклидова группа в двух измерениях. Он создается отражениями в линиях, и каждый элемент евклидовой группы является составной частью не более трех различных отражений.

• 1 Неформальное обсуждение
• 2 Формальное определение
• 3 Классификация
  • 3.1 Отражения
  • 3.2 Перевод
  • 3.3 Вращения
  • 3.4 Жесткие трансформации
  • 3.5 Скользящие отражения
• 4 Изометрии как группа отражений
  • 4.1 Комбинации зеркал
  • 4.2 Достаточно трех зеркал
  • 4.3 Распознавание
  • 4.4 Групповая структура
  • 4.5 Состав
  • 4.6 Смещение, вращение и ортогональные подгруппы
  • 4.7 Построение вложенных групп
  • 4.8 Дискретные подгруппы
• 5 Изометрии в комплексной плоскости
• 6 См. Также
• 7 Ссылки
• 8 Внешние ссылки

Неформально, евклидово Изометрия плоскости - это любой способ преобразования плоскости без ее "деформации". Например, предположим, что евклидова плоскость представлена ​​листом прозрачного пластика, лежащим на столе. Примеры изометрии:

• Сдвиг листа на один дюйм вправо.
• Поворот листа на десять градусов вокруг отмеченной точки (которая остается неподвижной).
• Переворачивание листа на посмотри на это сзади. Обратите внимание, что если изображение нарисовано на одной стороне листа, то после переворота листа мы видим зеркальное отображение изображения.

Это примеры переводов, вращения и отражения соответственно. Существует еще один тип изометрии, называемый отражением скольжения (см. Ниже в разделе классификация изометрий евклидовой плоскости ).

Однако складывание, разрезание или плавление листа не считаются изометрией. Нет и менее радикальных изменений, таких как сгибание, растяжение или скручивание.

изометрия евклидовой плоскости - это преобразование плоскости с сохранением расстояния. То есть это карта

$M:\; R\; 2\; \to \; R\; 2\; \{\backslash \; displaystyle\; M:\; \{\backslash \; textbf\; \{R\}\}\; ^\; \{2\}\; \backslash \; to\; \{\backslash \; textbf\; \{R\}\}\; ^\; \{2\}\}$

такая, что для любых точек p и q на плоскости

$d\; (p,\; q)\; =\; d\; (M\; (p),\; M\; (q)),\; \{\backslash \; displaystyle\; d\; (p,\; q)\; =\; d\; (\; M\; (p),\; M\; (q)),\}$

где d (p, q) - обычное евклидово расстояние между p и q.

Можно показать, что существует четыре типа изометрий евклидовой плоскости. (Примечание : обозначения для типов изометрий, перечисленных ниже, не полностью стандартизированы.)

Отражения

Отражения или зеркальные изометрии, обозначенные F c, v, где c - точка на плоскости, а v - единичный вектор в R . (F означает «перевернуть».) Иметь эффект отражения точки p на прямой L, которая перпендикулярна v и проходит через c. Линия L называется осью отражения или соответствующим зеркалом . Чтобы найти формулу для F c, v, мы сначала используем скалярное произведение, чтобы найти компонент t числа p - c в направлении v,

$t\; =\; (p\; -\; c)\; \cdot \; v\; =\; (px\; -\; cx)\; vx\; +\; (py\; -\; cy)\; vy,\; \{\backslash \; displaystyle\; t\; =\; (pc)\; \backslash \; cdot\; v\; =\; (p\_\; \{x\}\; -c\_\; \{x\})\; v\_\; \{x\}\; +\; (p\_\; \{\; y\}\; -c\_\; \{y\})\; v\_\; \{y\},\}$

и затем мы получаем отражение p путем вычитания,

$F\; c,\; v\; (p)\; =\; p\; -\; 2\; tv.\; \{\backslash \; displaystyle\; F\_\; \{c,\; v\}\; (p)\; =\; p-2tv.\}$

Комбинация поворотов вокруг начала координат и отражений относительно линии, проходящей через начало координат, получается со всеми ортогональными матрицами (то есть с определителем 1 и −1), образующие ортогональную группу O (2). В случае определителя −1 имеем:

$R\; 0,\; \theta \; (p)\; =\; (cos\; \; \theta \; sin\; \; \theta \; sin\; \; \theta \; -\; cos\; \; \theta )\; [p\; x\; p\; y].\; \{\backslash \; Displaystyle\; R\_\; \{0,\; \backslash \; theta\}\; (p)\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; cos\; \backslash \; theta\; \backslash \; sin\; \backslash \; theta\; \backslash \backslash \backslash \; sin\; \backslash \; theta\; -\; \backslash \; cos\; \backslash \; theta\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; p\_\; \{x\}\; \backslash \backslash \; p\_\; \{y\}\; \backslash \; end\; \{bmatrix\}\}.\}$

который является отражением по оси x, за которым следует поворот на угол θ, или, что то же самое, отражение в линии образуя угол θ / 2 с осью x. Отражение на параллельной прямой соответствует добавлению вектора, перпендикулярного ей.

Переводы

Переводы, обозначаемые T v, где v - вектор в R имеют эффект сдвига плоскости в направлении v. То есть для любой точки p на плоскости

$T\; v\; (p)\; =\; p\; +\; v,\; \{\backslash \; displaystyle\; T\_\; \{v\}\; (p)\; =\; p\; +\; v,\}$

или в терминах координат (x, y)

$T\; v\; (p)\; =\; [px\; +\; vxpy\; +\; vy].\; \{\backslash \; displaystyle\; T\_\; \{v\}\; (p)\; =\; \{\backslash \; begin\; \{bmatrix\}\; p\_\; \{x\}\; +\; v\_\; \{x\}\; \backslash \backslash \; p\_\; \{y\}\; +\; v\_\; \{y\}\; \backslash \; end\; \{bmatrix\}\}.\}$

Перевод можно рассматривать как композицию двух параллельных отражений.

Вращения

Вращение, обозначается R c, θ, где c - точка на плоскости (центр вращения), θ - угол поворота. В терминах координат вращения проще всего выразить, разбив их на две операции. Во-первых, поворот вокруг начала координат задается как

$R\; 0,\; \theta \; (p)\; =\; (cos\; \; \theta \; -\; sin\; \; \theta \; sin\; \; \theta \; cos\; \; \theta )\; [p\; x\; p\; y].\; \{\backslash \; Displaystyle\; R\_\; \{0,\; \backslash \; theta\}\; (p)\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; cos\; \backslash \; theta\; -\; \backslash \; sin\; \backslash \; theta\; \backslash \backslash \backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; theta\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; p\_\; \{x\}\; \backslash \backslash \; p\_\; \{y\}\; \backslash \; end\; \{bmatrix\}\}.\}$

Эти матрицы являются ортогональными матрицами (т.е. каждая представляет собой квадратную матрицу G, транспонирование - это его обратный, то есть $GGT\; =\; GTG\; =\; I\; 2.\; \{\backslash \; Displaystyle\; GG\; ^\; \{T\}\; =\; G\; ^\; \{T\}\; G\; =\; I\_\; \{2\}.\}$) с определителем 1 (другая возможность для ортогональных матриц - −1, что дает зеркальное отображение, см. Ниже). Они образуют специальную ортогональную группу SO (2).

Вращение вокруг c может быть выполнено сначала путем перевода c в начало координат, затем выполнения поворота вокруг начала координат и, наконец, перевода начала координат обратно в начало координат. c. То есть

$R\; c,\; \theta \; =\; T\; c\; \circ \; R\; 0,\; \theta \; \circ \; T\; -\; c,\; \{\backslash \; displaystyle\; R\_\; \{c,\; \backslash \; theta\}\; =\; T\_\; \{c\}\; \backslash \; circ\; R\_\; \{0,\; \backslash \; theta\}\; \backslash \; circ\; T\_\; \{-c\},\}$

или, другими словами,

$R\; c,\; \theta \; (p)\; =\; c\; +\; R\; 0,\; \theta \; (p\; -\; c).\; \{\backslash \; displaystyle\; R\_\; \{c,\; \backslash \; theta\}\; (p)\; =\; c\; +\; R\_\; \{0,\; \backslash \; theta\}\; (pc).\}$

В качестве альтернативы выполняется вращение вокруг начала координат с последующим переводом:

$R\; c,\; \theta \; (p)\; =\; c\; -\; R\; 0,\; \theta \; c\; +\; R\; 0,\; \theta \; (p).\; \{\backslash \; displaystyle\; R\_\; \{c,\; \backslash \; theta\}\; (p)\; =\; c-R\_\; \{0,\; \backslash \; theta\}\; c\; +\; R\_\; \{0,\; \backslash \; theta\}\; (p).\}$

Поворот можно рассматривать как соединение двух непараллельные отражения.

Жесткие преобразования

Набор перемещений и вращений вместе образуют жесткие движения или жесткие перемещения . Этот набор образует группу по композиции, группу жестких движений, подгруппу полной группы евклидовых изометрий.

Отражения при скольжении

Отражения при скольжении, обозначаемые G c, v, w, где c - точка на плоскости, v является единичным вектором в R, и w не равно нулю; вектор, перпендикулярный v, представляет собой комбинацию отражения в линии, описанной c и v, с последующим перемещением вдоль w. То есть

$G\; c,\; v,\; w\; =\; T\; w\; \circ \; F\; c,\; v,\; \{\backslash \; displaystyle\; G\_\; \{c,\; v,\; w\}\; =\; T\_\; \{w\}\; \backslash \; circ\; F\_\; \{c,\; v\},\}$

или другими словами,

$G\; c,\; v,\; w\; (p)\; =\; w\; +\; F\; c,\; v\; (p).\; \{\backslash \; Displaystyle\; G\_\; \{c,\; v,\; w\}\; (p)\; =\; w\; +\; F\_\; \{c,\; v\}\; (p).\}$

(Также верно, что

$G\; c,\; v,\; w\; (p)\; =\; F\; c,\; v\; (p\; +\; w);\; \{\backslash \; displaystyle\; G\_\; \{c,\; v,\; w\}\; (p)\; =\; F\_\; \{c,\; v\}\; (p\; +\; w);\}$

то есть мы получаем тот же результат, если мы выполняем перенос и отражение в обратном порядке.)

В качестве альтернативы мы умножаем на ортогональную матрицу с определителем −1 (соответствует отражению в линии, проходящей через начало координат), после чего следует перенос. Это скользящее отражение, за исключением особого случая, когда перенос перпендикулярен линии отражения, и в этом случае комбинация сама по себе является просто отражением в параллельной линии.

идентичность изометрия, определяемый как I (p) = p для всех точек p, является частным случаем сдвига, а также частным случаем вращения. Это единственная изометрия, которая принадлежит более чем к одному из описанных выше типов.

Во всех случаях мы умножаем вектор положения на ортогональную матрицу и добавляем вектор; если определитель равен 1, у нас есть вращение, сдвиг или идентичность, а если он равен -1, у нас есть скользящее отражение или отражение.

«Случайная» изометрия, такая как взятие листа бумаги со стола и его случайное отложение, «почти наверняка » - это вращение или скользящее отражение (у них три степени свободы ). Это применяется независимо от деталей распределения вероятностей, пока θ и направление добавленного вектора независимы и равномерно распределены, а длина добавленный вектор имеет непрерывное распределение. Чистый перевод и чистое отражение - это особые случаи с двумя степенями свободы, в то время как тождество еще более особенное, без степеней свободы.

Отражения или зеркальные изометрии можно комбинировать для получения любой изометрии. Таким образом, изометрии являются примером группы отражений .

Комбинации зеркал

В евклидовой плоскости у нас есть следующие возможности.

• [d] Идентичность

Два отражения в одном и том же зеркале восстанавливают каждую точку в исходное положение. Все точки оставлены фиксированными. Любая пара одинаковых зеркал имеет одинаковый эффект.

• [db] Отражение

Как Алиса обнаружила через зеркало, одно зеркало заставляет левую и правую руки переключаться. (Формально топологическая ориентация меняется на противоположную.) Точки на зеркале остаются неподвижными. Каждое зеркало имеет уникальный эффект.

• [dp] Вращение

Два различных пересекающихся зеркала имеют одну общую точку, которая остается неизменной. Все остальные точки вращаются вокруг него на угол, вдвое больший между зеркалами. Любые два зеркала с одинаковой фиксированной точкой и одинаковым углом дают одно и то же вращение, если они используются в правильном порядке.

• [dd] Перевод

Два разных зеркала, которые не пересекаются, должны быть параллельны. Каждая точка перемещается на одинаковое расстояние, вдвое большее расстояние между зеркалами, и в одном направлении. Точки не остаются неподвижными. Любые два зеркала с одинаковым параллельным направлением и одинаковым расстоянием друг от друга дают одинаковое перемещение, если они используются в правильном порядке.

• [dq] Скользящее отражение

Три зеркала. Если все они параллельны, эффект будет таким же, как у одного зеркала (сдвиньте пару, чтобы отменить третье). В противном случае мы можем найти эквивалентное расположение, где два параллельны, а третье перпендикулярно им. Эффект представляет собой отражение в сочетании с перемещением параллельно зеркалу. Точки не остаются фиксированными.

Достаточно трех зеркал

Добавление большего количества зеркал не добавляет больше возможностей (в плоскости), потому что их всегда можно переставить, чтобы вызвать отмену.

Доказательство . Изометрия полностью определяется ее воздействием на три независимых (не коллинеарных) точки. Итак, предположим, что p 1, p 2, p 3 отображаются в q 1, q 2, q 3 ; мы можем сгенерировать последовательность зеркал, чтобы добиться этого следующим образом. Если p 1 и q 1 различны, выберите их серединный перпендикуляр как зеркало. Теперь p 1 отображается в q 1 ; и мы пропустим все дальнейшие зеркала через q 1, оставив его фиксированным. Назовите изображения p 2 и p 3 под этим отражением p 2 ′ и p 3 ′. Если q 2 отличается от p 2 ′, разделите угол при q 1 пополам с помощью нового зеркала. Теперь, когда p 1 и p 2, p 3 находится в p 3 ′ ′; и если он не на месте, последнее зеркало через q 1 и q 2 перевернет его на q 3. Таким образом, для воспроизведения любой изометрии плоскости достаточно не более трех отражений. ∎

Распознавание

Мы можем распознать, какая из этих изометрий у нас есть, в зависимости от того, сохраняет ли она руки или меняет их местами, и имеет ли она хотя бы одну фиксированную точку или нет, как показано в следующей таблице (без личность).

Структура группы

Изометрии, требующие нечетного количества зеркала - отражение и скользящее отражение - всегда меняют местами левое и правое. Равные изометрии - идентичность, вращение и перенос - никогда не действуют; они соответствуют жестким движениям и образуют нормальную подгруппу полной евклидовой группы изометрий. Ни полная группа, ни четная подгруппа не являются абелевыми ; например, изменение порядка расположения двух параллельных зеркал на противоположное приводит к изменению направления производимого ими перемещения.

Доказательство . Тождество - это изометрия; ничего не меняется, поэтому расстояние не может измениться. И если одна изометрия не может изменить расстояние, то две (или три, или более) подряд не могут; таким образом, композиция двух изометрий снова является изометрией, а набор изометрий замкнут относительно композиции. Изометрия идентичности также является идентичностью для композиции, и композиция является ассоциативной ; следовательно, изометрии удовлетворяют аксиомам полугруппы . Для группы мы также должны иметь инверсию для каждого элемента. Чтобы отменить отражение, мы просто компилируем его с собой. (Отражения - это инволюции.) И поскольку каждая изометрия может быть выражена как последовательность отражений, ее обратная последовательность может быть выражена как обратная последовательность. Обратите внимание на то, что подавление пары идентичных отражений уменьшает количество отражений на четное число, сохраняя четность последовательности; также обратите внимание, что идентичность имеет четность. Следовательно, все изометрии образуют группу, и даже изометрии - подгруппу. (Нечетные изометрии не включают тождество, поэтому не являются подгруппой.) Эта подгруппа является нормальной подгруппой, потому что размещение четной изометрии между двумя нечетными дает четную изометрию. ∎

Поскольку четная подгруппа нормальна, это ядро ​​ гомоморфизма к фактор-группе, где фактор-группа изоморфна группе, состоящей отражения и идентичности. Однако полная группа не является прямым продуктом, а только полупрямым продуктом четной подгруппы и факторгруппы.

Состав

Композиция изометрий смешивает виды различными способами. Мы можем думать об идентичности либо как о двух зеркалах, либо как об их отсутствии; в любом случае это не влияет на композицию. И два отражения дают либо сдвиг, либо поворот, либо тождество (тривиально и то и другое). Отражение, составленное из любого из них, может сводиться к единственному отражению; в противном случае он дает единственную доступную изометрию с тремя зеркалами - скользящее отражение. Пара переводов всегда сводится к одному переводу; так что сложные случаи связаны с ротацией. Мы знаем, что вращение, состоящее из вращения или смещения, должно давать ровную изометрию. Композиция с перемещением производит другое вращение (на ту же величину, со смещенной фиксированной точкой), но композиция с вращением может давать либо смещение, либо вращение. Часто говорят, что композиция двух вращений производит вращение, и Эйлер доказал теорему на этот счет в 3D; однако это верно только для вращений с общей фиксированной точкой.

Подгруппы смещения, вращения и ортогональности

Таким образом, у нас есть два новых вида подгрупп изометрии: все смещения и повороты с общей фиксированной точкой. Обе являются подгруппами четной подгруппы, внутри которой переводы нормальны. Поскольку трансляции являются нормальной подгруппой, мы можем выделить их, оставив подгруппу изометрий с фиксированной точкой, ортогональную группу .

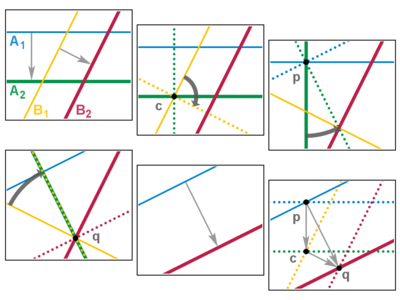
Доказательство . Если два поворота разделяют фиксированную точку, то мы можем повернуть зеркальную пару второго поворота, чтобы отменить внутренние зеркала последовательности из четырех (два и два), оставив только внешнюю пару. Таким образом, сочетание двух вращений с общей фиксированной точкой дает поворот на сумму углов относительно одной и той же фиксированной точки.

Если два перемещения параллельны, мы можем сдвинуть зеркальную пару второго перемещения, чтобы отменить внутреннее зеркало последовательности из четырех, как и в случае вращения. Таким образом, комбинация двух параллельных перемещений дает перенос на сумму расстояний в одном и том же направлении. Теперь предположим, что переводы не параллельны, и что зеркальная последовательность - это A 1, A 2 (первый перевод), за которым следует B 1, B 2 (второй). Тогда A 2 и B 1 должны пересечься, скажем, в c; и, воссоединившись, мы можем повернуть эту внутреннюю пару вокруг c. Если мы повернемся на 90 °, произойдет интересная вещь: теперь A 1 и A 2 ′ пересекаются под углом 90 °, скажем в точке p, и то же самое происходит с B 1 ′ и B 2, скажем, в q. Снова сопоставляя, мы поворачиваем первую пару вокруг p, чтобы B 2 ″ проходили через q, и поворачиваем вторую пару вокруг q, чтобы заставить A 1 ″ проходить через p. Внутренние зеркала теперь совпадают и отменяются, а внешние зеркала остаются параллельными. Таким образом, сочетание двух непараллельных переводов также дает перевод. Кроме того, три точки поворота образуют треугольник, края которого соответствуют правилу «голова к хвосту» сложения векторов : 2 (p c) + 2 (c q) = 2 (p q). ∎

Построение вложенной группы

Структура подгруппы предлагает другой способ составления произвольной изометрии:

Выберите фиксированную точку и зеркало через нее.

1. Если изометрия нечетная, используйте зеркало; в противном случае не делайте этого.
2. Если необходимо, поверните вокруг фиксированной точки.
3. Если необходимо, выполните перевод.

Это работает, потому что переводы являются нормальной подгруппой полной группы изометрий с частным ортогональная группа; и повороты вокруг неподвижной точки являются нормальной подгруппой ортогональной группы с фактором одного отражения.

Дискретные подгруппы

Обсуждаемые до сих пор подгруппы не только бесконечны, но и непрерывны (группы Ли ). Любая подгруппа, содержащая хотя бы один ненулевой перенос, должна быть бесконечной, но подгруппы ортогональной группы могут быть конечными. Например, симметрии правильного пятиугольника состоят из вращений на целые кратные 72 ° (360 ° / 5), а также отражения в пяти зеркалах, которые перпендикулярно делят края пополам. Это группа D 5 с 10 элементами. Он имеет подгруппу C 5 половинного размера, без учета отражений. Эти две группы являются членами двух семейств, D n и C n, для любого n>1. Вместе эти семейства составляют группы розеток ..

Переводы не сворачиваются сами по себе, но мы можем взять целые числа, кратные любому конечному перемещению, или суммы, кратные двум таким независимым переводам, в качестве подгруппы. Они генерируют решетку периодического мозаичного покрытия плоскости.

Мы также можем комбинировать эти два вида дискретных групп - дискретные вращения и отражения вокруг фиксированной точки и дискретные перемещения - для создания групп фризов и групп обоев. Любопытно, что только некоторые из групп фиксированной точки оказались совместимыми с дискретными переводами. Фактически, совместимость решеток налагает такие серьезные ограничения, что вплоть до изоморфизма у нас есть только 7 различных групп фризов и 17 различных групп обоев. Например, симметрии пятиугольника D 5 несовместимы с дискретной решеткой трансляций. (Каждое более высокое измерение также имеет только конечное число таких кристаллографических групп, но их количество быстро растет; например, в 3D есть 230 групп, а в 4D - 4783.)

В терминах комплексных чисел изометрии плоскости имеют форму

$C\; ⟶\; C\; z\; \mapsto \; a\; +\; \omega \; z\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{ccc\}\; \backslash \; mathbb\; \{C\}\; \backslash \; longrightarrow\; \backslash \; mathbb\; \{C\}\; \backslash \backslash \; z\; \backslash \; mapsto\; a\; +\; \backslash \; omega\; z\; \backslash \; end\; \{array\}\}$

или в форме

$C\; ⟶\; C\; z\; \mapsto \; a\; +\; \omega \; z\; ¯,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{ccc\}\; \backslash \; mathbb\; \{C\}\; \backslash \; longrightarrow\; \backslash \; mathbb\; \{C\}\; \backslash \backslash \; z\; \backslash \; mapsto\; a\; +\; \backslash \; omega\; \{\backslash \; overline\; \{z\}\}\; \{\backslash \; t\_dv\; \{,\; \}\}\; \backslash \; end\; \{array\}\}\}$

для некоторых комплексных чисел a и ω с | ω | = 1. Это легко доказать: если a = f (0) и ω = f (1) - f (0) и если определить

$g:\; C\; ⟶\; C\; z\; \mapsto \; f\; (z)\; -\; a\; \omega ,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{array\}\; \{rccc\}\; g\; \backslash \; двоеточие\; \backslash \; mathbb\; \{C\}\; \backslash \; longrightarrow\; \backslash \; mathbb\; \{C\}\; \backslash \backslash \; z\; \backslash \; mapsto\; \{\backslash \; frac\; \{f\; (z)\; -a\}\; \{\backslash \; omega\; \}\}\; \{\backslash \; t\_dv\; \{,\}\}\; \backslash \; end\; \{array\}\}\}$

тогда g - изометрия, g (0) = 0 и g (1) = 1. Тогда легко увидеть, что g либо тождество или сопряжение, и доказываемое утверждение следует из этого и из того, что f (z) = a + ωg (z).

Очевидно, это связано с предыдущей классификацией плоских изометрий, так как:

• функции типа z → a + z являются переводами;
• функции типа z → ωz являются вращениями (когда | ω | = 1);
• сопряжение является отражением.

Обратите внимание, что поворот вокруг комплексной точки p получается комплексной арифметикой с

$z\; \mapsto \; \omega \; (z\; -\; p)\; +\; p\; =\; \omega \; z\; +\; p\; (1\; -\; \omega )\; \{\backslash \; displaystyle\; z\; \backslash \; mapsto\; \backslash \; omega\; (zp)\; +\; p\; =\; \backslash \; omega\; z\; +\; p\; (1-\; \backslash \; omega)\}$

где последнее выражение показывает отображение, эквивалентное вращению при 0 и перевод. Следовательно, по прямой изометрии $z\; \mapsto \; \omega \; z\; +\; a,\; \{\backslash \; displaystyle\; z\; \backslash \; mapsto\; \backslash \; omega\; z\; +\; a,\}$можно решить $p\; (1\; -\; \omega )\; =\; a\; \{\backslash \; displaystyle\; p\; (1-\; \backslash \; omega)\; =\; a\}$, чтобы получить $p\; =\; a\; /\; (1\; -\; \omega )\; \{\backslash \; displaystyle\; p\; =\; a\; /\; (1-\; \backslash \; omega)\}$в качестве центра эквивалентного вращения при условии, что $\omega \; \ne \; 1\; \{\backslash \; displaystyle\; \backslash \; omega\; \backslash \; neq\; 1\}$, то есть при условии, что прямая изометрия не является чистым переносом. Как заявил Седерберг, «Прямая изометрия - это либо вращение, либо перенос».

• теорема Бекмана – Куорлза, характеристика изометрий как преобразований, сохраняющих единичные расстояния
• Конгруэнтность (геометрия)
• Координатные вращения и отражения
• Теорема Ельмслева, утверждение, что середины соответствующих пар точек в изометрии линий коллинеарны

• Изометрия плоскости