Степени свободы (физика и химия)

В физике и химии, a степень свободы - это независимый физический параметр в формальном описании состояния физической системы. Набор всех состояний системы известен как фазовое пространство системы, а степени свободы системы - это измерения фазового пространства.

Расположение частицы в трехмерном пространстве требует трех координат положения. Точно так же направление и скорость, с которой движется частица, можно описать с помощью трех компонентов скорости, каждая из которых относится к трем измерениям пространства. Если временная эволюция системы детерминирована, когда состояние в один момент однозначно определяет ее прошлое и будущее положение и скорость как функцию времени, такая система имеет шесть степеней свободы. Если движение частицы ограничено меньшим числом измерений - например, частица должна двигаться по проводу или по фиксированной поверхности - тогда система имеет менее шести степеней свободы. С другой стороны, система с протяженным объектом, который может вращаться или вибрировать, может иметь более шести степеней свободы.

В классической механике состояние точечной частицы в любой момент времени часто описывается координатами положения и скорости в лагранжевом формализме., или с координатами положения и импульса в формализме гамильтониана.

В статистической механике степень свободы - это единственное скалярное число, описывающее микросостояние системы. Спецификация всех микросостояний системы - это точка в фазовом пространстве системы.

В трехмерной модели идеальной цепи в химии, два угла необходимы для описания ориентация каждого мономера.

Часто бывает полезно указать квадратичные степени свободы. Это степени свободы, которые вносят квадратичный вклад в энергию системы.

Содержание

• 1 Молекулы газа
• 2 Независимые степени свободы
• 3 Квадратичные степени свободы
  • 3.1 Квадратичные и независимые степени свободы
  • 3.2 Теорема о равнораспределении
• 4 Обобщения
• 5 Ссылки

Молекулы газа

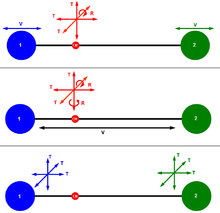Различные способы визуализации 6 степеней свободы двухатомной молекулы. (CM: центр масс системы, T: поступательное движение, R: вращательное движение, V: колебательное движение.)

в трех -мерное пространство, три степени свободы связаны с движением частицы. Двухатомная молекула газа имеет 6 степеней свободы. Этот набор может быть разложен на переводы, вращения и колебания молекулы.Движение центра масс всей молекулы составляет 3 степени свободы. Кроме того, молекула имеет две вращательные степени движения и одну колебательную моду.. Вращения происходят вокруг двух осей, перпендикулярных линии между двумя атомами. Вращение вокруг связи атом-атом не является физическим вращением. Это дает для двухатомной молекулы разложение:

$N\; =\; 6\; =\; 3\; +\; 2\; +\; 1.\; \{\backslash \; Displaystyle\; N\; =\; 6\; =\; 3\; +\; 2\; +\; 1.\}$

Для общей нелинейной молекулы учитываются все 3 степени свободы вращения, в результате получается разложение:

$3\; N\; =\; 3\; +\; 3\; +\; (3\; N\; -\; 6)\; \{\backslash \; displaystyle\; 3N\; =\; 3\; +\; 3\; +\; (3N-6)\}$

, что означает, что молекула N-атома имеет 3N - 6 колебательных степеней свободы для N>2. В особых случаях, таких как адсорбированные большие молекулы, вращательные степени свободы могут быть ограничены только одной.

Как определено выше, можно также подсчитывать степени свободы, используя минимальное количество координат, требуемых для определения положения. Это делается следующим образом:

1. Для отдельной частицы нам нужны 2 координаты в 2-D плоскости, чтобы указать ее положение, и 3 координаты в 3-м пространстве. Таким образом, его степень свободы в трехмерном пространстве равна 3.
2. Для тела, состоящего из двух частиц (например, двухатомной молекулы) в трехмерном пространстве с постоянным расстоянием между ними (скажем, d) мы можем показать (ниже), что его степени свободы равны 5.

Допустим, одна частица в этом теле имеет координаты (x 1, y 1, z 1), а другой имеет координаты (x 2, y 2, z 2), где z 2 неизвестно. Применение формулы для расстояния между двумя координатами

$d\; =\; (x\; 2\; -\; x\; 1)\; 2\; +\; (y\; 2\; -\; y\; 1)\; 2\; +\; (z\; 2\; -\; z\; 1)\; 2\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; sqrt\; \{(\; x\_\; \{2\}\; -x\_\; \{1\})\; ^\; \{2\}\; +\; (y\_\; \{2\}\; -y\_\; \{1\})\; ^\; \{2\}\; +\; (z\_\; \{2\}\; -z\_\; \{1\})\; ^\; \{2\}\}\}\}$

приводит к одному уравнению с одним неизвестным, в котором мы можем решить для z 2. Одно из x 1, x 2, y 1, y 2, z 1 или z 2 может быть неизвестным.

В отличие от классической теоремы о равнораспределении, при комнатной температуре колебательное движение молекул обычно вносит незначительный вклад в теплоемкость. Это происходит потому, что эти степени свободы заморожены, потому что расстояние между собственными значениями энергии превышает энергию, соответствующую окружающим температурам (kBT). В следующей таблице такие степени свободы не учитываются из-за их низкого влияния на общую энергию. Тогда только поступательная и вращательная степени свободы в равной степени вносят вклад в отношение теплоемкости. Вот почему γ = 5/3 для одноатомных газов и γ = 7/5 для двухатомных газов при комнатной температуре.

Однако при очень высоких температурах, порядка колебательной температуры (Θ vib), нельзя пренебрегать колебательным движением.

Колебательные температуры находятся в диапазоне от 10 K до 10 K.

	Одноатомные	Линейные молекулы	Нелинейные молекулы
Смещение (x, y и z)	3	3	3
Вращение (x, y и z)	0	2	3
Всего (без учета вибрации при комнатной температуре)	3	5	6
Вибрация	0	3N - 5	3N - 6
Всего (включая вибрацию)	3	3N	3N

Независимые степени свободы

Набор степеней свободы X 1,..., X N системы является независимым, если энергия, связанная с набор можно записать в следующей форме:

$E\; =\; \sum \; i\; =\; 1\; NE\; i\; (X\; i),\; \{\backslash \; displaystyle\; E\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; E\_\; \{i\}\; (X\_\; \{\; i\}),\}$

где E i - функция единственной переменной X i.

, пример: если X 1 и X 2 - два степеней свободы, а E - соответствующая энергия:

• Если $E\; =\; X\; 1\; 4\; +\; X\; 2\; 4\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{4\}\; +\; X\_\; \{2\}\; ^\; \{4\}\}$, то две степени свободы независимы.
• Если $E\; =\; X\; 1\; 4\; +\; X\; 1\; X\; 2\; +\; X\; 2\; 4\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{4\}\; +\; X\_\; \{1\}\; X\_\; \{2\}\; +\; X\_\; \{2\}\; ^\; \{4\}\}$, th Common crawl ru две степени свободы не независимы. Термин, включающий произведение X 1 и X 2, представляет собой термин связи, который описывает взаимодействие между двумя степенями свободы.

Для i от 1 до N значение i-й степени свободы X i распределяется согласно распределению Больцмана. Его функция плотности вероятности имеет следующий вид:

$pi\; (X\; i)\; =\; e\; -\; E\; ik\; BT\; \int \; d\; X\; ie\; -\; E\; ik\; BT\; \{\backslash \; displaystyle\; p\_\; \{i\}\; (X\_\; \{i\})\; =\; \{\backslash \; frac\; \{e\; ^\; \{-\; \{\backslash \; frac\; \{E\_\; \{i\}\}\; \{k\_\; \{B\}\; T\}\}\}\}\; \{\backslash \; int\; dX\_\; \{i\}\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{E\_\; \{i\}\}\; \{\; k\_\; \{B\}\; T\}\}\}\}\}\}$,

В этом разделе и по всей статье квадратные скобки $⟨⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; rangle\}$обозначают среднее значение количества, которое они включают.

внутренняя энергия системы представляет собой сумму средних энергий, связанных с каждой из степеней свободы:

$⟨E⟩\; =\; \sum \; i\; =\; 1\; N\; ⟨E\; i⟩.\; \{\backslash \; displaystyle\; \backslash \; langle\; E\; \backslash \; rangle\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; langle\; E\_\; \{i\}\; \backslash \; rangle.\}$

Квадратичные степени свободы

Степень свободы X i является квадратичным, если члены энергии, связанные с этой степенью свободы, могут быть записаны как

$E\; =\; \alpha \; i\; X\; i\; 2\; +\; \beta \; i\; X\; i\; Y\; \{\backslash \; displaystyle\; E\; =\; \backslash \; alpha\; \_\; \{i\}\; \backslash ,\; \backslash ,\; X\_\; \{i\}\; ^\; \{2\}\; +\; \backslash \; beta\; \_\; \{i\}\; \backslash ,\; \backslash ,\; X\_\; \{i\}\; Y\}$,

, где Y - линейная комбинация других квадратичных степеней свободы.

Пример: если X 1 и X 2 - две степени свободы, а E - соответствующая энергия:

• Если $E\; =\; X\; 1\; 4\; +\; Икс\; 1\; 3\; Икс\; 2\; +\; Икс\; 2\; 4\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{4\}\; +\; X\_\; \{1\}\; ^\; \{3\}\; X\_\; \{2\}\; +\; X\_\; \{2\}\; ^\; \{4\}\}$, то две степени свободы не являются независимыми и неквадратичными.
• Если $E\; =\; X\; 1\; 4\; +\; X\; 2\; 4\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{4\}\; +\; X\_\; \{2\}\; ^\; \{4\}\}$, то две степени свободы независимы и неквадратичны.
• Если $E\; =\; X\; 1\; 2\; +\; X\; 1\; X\; 2\; +\; 2\; X\; 2\; 2\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{2\}\; +\; X\_\; \{1\}\; X\_\; \{2\}\; +\; 2X\_\; \{2\}\; ^\; \{2\}\}$, тогда две степени свободы не являются независимыми, но квадратичными.
• Если $E\; =\; X\; 1\; 2\; +\; 2\; X\; 2\; 2\; \{\backslash \; displaystyle\; E\; =\; X\_\; \{1\}\; ^\; \{2\}\; +\; 2X\_\; \{2\}\; ^\; \{2\}\}$, тогда две степени свободы независимы и квадратичны.

Например, в механике Ньютона, динамика системы квадратичных степеней свободы управляются набором однородных линейных дифференциальных уравнений с постоянными коэффициентами.

Quadratic и i nзависимые степени свободы

X1,..., X N являются квадратичными и независимыми степенями свободы, если энергия, связанная с микросостоянием системы, которую они представляют, может быть записана как:

$E\; =\; \sum \; я\; знак\; равно\; 1\; N\; \alpha \; я\; Икс\; я\; 2\; \{\backslash \; displaystyle\; E\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; alpha\; \_\; \{i\}\; X\_\; \{i\}\; ^\; \{2\}\}$

Теорема о равнораспределении

В классическом пределе статистической механики, при термодинамическом равновесии, внутренняя энергия системы N квадратичных и независимых степеней свободы составляет:

$U\; =\; ⟨E⟩\; =\; N\; k\; BT\; 2\; \{\backslash \; displaystyle\; U\; =\; \backslash \; langle\; E\; \backslash \; rangle\; =\; N\; \backslash ,\; \{\backslash \; frac\; \{k\_\; \{B\}\; T\}\; \{2\}\}\}$

Здесь означает энергия, связанная со степенью свободы:

$⟨E\; i⟩\; =\; \int \; d\; X\; i\; \alpha \; i\; X\; i\; 2\; pi\; (X\; i)\; =\; \int \; d\; X\; i\; \alpha \; i\; X\; i\; 2\; e\; -\; \alpha \; i\; X\; i\; 2\; К\; BT\; \int \; d\; Икс\; ie\; -\; \alpha \; я\; Икс\; я\; 2\; К\; BT\; \{\backslash \; Displaystyle\; \backslash \; langle\; E\_\; \{i\}\; \backslash \; rangle\; =\; \backslash \; int\; dX\_\; \{i\}\; \backslash ,\; \backslash ,\; \backslash \; alpha\; \_\; \{i\}\; X\_\; \{i\}\; ^\; \{2\; \}\; \backslash ,\; \backslash ,\; p\_\; \{i\}\; (X\_\; \{i\})\; =\; \{\backslash \; frac\; \{\backslash \; int\; dX\_\; \{i\}\; \backslash ,\; \backslash ,\; \backslash \; alpha\; \_\; \{i\}\; X\_\; \{i\}\; ^\; \{2\}\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{\backslash \; alpha\; \_\; \{i\}\; X\_\; \{i\}\; ^\; \{2\}\}\; \{k\_\; \{B\}\; T\}\}\}\}\; \{\backslash \; int\; dX\_\; \{i\}\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{\; \backslash \; alpha\; \_\; \{i\}\; X\_\; \{i\}\; ^\; \{2\; \}\}\; \{k\_\; \{B\}\; T\}\}\}\}\}\}$

$⟨E\; i⟩\; =\; k\; BT\; 2\; \int \; dxx\; 2\; e\; -\; x\; 2\; 2\; \int \; dxe\; -\; x\; 2\; 2\; =\; k\; BT\; 2\; \{\backslash \; displaystyle\; \backslash \; langle\; E\_\; \{\; i\}\; \backslash \; rangle\; =\; \{\backslash \; frac\; \{k\_\; \{B\}\; T\}\; \{2\}\}\; \{\backslash \; frac\; \{\backslash \; int\; dx\; \backslash ,\; \backslash ,\; x\; ^\; \{2\}\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{x\; ^\; \{\; 2\}\}\; \{2\}\}\}\}\; \{\backslash \; int\; dx\; \backslash ,\; \backslash ,\; e\; ^\; \{-\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{2\}\}\}\}\}\; =\; \{\backslash \; frac\; \{k\_\; \{B\}\; T\}\; \{\; 2\}\}\}$

Поскольку степени свободы независимы, внутренняя энергия системы равна сумме средней энергии, связанной с каждой степенью свободы, которая демонстрирует результат.

Обобщения

Описание состояния системы как точки в ее фазовом пространстве, хотя и удобно с математической точки зрения, считается фундаментально неточным. В квантовой механике степени свободы движения заменены концепцией волновой функции, а операторы, которые соответствуют другим степеням свободы, имеют дискретные спектры. Например, оператор собственного углового момента (который соответствует свободе вращения) для электрона или фотона имеет только два собственных значения. Эта дискретность становится очевидной, когда действие имеет порядок постоянной Планка, и можно различать отдельные степени свободы.

Ссылки