Реакционно-диффузионная система

редактировать

Тип математической модели

Моделирование двух виртуальных химических веществ, реагирующих и распространяющихся на торусе, с использованием серого –Модель Скотта

Реакционно-диффузионные системы - это математические модели, которые соответствуют нескольким физическим явлениям. Наиболее распространенным является изменение концентрации одного или нескольких химических веществ в пространстве и времени: локальные химические реакции, в которых вещества превращаются друг в друга, и диффузия, вызывающая вещества для распределения по поверхности в космосе.

Реакционно-диффузионные системы естественно применяются в химии. Однако система также может описывать динамические процессы нехимической природы. Примеры можно найти в биологии, геологии и физике (теория диффузии нейтронов) и экологии. Математически системы реакция – диффузия имеют форму полулинейных параболических уравнений в частных производных. Их можно представить в общем виде

∂ tq = D _ _ ∇ 2 q + R (q), {\ displaystyle \ partial _ {t} {\ boldsymbol {q}} = {\ underline {\ underline { \ boldsymbol {D}}}} \, \ nabla ^ {2} {\ boldsymbol {q}} + {\ boldsymbol {R}} ({\ boldsymbol {q}}),}

\ partial _ {t} {\ boldsymbol {q}} = {\ underline {\ underline {\ bo ldsymbol {D}}}} \, \ nabla ^ {2} {\ boldsymbol {q}} + {\ boldsymbol {R}} ({\ boldsymbol {q}}),

где q(x, t) представляет неизвестную векторную функцию, D представляет собой диагональную матрицу из коэффициентов диффузии, а R учитывает все локальные реакции. Решения уравнений реакция-диффузия демонстрируют широкий диапазон поведения, включая образование бегущих волн и волновых явлений, а также других самоорганизующихся паттернов как полосы, шестиугольники или более сложные структуры, такие как диссипативные солитоны. Такие паттерны получили название «паттернов Тьюринга ». Каждая функция, для которой выполняется дифференциальное уравнение реакции диффузии, фактически представляет собой переменную концентрации.

Содержание

1 Однокомпонентные уравнения реакции-диффузии
2 Двухкомпонентные уравнения реакции-диффузии
3 Трехкомпонентные и более -компонентные уравнения реакции-диффузии
4 Применение и универсальность
5 Эксперименты
6 Численные методы
7 См. Также
8 Примеры
9 Ссылки
10 Внешние ссылки

Однокомпонентные уравнения реакции – диффузии

Простейшая реакция– уравнение диффузии находится в одном пространственном измерении в плоской геометрии,

∂ tu = D ∂ x 2 u + R (u), {\ displaystyle \ partial _ {t} u = D \ partial _ {x} ^ {2} u + R (u),}

\ partial _ {t} u = D \ partial _ {x} ^ {2} u + R (u),

также называется уравнением Колмогорова – Петровского – Пискунова. Если член реакции обращается в нуль, то уравнение представляет собой чистый процесс диффузии. Соответствующее уравнение - второй закон Фика. Выбор R (u) = u (1 - u) дает уравнение Фишера, которое первоначально использовалось для описания распространения биологических популяций, уравнение Ньюэлла-Уайтхеда-Сегеля с R ( u) = u (1 - u) для описания конвекции Рэлея – Бенара, более общего уравнения Зельдовича с R (u) = u (1 - u) (u - α) и 0 < α < 1 that arises in теория горения и ее частный вырожденный случай с R (u) = u - u, который иногда также называют уравнением Зельдовича.

Динамика однокомпонентных систем имеет определенные ограничения, так как уравнение эволюции также может быть записано в вариационной форме

∂ tu = - δ L δ u {\ displaystyle \ partial _ {t} u = - {\ frac {\ delta {\ mathfrak { L}}} {\ delta u}}}

\ partial _ {t} u = - {\ frac {\ delta {\ mathfrak {L}}} {\ delta u }}

и поэтому описывает постоянное уменьшение «свободной энергии» $L {\ displaystyle {\ mathfrak {L}}}$ ${\ mathfrak {L}}$ , заданное функционал

L = ∫ - ∞ ∞ [D 2 (∂ xu) 2 - V (u)] dx {\ displaystyle {\ mathfrak {L}} = \ int _ {- \ infty} ^ {\ infty} \ left [{\ tfrac {D} {2}} \ left (\ partial _ {x} u \ right) ^ {2} -V (u) \ right] \, {\ text {d}} x}

{\ displaystyle { \ mathfrak {L}} = \ int _ {- \ infty} ^ {\ infty} \ left [{\ tfrac {D} {2}} \ left (\ partial _ {x} u \ right) ^ {2} -V (u) \ right] \, {\ text {d}} x}

с потенциалом V (u) таким, что R (u) = dV (u) / du.

Фронт бегущей волны для уравнения Фишера.

В системах с более чем одним стационарным однородным решением типичное решение дается бегущими фронтами, соединяющими однородные состояния. Эти решения движутся с постоянной скоростью, не меняя своей формы, и имеют вид u (x, t) = û (ξ) с ξ = x - ct, где c - скорость бегущей волны. Обратите внимание, что хотя бегущие волны являются обычно стабильными структурами, все немонотонные стационарные решения (например, локализованные области, состоящие из пары фронт-антифронт) нестабильны. Для c = 0 есть простое доказательство этого утверждения: если u 0 (x) - стационарное решение и u = u 0 (x) + ũ (x, t) является бесконечно возмущенным решением, линейный анализ устойчивости дает уравнение

∂ tu ~ = D ∂ x 2 u ~ - U (x) u ~, U (x) = - R ′ (u) | и = и 0 (х). {\ displaystyle \ partial _ {t} {\ tilde {u}} = D \ partial _ {x} ^ {2} {\ tilde {u}} - U (x) {\ tilde {u}}, \ qquad U (x) = - R ^ {\ prime} (u) {\ Big |} _ {u = u_ {0} (x)}.}

{\ displaystyle \ partial _ {t} {\ tilde {u}} = D \ partial _ {x} ^ {2} { \ tilde {u}} - U (x) {\ tilde {u}}, \ qquad U (x) = - R ^ {\ prime} (u) {\ Big |} _ {u = u_ {0} ( х)}.}

С анзацем ũ = ψ (x) exp (−λt) мы приходим к задаче на собственные значения

H ^ ψ = λ ψ, H ^ = - D ∂ x 2 + U (x), {\ displaystyle {\ hat {H}} \ psi = \ lambda \ psi, \ qquad {\ hat {H}} = - D \ partial _ {x} ^ {2} + U (x),}

{\ hat {H}} \ psi = \ lambda \ psi, \ qquad {\ hat {H}} = - D \ partial _ {x} ^ {2} + U (x),

типа типа Шредингера, где отрицательные собственные значения приводят к неустойчивости решения. Из-за трансляционной инвариантности ψ = ∂ xu0(x) является нейтральной собственной функцией с собственным значением λ = 0, а все остальные собственные функции могут быть отсортированы по возрастающему числу узлов. с величиной соответствующего действительного собственного значения монотонно возрастает с увеличением числа нулей. Собственная функция ψ = ∂ xu0(x) должна иметь по крайней мере один нуль, а для немонотонного стационарного решения соответствующее собственное значение λ = 0 не может быть наименьшим, что подразумевает нестабильность.

Чтобы определить скорость c движущегося фронта, можно перейти в движущуюся систему координат и посмотреть на стационарные решения:

D ∂ ξ 2 u ^ (ξ) + c ∂ ξ u ^ (ξ) + Р (и ^ (ξ)) = 0. {\ Displaystyle D \ partial _ {\ xi} ^ {2} {\ hat {u}} (\ xi) + c \ partial _ {\ xi} {\ hat {u}} (\ xi) + R ({\ hat {u}} (\ xi)) = 0.}

D \ partial _ {\ xi} ^ {2} {\ hat {u}} (\ xi) + c \ partial _ {\ xi} {\ hat {u}} (\ xi) + R ({\ hat {u}} (\ xi)) = 0.

Это уравнение имеет хороший механический аналог как движение массы D с положением û в ход «времени» ξ под действием силы R с коэффициентом демпфирования c, который позволяет довольно наглядно получить доступ к построению различных типов решений и определению c.

При переходе от одного измерения пространства к нескольким, ряд утверждений из одномерных систем все еще может применяться. Плоские или изогнутые волновые фронты являются типичными структурами, и новый эффект возникает, когда локальная скорость изогнутого фронта становится зависимой от локального радиуса кривизны (это можно увидеть, перейдя к полярным координатам ). Это явление приводит к так называемой нестабильности, обусловленной кривизной.

Двухкомпонентные уравнения реакции-диффузии

Двухкомпонентные системы допускают гораздо больший диапазон возможных явлений, чем их однокомпонентные аналоги. Важная идея, которая была впервые предложена Аланом Тьюрингом, заключается в том, что состояние, которое стабильно в локальной системе, может стать нестабильным в присутствии диффузии.

Однако линейный анализ устойчивости показывает, что при линеаризации общая двухкомпонентная система

(∂ tu ∂ tv) = (D u 0 0 D v) (∂ xxu ∂ xxv) + (F (u, v) G (u, v)) {\ displaystyle {\ begin {pmatrix} \ partial _ {t} u \\\ partial _ {t} v \ end {pmatrix}} = {\ begin {pmatrix} D_ {u} 0 \\ 0 D_ {v} \ end {pmatrix}} {\ begin {pmatrix} \ partial _ {xx} u \\\ partial _ {xx} v \ end {pmatrix}} + {\ begin {pmatrix} F (u, v) \\ G (u, v) \ end {pmatrix}}}

{\ displaystyle {\ begin {pmatrix} \ partial _ {t} u \\\ partial _ {t} v \ конец {pmatrix}} = {\ begin {pmatrix} D_ {u} 0 \\ 0 D_ {v} \ end {pmatrix}} {\ begin {pmatrix} \ partial _ {xx} u \\\ partial _ {xx} v \ end {pmatrix}} + {\ begin {pmatrix} F (u, v) \\ G (u, v) \ end {pmatrix}}}

a плоская волна возмущение

q ~ k (x, t) = (u ~ (t) v ~ (t)) eik ⋅ x {\ displaystyle {\ tilde {\ boldsymbol {q}}} _ {\ boldsymbol {k}} ({\ boldsymbol {x}}, t) = {\ begin {pmatrix} {\ tilde {u}} (t) \\ {\ tilde {v} } (t) \ end {pmatrix}} e ^ {i {\ boldsymbol {k}} \ cdot {\ boldsymbol {x}}}}

{\ tilde {\ boldsym bol {q}}} _ {\ boldsymbol {k}} ({\ boldsymbol {x}}, t) = {\ begin {pmatrix} {\ tilde {u}} (t) \\ {\ tilde {v} } (t) \ end {pmatrix}} e ^ {i {\ boldsymbol {k}} \ cdot {\ boldsymbol {x}}}

стационарного однородного решения будет удовлетворять

(∂ tu ~ k (t) ∂ tv ~ k (t)) = - k 2 (D uu ~ k (t) D vv ~ k (t)) + R ′ (u ~ k (t) v ~ k (t)). {\ displaystyle {\ begin {pmatrix} \ partial _ {t} {\ tilde {u}} _ {\ boldsymbol {k}} (t) \\\ partial _ {t} {\ tilde {v}} _ { \ boldsymbol {k}} (t) \ end {pmatrix}} = - k ^ {2} {\ begin {pmatrix} D_ {u} {\ tilde {u}} _ {\ boldsymbol {k}} (t) \\ D_ {v} {\ tilde {v}} _ {\ boldsymbol {k}} (t) \ end {pmatrix}} + {\ boldsymbol {R}} ^ {\ prime} {\ begin {pmatrix} { \ tilde {u}} _ {\ boldsymbol {k}} (t) \\ {\ tilde {v}} _ {\ boldsymbol {k}} (t) \ end {pmatrix}}.}

{\ begin {pmatrix} \ partial _ {t} {\ tilde {u}} _ {\ boldsymbol {k}} (t) \\\ partial _ {t} {\ tilde {v}} _ {\ boldsymbol {k}} (t) \ end {pmatrix}} = - k ^ {2} {\ begin {pmatrix} D_ {u} {\ tilde {u}} _ {\ boldsymbol {k}} (t) \\ D_ {v} {\ tilde {v}} _ {\ boldsymbol {k}} (t) \ end {pmatrix}} + { \ boldsymbol {R}} ^ {\ prime} {\ begin {pmatrix} {\ tilde {u}} _ {\ boldsymbol {k}} (t) \\ {\ tilde {v}} _ {\ boldsymbol {k }} (t) \ end {pmatrix}}.

Идея Тьюринга могут быть реализованы только в четырех классах эквивалентности систем, характеризующихся знаками якобиана R′ функции реакции. В частности, если предполагается, что конечный волновой вектор k является наиболее неустойчивым, якобиан должен иметь знаки

(+ - + -), (+ + - -), (- + - +), (- - + +). {\ displaystyle {\ begin {pmatrix} + - \\ + - \ end {pmatrix}}, \ quad {\ begin {pmatrix} + + \\ - - \ end {pmatrix}}, \ quad { \ begin {pmatrix} - + \\ - + \ end {pmatrix}}, \ quad {\ begin {pmatrix} - - \\ + + \ end {pmatrix}}.}

{\ begin {pmatrix} + - \\ + - \ end {pmatrix}}, \ quad {\ begin {pmatrix} + + \\ - - \ end {pmatrix}}, \ quad {\ begin {pmatrix} - + \\ - + \ end {pmatrix}}, \ quad {\ begin {pmatrix} - - \\ + + \ end {pmatrix}}.

Этот класс Система названа системой активатор-ингибитор в честь ее первого представителя: близко к основному состоянию, один компонент стимулирует производство обоих компонентов, а другой ингибирует их рост. Его наиболее ярким представителем является уравнение ФитцХью – Нагумо

∂ tu = du 2 ∇ 2 u + f (u) - σ v, τ ∂ tv = dv 2 ∇ 2 v + u - v {\ displaystyle { \ begin {align} \ partial _ {t} u = d_ {u} ^ {2} \, \ nabla ^ {2} u + f (u) - \ sigma v, \\\ tau \ partial _ {t} v = d_ {v} ^ {2} \, \ nabla ^ {2} v + uv \ end {align}}}

{\ begin {align} \ partial _ {t} u = d_ {u} ^ {2} \, \ nabla ^ {2} u + f (u) - \ sigma v, \\\ tau \ partial _ {t} v = d_ {v} ^ {2} \, \ nabla ^ {2} v + uv \ end {align}}

с f (u) = λu - u - κ, который описывает, как действие потенциал проходит через нерв. Здесь d u, d v, τ, σ и λ - положительные константы.

Когда система активатор-ингибитор претерпевает изменение параметров, можно перейти от условий, при которых однородное основное состояние является стабильным, к условиям, при которых оно является линейно нестабильным. Соответствующая бифуркация может быть либо бифуркацией Хопфа в глобально колеблющееся однородное состояние с доминирующим волновым числом k = 0, либо бифуркацией Тьюринга в глобально структурированное состояние с доминирующим конечным волновым числом.. Последнее в двух пространственных измерениях обычно приводит к полосатым или шестиугольным узорам.

Подкритическая бифуркация Тьюринга: формирование гексагональной структуры из зашумленных начальных условий в вышеупомянутой двухкомпонентной системе реакция-диффузия типа Фитцхью-Нагумо.
Зашумленные начальные условия при t = 0.
Состояние системы при t = 10.
Почти сходящееся состояние при t = 100.

Для примера Фитцхью – Нагумо кривые нейтральной устойчивости, обозначающие границу линейно устойчивой области для бифуркаций Тьюринга и Хопфа, имеют вид

qn H (k): 1 τ + (du 2 + 1 τ dv 2) k 2 = f ′ (uh), qn T (k): κ 1 + dv 2 k 2 + du 2 k 2 = f ′ (uh). {\ displaystyle {\ begin {align} q _ {\ text {n}} ^ {H} (k): {} \ quad {\ frac {1} {\ tau}} + \ left (d_ {u} ^ {2} + {\ frac {1} {\ tau}} d_ {v} ^ {2} \ right) k ^ {2} = f ^ {\ prime} (u_ {h}), \\ [6pt ] q _ {\ text {n}} ^ {T} (k): {} \ quad {\ frac {\ kappa} {1 + d_ {v} ^ {2} k ^ {2}}} + d_ { u} ^ {2} k ^ {2} = f ^ {\ prime} (u_ {h}). \ end {align}}}

{\ begin {align} q _ {\ text {n}} ^ {H} (k): {} \ quad {\ frac {1 } {\ tau}} + \ left (d_ {u} ^ {2} + {\ frac {1} {\ tau}} d_ {v} ^ {2} \ right) k ^ {2} = f ^ {\ prime} (u_ {h}), \\ [6pt] q _ {\ text {n}} ^ {T} (k): {} \ quad {\ frac {\ kappa} {1 + d_ {v } ^ {2} k ^ {2}}} + d_ {u} ^ {2} k ^ {2} = f ^ {\ prime} (u_ {h}). \ End {align}}

Если бифуркация субкритическая, часто локализованные структуры (диссипативные солитоны ) можно наблюдать в гистерезисной области, где паттерн сосуществует с основным состоянием. Другие часто встречающиеся структуры включают последовательности импульсов (также известные как периодические бегущие волны ), спиральные волны и целевые узоры. Эти три типа решений также являются общими чертами двух (или более) компонентных уравнений реакции-диффузии, в которых локальная динамика имеет стабильный предельный цикл.

Другие закономерности, обнаруженные в вышеупомянутой двухкомпонентной системе реакции-диффузии Фитцхью– Тип нагумо.
Вращающаяся спираль.
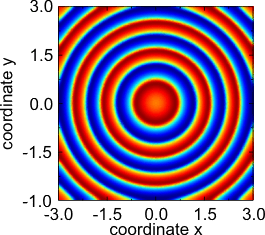
Целевой шаблон.
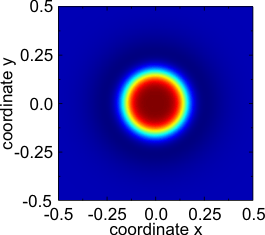
Стационарный локализованный импульс (диссипативный солитон).

Трех- и более-компонентные уравнения реакции-диффузии

Для различных систем были предложены уравнения реакции-диффузии с более чем двумя компонентами, например в качестве моделей для регуляции лимфангиогенеза с помощью VEGFC, MMP2 и коллагена I ; реакция Белоусова-Жаботинского, для систем свертывания крови или планарных газоразрядных систем.

Известно, что системы с большим количеством компонентов позволяют множество явлений, невозможных в системах с одним или двумя компонентами (например, стабильные бегущие импульсы в более чем одном пространственном измерении без глобальной обратной связи). Введение и систематический обзор возможных явлений в зависимости от свойств базовой системы даны в.

Проблемы, создаваемые многокомпонентными системами, коренятся в их аналитически трудноразрешимой природе; Одно из решений - исследовать параметрическое пространство такой модели по одной точке за раз, а затем решать модель численно, как это было сделано в теоретическом исследовании о лимфангиогенезе.

Применение и универсальность

В недавнем прошлом раз, системы реакции-диффузии привлекали большой интерес как прототип модели для формирования структуры. Вышеупомянутые паттерны (фронты, спирали, мишени, шестиугольники, полосы и диссипативные солитоны) можно найти в различных типах реакционно-диффузионных систем, несмотря на большие расхождения, например, в условиях местной реакции. Также утверждалось, что процессы реакции-диффузии являются важной основой процессов, связанных с морфогенезом в биологии, и могут даже быть связаны с шерстью животных и пигментацией кожи. Другие применения уравнений реакции-диффузии включают экологические вторжения, распространение эпидемий, рост опухолей и заживление ран. Еще одна причина интереса к реакционно-диффузионным системам заключается в том, что, хотя они и являются нелинейными уравнениями в частных производных, часто есть возможности для их аналитической обработки.

Эксперименты

Хорошо контролируемые эксперименты по химической реакции– До настоящего времени диффузионные системы реализовывались тремя способами. Во-первых, можно использовать гелевые реакторы или заполненные капиллярные трубки. Во-вторых, были исследованы импульсы температуры на каталитических поверхностях. В-третьих, распространение бегущих нервных импульсов моделируется с помощью систем реакции-диффузии.

Помимо этих общих примеров, оказалось, что при определенных обстоятельствах системы электрического транспорта, такие как плазма или полупроводники, могут быть описаны в реакции– диффузионный подход. Для этих систем были проведены различные эксперименты по формированию рисунка.

Численные методы

Реакционно-диффузионная система может быть решена с использованием методов вычислительной математики. В исследовательской литературе существует несколько числовых методов лечения. Также для сложных геометрий предлагаются численные методы решения.

См. Также

Примеры

Ссылки

Внешние ссылки

Реакция – диффузия по модели Грея – Скотта: параметризация Пирсона визуальная карта пространство параметров диффузии по реакции Грея – Скотта.
Диссертация о реакционно-диффузионных моделях с обзором поля