Распределительная решетка

В математике распределительная решетка представляет собой решетку в котором операции соединяются и встречаются распределяют друг над другом. Типичными примерами таких структур являются наборы множеств, для которых операции решетки могут быть заданы множеством union и пересечением. В самом деле, эти решетки множеств полностью описывают декорацию: каждая дистрибутивная решетка - с точностью до изоморфизма - задана как такая решетка множеств.

• 1 Определение
• 2 Морфизмы
• 3 Примеры
• 4 Характеристические свойства
• 5 Теория представлений
• 6 Свободные распределительные решетки
• 7 См. Также
• 8 Ссылки
• 9 Дополнительная литература

Как и в случае произвольных решеток, можно выбрать рассмотрение дистрибутивной решетки L либо как структуру теории порядка, либо универсальная алгебра. Оба взгляда и их взаимное соответствие обсуждаются в статье о решетках. В данной ситуации алгебраическое описание кажется более удобным:

Решетка (L, ∨, ∧) дистрибутивна, если следующее дополнительное тождество выполняется для всех x, y и z в L:

x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z).

Если рассматривать решетки как частично упорядоченные множества, это означает, что операция встречи сохраняет непустые конечные соединения. Основным фактом теории решеток является то, что указанное выше условие эквивалентно его двойственному :

x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) для всех x, y и z в L.

В каждой решетке, определяя p≤q, как обычно, означающим p∧q = p, выполняется неравенство x ∧ (y ∨ z) ≥ (x ∧ y) ∨ (x ∧ z), а также его двойственное неравенство x ∨ (y ∧ z) ≤ (x ∨ y) ∧ (x ∨ z). Решетка дистрибутивна, если выполняется одно из обратных неравенств. Более подробную информацию о связи этого условия с другими условиями дистрибутивности теории порядка можно найти в статье о дистрибутивности (теории порядка).

Морфизм дистрибутивных решеток - это просто решеточный гомоморфизм. как указано в статье о решетках, то есть функции, которая совместима с двумя операциями решетки. Поскольку такой морфизм решеток сохраняет структуру решетки, следовательно, он также сохранит дистрибутивность (и, таким образом, будет морфизмом дистрибутивных решеток).

Решетка Юнга

Распределительные решетки встречаются повсеместно, но также имеют довольно специфические структуры. Как уже упоминалось, основным примером дистрибутивных решеток являются решетки множеств, где соединения и встречи задаются обычными теоретико-множественными операциями. Дополнительные примеры включают:

• Алгебра Линденбаума большинства логик, поддерживающих конъюнкцию и дизъюнкцию, является распределительной решеткой, т. Е. "И "распределяет по" или "и наоборот.
• Каждая логическая алгебра является распределительной решеткой.
• Каждая алгебра Гейтинга является распределительной решеткой. В особенности это включает все локали и, следовательно, все открытые множества решетки топологических пространств. Также обратите внимание, что алгебры Гейтинга можно рассматривать как алгебры Линденбаума интуиционистской логики, что делает их частным случаем первого примера.
• Каждое полностью упорядоченное множество является распределительная решетка с max в качестве соединения и min в качестве соответствия.
• натуральные числа образуют (условно полную) распределительную решетку, принимая наибольший общий делитель в качестве соответствия, а наименьшее общее кратное как объединение. Эта решетка также имеет наименьший элемент, а именно 1, который, следовательно, служит элементом идентичности для объединений.
• Если задано положительное целое число n, набор всех положительных делителей числа n образует дистрибутивный решетка, опять же с наибольшим общим делителем как meet и наименьшим общим кратным как join. Это булева алгебра тогда и только тогда, когда n бесквадратное.
• A упорядоченное по решетке векторное пространство является дистрибутивной решеткой.
• Решетка Юнга задана порядком включения Диаграммы Юнга, представляющие целочисленные разбиения, являются дистрибутивной решеткой.
• Точки дистрибутивного многогранника (выпуклый многогранник, замкнутый относительно координатно минимальные и покоординатные максимальные операции), причем эти две операции являются операциями соединения и пересечения решетки.

В начале развития теории решеток Чарльз С. Пирс считал, что все решетки дистрибутивны, что is, дистрибутивность следует из остальных аксиом решетки. Однако доказательства независимости были предоставлены Шредером, Фойгтом, Люротом, Корсельтом и Дедекиндом.

Различными существуют эквивалентные формулировки для приведенного выше определения. Например, L является дистрибутивным тогда и только тогда, когда для всех элементов x, y, z в L выполняется следующее:

(x$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$y)$\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$(y$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$z)$\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$(z$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$x) = (x $\vee \; \{\backslash \; displaystyle\; \backslash \; vee\; \}$y)$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$(y$\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$z)$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$(z$\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$x).

Аналогично, L является дистрибутивным тогда и только тогда, когда

x$\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$z = y $\wedge \; \{\backslash \; displaystyle\; \backslash \; wedge\}$z and x $\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$z = y $\vee \; \{\backslash \; displaystyle\; \backslash \; vee\}$z всегда подразумевает x = y.

• диаграммы Хассе из двух прототипов нераспределительных решеток
• 

  Алмазная решетка M 3 недистрибутивна: x ∧ (y ∨ z) = x ∧ 1 = x ≠ 0 = 0 ∨ 0 = (x ∧ у) ∨ (х ∧ г).

• 

  Решетка пятиугольника N 5 недистрибутивна: x ∧ (y ∨ z) = x ∧ 1 = x ≠ z = 0 ∨ z = (x ∧ y) ∨ (x ∧ z).

Распределительная решетка, которая содержит N5 (сплошные линии, слева) и M3 (справа) как подмножество, но не как подрешетка

Простейшими недистрибутивными решетками являются M 3, «алмазная решетка» и N 5, «пятиугольная решетка». Решетка дистрибутивна тогда и только тогда, когда ни одна из ее подрешеток не изоморфна M 3 или N 5 ; подрешетка - это подмножество, которое замкнуто относительно операций пересечения и соединения исходной решетки. Обратите внимание, что это не то же самое, что подмножество, представляющее собой решетку в исходном порядке (но, возможно, с другими операциями соединения и встречи). Дальнейшие характеристики выводятся из теории представлений в следующем разделе.

Наконец, распределенность влечет за собой несколько других приятных свойств. Например, элемент дистрибутивной решетки является meet-prime тогда и только тогда, когда он является meet-неприводимым, хотя последнее в общем случае является более слабым свойством. По двойственности то же самое верно для элементов join-prime и join-non-join. Если решетка является дистрибутивной, ее отношение покрытия образует медианный граф.

Кроме того, каждая распределительная решетка также модульная.

Введение уже намекнул на наиболее важную характеристику дистрибутивных решеток: решетка дистрибутивна тогда и только тогда, когда она изоморфна решетке множеств (замкнутой под объединением множеств и пересечением ). То, что объединение множеств и пересечение действительно являются дистрибутивными в указанном выше смысле, является элементарным фактом. Другое направление менее тривиально, поскольку требует изложенных ниже теорем представления. Важный вывод из этой характеристики состоит в том, что тождества (уравнения), которые выполняются во всех дистрибутивных решетках, являются в точности теми, которые выполняются во всех решетках множеств в указанном выше смысле.

Теорема Биркгофа о представлении для дистрибутивных решеток утверждает, что каждая конечная дистрибутивная решетка изоморфна решетке нижних множеств poset его простого соединения (эквивалентно: join -неприводимые) элементы. Это устанавливает биекцию (до изоморфизма ) между классом всех конечных множеств и классом всех конечных дистрибутивных решеток. Эта биекция может быть расширена до двойственности категорий между гомоморфизмами конечных дистрибутивных решеток и монотонными функциями конечных множеств. Однако обобщение этого результата на бесконечные решетки требует добавления дополнительной структуры.

Еще одна ранняя теорема о представлении теперь известна как теорема Стоуна о представлении для распределительных решеток (имя дано в честь Маршалла Харви Стоуна, который первым доказал ее). Он характеризует дистрибутивные решетки как решетки компактных открытых множеств некоторых топологических пространств. Этот результат можно рассматривать и как обобщение знаменитой теоремы Стоуна о представлении для булевых алгебр и как конкретизацию общих условий двойственности Стоуна.

. Еще одно важное представление было установлено Хилари Пристли в своей теореме представления для дистрибутивных решеток. В этой формулировке дистрибутивная решетка используется для построения топологического пространства с дополнительным частичным порядком в его точках, в результате чего получается упорядоченное (полностью разделенное порядком) каменное пространство (или пространство Пристли ). Исходная решетка восстанавливается как набор clopen нижних множеств этого пространства.

Как следствие теорем Стоуна и Пристли, легко видеть, что любая дистрибутивная решетка действительно изоморфна решетке множеств. Однако для доказательства обоих утверждений требуется теорема о булевом простом идеале, слабая форма выбранной аксиомы .

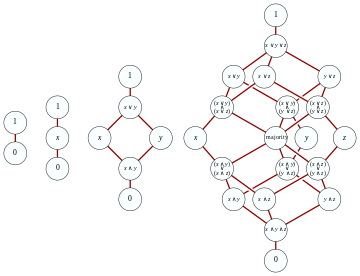Свободные дистрибутивные решетки на нуле, единице, два, и три генератора. Элементы с метками «0» и «1» представляют собой пустое соединение и пересечение, а элемент с меткой «большинство» равен (x ∧ y) ∨ (x ∧ z) ∨ (y ∧ z) = (x ∨ y) ∧ ( x ∨ z) ∧ (y ∨ z).

свободную дистрибутивную решетку над набором образующих G можно построить намного проще, чем общую свободную решетку. Первое наблюдение заключается в том, что, используя законы распределенности, каждый член, образованный бинарными операциями $\vee \; \{\backslash \; displaystyle\; \backslash \; lor\}$и $\wedge \; \{\backslash \; displaystyle\; \backslash \; land\}$на множестве образующих может быть преобразовано в следующую эквивалентную нормальную форму:

$M\; 1\; \vee \; M\; 2\; \vee \; \cdots \; \vee \; M\; n,\; \{\backslash \; displaystyle\; M\_\; \{1\}\; \backslash \; lor\; M\_\; \{2\}\; \backslash \; lor\; \backslash \; cdots\; \backslash \; lor\; M\_\; \{n\},\}$

где $M\; i\; \{\backslash \; displaystyle\; M\_\; \{i\}\}$- конечные пересечения элементов G. Более того, поскольку и встреча, и соединение являются ассоциативными, коммутативный и идемпотент, можно игнорировать дубликаты и порядок, и представлять соединение встреч, подобное приведенному выше, как набор наборов:

$\{N\; 1,\; N\; 2,\dots ,\; N\; n\},\; \{\backslash \; displaystyle\; \backslash \; \{N\_\; \{1\},\; N\_\; \{2\},\; \backslash \; ldots,\; N\_\; \{n\}\; \backslash \},\}$

где $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\; \}\}$- конечные подмножества G. Однако все еще возможно, что два таких члена обозначают один и тот же элемент дистрибутивной решетки. Это происходит, когда есть индексы j и k, такие что $N\; j\; \{\backslash \; displaystyle\; N\_\; \{j\}\}$является подмножеством $N\; k.\; \{\backslash \; displaystyle\; N\_\; \{k\}.\}$В этом случае пересечение $N\; k\; \{\backslash \; displaystyle\; N\_\; \{k\}\}$будет ниже пересечения $N\; j,\; \{\backslash \; displaystyle\; N\_\; \{j\},\}$и, следовательно, можно безопасно удалить избыточный набор $N\; k\; \{\backslash \; displaystyle\; N\_\; \{k\}\}$без изменения интерпретации весь срок. Следовательно, набор конечных подмножеств G будет называться неизбыточным, если все его элементы $N\; i\; \{\backslash \; displaystyle\; N\_\; \{i\}\}$взаимно несовместимы (относительно упорядочения подмножеств); то есть, когда он образует антицепь конечных множеств.

Теперь свободная дистрибутивная решетка над множеством образующих G определена на множестве всех конечных неизбыточных множеств конечных подмножеств G. Соединение двух конечных неизбыточных множеств наборы получается из их объединения путем удаления всех лишних наборов. Точно так же встреча двух множеств S и T является неизбыточной версией $\{N\; \cup \; M\; \mid \; N\; \in \; S,\; M\; \in \; T\}.\; \{\backslash \; displaystyle\; \backslash \; \{N\; \backslash \; cup\; M\; \backslash \; mid\; N\; \backslash \; in\; S,\; M\; \backslash \; in\; T\; \backslash \}.\}$Подтверждение того, что эта структура является распределительной решеткой с требуемым универсальным свойством это рутина.

Количество элементов в свободных распределительных решетках с n образующими задается числами Дедекинда. Эти числа быстро растут и известны только для n ≤ 8; это

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 (последовательность A000372 в OEIS ).

Числа выше подсчитывают количество элементов в свободном дистрибутивные решетки, в которых операции решетки являются соединениями и встречами конечных наборов элементов, включая пустое множество. Если пустые соединения и пустые встречи запрещены, в результирующих свободных распределительных решетках будет на два элемента меньше; их количество элементов формирует последовательность

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786 (последовательность A007153 в OEIS ).

• Полностью распределительная решетка - решетка в которой бесконечные объединения распределяются по бесконечности, соответствует
• теории двойственности для распределительных решеток
• Спектральное пространство

• Burris, Stanley N.; Sankappanavar, HP (1981). Курс универсальной алгебры. Springer-Verlag. ISBN 3-540-90578-2.