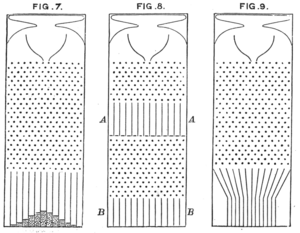
 Экспериментальная установка Гальтона ( Рис.8)
Экспериментальная установка Гальтона ( Рис.8) В статистике, регрессия к среднему (или регрессия к среднему ) - это явление, которое возникает, если образец точка случайной величины является экстремальной (почти выбросом ), будущая точка будет ближе к среднему или среднее по дальнейшим измерениям. Чтобы избежать неправильных выводов, при разработке научных экспериментов и интерпретации данных необходимо учитывать регрессию к среднему значению. Исторически то, что сейчас называется регрессией к среднему значению, также называлось возвращением к среднему и возвратом к среднему .
Условия, при которых происходит регрессия к среднему значению, зависят от того, как этот термин выражается математически. определены. Британский энциклопедист сэр Фрэнсис Гальтон впервые наблюдал это явление в контексте простой линейной регрессии точек данных. Гальтон разработал следующую модель: гранулы падают через quincunx, образуя нормальное распределение с центром непосредственно под их точкой входа. Эти гранулы затем могут быть выпущены во вторую галерею, соответствующую второму измерению. Затем Гальтон задал обратный вопрос: «Откуда взялись эти гранулы?»
Ответ был не «в среднем прямо выше». Скорее он был «в среднем ближе к середине» по той простой причине, что над ним, ближе к середине, было больше гранул, которые могли блуждать влево, чем их было в левом крайнем положении, которые могли блуждать вправо, внутрь.
Поскольку это менее ограничительный подход, регрессия к среднему значению может быть определена для любого двумерного распределения с идентичными маргинальными распределениями. Существует два таких определения. Одно определение полностью согласуется с обычным использованием термина «регрессия к среднему». Не все такие двумерные распределения показывают регресс к среднему значению в соответствии с этим определением. Однако все такие двумерные распределения демонстрируют регрессию к среднему значению при другом определении.
Джереми Сигел использует термин «возврат к среднему значению» для описания финансового временного ряда, в котором «доходность может быть очень нестабильной в краткосрочной перспективе, но очень стабильной. в долгосрочной перспективе." С количественной точки зрения, это тот, в котором стандартное отклонение средней годовой доходности уменьшается быстрее, чем величина, обратная величине периода удержания, подразумевая, что процесс не является случайным блужданием, а периоды за более низкой доходностью систематически следуют компенсирующие периоды более высокой доходности, как, например, в случае многих сезонных предприятий.
Рассмотрим простой пример: класс студентов берет тест "верно / неверно" из 100 пунктов по предмету. Предположим, что все студенты выбирают случайным образом по всем вопросам. Тогда оценка каждого студента будет реализацией одной из набора независимых и одинаково распределенных случайных величин с ожидаемым средним, равным 50. Естественно, некоторые просто случайно студенты наберут значительно больше 50, а некоторые значительно ниже 50. Если выбрать только 10% учащихся, набравших наибольшее количество баллов, и дать им второй тест, на котором они снова будут случайным образом выбирать все элементы, ожидается, что средний балл снова будет близок к 50. Таким образом, среднее значение этих учащихся будет "регрессировать". "вплоть до среднего значения всех студентов, сдавших первоначальный тест. Независимо от того, какой балл студент набрал в исходном тесте, лучший прогноз для его результата во втором тесте - 50.
Если выбор ответов на вопросы теста не был случайным, то есть если не повезло (хорошо или хорошо). плохо) или случайное угадывание, связанное с ответами, предоставленными учащимися - тогда ожидается, что все учащиеся наберут во втором тесте те же оценки, что и в исходном тесте, и не будет никакого регресса к среднему значению.
Наиболее реалистичные ситуации находятся между этими двумя крайностями: например, можно рассматривать результаты экзаменов как комбинацию навыка и удачи. В этом случае подмножество студентов, набравших больше среднего, будет состоять из тех, кто был квалифицирован и не особо повезло, а также из неквалифицированных, но чрезвычайно удачливых. При повторном тестировании этого подмножества неквалифицированный вряд ли повторит свой счастливый случай, в то время как у опытного будет второй шанс неудачника. Следовательно, те, кто хорошо справлялся ранее, вряд ли справятся так же хорошо во втором тесте, даже если оригинал не может быть воспроизведен.
Ниже приводится пример второго типа регрессии к среднему значению. Класс учеников сдает два выпуска одного и того же теста в течение двух дней подряд. Часто наблюдается, что худшие исполнители в первый день будут улучшать свои результаты во второй день, а лучшие исполнители в первый день будут иметь худшие результаты во второй день. Это явление возникает из-за того, что оценки учащихся частично определяются их способностями, а частично - случайностью. В первом тесте некоторым повезет, и они наберут больше, чем их способности, а некоторым не повезет и они наберут меньше, чем их способности. Некоторым удачливым ученикам на первом тесте снова повезет и на втором, но у многих из них будет (для них) средний балл или ниже среднего. Следовательно, ученик, которому повезло и который превзошел свои способности в первом тесте, с большей вероятностью получит худший результат во втором тесте, чем лучший результат. Точно так же учащиеся, которые, к несчастью, набрали меньше, чем их способности в первом тесте, будут иметь тенденцию к увеличению своих оценок во втором тесте. Чем больше влияние удачи на создание экстремального события, тем меньше вероятность того, что удача повторится в нескольких событиях.
Если ваша любимая спортивная команда выиграла чемпионат в прошлом году, что это означает для их шансов на победу в следующем сезоне? В той степени, в которой этот результат обусловлен мастерством (команда в хорошем состоянии, с лучшим тренером и т. Д.), Их победа сигнализирует о том, что в следующем году они с большей вероятностью выиграют снова. Но чем в большей степени это связано с удачей (другие команды оказались втянутыми в скандал с наркотиками, удачная ничья, выбор драфта оказался продуктивным и т. Д.), Тем меньше вероятность того, что они снова выиграют в следующем году.
Если одно медицинское исследование предполагает, что определенное лекарство или лечение превосходит все другие методы лечения какого-либо состояния, то во втором исследовании более вероятно, что эффективность этого препарата или лечения будет ближе к среднему значению в следующем квартале.
Если бизнес-организация имеет высокорентабельный квартал, несмотря на основные причины, по которым ее результаты остаются неизменными, она, скорее всего, будет хуже в следующем квартале.
Бейсболисты, которые хорошо сыграли сезон новичков, вероятно, будет хуже, чем второй; "Второкурсник ". Точно так же регресс к среднему значению является объяснением обложки Sports Illustrated jinx - периоды исключительной производительности, которые приводят к появлению функции обложки, вероятно, будут сменяться периодами более посредственной производительности, создавая впечатление, что появление на обложка вызывает у спортсмена упадок.
Концепция регрессии происходит от генетики и была популяризирована сэром Фрэнсисом Гальтоном в конце 19-го века. века с публикацией «Регресс к посредственности в наследственном росте». Гальтон заметил, что экстремальные характеристики (например, рост) родителей не передаются полностью их потомству. Скорее, характеристики потомства регрессируют к средней точке (точке, которая с тех пор была идентифицирована как среднее значение). Измеряя рост сотен людей, он смог количественно оценить регрессию к среднему и оценить размер эффекта. Гальтон писал, что «средняя регрессия потомства является постоянной долей их соответствующих отклонений от среднего уровня родителей ». Это означает, что различие между ребенком и его родителями по некоторым характеристикам пропорционально отклонению его родителей от типичных людей в популяции. Если каждый из его родителей на два дюйма выше, чем в среднем для мужчин и женщин, то, в среднем, потомок будет короче своих родителей в некоторый коэффициент (который сегодня мы бы назвали единицей минус коэффициент регрессии ) умножить на два дюйма. Что касается роста, Гальтон оценил этот коэффициент примерно как 2/3: рост человека будет измеряться примерно в средней точке, которая составляет две трети отклонения родителей от среднего показателя по популяции.
Гальтон ввел термин «регрессия» для описания наблюдаемого факта наследования многофакторных количественных генетических признаков: а именно, что потомство родителей, которые лежат в хвосте распределения, будет имеют тенденцию лежать ближе к центру, среднему значению распределения. Он количественно оценил эту тенденцию и при этом изобрел линейный регрессионный анализ, тем самым заложив основу для большей части современного статистического моделирования. С тех пор термин «регрессия» приобрел множество значений, и современные статистики могут использовать его для описания феномена систематической ошибки выборки, которая имеет мало общего с первоначальными наблюдениями Гальтона в области генетики..
Хотя его математический анализ был верен, биологическое объяснение Гальтоном феномена регрессии, которое он наблюдал, теперь, как известно, неверно. Он заявил: «Ребенок наследует частично от своих родителей, частично от своих предков. В целом, чем дальше уходит его генеалогия, тем многочисленнее и разнообразнее будет его родословная, пока они не перестанут отличаться от любой столь же многочисленной выборки, взятой наугад. от гонки в целом ". Это неверно, так как ребенок получает свой генетический состав исключительно от родителей. В генетическом материале нет пропуска поколений: любой генетический материал от более ранних предков должен был пройти через родителей (хотя он, возможно, не был выражен в них). Этот феномен станет лучше понят, если мы предположим, что наследственный признак (например, рост) контролируется большим количеством рецессивных генов. Исключительно высокие люди должны быть гомозиготными для мутаций увеличенного роста в большой части этих локусов. Но локусы, несущие эти мутации, не обязательно являются общими для двух высоких особей, и если эти особи спариваются, их потомство будет в среднем гомозиготным по «высоким» мутациям по меньшему количеству локусов, чем любой из их родителей. Кроме того, рост не полностью генетически обусловлен, но также подвержен влиянию окружающей среды во время развития, что делает потомство исключительных родителей еще более близким к среднему, чем их родители.
Этот популяционно-генетический феномен регрессии к среднему лучше всего рассматривать как комбинацию биномиально распределенного процесса наследования плюс нормально распределенные воздействия окружающей среды. Напротив, термин «регрессия к среднему» сейчас часто используется для описания явления, при котором первоначальная смещение выборки может исчезнуть, поскольку новые, повторяющиеся или более крупные выборки отображают выборочные средства, которые ближе к истинному базовое среднее значение населения.
Регрессия к среднему значению является важным фактором при дизайне экспериментов.
Возьмем гипотетический пример из 1000 человек того же возраста, которые были обследованы и получили оценку риск сердечного приступа. Статистические данные можно использовать для измерения успеха вмешательства среди 50 человек, относящихся к группе наибольшего риска. Вмешательство может заключаться в изменении диеты, физических упражнений или медикаментозном лечении. Даже если вмешательства бесполезны, можно ожидать, что тестовая группа покажет улучшение при следующем физическом осмотре из-за регресса к среднему значению. Лучшим способом борьбы с этим эффектом является случайное разделение группы на группу лечения, которая получает лечение, и группу контрольную, не получающую лечение. Тогда лечение будет считаться эффективным только в том случае, если в группе лечения улучшится больше, чем в контрольной группе.
В качестве альтернативы, группа неблагополучных детей может быть протестирована для выявления детей с наибольшим потенциалом колледжа. Можно было определить 1% лучших, и им были предоставлены специальные курсы повышения квалификации, репетиторство, консультации и компьютеры. Даже если программа эффективна, их средние баллы могут быть меньше, когда тест будет повторен через год. Однако в этих обстоятельствах может считаться неэтичным иметь контрольную группу детей из неблагополучных семей, чьи особые потребности игнорируются. Математический расчет для усадки может учесть этот эффект, хотя он не будет таким надежным, как метод контрольной группы (см. Также пример Стейна ).
Эффект также можно использовать для общего вывода и оценки. Сегодня в самом жарком месте страны завтра скорее будет прохладнее, чем жарче, чем сегодня. Наиболее эффективный паевой инвестиционный фонд за последние три года, скорее всего, испытает относительное снижение производительности, чем улучшение в течение следующих трех лет. Самый успешный голливудский актер этого года, скорее всего, получит меньше, чем больше, для своего следующего фильма. Бейсболист с самым высоким средним показателем к перерыву на Матч звезд, скорее всего, будет иметь более низкий средний показатель, чем более высокий средний показатель во второй половине сезона.
Концепция регресса к среднему значению может быть очень легко использована неправильно.
В приведенном выше примере теста студента неявно предполагалось, что измеряемое значение не изменилось между двумя измерениями. Предположим, однако, что курс был пройден / не пройден, и студенты должны были набрать более 70 баллов по обоим тестам, чтобы пройти. Тогда студенты, набравшие меньше 70 баллов в первый раз, не будут иметь стимула преуспевать и могут получить в среднем хуже во второй раз. С другой стороны, у студентов чуть старше 70 будет сильный стимул учиться и концентрироваться во время прохождения теста. В этом случае можно увидеть движение от 70, баллы ниже него становятся ниже, а баллы выше - выше. Изменения между временами измерения могут увеличивать, компенсировать или обращать статистическую тенденцию к регрессу к среднему значению.
Статистическая регрессия к среднему не является причинным явлением. Учащийся, набравший наихудшие баллы по тесту в первый день, не обязательно значительно повысит свой балл во второй день из-за эффекта. В среднем, худшие бомбардиры улучшаются, но это правда только потому, что худшие, скорее всего, были неудачниками, чем удачливыми. В той степени, в которой оценка определяется случайным образом или если оценка имеет случайные вариации или ошибки, в отличие от того, чтобы определяться академическими способностями учащегося или быть «истинной ценностью», явление будет иметь эффект. Классическая ошибка в этом плане была в образовании. Было замечено, что ученики, получившие похвалу за хорошую работу, показали более низкие результаты по следующему критерию, а ученики, которых наказали за плохую работу, показали, что они лучше справились со следующим критерием. Педагоги решили перестать хвалить и продолжать наказывать на этом основании. Такое решение было ошибкой, потому что регресс к среднему значению основан не на причине и следствии, а на случайной ошибке в естественном распределении вокруг среднего.
Хотя экстремальные индивидуальные измерения регрессируют к среднему, второй образец измерений будет не ближе к среднему, чем первый. Снова рассмотрим студентов. Предположим, что у экстремальных людей есть тенденция к регрессу на 10% пути к среднему 80, поэтому студент, набравший 100 в первый день, ожидал набрать 98 во второй день, а ученик, набравший 70 баллов в первый день, должен набрать 71 балл во второй день. Эти ожидания ближе к среднему, чем результаты первого дня. Но результаты второго дня будут отличаться от их ожиданий; некоторые будут выше, некоторые - ниже. Кроме того, людям, которые измеряют очень близко к среднему, следует ожидать отклонения от среднего. Эффект прямо противоположен регрессии к среднему значению и полностью компенсирует его. Таким образом, для экстремальных людей мы ожидаем, что вторая оценка будет ближе к среднему, чем первая оценка, но для всех людей мы ожидаем, что распределение расстояний от среднего будет одинаковым для обоих наборов измерений.
В связи с вышеизложенным, регрессия к среднему значению одинаково хорошо работает в обоих направлениях. Мы ожидаем, что учащийся, набравший наибольшее количество баллов во второй день, в первый день будет хуже. И если мы сравним лучшего ученика в первый день с лучшим учеником во второй день, независимо от того, тот же человек это или нет, есть тенденция к регрессу к среднему значению в любом направлении. Мы ожидаем, что лучшие результаты в оба дня будут одинаково далеки от среднего.
Многие явления, как правило, объясняются неправильными причинами, когда не учитывается регрессия к среднему.
Ярким примером является книга Горация Секриста «Триумф посредственности в бизнесе» 1933 года, в которой профессор статистики собрал огромное количество данных, чтобы доказать, что нормы прибыли конкурентоспособных предприятий имеют тенденцию к снижению. среднее с течением времени. На самом деле такого эффекта нет; изменчивость нормы прибыли практически постоянна во времени. Secrist описал только обычную регрессию к среднему значению. Один раздраженный рецензент, Гарольд Хотеллинг, сравнил книгу с «доказательством таблицы умножения, расположив слонов в ряды и столбцы, а затем проделав то же самое с множеством других видов животных».
расчет и интерпретация «баллов улучшения» по стандартизированным образовательным тестам в Массачусетсе, вероятно, являются еще одним примером ошибки регрессии. В 1999 году перед школами были поставлены цели улучшения. Для каждой школы Департамент образования свел в таблицу разницу в средних баллах, полученных учащимися в 1999 и 2000 годах. Было быстро отмечено, что большинство школ с наихудшими результатами достигли своих целей, что Министерство образования приняло за подтверждение. обоснованность их политики. Однако было также отмечено, что многие из якобы лучших школ Содружества, такие как Средняя школа Бруклина (с 18 финалистами Национальной стипендии), были объявлены провалившимися. Как и во многих случаях, связанных со статистикой и государственной политикой, этот вопрос обсуждается, но в последующие годы «оценки улучшений» не объявлялись, ирезультаты представляются случаем возврата к среднему значению.
Психолог Дэниел Канеман, предоставить Нобелевской программы по экономическим наукам 2002 года, указ, что возвращение к среднему значению может объяснить, почему упреки могут улучшить производительность, в то время как похвала, кажется, имеет неприятные последствия.
У меня был самый приятный опыт Eureka в моей карьере, когда я пытался научить летных инструкторов тому, что похвала более эффективна, чем наказание, за поощрение обучения навыкам. Когда я закончил свою восторженную речь, один из самых опытных преподавателей в аудитории инструктаж и произнес свою короткую речь, что положительное подкрепление может быть полезно для птиц, но продолжал отрицать, что это оптимально. для летных курсантов. Он сказал: «Во многих случаях я хвалил курсантов за чистое выполнение некоторых фигур высшего пилотажа, и в целом, когда они пробуют его снова, они делают хуже. С другой стороны, я часто кричал на курсантов за плохое выполнение и в общем, в следующий раз они добьются большего успеха. Поэтому, пожалуйста, не говорите нам, что подкрепление работает, а наказание - нет, потому что все наоборот ". их, когда они поступают плохо, и поскольку существует регресс к среднему, это часть условия, что они статистически наказаны за вознаграждение других и вознаграждены за их наказание. Что-то другое показало плохое воздействие со стороны второго раза, и показало, что эта демонстрация не устранит последствий воздействия извращенных обстоятельств.
Говоря простыми словами, когда кто-то совершает серьезную ошибку, их эффективность позже обычно возвращается к своему среднему уровню. шением и «доказательством» убеждения, что лучше критиковать, чем хвалить (особенно у тех, кто готов критиковать в этот «низкий» момент). В противоположной ситуации, когда кто-то показывает результат выше, его значение также будет тенденцией среднего позже вернуться к своему среднему уровню; изменение будет воспринято как ухудшение. Просто потому, что критика или похвала предшествуют регрессу к среднему, критике или похвалы ложно приписывается причинности. Ошибка регрессии также объясняется в статье Рольфа Добелли Искусство ясно мыслить.
. Политика правоохранительных органов США поддерживает размещение статических или мобильных камер контроля скорости в видимой. аварийные черные пятна. Эта политика была оправдана представлением о соответствующем снижении количества серьезных дорожно-транспортных происшествий после установки камеры. Тем не менее, статистика отметили, что, хотя есть чистая выгода в виде спасенных жизней, неспособность учесть эффекты регрессии к среднему значению приводит к завышению положительных эффектов.
Статистические аналитики давно признали, что эффект возврата к среднему значению в спорте; у них даже есть специальное название: «второкурсник ». Например, Кармело Энтони из НБА Денвер Наггетс провел выдающийся сезон новичка в 2004 году. Он был настолько выдающимся, что от него нельзя было ожидать повторения. это: в 2005 году показатели Энтони упали по сравнению с его сезоном новичка. Причин «спада на втором курсе» предостаточно, поскольку полагается на приспособление и противодействие, но успех новичка, основанный на удаче, является такой же хорошей причиной, как и любая другая. Регрессия к среднему значению спортивных результатов также может объяснить очевидное «обложку журнала Sports Illustrated jinx » и «Madden Curse ». Джонлингер имеет альтернативное название феномена регрессии к среднему: «правило случайности», в то время как Билл Джеймс называет его «принципом оргстекла».
Самые популярные предания используют свое внимание на регрессе к среднему как на объяснении снижения результативности спортсменов от одного сезона к другому, обычно не учитывается тот факт, что такой регресс также может объяснить улучшение результатов. Например, если посмотреть на средний уровень для игроков Высшей лиги бейсбола за один сезон, то те, чей средний уровень был выше среднего значения по лиге, имеют тенденцию к понижению к среднему значению в следующем году. У кого среднее значение было ниже среднего, имеют тенденцию к прогрессу вверх к среднему в следующем году.
Регрессия к среднему просто говорит о том, что после экстремального случайного события, следующее случайное событие, вероятно, будет менее экстремальным. Ни в чем будущее событие не «компенсирует» или «сглаживает» предыдущее событие, хотя это решение в случае ошибки игрока (и в варианте среднего закона ). Точно так же закон больших чисел утверждает, что в долгосрочной перспективе среднее значение будет стремиться к ожидаемому значению, но не делает никаких заявлений об отдельных испытаниях. Например, после серии 10 орлов при подбрасывании справедливой монеты (редкое, экстремальное событие) регрессия к среднему показателю, что следующая серия орлов, вероятно, будет меньше 10, в то время закон больших чисел гласит, что в долгосрочной перспективе это событие, вероятно, будет усреднено, и доля средняя орлов будет стремиться к 1/2. В отличие от этого, ошибка игрока ошибочно предполагает, что монета теперь "должна" выпадать решкой для уравновешивания.
Это определение регрессии к среднему значению, которое близко соответствует исходному использованию сэра Фрэнсиса Гальтона.
Предположим, имеется n точек данных {y i, x i }, где i = 1, 2,…, n. Мы хотим найти уравнение для линии регрессии, т.е. прямой

, которая обеспечит "наилучшее" соответствие точкам данных. (Обратите внимание, что прямая линия может не быть подходящей кривой регрессии для заданных точек данных.) Здесь «лучший» будет пониматься как в подходе наименьших квадратов : такая, которая минимизирует сумму квадрата остатков модели линейной регрессии. Другими словами, числа α и β решают следующую задачу минимизации:
 , где
, где 
Используя исчисление, можно показать, что значения α и β, которые минимизируют цель функции Q равны
![{\ begin {align} {\ hat {\ beta}} = {\ frac {\ sum _ {i = 1} ^ {n} (x_ {i} - {\ bar {x}}) (y_ {i} - {\ bar {y}})} { \ sum _ {i = 1} ^ {n} (x_ {i} - {\ bar {x}}) ^ {2}}} = {\ frac {{\ overline {xy}} - {\ bar {x}) }} {\ bar {y}}} {{\ overline {x ^ {2}}} - {\ bar {x}} ^ {2}}} = {\ frac {\ operatorname {Cov} [x, y ]} {\ operatorname {Var} [x]}} = r_ {xy} {\ frac {s_ {y}} {s_ {x}}}, \\ {\ hat {\ alpha}} = {\ bar {y}} - {\ hat {\ beta}} \, {\ bar {x}}, \ end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4ceb26f542d9dec173923b43d3e9589fef9f36f)
где r xy - коэффициент корреляции выборки между x и y, s x - стандартное отклонение x, а s y, соответственно, стандартное отклонение y. Горизонтальная полоса над стандартным выбором среднего значения этой переменной. Например:
Подстановка приведенные выше выражения для 



, что дает

Это показывает роль r xy в линии регрессии стандартизованных точек.
Если -1 < rxy< 1, then we say that the data points exhibit regression toward the mean. In other words, if linear regression is the appropriate model for a set of data points whose sample correlation coefficient is not perfect, then there is regression toward the mean. The predicted (or fitted) standardized value of y is closer to its mean than the standardized value of x is to its mean.
Пусть X 1, X 2 быть случайными величинами с одинаковыми предельными распределениями со средним μ. В этой форме распределения, двумерное распределение для X 1 и X 2, как говорят, демонстрирует регрессию к среднему, если для каждого числа c>μ, имеем
с обратными неравенствами, выполняемыми для c < μ.
Ниже неформальное описание приведенного выше определения. Рассмотрим совокупность виджетов. Каждый виджет имеет два числа: X 1 и X 2 (скажем, его левый диапазон (X 1) и правый диапазон (X 2)). Предположим, что распределения вероятностей X 1 и X 2 в общей совокупности идентичности, и что средние значения X 1 и X 2 оба μ. Теперь мы берем случайный виджет из совокупности и обозначаем его значение X 1 через c. (Обратите внимание, что c может быть больше, равно или меньше μ.) У нас пока нет доступа к значению X 2 этого виджета. Пусть d обозначает ожидаемое значение X 2 этого конкретного виджета. (т.е. пусть d обозначает среднее значение X 2 всех виджетов в совокупности с X 1 = c.) Если выполняется следующее условие:
тогда мы говорим, что X 1 и X 2 показывают регрессию в сторону среднее .
Это определение близко соответствует нынешнему общепринятому использованию «термина регрессия к среднему», развившемуся от первоначального использования Гальтоном. Он «ограничительный» в смысле, что не каждое двумерное распределение с использованием предельными распределениями.
Если пара (X, Y) случайные величины подчиняются двумерному нормальному распределению , тогда условное среднее E (Y | X) является линейной функцией от X. Коэффициент корреляции r между X и Y вместе с маргинальными средними значениями и дисперсии X и Y, определяют эту линейную зависимость:
![{\ displaystyle {\ frac {E (Y \ mid X) -E [Y]} {\ sigma _ {y}}} = r {\ frac {XE [X]} {\ sigma _ {x}} },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1139b41de03b98d327888dc8a7f0a2c9ab867375)
где E [X] и E [Y] - ожидаемые значения X и Y, соответственно, а σ x и σ y - стандартные отклонения X и Y, соответственно.
Следовательно, условное ожидаемое значение Y, при условии, что X на t стандартных отклонений выше своего среднего (включая случай, когда оно ниже среднего, когда t < 0), is rt standard deviations above the mean of Y. Since |r| ≤ 1, Y is no farther from the mean than X is, as measured in the number of standard deviations.
, следовательно, если 0 ≤ r < 1, then (X, Y) shows regression toward the mean (by this definition).
Следующее определение возврата к среднему было предложено Самуэльсом в качестве альтернативы более ограниченному определению регрессии к среднему выше.
Пусть X 1, X 2 быть случайными величинами с идентичными маргинальными распределениями со средним μ. В этой формализации двумерное распределение для X 1 и X 2 Говорят, что демонстрирует возврат к среднему, если для каждого числа c мы имеем
Это определение является «общим» в том смысле, что каждое двумерное распределение с идентичными маргинальными распределениями демонстрирует возврат к среднему.