Принцип Харди - Вайнберга

принцип в генетике

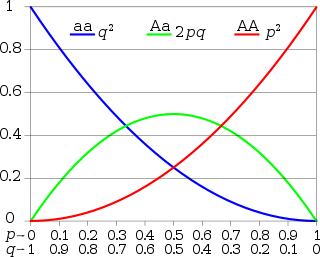
Пропорции Харди - Вайнберга для двух аллелей : горизонтальная ось показывает две частоты аллелей p и q, а вертикальная ось показывает ожидаемые частоты генотипов. Каждая линия показывает один из трех отдельных генотипов.

В популяционной генетике используется принцип Харди - Вайнберга, также известный как равновесие Харди - Вайнберга, модель, теорема, или закон, гласит, что частоты аллелей и генотипов в процессе роста остаются постоянными от поколения к поколению в отсутствие других эволюционных влияний. Эти влияния включают генетический дрейф, выбор партнера, ассортативное спаривание, естественный отбор, половой отбор, мутация, поток генов, мейотический драйв, генетический автостоп, узкое место популяции, эффект основателя и инбридинг.

В простейшем случае одного локуса с двумя аллелями, обозначенными A и a, с частотами f(A) = p и f(a) = q, соответственно ожидаемые частоты генотипов при случайном скрещивании равны f(AA) = p для AA гомозигот, f(aa) = q для гомозигот aa, и f(Aa) = 2pq для гетерозигот. В отсутствие отбора, мутации, генетического дрейфа или других частотах аллелей p и q постоянны между поколениями, поэтому равновесие достигается.

Принцип назван в честь G. Х. Харди и Вильгельм Вайнберг, которые осуществляли это математически. Статья Харди была сосредоточена на опровержении широко распространенного тогда мнения о том, что доминантный аллель автоматически имеет тенденцию к увеличению частоты; сегодня путаница между доминированием и отбором встречается реже. Сегодня тесты на частоту генотипов Харди - Вайнберга используются в основном для проверки стратификации населения и других форм неслучайного спаривания.

• 1 Деривация
• 2 Отклонения от равновесия Харди - Вайнберга
• 3 Половая связь
• 4 Обобщения
  • 4.1 Обобщение для более чем двух аллелей
  • 4.2 Обобщение для полиплоидии
  • 4.3 Полное обобщение
• 5 Тесты значимости отклонения
  • 5.1 Пример $\chi \; 2\; \{\backslash \; displaystyle\; \backslash \; chi\; ^\; \{2\}\}$тест отклонения
  • 5.2 Точный тест Фишера (вероятностный тест)
• 6 Тесты на эквивалентность
• 7 Коэффициент инбридинга
• 8 История
  • 8.1 Вывод результатов Харди
  • 8.2 Числовой пример
    • 8.2.1 Оценка распределения генотипов
    • 8.2.2 Оценка Несущая частота
• 9 Графическое представление
• 10 См. Также
• 11 Примечания
• 12 Ссылки
  • 12.1 Цитаты
  • 12.2 Источники
• 13 Внешние ссылки

Рассмотрим популяцию однодомных диплоидов, где каждый производит мужские и женские гаметы с одинаковой величиной и имеет два аллеля в каждом локусе гена. Организмы размножаются путем случайного объединения гамет (популяционная модель «генофонда»). Локус в этой поплавке имеет два аллеля, A и a, которые встречаются с начальными частотами f 0 (A) = p и f 0 (a) = q, соответственно. Частоты аллелей в каждом поколении путем объединения аллелей из каждого генотипа одного поколения с ожидаемым вкладом гомозиготного и гетерозиготного генотипов, которые равны 1 и 1/2 соответственно:

$ft\; (A)\; =\; ft\; (AA)\; +\; 1\; 2\; ступени\; (Aa)\; \{\backslash \; displaystyle\; f\_\; \{t\}\; (\{\backslash \; text\; \{A\}\})\; =\; f\_\; \{t\}\; (\{\backslash \; text\; \{AA\}\})\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; f\_\; \{t\}\; (\{\backslash \; text\; \{Aa\}\})\}$

(1)

$ft\; (a)\; =\; ft\; (aa)\; +\; 1\; 2\; ft\; (Aa)\; \{\backslash \; displaystyle\; f\_\; \{t\}\; (\{\backslash \; text\; \{a\}\})\; =\; f\_\; \{t\}\; (\{\backslash \; text\; \{aa\}\})\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; f\_\; \{t\}\; (\{\backslash \; text\; \{Aa\}\})\}$

(2)

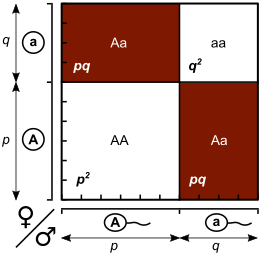
Длина p, q соответствует частотам аллелей (здесь p = 0,6, q = 0,4). Затем область прямоугольника представляет собой частоты генотипов (таким, AA: Aa: aa = 0,36: 0,48: 0,16).

Различные способы формирования генотипов следующего поколения могут быть показаны в квадрате Пеннета, где доля каждого генотипа равна произведению частот аллелей строки и столбца текущего поколения.

Таблица 1: Квадрат Пеннета для Харди - Вайнберга

		Самок
		A (p)	a (q)
Самцов	A (p)	AA (p)	Aa (pq)
	a (q)	Aa (qp)	aa (q)

Сумма записи - p + 2pq + q = 1, так как частоты генотипов должны в сумме равняться единице.

Заметим еще раз, что, поскольку p + q = 1, биномиальное разложение (p + q) = p + 2pq + q = 1 дает те же отношения.

Суммируя элементы квадрата Пеннета или биноми разложения, мы получаем ожидаемые пропорции генотипов среди потомков после одного поколения:

$f\; 1\; (AA)\; =\; p\; 2\; =\; f\; 0\; (A)\; 2\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\{\backslash \; text\; \{AA\}\})\; =\; p\; ^\; \{2\}\; =\; f\_\; \{0\}\; (\{\backslash \; text\; \{A\}\})\; ^\; \{2\}\}$

(3)

$е\; 1\; (Aa)\; =\; pq\; +\; qp\; =\; 2\; pq\; =\; 2\; f\; 0\; (A)\; f\; 0\; (a)\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\{\backslash \; text\; \{Aa\}\})\; =\; pq\; +\; qp\; =\; 2pq\; =\; 2f\_\; \{0\}\; (\{\backslash \; text\; \{A\; \}\})\; f\_\; \{0\}\; (\{\backslash \; text\; \{a\}\})\}$

(4)

$f\; 1\; (aa)\; =\; q\; 2\; =\; f\; 0\; (a)\; 2\; \{\backslash \; displaystyle\; f\_\; \{1\}\; (\{\; \backslash \; text\; \{aa\}\})\; =\; q\; ^\; \{2\}\; =\; f\_\; \{0\}\; (\{\backslash \; text\; \{a\}\})\; ^\; \{2\}\}$

(5)

Эти частоты определяют равновесие Харди - Вайнберга. Следует отметить, что частоты генотипов после первого поколения не обязательно должны совпадать с частотами генотипов от начального поколения, например, f 1 (AA) ≠ f 0 (AA). Однако частоты генотипов для всех будущих времен будут равны частотам Харди - Вайнберга, например f t (AA) = f 1 (AA) для t>1. Это следует из того, что частоты генотипов следующего поколения зависят от частот аллелей текущего поколения, которые вычисляются по уравнениям (1) и (2), сохраняются от исходного поколения:

$f\; 1\; (A)\; =\; f\; 1\; (\; AA)\; +\; 1\; 2\; f\; 1\; (Aa)\; =\; p\; 2\; +\; pq\; =\; p\; (p\; +\; q)\; =\; p\; =\; f\; 0\; (A)\; f\; 1\; (a)\; =\; f\; 1\; (aa)\; +\; 1\; 2\; f\; 1\; (Aa)\; =\; q\; 2\; +\; pq\; =\; q\; (p\; +\; q)\; =\; q\; =\; f\; 0\; (a)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; f\_\; \{1\}\; (\{\backslash \; text\; \{A\}\})\; =\; f\_\; \{1\}\; (\{\backslash \; текст\; \{AA\}\})\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; f\_\; \{1\}\; (\{\backslash \; text\; \{Aa\}\})\; =\; p\; ^\; \{2\}\; +\; pq\; =\; p\; (p\; +\; q)\; =\; p\; =\; f\_\; \{\; 0\}\; (\{\backslash \; text\; \{A\}\})\; \backslash \backslash \; f\_\; \{1\}\; (\{\backslash \; text\; \{a\}\})\; =\; f\_\; \{1\}\; (\{\backslash \; text\; \{aa\}\})\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\; \}\}\; f\_\; \{1\}\; (\{\backslash \; text\; \{Aa\}\})\; =\; q\; ^\; \{2\}\; +\; pq\; =\; q\; (p\; +\; q)\; =\; q\; =\; f\_\; \{0\}\; (\{\backslash \; text\; \{a\}\})\; \backslash \; конец\; \{выравнивается\; \}\}\}$

Для более общих случаев двудомных диплоидов [организмы либо самцы, либо самки], которые воспроизводятся путем случайного спаривания особей, это необходимо для расчета частот генотипов из девяти исполнителей спариваний между каждым родительским генотипом (AA, Aa и aa) любог о пола, взвешенных по ожидаемому генотипу роли каждого спаривания. Эквивалентно, можно рассмотреть шесть уникальных диплоид-диплоидных комбинаций:

$[(AA,\; AA),\; (AA,\; Aa),\; (AA,\; aa),\; (Aa,\; Aa),\; (Aa,\; aa),\; (aa,\; aa))]\; \{\backslash \; displaystyle\; \backslash \; left\; [(\{\backslash \; text\; \{AA\}\},\; \{\backslash \; text\; \{AA\}\}),\; (\{\backslash \; text\; \{AA\}\},\; \{\backslash \; text\; \{Aa\}\}),\; (\{\backslash \; text\; \{AA\; \}\},\; \{\backslash \; text\; \{aa\}\}),\; (\{\backslash \; text\; \{Aa\}\},\; \{\backslash \; text\; \{Aa\}\}),\; (\{\backslash \; text\; \{Aa\}\},\; \{\backslash \; text\; \{aa\}\}),\; (\{\; \backslash \; text\; \{aa\}\},\; \{\backslash \; text\; \{aa\}\})\; \backslash \; right]\}$

и строит квадрат Пеннета для каждого, чтобы вычислить его вклад в генотипы следующего поколения. Эти вклады взвешиваются в соответствии с вероятностью каждой диплоидно-диплоидной комбинации, которая следует полиномиальному распределению с k = 3. Например, вероятность брачной комбинации (AA, aa) составляет 2 f t (AA) f t (aa), и это может привести только к генотипу Aa: [0,1,0]. В целом, результирующие частоты генотипов рассчитываются как:

$[ft + 1 (AA), ft + 1 (Aa), ft + 1 (aa)] = = ft (AA) ft (AA) [1, 0, 0 ] + 2 ft (AA) ft (Aa) [1 2, 1 2, 0] + 2 ft (AA) ft (aa) [0, 1, 0] + ft (Aa) ft (Aa) [1 4, 1 2, 1 4] + 2 ft (Aa) ft (aa) [0, 1 2, 1 2] + ft (aa) ft (aa) [0, 0, 1] = [(ft (AA) + 1 2 ft (Aa)) 2, 2 (ft (AA) + 1 2 ft (Aa)) (ft (aa) + 1 2 ft (Aa)), (ft (aa) + 1 2 ft (Aa)) 2 ] = [ft (A) 2, 2 ft (A) ft (a), ft (a) 2] {\ displaystyle {\ begin {align} \ left [f_ {t + 1} ({\ text {AA }}), f_ {t + 1} ({\ text {Aa}}), f_ {t + 1} ({\ text {aa}}) \ right] = \\ \ qquad = f_ {t} ( {\ text {AA}}) f_ {t} ({\ text {AA}}) \ left [1,0,0 \ right] + 2f_ {t} ({\ text {AA}}) f_ {t} ({\ text {Aa}}) \ left [{\ tfrac {1} {2}}, {\ tfrac {1} {2}}, 0 \ right] + 2f_ {t} ({\ text {AA} }) f_ {t} ({\ text {aa}}) \ left [0,1,0 \ right] \\ \ qquad \ qquad + f_ {t} ({\ text {Aa}}) f_ {t } ({\ text {Aa}}) \ left [{\ tfrac {1} {4}}, {\ tfrac {1} {2}}, {\ tfrac {1} {4}} \ right] + 2 ебат ь {т} ({\ text {Aa}}) f_ {t} ({\ text {aa}}) \ left [0, {\ tfrac {1} {2}}, {\ tfrac {1} {2 }} \ right] + f_ {t} ({\ text {aa}}) f_ {t} ({\ text {aa}}) \ left [0,0,1 \ right] \\ \ qquad = \ left [\ left (f_ {t} ({\ text {AA}}) + {\ tfrac {1} {2}} f_ {t} ({\ text {Aa}}) \ right) ^ {2}, 2 \ left (f_ {t} ({\ text {AA}}) + {\ tfrac {1} {2}} f_ {t} ({\ text {Aa}}) \ right) \ left (f_ {t } ({\ text {aa}}) + {\ tfrac {1} {2}} f_ {t} ({\ text {Aa}}) \ right), \ left (f_ {t} ({\ text { aa}}) + {\ tfrac {1} {2}} f_ {t} ({\ text {Aa}}) \ right) ^ {2} \ right] \\ \ qquad = \ left [f_ {t } ({\ text {A}}) ^ {2}, 2f_ {t} ({\ text {A}}) f_ {t} ({\ text {a}}), f_ {t} ({\ text {a}}) ^ {2} \ right] \ end {align}}}$

Как и раньше, можно показать, что частоты аллелей в момент времени t + 1 равны частотам в момент времени t, а значит, постоянны во времени.. Точно так же частоты генотипов зависят только от частот аллелей, и поэтому после времени t = 1 также остаются постоянными во времени.

Если у однодомных или раздельнополых организмов пропорций аллелей или генотипов изначально неодинаковы для обоих полов, можно показать, что постоянные пропорции достигаются после одного генерация случайного спаривания. Если раздельнополые организмы гетерогаметны и локус расположен на Х-хромосоме, можно показать, что если частоты аллелей изначально неодинаковы у двух полов [например, женщины XX и мужчины XY, как у людей], f′ (a) в гетерогаметных сексуальных «погонях» f(a) в гомогаметный пол предыдущего поколения, пока не достигнуто равновесие при средневзвешенном значении двух исходных частот.

В основе равновесия Харди-Вайнберга лежат следующие семь допущений:

• организмы диплоидны
• происходит только половое размножение
• поколения не пересекаются
• случайное спаривание
• размер популяции бесконечно большой
• частоты аллелей равны у полов
• миграция отсутствует, ген поток, примесь, мутация или отбор

Нарушение предположений Харди - Вайнберга может вызвать отклонения от ожидания. Как это влияет на население, зависит от допущений, которые нарушаются.

• Случайная вязка. HWP утверждает, что популяция будет иметь данные генотипических частот (так называемые пропорции Харди - Вайнберга) после поколения случайных спариваний в популяции. Когда предположение о случайном скрещивании нарушается, популяция не будет иметь пропорции Харди - Вайнберга. Распространенной причиной неслучайного спаривания является инбридинг, который вызывает увеличение гомозиготности для всех генов.

Если популяция нарушает одно из следующих предположений, популяция может быть пропорции Харди - Вайнберга сохраняются в каждом поколении, но частоты аллелей со временем будут меняться.

• Выбор, как правило, часто меняет частоты аллелей, довольно быстро. Хотя направленный отбор в конечном итоге приводит к потере всех аллелей, кроме предпочтительного (если один аллель является не доминирующим, и в этом случае рецессивные аллели могут выжить при низких частотах), некоторые формы отбора, такие как балансирующий отбор, приводит к равновесию без потерь аллелей.
• Мутация будет иметь очень тонкий эффект на частоты аллелей. Частота мутаций составляет от 10 до 10, и изменение частоты аллелей будет, самое большее, в том же порядке. Повторяющаяся мутация будет поддерживать аллели в пополнении, даже если против них будет строгий отбор.
• Миграция генетически связывает две или более популяции вместе. В целом частоты аллелей становятся более однородными среди популяций. Некоторые модели миграции по своей сути включают неслучайное спаривание (эффект Валунда, например). Для этих моделей пропорций Харди - Вайнберга обычно недействительны.
• Небольшой размер популяции может вызвать случайное изменение частот аллелей. Это происходит из-за эффекта выборки и называется генетическим дрейфом. Эффекты выборки наиболее важны, когда аллель присутствует в небольшом количестве копий.

Если ген A сцеплен с полом, гетерогаметный пол (например, самцы млекопитающих; птичьи самки) имеют только одну копию гена (и называются гемизиготными), в то время как гомогаметный пол (например, человеческие самки) имеет две копии. Частоты генотипов в равновесии: p и q для гетерогаметного пола, но p, 2pq и q для гомогаметного пола.

Например, у людей красно-зеленая дальтонизм является Х-сцепленным рецессивным признаком. У западноевропейских мужчин этот признак показывает примерно 1 из 12 (q = 0,083), тогда как он рассматривает примерно 1 из 200 женщин (0,005 по сравнению с q = 0,007), что очень близко к пропорциям Харди - Вайнберга.

Если популяция объединяется с мужчинами и женщинами с разной аллелей в каждой субпопуляции (мужчины или женщины), то частота аллелей мужской популяции будет соответствовать пропорциям аллелей женской популяции, потому что каждый сын получает свою Х-хромосому от матери. Население очень быстро приходит к равновесию.

Простой вывод, приведенный выше, может быть обобщен для более чем двух аллелей и полиплоидии.

Обобщение для более чем двух аллелей

Квадрат Пеннета для трехаллельного случая ( слева) и четырехаллельный случай (справа). Белые области - гомозиготы. Цветные области - гетерозиготы.

Учитывайте частоту дополнительных аллелей, r. С двумя аллелями - это биномиальное расширение для (p + q), и, таким образом, случай с тремя аллелями - это триномиальное расширение (p + q + r).

$(p\; +\; q\; +\; r)\; 2\; =\; p\; 2\; +\; q\; 2\; +\; r\; 2\; +\; 2\; pq\; +\; 2\; pr\; +\; 2\; qr\; \{\backslash \; displaystyle\; (p\; +\; q\; +\; r)\; ^\; \{2\}\; =\; p\; ^\; \{2\}\; +\; q\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; +\; 2pq\; +\; 2pr\; +\; 2qr\; \backslash ,\}$

В целом, рассмотрим аллели A 1,..., A n задается частотами аллелей от p 1 до p n;

$(p\; 1\; +\; \cdots \; +\; pn)\; 2\; \{\backslash \; displaystyle\; (p\_\; \{1\}\; +\; \backslash \; cdots\; +\; p\_\; \{n\})\; ^\; \{2\}\; \backslash ,\}$

дает для всех гомозигот :

$f\; (A\; i\; A\; i)\; =\; pi\; 2\; \{\backslash \; displaystyle\; f\; (A\_\; \{i\}\; A\_\; \{i\})\; =\; p\_\; \{i\}\; ^\; \{2\}\; \backslash ,\}$

и для всех гетерозигот :

$f\; (A\; i\; A\; j)\; =\; 2\; pipj\; \{\backslash \; displaystyle\; f\; (A\_\; \{i\}\; A\_\; \{j\})\; =\; 2p\_\; \{i\}\; p\_\; \{j\}\; \backslash ,\}$

Обобщение для полиплоидии

Принцип Харди-Вайнберга также может быть обобщен на полиплоидные системы, то есть для организмов, которые имеют более двух копий каждой хромосомы. Рассмотрим снова только два аллеля. Диплоидный случай - это биномиальное разложение из:

$(p\; +\; q)\; 2\; \{\backslash \; displaystyle\; (p\; +\; q)\; ^\; \{2\}\; \backslash ,\}$

и, следовательно, полиплоидный случай - это полиномиальное разложение из:

$(p\; +\; q)\; c\; \{\backslash \; displaystyle\; (p\; +\; q)\; ^\; \{c\}\; \backslash ,\}$

, где c - плоидность, например с тетраплоидом (c = 4):

Таблица 2: Ожидаемые частоты генотипов для тетраплоидии

Генотип	Частота
AAAA	$p\; 4\; \{\backslash \; displaystyle\; p\; ^\; \{4\}\}$
AAAa	$4\; p\; 3\; q\; \{\backslash \; displaystyle\; 4p\; ^\; \{3\}\; q\}$
AAaa	$6\; p\; 2\; q\; 2\; \{\backslash \; displaystyle\; 6p\; ^\; \{2\}\; q\; ^\; \{2\}\}$
AAaa	$4\; pq\; 3\; \{\backslash \; displaystyle\; 4pq\; ^\; \{3\}\}$
aaaa	$q\; 4\; \{\backslash \; displaystyle\; q\; ^\; \{4\}\}$

От того, является ли организм «истинным» тетраплоидом или амфидиплоидом, будет зависеть, как Потребуется много времени, чтобы население достигло равновесия Харди - Вайнберга.

Полное обобщение

для $n\; \{\backslash \; displaystyle\; n\}$различных аллелей в $c\; \{\backslash \; displaystyle\; c\}$-плоидов, частоты генотипов в равновесии Харди - Вайнберга задаются отдельными членами в полиномиальном разложении из $(p\; 1\; +\; \cdots \; +\; pn)\; c\; \{\backslash \; displaystyle\; (p\_\; \{1\}\; +\; \backslash \; cdots\; +\; p\_\; \{n\})\; ^\; \{c\}\}$:

$(p\; 1\; +\; \cdots \; +\; pn)\; c\; =\; \sum \; k\; 1,\dots ,\; kn\; \in \; N:\; k\; 1\; +\; \cdots \; +\; kn\; =\; c\; (ck\; 1,\dots ,\; kn)\; p\; 1\; К\; 1\; \cdots \; pnkn\; \{\backslash \; displaystyle\; (p\_\; \{1\}\; +\; \backslash \; cdots\; +\; p\_\; \{n\})\; ^\; \{c\}\; =\; \backslash \; sum\; \_\; \{k\_\; \{1\},\; \backslash \; ldots,\; k\_\; \{n\}\; \backslash \; \backslash \; in\; \backslash \; mathbb\; \{N\}:\; k\_\; \{1\; \}\; +\; \backslash \; cdots\; +\; k\_\; \{n\}\; =\; c\}\; \{c\; \backslash \; select\; k\_\; \{1\},\; \backslash \; ldots,\; k\_\; \{n\}\}\; p\_\; \{1\}\; ^\; \{k\_\; \{1\}\}\; \backslash \; cdots\; p\_\; \{n\}\; ^\; \{k\_\; \{\; n\}\}\}$

Тестирование отклонения от HWP обычно выполняется с помощью критерия хи-квадрат Пирсона с использованием наблюдаемых частот генотипов, полученных из данных и ожидаемых значений генотипов, полученных, полученных с помощью HWP. Для систем с большим количеством аллелей это может привести к получению данных с множеством пустых генотипов и низким числом генотипов, потому что в выборе часто не хватает индивидов для адекватного представления всех классов генотипов. Если это так, предположение асимптотики для распределения хи-квадрат больше не будет, и может потребоваться использовать формулу точного критерия Фишера., для решения которой требуется компьютер . Совсем недавно был предложен ряд методов MCMC проверки отклонений от HWP (Guo Thompson, 1992; Wigginton et al. 2005)

Пример $\chi \; 2\; \{\backslash \; displaystyle\; \backslash \; chi\; ^\; \{2\; \}\}$тест на отклонение

Эти данные взяты из E. B. Ford (1971) на алой тигровой мотыльке, для которой были зарегистрированы фенотипы выборки популяции. Предполагается, что различие между генотипом и фенотипом пренебрежимо мало. нулевая гипотеза состоит в том, что популяция находится в пропорциях Харди-Вайнберга, а альтернативная гипотеза заключается в том, что популяция не имеет пропорций Харди-Вайнберга.

Таблица 3: Пример расчета по принципу Харди - Вайнберга

Фенотип	Белые пятна (AA)	Промежуточные (Aa)	Небольшие пятна (aa)	Всего
Число	1469	138	5	1612

Отсюда можно вычислить частоты аллелей:

$p\; =\; 2\; \times \; набл\; (AA)\; +\; набл\; (Aa)\; 2\; \times \; (набл\; (AA)\; +\; набл\; (Aa)\; +\; набс\; (aa))\; =\; 1469\; \times \; 2\; +\; 138\; 2\; \times \; (1469\; +\; 138\; +\; 5)\; =\; 3076\; 3224\; =\; 0,954\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; p\; =\; \{2\; \backslash \; times\; \backslash \; mathrm\; \{obs\}\; (\{\backslash \; text\; \{AA\}\})\; +\; \backslash \; mathrm\; \{obs\}\; (\{\backslash \; text\; \{Aa\}\})\; \backslash \; более\; 2\; \backslash \; times\; (\backslash \; mathrm\; \{obs\}\; (\{\backslash \; текст\; \{AA\}\})\; +\; \backslash \; mathrm\; \{obs\}\; (\{\backslash \; text\; \{Aa\}\})\; +\; \backslash \; mathrm\; \{obs\}\; (\{\backslash \; text\; \{aa\}\}))\}\; \backslash \backslash \backslash \backslash \; =\; \{1469\; \backslash \; times\; 2\; +\; 138\; \backslash \; более\; 2\; \backslash \; раз\; (1469\; +\; 138\; +\; 5)\}\; \backslash \backslash \backslash \backslash \; =\; \{3076\; \backslash \; более\; 3224\}\; \backslash \backslash \backslash \backslash \; =\; 0,954\; \backslash \; конец\; \{выровнено\}\}$

и

$q\; =\; 1\; -\; p\; =\; 1\; -\; 0,954\; =\; 0,046\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; q\; =\; 1-p\; \backslash \backslash \; =\; 1-0,954\; \backslash \backslash \; =\; 0,046\; \backslash \; end\; \{align\}\}\}$

Итак, Харди– Вайнберг математическое ожидание равно:

$E\; xp\; (AA)\; =\; p\; 2\; n\; =\; 0,9\; 5\; 4\; 2\; \times \; 1612\; =\; 1467,4\; E\; xp\; (Aa)\; =\; 2\; pqn\; =\; 2\; \times \; 0,954\; \times \; 0,046\; \times \; 1612\; =\; 141,2\; E\; xp\; (aa)\; =\; q\; 2\; n\; =\; 0,046\; 2\; \times \; 1612\; =\; 3,4\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; \backslash \; mathrm\; \{Exp\}\; (\{\backslash \; text\; \{AA\}\})\; =\; p\; ^\; \{2\}\; n\; =\; 0,954\; ^\; \{2\}\; \backslash \; times\; 1612\; =\; 1467,4\; \backslash \backslash \backslash \; mathrm\; \{Exp\}\; (\{\backslash \; текст\; \{Aa\}\})\; =\; 2pqn\; =\; 2\; \backslash \; times\; 0,954\; \backslash \; times\; 0,046\; \backslash \; times\; 1612\; =\; 141,2\; \backslash \backslash \backslash \; mathrm\; \{Exp\}\; (\{\backslash \; text\; \{aa\}\})\; =\; q\; ^\; \{2\}\; n\; =\; 0,046\; ^\; \{2\}\; \backslash \; times\; 1612\; =\; 3,4\; \backslash \; end\; \{align\}\}\}$

критерий хи-квадрат Пирсона утверждает:

$\chi \; 2\; знак\; равно\; \sum \; (O\; -\; E)\; 2\; E\; =\; (1469\; -\; 1467,4)\; 2\; 1467,4\; +\; (138\; -\; 141,2)\; 2\; 141,2\; +\; (5\; -\; 3,4)\; 2\; 3,4\; =\; 0,001\; +\; 0,073\; +\; 0,756\; =\; 0,83\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\; \}\; \backslash \; chi\; ^\; \{2\}\; =\; \backslash \; sum\; \{(OE)\; ^\; \{2\}\; \backslash \; over\; E\}\; \backslash \backslash \; =\; \{(1469-1467,4)\; ^\; \{2\}\; \backslash \; over\; 1467,4\}\; +\; \{(138-\; 141,2)\; ^\; \{2\}\; \backslash \; более\; 141,2\}\; +\; \{(5-3,4)\; ^\; \{2\}\; \backslash \; более\; 3,4\}\; \backslash \backslash \; =\; 0,001\; +\; 0,073\; +\; 0,756\; \backslash \backslash \; =\; 0,83\; \backslash \; конец\; \{выровнено\}\}\}$

Имеется 1 степень свободы (степень свободы для теста на пропорции Харди - Вайнберга: # генотипов - # аллелей). 5% уровень значимости для 1 степени свободы составляет 3,84, а поскольку значение χ меньше этого, нулевая гипотеза о том, что популяция находится в частотах Харди - Вайнберга, составляет не отклонено.

Точный критерий Фишера (вероятностный тест)

Точный тест Фишера могут использовать условия для тестирования пропорций Харди - Вайнберга. Тест тест зависит от частот аллелей p и q, проблему можно рассматривать как проверка на правильное количество гетерозигот. Таким образом, гипотеза о пропорциях Харди-Вайнберга отвергается, если количество гетерозигот слишком велико или слишком мало. Условные вероятности гетерозиготы с учетом частот аллелей в Emigh (1980) как

$вероятность\; \; [n\; 12\; |\; n\; 1]\; =\; (nn\; 11,\; n\; 12,\; n\; 22)\; (2\; nn\; 1,\; n\; 2)\; 2\; n\; 12,\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{prob\}\; [n\_\; \{12\}\; |\; n\_\; \{1\}]\; =\; \{\backslash \; frac\; \{\backslash \; binom\; \{n\}\; \{n\_\; \{11\},\; n\_\; \{12\},\; n\_\; \{22\}\}\}\; \{\backslash \; binom\; \{2n\}\; \{n\_\; \{1\},\; n\_\; \{2\}\}\}\; \}\; 2\; ^\; \{n\_\; \{12\}\},\}$

где n 11, n 12, n 22 - наблюдаемые числа трех генотипов, AA, Aa и aa, соответственно, и n 1 - аллелей A, где $n\; 1\; =\; 2\; n\; 11\; +\; n\; 12\; \{\backslash \; displaystyle\; n\_\; \{1\}\; =\; 2n\_\; \{11\}\; +\; n\_\; \{12\}\}$.

Пример Используя один из примеров из Emigh (1980), мы можем рассмотреть случай, когда n = 100 и p = 0,34. Возможные наблюдаемые гетерозиготы и их точный уровень значимости в таблице 4.

Таблица 4: Пример точного критерия Фишера для n = 100, p = 0,34.

Количество гетерозигот	Уровень значимости
0	0,000
2	0,000
4	0,000
6	0,000
8	0,000
10	0,000
12	0,000
14	0,000
16	0,000
18	0,001
20	0,007
22	0,034
34	0,067
24	0,151
32	0,291
26	0,474
30	0,730
28	1.000

Используя эту таблицу, нужно найти уровень значимости теста на основе наблюдаемого количества гетерозигот. Например, если наблюдается 20 гетерозигот, уровень значимости для теста составляет 0,007. Как это типично для точного теста Фишера для небольших выборок, градация уровней значимости довольно грубая.

Однако такая таблица должна создаваться для каждого эксперимента, поскольку зависит от n, так и от p.

Тесты эквивалентности разработаны для того, чтобы установить соответствующее соответствие наблюдаемых частот генотипов Харди-Вайнберга. Пусть $M\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{M\}\}\}$обозначает семейство распределений генотипов в предположении равновесия Харди Вайнберга. Расстояние между распределением генотипов $p\; \{\backslash \; displaystyle\; p\}$и равновесием Харди Вайнберга определяется как $d\; (p,\; M)\; =\; min\; q\; \in \; M\; d\; (p,\; q)\; \{\backslash \; displaystyle\; d\; (\; p,\; \{\backslash \; mathcal\; \{M\}\})\; =\; \backslash \; min\; \_\; \{q\; \backslash \; in\; \{\backslash \; mathcal\; \{M\}\}\}\; d\; (p,\; q)\}$, где $d\; \{\backslash \; displaystyle\; d\}$- некоторое расстояние. Задача теста на эквивалентность задается формулой $H\; 0\; =\; \{d\; (p,\; M)\; \ge \; \epsilon \}\; \{\backslash \; displaystyle\; H\_\; \{0\}\; =\; \backslash \; \{d\; (p,\; \{\backslash \; mathcal\; \{M\}\})\; \backslash \; geq\; \backslash \; varepsilon\; \backslash \}\; \}$и , где $\epsilon >0\; \{\backslash \; displaystyle\; \backslash \; varepsilon>0\}$является параметром допуска. Если гипотеза $.\; H\; 0\; \{\backslash \; displaystyle\; H\_\; \{0\}\}$можно отклонить, тогда популяция с высокой вероятностью близка к равновесию Харди Вайнберга. Тесты эквивалентности для двуаллельного случая разработаны, в Wellek (2004). множественных аллелей предложены в Ostrovski (2020).