 Планирование экспериментов с полным факторным планом (слева), поверхность отклика с полиномом второй степени (справа)
Планирование экспериментов с полным факторным планом (слева), поверхность отклика с полиномом второй степени (справа) план экспериментов (DOE, DOX или экспериментальный план ) - это план любой задачи, целью которого является описание и объяснение вариации информации в условиях, которые, как предполагается, отражают вариацию. Этот термин обычно ассоциируется с экспериментами, в которых план вводит условия, которые непосредственно влияют на вариацию, но также может относиться к плану квазиэкспериментов, в которых естественный для наблюдения выбраны условия, влияющие на изменение.
В своей простейшей форме эксперимент направлен на прогнозирование результата путем введения изменения предварительных условий, которое представлено одной или несколькими независимыми переменными, также называемыми «входными переменными». или «переменные-предикторы». Обычно предполагается, что изменение одной или нескольких независимых переменных приводит к изменению одной или нескольких зависимых переменных, также называемых «выходными переменными» или «переменными ответа». План эксперимента может также определять контрольные переменные, которые должны оставаться постоянными, чтобы внешние факторы не влияли на результаты. Планирование эксперимента включает не только выбор подходящих независимых, зависимых и управляющих переменных, но и планирование проведения эксперимента в статистически оптимальных условиях с учетом ограничений доступных ресурсов. Существует несколько подходов к определению набора проектных точек (уникальных комбинаций настроек независимых переменных), которые будут использоваться в эксперименте.
Основные проблемы при разработке эксперимента включают установление достоверности, надежности и воспроизводимости. Например, эти проблемы можно частично решить, тщательно выбрав независимую переменную, снизив риск ошибки измерения и обеспечив достаточно подробное описание метода. Связанные с этим проблемы включают достижение соответствующих уровней статистической мощности и чувствительности.
Правильно спланированные эксперименты расширяют знания в естественных, социальных и технических науках. Другие приложения включают маркетинг и разработку политики. Изучение плана экспериментов является важной темой в метанауке.
Теория статистического вывода была разработана Чарльзом С. Пирсом в «Иллюстрациях логики науки » ( 1877–1878) и «Теория вероятного вывода » (1883), две публикации, в которых подчеркивалась важность рандомизационного вывода в статистике.
Чарльз С. Пирс случайным образом распределил добровольцев по слепому, плану повторных измерений для оценки их способности различать веса. Эксперимент Пирса вдохновил других исследователей в области психологии и образования, которые разработали исследовательскую традицию рандомизированных экспериментов в лабораториях и специализированных учебниках в 1800-х годах.
Чарльз С. Пирс также внес свой вклад первая англоязычная публикация по оптимальному дизайну для регрессионных моделей в 1876 году. Новаторский оптимальный дизайн для полиномиальной регрессии был предложен Жергонном в 1815 году. В 1918 году Кирстин Смит опубликовала оптимальные планы для многочленов шестой степени (и меньше).
Использование последовательности экспериментов, дизайн каждого из которых может зависеть от результатов предыдущих экспериментов, включая возможное решение прекратить эксперименты, находится в рамках последовательного анализа, поле, которое было впервые открыто Абрахамом Уолдом в контексте последовательной проверки статистических гипотез. Она Человек Чернов написал обзор оптимальных последовательных планов, а адаптивные планы были исследованы С. Заксом. Одним из специфических типов последовательного дизайна является «двурукий бандит», обобщенный на многорукий бандит, ранняя работа над которым была выполнена Гербертом Роббинсом в 1952 году.
Методология планирования экспериментов была предложена Рональдом Фишером в его новаторских книгах: Организация полевых экспериментов (1926) и План экспериментов (1935 г.). Большая часть его новаторских работ была связана с применением статистических методов в сельском хозяйстве. В качестве обыденного примера он описал, как проверить дама, дегустирующая чай гипотезу, о том, что некая женщина может различать только по вкусу, было ли молоко или чай сначала помещено в чашку. Эти методы широко применялись в биологических, психологических и сельскохозяйственных исследованиях.
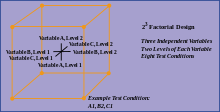 Пример ортогонального факторного плана
Пример ортогонального факторного плана 
Этот пример дизайнерских экспериментов приписывается Гарольду Хотеллингу и основан на примерах из Фрэнка Йейтса. Эксперименты, разработанные в этом примере, включают комбинаторные планы.
. Вес восьми объектов измеряется с помощью чашечных весов и набора стандартных гирь. При каждом взвешивании измеряется разница в весе между объектами на левой чашке и любыми объектами на правой чаше весов путем добавления откалиброванных гирь к более легкой чаше до тех пор, пока весы не придут в равновесие. Каждое измерение имеет случайную ошибку. Средняя ошибка равна нулю; стандартное отклонение распределения вероятностей ошибок - это одно и то же число σ при разных взвешиваниях; ошибки на разных взвешиваниях независимы. Обозначим истинные веса через

Мы рассматриваем два разных эксперимента:


![{\ displaystyle {\ begin {align} { \ widehat {\ theta}} _ {2} = {\ frac {Y_ {1} + Y_ {2} -Y_ {3} -Y_ {4} + Y_ {5} + Y_ {6} -Y_ {7 } -Y_ {8}} {8}}. \\ [5pt] {\ widehat {\ theta}} _ {3} = {\ frac {Y_ {1} + Y_ {2} -Y_ {3} - Y_ {4} -Y_ {5} -Y_ {6} + Y_ {7} + Y_ {8}} {8}}. \\ [5pt] {\ widehat {\ theta}} _ {4} = { \ frac {Y_ {1} -Y_ {2} + Y_ {3} -Y_ {4} + Y_ {5} -Y_ {6} + Y_ {7} -Y_ {8}} {8}}. \\ [5pt] {\ widehat {\ theta}} _ {5} = {\ frac {Y_ {1} -Y_ {2} + Y_ {3} -Y_ {4} -Y_ {5} + Y_ {6} -Y_ {7} + Y_ {8}} {8}}. \\ [5pt] {\ widehat {\ theta}} _ {6} = {\ fra c {Y_ {1} -Y_ {2} -Y_ {3} + Y_ {4} + Y_ {5} -Y_ {6} -Y_ {7} + Y_ {8}} {8}}. \\ [ 5pt] {\ widehat {\ theta}} _ {7} = {\ frac {Y_ {1} -Y_ {2} -Y_ {3} + Y_ {4} -Y_ {5} + Y_ {6} + Y_ {7} -Y_ {8}} {8}}. \\ [5pt] {\ widehat {\ theta}} _ {8} = {\ frac {Y_ {1} + Y_ {2} + Y_ { 3} + Y_ {4} + Y_ {5} + Y_ {6} + Y_ {7} + Y_ {8}} {8}}. \ End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b6970abd1a6e69f062cddd667a1ea60088e94c8)
Вопрос планирования экспериментов: какой эксперимент лучше?
Дисперсия оценки X 1 для θ 1 равна σ, если мы используем первый эксперимент. Но если мы воспользуемся вторым экспериментом, то дисперсия приведенной выше оценки составит σ / 8. Таким образом, второй эксперимент дает нам в 8 раз большую точность для оценки одного элемента и оценивает все элементы одновременно с той же точностью. То, что достигается во втором эксперименте с восемью, потребует 64 взвешивания, если предметы взвешиваются отдельно. Однако обратите внимание, что оценки для пунктов, полученные во втором эксперименте, имеют ошибки, которые коррелируют друг с другом.
Многие проблемы планирования экспериментов связаны с комбинаторными планами, как в этом примере и других.
Ложноположительных заключений, часто в результате давления на публикацию или собственной предвзятости подтверждения автора, являются неотъемлемой опасностью во многих областях. Хороший способ предотвратить систематические ошибки, потенциально ведущие к ложным срабатываниям на этапе сбора данных, - это использовать двойной слепой дизайн. Когда используется двойной слепой дизайн, участники случайным образом распределяются по экспериментальным группам, но исследователь не знает, какие участники к какой группе принадлежат. Следовательно, исследователь не может повлиять на реакцию участников на вмешательство. Проблемой являются экспериментальные конструкции с нераскрытыми степенями свободы. Это может привести к сознательному или бессознательному «p-hacking »: пробовать несколько вещей до тех пор, пока вы не получите желаемый результат. Обычно это связано с манипулированием - возможно, бессознательным - процессом статистического анализа и степенями свободы до тех пор, пока они не вернут число ниже p <.05 level of statistical significance. So the design of the experiment should include a clear statement proposing the analyses to be undertaken. P-hacking can be prevented by preregistering researches, in which researchers have to send their data analysis plan to the journal they wish to publish their paper in before they even start their data collection, so no data manipulation is possible (https://osf.io ). Еще один способ предотвратить это - применить двойной слепой дизайн к фазе анализа данных, когда данные отправляются аналитику данных, не имеющему отношения к исследованию, который собирает данные, так что нет никакого способа узнать, к каким участникам относятся раньше. они потенциально могут быть исключены как выбросы.
Ясная и полная документация экспериментальной методологии также важна для поддержки воспроизведения результатов.
Экспериментальный план или рандомизированный Клиническое испытание требует тщательного рассмотрения нескольких факторов, прежде чем фактически проводить эксперимент. План эксперимента - это разработка подробного плана эксперимента перед проведением эксперимента. Некоторые из следующих тем уже обсуждались в разделе принципов экспериментального дизайна:
Независимая переменная исследования часто имеет много уровней или разных групп. В настоящем эксперименте исследователи могут иметь экспериментальную группу, в которой реализуется их вмешательство, проверяющее гипотезу, и контрольную группу, которая имеет тот же элемент, что и экспериментальная группа, без элемента вмешательства. Таким образом, когда все остальное, кроме одного вмешательства, остается неизменным, исследователи могут с некоторой уверенностью подтвердить, что именно этот элемент вызвал наблюдаемое изменение. В некоторых случаях наличие контрольной группы неэтично. Иногда это решается с помощью двух разных экспериментальных групп. В некоторых случаях независимыми переменными нельзя манипулировать, например, при тестировании разницы между двумя группами, у которых разное заболевание, или тестировании разницы между полами (очевидно, переменные, к которым было бы трудно или неэтично назначать участников). В этих случаях может использоваться квазиэкспериментальный план.
В чисто экспериментальном дизайне независимой (предикторной) переменной манипулирует исследователь, то есть каждый участник исследования выбирается случайным образом из совокупности, и каждый участник выбранный случайным образом назначается условиям независимой переменной. Только когда это будет сделано, можно с высокой вероятностью подтвердить, что причина различий в переменных результата вызвана различными условиями. Следовательно, исследователи должны по возможности выбирать экспериментальный план по сравнению с другими типами дизайна. Однако природа независимой переменной не всегда допускает манипуляции. В таких случаях исследователи должны знать, что нельзя сертифицировать причинно-следственную связь, если их дизайн не позволяет этого. Например, в планах наблюдения участники не распределяются по условиям случайным образом, и поэтому, если есть различия, обнаруженные в переменных результата между условиями, вполне вероятно, что есть нечто иное, чем различия между условиями, которые вызывают различия в результатах, что is - третья переменная. То же самое и с исследованиями с корреляционным дизайном. (Адер и Мелленберг, 2008 г.).
Лучше всего, чтобы процесс находился под разумным статистическим контролем до проведения запланированных экспериментов. Когда это невозможно, правильная блокировка, репликация и рандомизация позволяют тщательно проводить запланированные эксперименты. Чтобы контролировать мешающие переменные, исследователи вводят контрольные проверки в качестве дополнительных мер. Исследователи должны убедиться, что неконтролируемые влияния (например, восприятие достоверности источника) не искажают результаты исследования. Проверка манипуляции является одним из примеров контрольной проверки. Проверки манипуляции позволяют исследователям изолировать главные переменные, чтобы усилить поддержку того, что эти переменные работают, как планировалось.
Одним из наиболее важных требований к плану экспериментального исследования является необходимость устранения эффектов ложных, промежуточных и предшествующих переменных. В самой базовой модели причина (X) ведет к следствию (Y). Но может существовать третья переменная (Z), которая влияет на (Y), а X может быть вовсе не истинной причиной. Z считается ложной переменной, и ее необходимо контролировать. То же самое верно для промежуточных переменных (переменная между предполагаемой причиной (X) и следствием (Y)) и предшествующих переменных (переменная до предполагаемой причины (X), которая является истинной причина). Когда третья переменная задействована и не контролируется, отношение называется отношением. В большинстве практических применений планов экспериментальных исследований существует несколько причин (X1, X2, X3). В большинстве проектов одновременно обрабатывается только одна из этих причин.
Некоторые эффективные планы для оценки нескольких основных эффектов были найдены независимо и почти последовательно Раджем Чандрой Бозом и К. Кишеном в 1940 году в Индийский статистический институт, но оставался малоизвестным до тех пор, пока планы Плакетта-Бермана не были опубликованы в Biometrika в 1946 году. Примерно в то же время С. Р. Рао представил концепции ортогональных массивов как экспериментальные конструкции. Эта концепция сыграла центральную роль в разработке методов Тагучи Геничи Тагучи, которая имела место во время его визита в Индийский статистический институт в начале 1950-х годов. Его методы были успешно применены и приняты промышленными предприятиями Японии и Индии, а затем, хотя и с некоторыми оговорками, также были приняты промышленностью США.
В 1950 году Гертруда Мэри Кокс и Уильям Геммелл Кокран опубликовали книгу Experimental Designs, которая на долгие годы стала основным справочником по планированию экспериментов для статистиков..
Развитие теории линейных моделей охватило и превзошло случаи, которые касались ранних писателей. Сегодня теория опирается на сложные темы в линейной алгебре, алгебре и комбинаторике.
Как и в других отраслях статистики, экспериментальный план проводится с использованием как частотного и Байесовские подходы: при оценке статистических процедур, таких как экспериментальные планы, частотная статистика изучает распределение выборки, а байесовская статистика обновляет распределение вероятностей в пространстве параметров.
Некоторые важные участники в области экспериментального дизайна: C. С. Пирс, Р. А. Фишер, Ф. Йейтс, Р. К. Боз, А.С. Аткинсон, Р. А. Бейли, Д. Р. Кокс, Г. E. P. Box, W. Г. Кокран, В. Т. Федерер, В. В. Федоров, А. С. Хедаят, Дж. Кифер, О. Кемпторн, Дж. А. Нельдер, Андрей Пазман, Фридрих Пукельсхайм, Д. Рагхаварао, К. Р. Рао, Шриханд С. С., Дж. Н. Шривастава, Уильям Дж. Студден, Г. Тагучи и Х. П. Винн.
Учебники Д. Монтгомери, Р. Майерса и Г. Бокса / У. Хантер / Дж. Хантер достигли поколения студентов и практиков.
Некоторое обсуждение экспериментального дизайна в контексте идентификации системы (построение модели для статических или динамических моделей) приведено в и
Законы и этические соображения исключают некоторые тщательно спланированные эксперименты с людьми. Юридические ограничения зависят от юрисдикции. Ограничения могут включать экспертные советы учреждений, информированное согласие и конфиденциальность, влияющие как на клинические (медицинские) испытания, так и на поведенческие и социальные исследования. В области токсикологии, например, проводятся эксперименты на лабораторных животных с целью определения безопасных пределов воздействия для человека. Уравновешивание ограничений - взгляды из области медицины. Что касается рандомизации пациентов, «... если никто не знает, какая терапия лучше, нет этического императива использовать ту или иную терапию». (стр. 380) Что касается дизайна эксперимента, «... явно неэтично подвергать субъектов риску для сбора данных в плохо спланированном исследовании, когда этой ситуации можно легко избежать...». (стр. 393)
| На Wikimedia Commons есть материалы, связанные с разделом. |