В геометрии, A параллелепипед является трехмерный фигурой, образованной шесть параллелограммов (термин ромбовидный также иногда используются в этом значении). По аналогии он относится к параллелограмму так же, как куб относится к квадрату. В евклидовой геометрии четыре понятия - параллелепипед и куб в трех измерениях, параллелограмм и квадрат в двух измерениях - определены, но в контексте более общей аффинной геометрии, в которой углы не дифференцируются, существуют только параллелограммы и параллелепипеды. Три эквивалентных определения параллелепипеда:
- многогранник с шестью гранями ( шестигранники ), каждая из которых представляет собой параллелограмм,
- шестигранник с тремя парами параллельных граней, и
- призмы из которых основание представляет собой параллелограмм.
Прямоугольный кубоид (шесть прямоугольных граней), куб (шесть квадратных граней) и ромбоэдр (шесть граней ромба ) - все это частные случаи параллелепипеда.
"Параллелепипед" теперь обычно произносится / ° р Aer ə л ɛ л ɪ р ɪ р ɛ д /, / ˌ р Aer ə л ɛ л ɪ р aɪ р ɛ д / или / - р ɪ д / ; Традиционно это было / ˌ р Aer ə л ɛ л ɛ р ɪ р ɛ д / PARR -ə-lel- ЕР -i-пед в соответствии с его этимологией в греческом παραλληλεπίπεδον параллелепипеде, тело « имеющие параллельные плоскости».
Параллелепипеды - это подкласс призматоидов.
СОДЕРЖАНИЕ
- 1 Недвижимость
- 2 Объем
- 3 Площадь поверхности
- 4 Особые случаи по симметрии
- 5 Идеальный параллелепипед
- 6 параллелотоп
- 7 Лексикография
- 8 См. Также
- 9 Примечания
- 10 Ссылки
- 11 Внешние ссылки
Характеристики
Любую из трех пар параллельных граней можно рассматривать как базовые плоскости призмы. У параллелепипеда три набора из четырех параллельных ребер; края в каждом наборе имеют одинаковую длину.
Параллелепипеды результат линейных преобразований одного куба (для невырожденных случаев: биективные линейные преобразования).
Поскольку каждая грань имеет точечную симметрию, параллелепипед является зоноэдром. Также весь параллелепипед имеет точечную симметрию C i (см. Также триклиническую ). Каждое лицо, если смотреть снаружи, является зеркальным отражением противоположного лица. Грани в целом хиральные, а параллелепипед - нет.
Пространство заполнения тесселяции возможно при сравнимых копий любого параллелепипеда.
Объем

Параллелепипед, порожденный тремя векторами
Параллелепипед можно рассматривать как наклонную призму с параллелограммом в качестве основания. Следовательно, объем параллелепипеда - это произведение площади основания и высоты (см. Диаграмму). С участием 


-
 (где - угол между векторами и), и
(где - угол между векторами и), и


-
 (где угол между вектором и нормалью к основанию), получаем:
(где угол между вектором и нормалью к основанию), получаем:


Смешанное произведение трех векторов называется тройным произведением. Это можно описать определителем. Следовательно, объем: 
- (V1).

Другой способ доказать (V1) - использовать скалярную составляющую в направлении вектора: Результат следует. 


Альтернативное представление объема использует только геометрические свойства (углы и длины кромок):
- (V2),

где и - длины ребер. 

- Доказательство (V2)
Доказательство (V2) использует свойства определителя и геометрическую интерпретацию скалярного произведения :
Позвольте быть 3x3-матрицей, столбцы которой - векторы (см. Выше). Тогда верно следующее: 



- (расширение определителя выше по первой строке)








(Используйте последние шаги) 
- Соответствующий тетраэдр
Объем любого тетраэдра, который имеет три сходящихся ребра параллелепипеда, равен одной шестой объема этого параллелепипеда (см. Доказательство ).
Площадь поверхности
Площадь поверхности параллелепипеда складывается из площадей ограничивающих параллелограммов:
-

-
 .
.
(Для маркировки: см. Предыдущий раздел.)
Особые случаи по симметрии
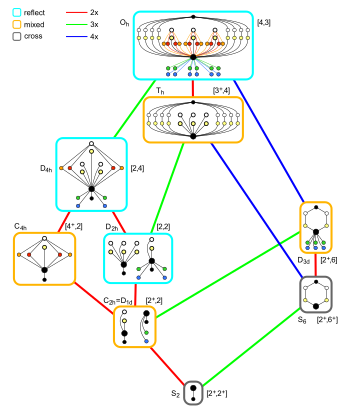 Отношения подгруппы октаэдрической симметрии с центром инверсии Отношения подгруппы октаэдрической симметрии с центром инверсии | 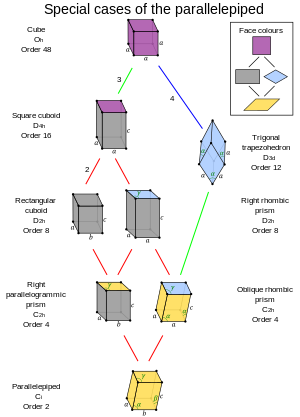 Частные случаи параллелепипеда Частные случаи параллелепипеда |
| Форма | Куб | Квадратный кубоид | Тригональный трапецоэдр | Прямоугольный кубоид | Правая ромбическая призма | Правая параллелограммная призма | Косая ромбическая призма |
| Ограничения |   |   |   |  |   |  |   |
| Симметрия | О ч порядка 48 | D 4ч порядка 16 | D 3d заказ 12 | D 2h порядка 8 | C 2h порядка 4 |
| Изображение |  |  |  |  |  |  |  |
| Лица | 6 квадратов | 2 квадрата, 4 прямоугольника | 6 ромбов | 6 прямоугольников | 4 прямоугольника, 2 ромба | 4 прямоугольника, 2 параллелограмма | 2 ромба, 4 параллелограмма |
- Параллелепипед с симметрией O h известен как куб, имеющий шесть одинаковых квадратных граней.
- Параллелепипед с симметрией D 4h известен как квадратный кубоид, у которого есть две квадратные грани и четыре совпадающие прямоугольные грани.
- Параллелепипед с симметрией D 3d известен как тригональный трапецоэдр, который имеет шесть конгруэнтных ромбических граней (также называемых изоэдральным ромбоэдром).
- Для параллелепипедов с симметрией D 2h возможны два случая:
- Прямоугольный кубоид : у него шесть прямоугольных граней (также называемых прямоугольным параллелепипедом или иногда просто кубоидом).
- Правая ромбическая призма: у нее две ромбические грани и четыре конгруэнтных прямоугольных грани.
- Примечание: частный случай полностью ромбической формы с двумя ромбическими гранями и четырьмя конгруэнтными квадратными гранями имеет то же имя и одну и ту же группу симметрии (D 2h, порядок 8).

- Для параллелепипедов с симметрией C 2h возможны два случая:
- Правая параллелограммная призма: у нее четыре прямоугольные грани и две параллелограммные грани.
- Косая ромбическая призма: у нее две ромбические грани, а из остальных граней две соседние равны, а две другие тоже (две пары являются зеркальным отображением друг друга).
Идеальный параллелепипед
Идеально параллелепипед представляет собой параллелепипед с целым числом длиной ребер, гранями диагоналями и пространственными диагоналями. В 2009 году было показано, что существуют десятки идеальных параллелепипедов, что явилось ответом на открытый вопрос Ричарда Гая. Один пример имеет края 271, 106 и 103, второстепенные диагонали 101, 266 и 255 грани, большие диагонали лица 183, 312 и 323 и диагонали пространства 374, 300, 278 и 272.
Известны идеальные параллелепипеды с двумя прямоугольными гранями. Но неизвестно, существуют ли такие, у которых все грани прямоугольные; такой случай можно было бы назвать идеальным кубоидом.
Параллелотоп
Коксетер назвал обобщение параллелепипеда в более высоких измерениях параллелоэдром. В современной литературе выражение параллелепипед также часто используется в более высоких (или произвольных конечных) измерениях.
В частности, в n -мерном пространстве он называется n -мерным параллелогранником или просто n -параллелепипедом (или n- параллелепипедом). Таким образом, параллелограмм - это 2-параллелоэдр, а параллелепипед - это 3-параллелоэдр.
В более общем смысле параллелоэдр или параллелоэдр Вороного имеет параллельные и совпадающие противоположные грани. Итак, 2-параллелоэдр - это параллелогон, который также может включать в себя определенные шестиугольники, а 3-параллелоэдр - это параллелоэдр, включающий 5 типов многогранников.
В диагоналями из в п -parallelotope пересекаются в одной точке и делятся пополам этим пунктом. При инверсии в этой точке n -параллелэдр остается неизменным. См. Также неподвижные точки групп изометрий в евклидовом пространстве.
Ребра, исходящие из одной вершины k -параллелоэдра, образуют k- каркас векторного пространства, и параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1. 
П -VOLUME из п -parallelotope встроенное в котором может быть вычислено с помощью определителя Грама. В качестве альтернативы объем - это норма внешнего произведения векторов: 


Если m = n, это составляет абсолютное значение определителя n векторов.
Еще одна формула для вычисления объема с п -parallelotope Р в, которого п + 1 вершины, является 

![{\ Displaystyle {\ rm {Vol}} (P) = | {\ rm {det}} \ ([V_ {0} \ 1] ^ {\ rm {T}}, [V_ {1} \ 1] ^ {\ rm {T}}, \ ldots, [V_ {n} \ 1] ^ {\ rm {T}}) |,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06a470275bbaf5ff23b98e44c462836f5a5eb71d)
где - вектор-строка, образованный конкатенацией и 1. Действительно, определитель не изменяется, если вычитается из ( i gt; 0), а размещение в последней позиции меняет только его знак. ![{\ displaystyle [V_ {i} \ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2362bea0baa876bb7e76e2c43bbac55d2241798)

![{\ displaystyle [V_ {0} \ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fe4ab89b67a521fcf8097b1a2996fdda40fba1e)
![{\ displaystyle [V_ {i} \ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2362bea0baa876bb7e76e2c43bbac55d2241798)
![{\ displaystyle [V_ {0} \ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fe4ab89b67a521fcf8097b1a2996fdda40fba1e)
Кроме того, объем любого п - симплекс, который разделяет п сходящиеся ребра параллелепипеда имеет объем, равный единице 1 / п ! объема этого параллелоэдра.
Лексикография
Слово появляется как parallelipipedon в переводе сэра Генри Биллингсли « Элементов» Евклида, датированного 1570 годом. В издании своего Cursus mathematicus 1644 года Пьер Эригон использовал правописание « параллелепипед». В Оксфордском словаре английского языка современный параллелепипед впервые появился в « Chorea gigantum» Уолтера Чарлтона (1663).
Словарь Чарльза Хаттона (1795) показывает параллелепипед и параллелепипед, демонстрируя влияние объединяющей формы параллело-, как если бы второй элемент был трубопроводом, а не эпипедоном. Ной Вебстер (1806) включает орфографический параллелепипед. Издание Оксфордского словаря английского языка 1989 года описывает параллелепипед (и параллелепипед) явно как неправильные формы, но они перечислены без комментариев в издании 2004 года, и даны только произношения с акцентом на пятый слог пи ( / paɪ /).
Отклонение от традиционного произношения скрыло различное разделение, предложенное греческими корнями, с epi- («он») и pedon («земля»), объединенными, чтобы дать epiped, плоскую «плоскость». Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.
Смотрите также
Примечания
использованная литература
- Кокстер, Регулярные многогранники HSM, 3-е изд. Нью-Йорк: Довер, стр. 122, 1973. (Он определяет параллелоэдр как обобщение параллелограмма и параллелепипеда в n-мерном пространстве.)
внешние ссылки

 Параллелепипед, порожденный тремя векторами
Параллелепипед, порожденный тремя векторами  Отношения подгруппы октаэдрической симметрии с центром инверсии
Отношения подгруппы октаэдрической симметрии с центром инверсии  Частные случаи параллелепипеда
Частные случаи параллелепипеда





