Тетрация

Повторное или повторяющееся возведение в степень

Раскраска домена голоморфной тетрации $ze\; \{\backslash \; displaystyle\; \{\}\; ^\; \{z\}\; e\}$, где оттенок представляет функцию аргумент, а яркость представляет собой $nx\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; x\}$, для n = 2, 3, 4,..., показывающий сходимость к бесконечно повторяющейся экспоненте между двумя точками

В математике, тетрация (или гипер-4 ) - это операция, основанная на итерации, или повторяющейся возведении в степени. Это следующая гипероперация после возведения в степень, но перед возведением в степень. Слово было придумано Рубеном Луи Гудстейном из тетра- () и итерация.

Под определением как повторное возведение в степень, обозначение $na\; \{\backslash \; displaystyle\; \{^\; \{n\}\; a\}\}$означает $aa\; \cdot \; \cdot \; a\; \{\backslash \; displaystyle\; \{a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\}\}\}\}\}\}$, где n копий повторяются посредством возведения в степень справа налево, т.е. применение возведения в степень $n\; -\; 1\; \{\backslash \; displaystyle\; n-1\}$раз. n называется «высотой» функции, а называется «основанием», аналогично возведению в степень. Это будет читаться как «энное тетрирование а».

Тетрация также определяется рекурсивно как

$na:\; =\; \{1\; if\; n\; =\; 0\; a\; ((n\; -\; 1)\; a)\; if\; n>0\; \{\backslash \; displaystyle\; \{^\; \{n\}\; a\}:\; =\; \{\backslash \; begin\; \{case\}\; 1\; \{\backslash \; text\; \{if\}\}\; n\; =\; 0\; \backslash \backslash \; a\; ^\; \{\backslash \; left\; (^\; \{(n-1)\}\; a\; \backslash \; right)\}\; \{\backslash \; text\; \{if\}\}\; n>0\; \backslash \; end\; \{case\}\}\}$,

, позволяющий расширить тетрацию до не натуральных чисел, таких как действительные и комплексные числа.

Две инверсии тетрации называются супер-корень суперлогарифм, аналогичные корню n-й степени и логарифмическими функциями. Ни одна из трех функций не является элементом арной.

Тетрацией. запись очень больших чисел.

• 1 Введение
• 2 Терминология
• 3 Обозначение
• 4 Примеры
• 5 Свойства
  • 5.1 Направление оценки
• 6 Расширения
  • 6.1 Расширение домена для баз
    • 6.1. 1 Базовый н оль
    • 6.1.2 Завершено x баз
  • 6.2 Расширения области для разных высот
    • 6.2.1 Бесконечные высоты
    • 6.2.2 Отрицательные высоты
    • 6.2.3 Реальные высоты
      • 6.2.3.1 Линейное 6.2.3.2 Аппроксимации высших порядков для реального высот
    • 6.2.4 Комплексные высоты
• 7 Неэлементарная рекурсивность
• 8 Обратные операции
  • 8.1 Суперкорень
    • 8.1.1 Квадратный суперкорень
    • 8.1.2 Другие суперкорни
  • 8.2 Суперлогарифм
• 9 Открытые вопросы
• 10 См. Также
• 11 Примечания
• 12 Ссылки
• 13 Дополнительная литература

Здесь показаны первые четыре гипероперации этого, при тетрация считается четвертой в серии. унарная операция последовательность, определенная как $a\; \text{'}=\; a\; +\; 1\; \{\backslash \; displaystyle\; a\text{'}\; =\; a\; +\; 1\}$, считается нулевая операция.

1. Сложение

   $a\; +\; n\; =\; a\; +\; 1\; +\; 1\; +\; \cdots \; +\; 1\; ⏟\; n\; \{\backslash \; displaystyle\; a\; +\; n\; =\; a\; +\; \backslash \; underbrace\; \{1\; +\; 1\; +\; \backslash \; cdots\; +1\}\; \_\; \{n\}\}$

   копий 1, добавленных к a.

2. Умножение

   $a\; \times \; n\; =\; a\; +\; a\; +\; \cdots \; +\; a\; ⏟\; n\; \{\backslash \; displaystyle\; a\; \backslash \; times\; n\; =\; \backslash \; underbrace\; \{a\; +\; a\; +\; \backslash \; cdots\; +\; a\}\; \_\; \{n\}\}$

   n копий сложения.

3. Возведение в степень

   $an\; =\; a\; \times \; a\; \times \; \cdots \; \times \; a\; ⏟\; n\; \{\backslash \; displaystyle\; a\; ^\; \{n\}\; =\; \backslash \; underbrace\; \{a\; \backslash \; times\; a\; \backslash \; times\; \backslash \; cdots\; \backslash \; times\; a\}\; \_\; \{n\}\}$

   копий а, объединенных умножением.

4. Тетрация

   $na\; =\; aa\; \cdot \; \cdot \; a\; ⏟\; n\; \{\backslash \; displaystyle\; \{^\; \{n\}\; a\}\; =\; \backslash \; underbrace\; \{a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\}\}\}\}\}\}\; \_\; \{n\}\}$

   копий, объединенных возведением в степень справа налево.

Последовательность, (a ′ = a + 1) - самая простая операция; в то время как сложение (a + n) является основной операцией, для сложения натуральных чисел его можно рассматривать как последовательность последовательных последователей a; Умножение (a × n) также является основной операцией, хотя для натуральных чисел его можно рассматривать как сложение цепочки, включающее n чисел от a. Возведение в степень можно представить как цепное умножение, включающее n чисел a, и тетрацию ($n\; a\; \{\backslash \; displaystyle\; ^\; \{n\}\; a\; \backslash !\}$) как связанную степень, включающую n чисел a. Каждая из вышеперечисленных операций определяется повторением предыдущей; однако в отличие от предшествующих операций, тетрация не является основной функцией .

Параметр включается как base, а параметр n может называться height . В исходном определении тетрации параметр высоты должен быть натуральным числом; например, было бы нелогично сказать, что «три подняли к себе отрицание пять раз» или «подняли к себе половину времени». Так же, как сложение, умножение и возведение в степень могут быть использованы возможности расширять действительные и комплексные числа, было предпринято несколько попыток обобщить тетрацию на отрицательные числа, действительные числа и комплексные числа. Один из таких способов - использовать рекурсивное определение тетрации; для любого положительного значения real $a>0\; \{\backslash \; displaystyle\; a>0\}$и неотрицательный integer $n\; \ge \; 0\; \{\backslash \; displaystyle\; n\; \backslash \; geq\; 0\}>$, мы можем определить $na\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \{^\; \{N\}\; a\}\}$рекурсивно как:

$na:\; =\; \{1\; if\; n\; =\; 0\; a\; ((n\; -\; 1)\; а)\; если\; n>0\; \{\backslash \; displaystyle\; \{^\; \{n\}\; a\}:\; =\; \{\backslash \; begin\; \{cases\}\; 1\; \{\backslash \; text\; \{if\}\}\; n\; =\; 0\; \backslash \backslash \; a\; ^\; \{\backslash \; left\; (^\; \{(n\; -\; 1)\}\; a\; \backslash \; right)\}\; \{\backslash \; text\; \{if\}\}\; n>0\; \backslash \; end\; \{cases\}\}\}$

Рекурсивное естественное определение эквивалентного повторного определения в степени <для <2 возмещения>64327; однако это допускает расширение на другие высоты, такие как $0\; a\; \{\backslash \; displaystyle\; ^\; \{0\}\; a\}$, $-\; 1\; a\; \{\backslash \; displaystyle\; ^\; \{-\; 1\}\; a\}$, а также $ia\; \{\backslash \; displaystyle\; ^\; \{i\}\; a\}$- многие из этих расширений являются областями активных исследований.

существует множество терминов для обозначения обозначения тетрации, каждый из которых имеет определенную логику, но некоторые из них не стали широко использоваться той или иной причине. Вот сравнение каждого термина с его обоснованием и контробоснованием.

• Термин тетрация, введенный Гудштейном в его статье 1947 года «Трансфинитные порядки в рекурсивной теории чисел» (обобщение рекурсивного базового представления, используемого в теореме Гудстейна для использования более высоких операций), стало доминирующим. Он также был популяризирован в книге Руди Ракера Бесконечность и разум.
• . Термин сверхэкспоненциация был опубликован Бромером в его статье «Суперэкспоненциация» в 1987 году. Ранее его использовал Эд Нельсон в своей книге «Предикатив». Арифметика, Princeton University Press, 1986.
• Термин гиперсила - это естественная комбинация гиперсилы и мощности, которая точно эта тетрация. Проблема заключается в значении гипероперации по отношению к последовательности гипероперации. При рассмотрении гиперопераций термин гипер относится ко всем рангам, а термин супер относится к рангу 4 или тетрации. Таким образом, в соответствии с этими соображениями гиперсила вводит в заблуждение, поскольку относится только к тетрации.
• Термин «силовая башня порядка n» иногда используется в форме силовая установка порядка n »для $aa\; \cdot \; \cdot \; a\; ⏟\; n\; \{\backslash \; displaystyle\; \{\backslash \; \backslash \; atop\; \{\backslash \}\}\; \{\{\backslash \; underbrace\; \{a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\}\}\}\}\}\}\; \backslash \; atop\; n\}\}$. Однако это неправильное название, потому что тетрация может быть выражена с помощью повторяющихся степенных функций (см. Выше), поскольку это итерационная экспоненциальная функция.

Отчасти из-за некоторой общей терминологии и аналогичной нотации, часто путают со связанными функциями и выражениями. Вот несколько связанных терминов:

Термины, относящиеся к тетрации

Терминология	Форма
Тетрация	$aa\; \cdot \; \cdot \; aa\; \{\backslash \; displaystyle\; a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\; ^\; \{a\}\}\}\}\}\}$
Итерированные экспоненты	$aa\; \cdot \; \cdot \; ax\; \{\backslash \; displaystyle\; a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\; ^\; \{x\}\}\}\}\}\}\; \}\}$
Вложенные экспоненты (также башни)	$a\; 1\; a\; 2\; \cdot \; \cdot \; an\; \{\backslash \; displaystyle\; a\_\; \{1\}\; ^\; \{a\_\; \{2\}\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\_\; \{n\}\}\}\; \}\}\}$
Бесконечные экспоненты (также башни)	$a\; 1\; a\; 2\; a\; 3\; \cdot \; \cdot \; \cdot \; \{\backslash \; displaystyle\; a\_\; \{1\}\; ^\; \{a\_\; \{2\}\; ^\; \{a\_\; \{3\}\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\}\}\}\}\}\}$

Первые выражения a - это основание, количество появлений - это высота (дополнительная единицу для x). В третьем выражении n - высота, но каждое из оснований отличается.

Следует проявлять осторожность при обращении к повторяющимся экспонентам, так как выражения этой формы обычно называют повторным возведением в степени, что неоднозначно, так как это может означать либо итерированные степени или повторяющиеся экспоненты.

Существует много разных стилей обозначений, которые можно использовать для выражения тетрации. Некоторые из них ограничиваются распространением других моделей ..

Стили обозначения для тетрации

Имя	Форма	Описание
Обозначение Руди Ракера	$na\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{n\}\; a\}$	Используется Маурером [1901] и Гудстейном [1947]; Книга Руди Ракера Бесконечность и разум популяризировала обозначения.
Нотация Кнута со стрелкой вверх	$a\; \uparrow \uparrow \; n\; \{\backslash \; displaystyle\; a\; \{\backslash \; uparrow\; \backslash \; uparrow\}\; n\}$	Разрешает расширение, добавляя больше стрелок или, что еще более важно, индексированную стрелку.
Цепная стрелка Конвея	$a\; \to \; n\; \to \; 2\; \{\backslash \; displaystyle\; a\; \backslash \; rightarrow\; n\; \backslash \; rightarrow\; 2\}$	Позволяет расширить за счет увеличения числа 2 (эквивалентно указанным выше расширениям), но также еще более мощно, продолжая цепочку
функция Аккермана	$n\; 2\; =\; A\; \; (4,\; n\; -\; 3)\; +\; 3\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; 2\; =\; \backslash \; operatorname\; \{A\}\; (4,\; n-3)\; +3\}$	Позволяет записать специальный случай $a\; =\; 2\; \{\backslash \; displaystyle\; a\; =\; 2\}$в терминах функции Аккермана.
Итерированная экспоненциальная запись	$exp\; an\; \; (1)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{a\}\; ^\; \{n\}\; (1)\}$	Позволяет простое расширение до повторяющихся экспонентов от начальных значений, отличных от 1.
Обозначения Хушмана	$uxp\; a\; \; nan\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{uxp\}\; \_\; \{a\}\; n\; \backslash \backslash \; [2pt]\; a\; ^\; \{\backslash \; frac\; \{n\}\; \{\}\}\; \backslash \; end\; \{выровнено\}\}\}$	Используется MH Hooshmand [2006].
Гипероперация нотации	$a\; [4]\; n\; H\; 4\; (a,\; n)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; a\; [4]\; n\; \backslash \backslash \; [2pt]\; H\_\; \{4\}\; (a,\; n)\; \backslash \; end\; \{align\}\}\}$	Разрешает расширение путем увеличения числа 4; это дает семейство гиперопераций.
Обозначение двойной вставки	a ^^ n	Так как стрелка вверх идентично используется вставке (^), может быть записано тетратирование как (^ ^); удобно для ASCII.

В одном из приведенных выше обозначений используется итеративная экспоненциальная запись; в общем это определяется следующим образом:

$exp\; an\; \; (x)\; =\; aa\; \cdot \; \cdot \; ax\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{a\}\; ^\; \{n\}\; (x)\; =\; a\; ^\; \{a\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{a\; ^\; \{x\}\}\}\}\}\}$с n как.

Существует не так много обозначений для повторяющихся экспонентов, но вот несколько:

Стили обозначений для повторяющихся экспонент

Имя	Форма	Описание
Стандартное обозначение	$exp\; an\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{a\}\; ^\; \{n\}\; (x)\}$	Эйлер ввел обозначение $exp\; a\; \; (x)\; =\; ax\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{\; a\}\; (x)\; =\; a\; ^\; \{x\}\}$и обозначение итераций $fn\; (x)\; \{\backslash \; displaystyle\; f\; ^\; \{n\}\; (x)\}$существует примерно столько же.
Обозначение Ключ со стрелкой вверх	$(a\; \uparrow )\; n\; (x)\; \{\backslash \; displaystyle\; (a\; \{\backslash \; uparrow\})\; ^\; \{n\}\; (x)\}$	Позволяет использовать сверхдержавы и суперэкспоненциальную функцию за счет увеличения количества стрелок; используется в статье о больших чисел.
Текстовое обозначение	exp_a ^ n (x)	На основе стандартных обозначений; удобно для ASCII.
J Notation	x ^^ :( n-1) x	Повторяет возведение в степень. См. J (язык программирования)

Из-за быстрого роста большого числа показателей в следующей таблице слишком велики записи в экспоненциальной нотации. В этих случаях используется итеративная экспоненциальная запись, чтобы выразить их в базе 10. Значения, десятичная точка приблизительной.

Примеры тетрации

$x\; \{\backslash \; displaystyle\; x\}$	$2\; x\; \{\backslash \; displaystyle\; \{\}\; ^\; \{2\}\; x\}$	$3\; x\; \{\backslash \; displaystyle\; \{\}\; ^\; \{3\}\; x\}$	$4\; x\; \{\backslash \; displaystyle\; \{\}\; ^\; \{4\}\; x\}$	$5\; x\; \{\backslash \; displaystyle\; \{\}\; ^\; \{5\}\; x\}$
1	1	1	1	1
2	4	16	65,536	2 или (2,00353 × 10)
3	27	7 625 597 484 987	$exp\; 10\; 3\; \; (1.09902)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (1.09902)\}$(3,6 × 10 цифр)	$ехр\; 10\; 4\; \; (1,09902)\; \{\backslash \; Displaystyle\; \backslash \; ехр\; \_\; \{10\}\; ^\; \{4\}\; (1,09902)\}$
4	256	1,34078 × 10	$ехр\; 10\; 3\; \; (2,18726)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (2,18726)\}$(8,1 × 10 цифр)	$exp\; 10\; 4\; \; (2,18726)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (2,18726)\}$
5	3,125	1,91101 × 10	$exp\; 10\; 3\; \; (3,\; 33928)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (3.33928)\}$(1,3 × 10 цифр)	$exp\; 10\; 4\; \; (3.33928)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (3.33928)\}$
6	46 656	2 65912 × 10	$exp\; 10\; 3\; \; (4.55997)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (\; 4.55997)\}$(2,1 × 10 цифр)	$exp\; 10\; 4\; \; (4.55997)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (4.55997)\}$
7	823 543	3.75982 × 10	$exp\; 10\; 3\; \; (5.84259)\; \{\backslash \; displaystyle\; \backslash \; ехр\; \_\; \{10\}\; ^\; \{3\}\; (5,84259)\}$(3,2 × 10 цифр)	$ехр\; 10\; 4\; \; (5,84259)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{\; 4\}\; (5,84259)\}$
8	16,777,216	6,01452 × 10	$exp\; 10\; 3\; \; (7.18045)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (7.18045)\}$(5,4 × 10 цифр)	$exp\; 10\; 4\; \; (7.18045)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (7.18045)\}$
9	387 420 489	4,28125 × 10	$exp\; 10\; 3\; \; (8,56784)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (8.56784)\}$(4,1 × 10 цифр)	$ехр\; 10\; 4\; \; (8.56784)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (8.56784)\}$
10	10,000,000,000	10	$exp\; 10\; 3\; \; (10)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{3\}\; (10)\}$(10 + 1 цифр)	$exp\; 10\; 4\; \; (10)\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{10\}\; ^\; \{4\}\; (\; 10)\}$

У тетрации есть несколько свойств, похожих на возведение в степень, а также свойства, которые специфические для операции и теряются или получаются в результате возведения в степень. Возведение в степень не коммутирует, правила произведения и степени не имеют аналога с тетрацией; выражения $a\; (bx)\; =\; (abx)\; \{\backslash \; textstyle\; \{\}\; ^\; \{a\}\; \backslash \; left\; (\{\}\; ^\; \{b\}\; x\; \backslash \; right)\; =\; \backslash \; left\; (\{\}\; ^\; \{ab\}\; x\; \backslash \; right)\}$и $a\; (xy)\; =\; axay\; \{\backslash \; textstyle\; \{\}\; ^\; \{a\}\; \backslash \; left\; (xy\; \backslash \; right)\; =\; \{\}\; ^\; \{a\}\; x\; \{\}\; ^\; \{a\}\; y\}$не обязательно верны для всех случаев.

Однако тетрация имеет другое свойство, в котором $ax\; =\; x\; (a\; -\; 1\; x)\; \{\backslash \; textstyle\; \{\}\; ^\; \{a\}\; x\; =\; x\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{a-1\; \}\; x\; \backslash \; right)\}\}$. Этот факт наиболее ярко проявляется в рекурсивном определении. Из свойств этого следует доказательство того, что $(ba)\; (ca)\; =\; (c\; +\; 1\; a)\; (b\; -\; 1\; a)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\}\; ^\; \{b\}\; a\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{c\}\; a\; \backslash \; right)\}\; =\; \backslash \; left\; (\{\}\; ^\; \{c\; +\; 1\}\; a\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{b-1\}\; a\; \backslash \; right)\}\}$, который позволяет переключать b и c в некоторых уравнениях. Доказательство выглядит следующим образом:

$(ba)\; (ca)\; =\; (ab\; -\; 1\; a)\; (ca)\; =\; a\; (b\; -\; 1\; a)\; (ca)\; =\; a\; (ca)\; (b\; -\; 1\; a)\; =\; (c\; +\; 1\; a)\; (b\; -\; 1\; a)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; left\; (\{\}\; ^\; \{b\}\; a\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{c\}\; a\; \backslash \; right)\}\; \backslash \; \backslash \; =\; \{\}\; \backslash \; left\; (a\; ^\; \{\{\}\; ^\; \{b-1\}\; a\}\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{c\}\; a\; \backslash \; right)\}\; \backslash \backslash \; =\; \{\}\; a\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{b-1\}\; a\; \backslash \; right)\; \backslash \; left\; (\{\}\; ^\; \{c\}\; a\; \backslash \; right)\}\; \backslash \backslash \; =\; \{\}\; a\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{c\}\; a\; \backslash \; right)\; \backslash \; left\; (\{\}\; ^\; \{b-1\}\; a\; \backslash \; right)\}\; \backslash \backslash \; =\; \{\}\; \backslash \; left\; (\{\}\; ^\; \{c\; +\; 1\}\; a\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{b-1\}\; a\; \backslash \; right)\}\; \backslash \; end\; \{align\}\}\}$

Когда числа x и 10 являются взаимно простыми, можно вычислить последние m десятичных цифр $ax\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \backslash \; ^\; \{a\}\; x\}$с использованием теоремы Эйлера для любого целого числа m.

Направление оценки

При оценке тетрации, выраженной как «башня возведения в степень», последовательное возведение в степень сначала выполняется на самом глубоком уровне (в обозначениях, на вершине). Например:

$4\; 2\; =\; 2\; 2\; 2\; 2\; =\; 2\; (2\; (2\; 2))\; =\; 2\; (2\; 4)\; =\; 2\; 16\; =\; 65,\; 536\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \backslash \; ^\; \{4\}\; 2\; =\; 2\; ^\; \{2\; ^\; \{2\; ^\; \{2\}\}\}\; =\; 2\; ^\; \{\backslash \; left\; (2\; ^\; \{\backslash \; left\; (2\; ^\; \{2\}\; \backslash \; right)\}\; \backslash \; right)\}\; =\; 2\; ^\; \{\; \backslash \; left\; (2\; ^\; \{4\}\; \backslash \; right)\}\; =\; 2\; ^\; \{16\}\; =\; 65,\; \backslash !\; 536\}$

Этот порядок важен, потому что возведение в степень не является ассоциативным, и выражение вычисляется в противоположном порядке приводит к другому ответу:

$2\; 2\; 2\; 2\; \ne \; (\; (2\; 2)\; 2)\; 2\; знак\; равно\; 4\; 2\; \cdot \; 2\; =\; 256\; \{\backslash \; Displaystyle\; \backslash ,\; \backslash !\; 2\; ^\; \{2\; ^\; \{2\; ^\; \{2\}\}\}\; \backslash \; neq\; \backslash \; left\; (\{\backslash \; left\; (2\; ^\; \{2\}\; \backslash \; right)\}\; ^\; \{2\}\; \backslash \; right)\; ^\; \{2\}\; =\; 4\; ^\; \{2\; \backslash \; cdot\; 2\; \}\; =\; 256\}$

Вычисление выражения слева до считается менее интересным; путем вычисления слева направо, выражение $na\; \{\backslash \; displaystyle\; ^\; \{n\}\; a\; \backslash !\}$можно упростить до $a\; (an\; -\; 1)\; \{\backslash \; displaystyle\; a\; ^\; \{\backslash \; left\; (a\; ^\; \{n-1\}\; \backslash \; right)\}\; \backslash !\; \backslash !\}$. Из-за этой башни нужно оценивать справа налево (или сверху вниз). Программисты называют этот выбор правоассоциативным.

Тетрация может быть расширена двумя способами; в уравнении $n\; a\; \{\backslash \; displaystyle\; ^\; \{n\}\; a\; \backslash !\}$как основание a, так и высота n могут быть получены с использованием определения и свойств тетрации. Хотя основание и высота могут быть расширены за пределы неотрицательных целых чисел на разные домены, включая $n\; 0\; \{\backslash \; displaystyle\; \{^\; \{n\}\; 0\}\}$, сложные такие функции, как $ni\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; i\}$, и высота бесконечного n, более ограниченные свойства тетрации уменьшают возможность расширения тетрации.

Расширение домена для баз

Базовый ноль

Экспонента $0\; 0\; \{\backslash \; displaystyle\; 0\; ^\; \{0\}\}$не всегда определено. Таким образом, тетрации $n\; 0\; \{\backslash \; displaystyle\; \backslash ,\; \{^\; \{n\}\; 0\}\}$четко не определенная формулой, приведенной ранее. Однако $lim\; x\; \to \; 0\; nx\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{x\; \backslash \; rightarrow\; 0\}\; \{\}\; ^\; \{n\}\; x\}$определен правильно и существует:

$lim\; x\; \to \; 0\; nx\; =\; \{\; 1,\; n\; четный\; 0,\; n\; нечетный\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{x\; \backslash \; rightarrow\; 0\}\; \{\}\; ^\; \{n\}\; x\; =\; \{\backslash \; begin\; \{cases\}\; 1,\; n\; \{\backslash \; text\; \{even\}\}\; \backslash \backslash \; 0,\; n\; \{\backslash \; text\; \{odd\}\}\; \backslash \; end\; \{cases\}\}\}$

Таким образом, мы можем определить определение $n\; 0\; =\; lim\; x\; \to \; 0\; nx\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; 0\; =\; \backslash \; lim\; \_\; \{x\; \backslash \; rightarrow\; 0\}\; \{\}\; ^\; \{n\}\; x\}$. Это аналогично определению $0\; 0\; =\; 1\; \{\backslash \; displaystyle\; 0\; ^\; \{0\}\; =\; 1\}$.

В рамках этого расширения $0\; 0\; =\; 1\; \{\backslash \; displaystyle\; \{\}\; ^\; \{0\}\; 0\; =\; 1\}$, поэтому правило $0\; a\; =\; 1\; \{\backslash \; displaystyle\; \{^\; \{0\}\; a\}\; =\; 1\}$из исходного определения все еще сохраняется.

Сложные основания

Тетрация по периоду Тетрация по периоду

Мах комплексные числа могут быть возведены в степени, тетрация может быть правил к базам формы z = a + bi ( где a и b действительны). Например, в z с z = i тетрация достигается за счет использования главной ветви натурального логарифма; используя формулу Эйлера, получаем соотношение:

$ia\; +\; bi\; =\; e\; 1\; 2\; \pi \; i\; (a\; +\; bi)\; =\; e\; -\; 1\; 2\; \pi \; b\; (cos\; \; \pi \; a\; 2\; +\; i\; sin\; \; \pi \; a\; 2)\; \{\backslash \; displaystyle\; i\; ^\; \{a\; +\; bi\}\; =\; e\; ^\; \{\{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; pi\; i\}\; (a\; +\; bi)\}\; =\; e\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\; \}\; \{\backslash \; pi\; b\}\}\; \backslash \; left\; (\backslash \; cos\; \{\backslash \; frac\; \{\backslash \; pi\; a\}\; \{2\}\}\; +\; i\; \backslash \; sin\; \{\backslash \; frac\; \{\backslash \; pi\; a\}\; \{2\}\}\; \backslash \; right)\}$

Это предполагает рекурсивное определение для i = a ′ + b′i для любого i = a + bi:

$a\; \prime \; =\; e\; -\; 1\; 2\; \pi \; b\; cos\; \; \pi \; a\; 2\; b\; \prime \; =\; e\; -\; 1\; 2\; \pi \; b\; sin\; \; \pi \; a\; 2\; \{\; \backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; a\; \text{'}=\; e\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; pi\; b\}\}\; \backslash \; cos\; \{\backslash \; frac\; \{\backslash \; pi\; a\}\; \{2\}\}\; \backslash \backslash \; [2pt\; ]\; b\; \text{'}=\; e\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; pi\; b\}\}\; \backslash \; sin\; \{\backslash \; frac\; \{\backslash \; pi\; a\}\; \{2\}\}\; \backslash \; end\; \{align\}\}\}$

Следующие приблизительные значения могут быть получены:

Значения тетрации сложных основ

$ni\; \{\backslash \; textstyle\; \{\}\; ^\; \{n\}\; i\}$	Приблизительное значение
$1\; i\; =\; i\; \{\backslash \; textstyle\; \{\}\; ^\; \{1\}\; i\; =\; i\}$	i
$2\; i\; =\; i\; (1\; i)\; \{\backslash \; textstyle\; \{\}\; ^\; \{2\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{1\}\; i\; \backslash \; right)\}\}$	0,2079
$3\; я\; =\; я\; (2\; я)\; \{\backslash \; тексты\; tyle\; \{\}\; ^\; \{3\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{2\}\; i\; \backslash \; right)\}\}$	0,9472 + 0,3208i
$4\; я\; =\; я\; (3\; я)\; \{\backslash \; textstyle\; \{\}\; ^\; \{4\}\; я\; =\; я\; ^\; \{\backslash \; влево\; (\{\}\; ^\; \{3\}\; я\; \backslash \; г\; ight)\}\}$	0,0501 + 0,6021i
$5\; i\; =\; i\; (4\; i)\; \{\; \backslash \; textstyle\; \{\}\; ^\; \{5\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{4\}\; i\; \backslash \; right)\}\}$	0,3872 + 0,0305i
$6\; i\; =\; i\; (5\; i)\; \{\; \backslash \; textstyle\; \{\}\; ^\; \{6\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{5\}\; i\; \backslash \; right)\}\}$	0,7823 + 0,5446i
$7\; i\; =\; i\; (6\; i)\; \{\; \backslash \; textstyle\; \{\}\; ^\; \{7\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{6\}\; i\; \backslash \; right)\}\}$	0,1426 + 0,4005i
$8\; i\; =\; i\; (7\; i)\; \{\; \backslash \; textstyle\; \{\}\; ^\; \{8\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{7\}\; i\; \backslash \; right)\}\}$	0,5198 + 0,1184i
$9\; i\; =\; i\; (8\; i)\; \{\; \backslash \; textstyle\; \{\}\; ^\; \{9\}\; i\; =\; i\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{8\}\; i\; \backslash \; right)\}\}$	0,5686 + 0,6051i

Решение обратное отношение, как и в предыдущем разделе, дает ожидаемые i = 1 и i = 0, с отрицательными значениями n, дающими бесконечные результаты на мнимой оси. Построенная на комплексной плоскости , вся последовательность закручивается по спирали до предела 0,4383 + 0,3606i, что можно интерпретировать как значение, где n бесконечно.

Такие последовательности тетраций изучались со времен Эйлера, но плохо изучены из-за их хаотического поведения. Большинство опубликованных исследований исторически сосредоточено на сходимости бесконечно повторяющейся экспоненциальной функции. Текущим исследованиям в значительной степени способствовало появление мощных компьютеров с фракталом и программным обеспечением для символьной математики. Многое из того, что известно о тетрации, получено из общих знаний о сложной динамике и конкретных исследований экспоненциального отображения.

Расширения области для разных высот

Бесконечные высоты

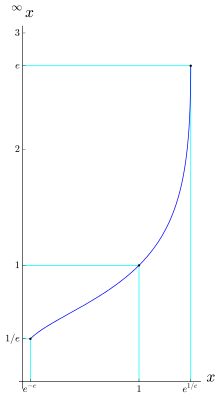
$lim\; n\; \to \; \infty \; nx\; \{\backslash \; displaystyle\; \backslash \; textstyle\; \backslash \; lim\; \_\; \{n\; \backslash \; rightarrow\; \backslash \; infty\}\; \{\}\; ^\; \{n\}\; x\}$бесконечно повторяющейся экспоненты сходится для оснований $(e\; -\; 1)\; e\; \le \; x\; \le \; е\; (е\; -\; 1)\; \{\backslash \; Displaystyle\; \backslash \; textstyle\; \backslash \; влево\; (е\; ^\; \{-\; 1\}\; \backslash \; вправо)\; ^\; \{е\}\; \backslash \; Leq\; х\; \backslash \; Leq\; е\; ^\; \{\backslash \; влево\; (е\; ^\; \{-\; 1\}\; \backslash \; вправо)\}\}$ Функция $|\; W\; (-\; ln\; \; z)\; -\; ln\; \; z\; |\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{W\}\; (-\; \backslash \; ln\; \{z\})\}\; \{-\; \backslash \; ln\; \{z\}\}\}\; \backslash \; right\; |\}$на комплексной плоскости, показывая вещественнозначная бесконечно повторяемая экспоненциальная функция (черная кривая)

Тетрация может быть расширена до бесконечной высоты; т.е. для определенных значений a и n в $n\; a\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; a\}$существует четко определенный результат для бесконечного n. Это связано с тем, что для оснований в пределах определенного интервала тетрация сходится к конечному значению, поскольку высота стремится к бесконечности. Например, $2\; 2\; 2\; \cdot \; \cdot \; \cdot \; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\; \backslash \; cdot\}\}\}\}\}\}$сходится к 2, и поэтому можно сказать, что он равен 2. Тенденцию к 2 можно увидеть, оценив небольшую конечную башню:

$2\; 2\; 2\; 2\; 2\; 1,414\; \approx \; 2\; 2\; 2\; 2\; 1,63\; \approx \; 2\; 2\; 2\; 1,76\; \approx \; 2\; 2\; 1,84\; \approx \; 2\; 1,89\; \approx \; 1,93\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\{\; \backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{1.414\}\}\}\}\}\; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\; \}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{1.63\}\}\}\}\; \backslash \backslash \; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\; \backslash \; sqrt\; \{2\}\}\; ^\; \{1.76\}\}\}\; \backslash \backslash \; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{\{\backslash \; sqrt\; \{2\}\}\; ^\; \{1.84\}\}\; \backslash \backslash \; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{2\}\}\; ^\; \{1.89\}\; \backslash \backslash \; \backslash \; приблизительно\; 1,93\; \backslash \; end\; \{align\}\}\}$

В общем, бесконечно повторяемая экспонента $xx\; \cdot \; \cdot \; \cdot \; \{\backslash \; displaystyle\; x\; ^\; \{x\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\}\}\}\}\; \backslash !\; \backslash !\}$, определяемый как предел $nx\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; x\}$, когда n стремится к бесконечности, сходится при e ≤ x ≤ e, примерно в интервале от 0,066 до 1,44, результат показан Леонардом Эйлером. Предел, если он существует, является положительным действительным решением уравнения y = x. Таким образом, x = y. Предел, определяющий бесконечную тетрацию x, не может сходиться при x>e, потому что максимум y равен e.

Это может быть расширено до комплексных чисел z следующим определением:

$\infty \; z\; =\; zz\; \cdot \; \cdot \; \cdot \; =\; W\; (-\; ln\; \; z)\; -\; ln\; \; z,\; \{\backslash \; displaystyle\; \{\}\; ^\; \{\backslash \; infty\; \}\; z\; =\; z\; ^\; \{z\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\}\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{W\}\; (-\; \backslash \; ln\; \{z\})\}\; \{-\; \backslash \; ln\; \{z\}\}\; \}\; ~,\}$

где W представляет функцию W Ламберта.

В качестве предела y = x (если существует, т.е. для e < x < e) must satisfy x = y we see that x ↦ y = x is (the lower branch of) the inverse function of y ↦ x = y.

Отрицательные высоты

Мы можем использовать рекурсивное правило для тетрация,

$k\; +\; 1\; a\; =\; a\; (ka),\; \{\backslash \; displaystyle\; \{^\; \{k\; +\; 1\}\; a\}\; =\; a\; ^\; \{\backslash \; left\; (\{^\; \{k\}\; a\}\; \backslash \; right)\},\}$

для доказательства $-\; 1\; a\; \{\backslash \; displaystyle\; \{\}\; ^\; \{-\; 1\}\; a\}$:

$ka\; =\; log\; a\; \; (k\; +\; 1\; a);\; \{\backslash \; displaystyle\; ^\; \{k\}\; a\; =\; \backslash \; log\; \_\; \{a\}\; \backslash \; left\; (^\; \{k\; +\; 1\}\; a\; \backslash \; right);\}$

Замена −1 вместо k дает

$-\; 1\; a\; =\; log\; a\; \; (0\; a)\; =\; log\; a\; \; 1\; =\; 0\; \{\backslash \; displaystyle\; \{\}\; ^\; \{-\; 1\}\; a\; =\; \backslash \; log\; \_\; \{a\}\; \backslash \; left\; (\{\}\; ^\; \{0\}\; a\; \backslash \; right)\; =\; \backslash \; log\; \_\; \{a\}\; 1\; =\; 0\}$.

Меньшие отрицательные значения не могут быть точно определены таким образом. Подстановка −2 вместо k в том же уравнен ии дает

$-\; 2\; a\; =\; log\; a\; \; (-\; 1\; a)\; =\; log\; a\; \; 0\; \{\backslash \; displaystyle\; \{\}\; ^\; \{-\; 2\}\; a\; =\; \backslash \; log\; \_\; \{a\}\; \backslash \; left\; (\{\}\; ^\; \{-\; 1\}\; a\; \backslash \; right)\; =\; \backslash \; log\; \_\; \{a\}\; 0\}$

который не вполне определен. Однако иногда их можно рассматривать как наборы.

Для $n\; =\; 1\; \{\backslash \; displaystyle\; n\; =\; 1\}$любое определение $-\; 1\; 1\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \{^\; \{-\; 1\}\; 1\}\}$соответствует правилу, потому что

$0\; 1\; =\; 1\; =\; 1\; n\; \{\backslash \; displaystyle\; \{^\; \{0\}\; 1\}\; =\; 1\; =\; 1\; ^\; \{\; n\}\}$для любого $n\; =\; -\; 1\; 1\; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; n\; =\; \{^\; \{-\; 1\}\; 1\}\}$.

Реальные высоты

При этом время не существует общепринятого решения общей проблемы расширения тетрации до действительных или комплексных значений n. Однако к этому вопросу использовалось несколько подходов, и различные подходы изложены ниже.

В общем, проблема заключается в нахождении - для любого действительного a>0 - суперэкспоненциальной функции $f\; (x)\; =\; xa\; \{\backslash \; displaystyle\; \backslash ,\; f\; (x)\; =\; \{\}\; ^\; \{x\; \}\; a\}$над вещественным x>−2, которое удовлетворяет

• $-\; 1\; a\; =\; 0\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{-\; 1\}\; a\; =\; 0\}$
• $0\; a\; =\; 1\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{0\}\; a\; =\; 1\}$
• $xa\; =\; a\; (x\; -\; 1\; a)\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{x\}\; a\; =\; a\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{x-\; 1\}\; a\; \backslash \; right)\}\}$для всех действительных $x>-\; 1.\; \{\backslash \; displaystyle\; x>-1.\}$

Чтобы найти более естественное расширение, одно или несколько дополнительных требований обычно требуются. Обычно это некоторый набор следующих элементов:

• Требование непрерывности (обычно просто $xa\; \{\backslash \; displaystyle\; \{\}\; ^\; \{x\}\; a\}$непрерывно в обеих переменных для $x>0\; \{\backslash \; displaystyle\; x>0\}$).
• Требование дифференцируемости (может быть однократно, дважды, k раз или бесконечно дифференцируемым по x).
• Требование регулярности (подразумевающее дважды дифференцируемость по x), которое:

$(d\; 2\; dx\; 2\; f\; (x)>0)\; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{d\; ^\; \{2\}\}\; \{dx\; ^\; \{2\}\}\}\; f\; (x)>0\; \backslash \; right)\}$для всех $x>0\; \{\backslash \; displaystyle\; x>0\}$

Четвертое требование различается от автора к автору и от подходов. Есть два основных подхода к расширению тетрации до реальных высот; один основан на требовании регулярности, а другой основан на требовании дифференцируемости. Эти два подхода кажутся настолько разными, что их невозможно согласовать, поскольку они дают результаты, несовместимые друг с другом.

Когда $xa\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{x\}\; a\}$определено для интервала длины один, вся функция легко следует для всех x>−2.

Линейное приближение для реальных высот

$xe\; \{\backslash \; displaystyle\; \backslash ,\; \{\}\; ^\; \{x\}\; e\}$с использованием линейного приближения.

A линейное приближение (решение требование непрерывности, приближение к требованию дифференцируемости) определяется как:

, следовательно:

Значения линейного приближения

Приближение	Домен
$xa\; \approx \; x\; +\; 1\; \{\backslash \; textstyle\; \{\}\; ^\; \{x\}\; a\; \backslash \; приблизительно\; x\; +\; 1\}$	для −1 < x < 0
$xa\; \approx \; ax\; \{\backslash \; textstyle\; \{\}\; ^\; \{x\}\; a\; \backslash \; приблизительно\; a\; ^\; \{x\}\}$	для 0 < x < 1
$xa\; \approx \; aa\; (x\; -\; 1)\; \{\backslash \; textstyle\; \{\}\; ^\; \{x\}\; a\; \backslash \; приблизительно\; a\; ^\; \{a\; ^\; \{(x-\; 1)\}\}\}$	для 1 < x < 2

и так далее. Однако она дифференцируема только кусочно; при целочисленных значениях x производная умножается на $ln\; \; a\; \{\backslash \; displaystyle\; \backslash \; ln\; \{a\}\}$. Он непрерывно дифференцируется для $x>-\; 2\; \{\backslash \; displaystyle\; x>-2\}$если и только если $a\; =\; e\; \{\backslash \; displaystyle\; a\; =\; e\}$. Например, используя эти методы $\pi \; 2\; e\; \approx \; 5,868...\; \{\backslash \; displaystyle\; \{\}\; ^\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; e\; \backslash \; приблизительно\; 5,868...\}$и $-\; 4,3\; 0,5\; \approx \; 4.03335...\; \{\backslash \; displaystyle\; \{\}\; ^\; \{-\; 4.3\}\; 0.5\; \backslash \; приблизительно\; 4.03335...\}$

Основная теорема в статье Хушманда гласит: Пусть . Если $f:\; (-\; 2,\; +\; \infty )\; \to \; R\; \{\backslash \; displaystyle\; f:\; (-\; 2,\; +\; \backslash \; infty)\; \backslash \; rightarrow\; \backslash \; mathbb\; \{R\}\}$непрерывно и удовлетворяет условиям:

• $f\; (x)\; =\; af\; (x\; -\; 1)\; для\; всех\; x>-\; 1,\; f\; (0)\; =\; 1,\; \{\backslash \; displaystyle\; f\; (x)\; =\; a\; ^\; \{f\; (x-1)\}\; \backslash ;\; \backslash ;\; \{\backslash \; text\; \{для\; всех\}\}\; \backslash ;\; \backslash ;\; x>-1,\; \backslash ;\; f\; (0)\; =\; 1,\}$
• $f\; \{\backslash \; отображает\; tyle\; f\}$дифференцируема на (−1, 0),
• $f\; \prime \; \{\backslash \; displaystyle\; f\; ^\; \{\backslash \; prime\}\}$- неубывающая или невозрастающая функция на (−1, 0),
• $f\; \prime \; (0\; +)\; =\; (ln\; \; a)\; f\; \prime \; (0\; -)\; или\; f\; \prime \; (-\; 1\; +)\; =\; f\; \prime \; (0\; -).\; \{\backslash \; displaystyle\; f\; ^\; \{\backslash \; prime\}\; \backslash \; left\; (0\; ^\; \{+\}\; \backslash \; right)\; =\; (\backslash \; ln\; a)\; f\; ^\; \{\backslash \; prime\}\; \backslash \; left\; (0\; ^\; \{-\}\; \backslash \; right)\; \{\backslash \; text\; \{или\}\}\; f\; ^\; \{\backslash \; prime\}\; \backslash \; left\; (-1\; ^\; \{+\}\; \backslash \; right)\; =\; f\; ^\; \{\backslash \; prime\}\; \backslash \; left\; (0\; ^\; \{-\}\; \backslash \; right).\}$

затем $f\; \{\backslash \; displaystyle\; f\; \}$однозначно определяется с помощью уравнения

$f\; (x)\; =\; exp\; a\; [x]\; \; (a\; (x))\; =\; exp\; a\; [x\; +\; 1]\; \; ((x))\; для\; всех\; x>-\; 2,\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; exp\; \_\; \{a\}\; ^\; \{[x]\}\; \backslash \; left\; (a\; ^\; \{(x)\}\; \backslash \; right)\; =\; \backslash \; exp\; \_\; \{a\}\; ^\; \{[x\; +\; 1\; ]\}\; ((x))\; \backslash \; quad\; \{\backslash \; text\; \{для\; всех\}\}\; \backslash ;\; \backslash ;\; x>-2,\}$

где $(x)\; =\; x\; -\; [x]\; \{\backslash \; displaystyle\; (x)\; =\; x-\; [x]\}$обозначает дробную часть x и $exp\; a\; [x]\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{a\}\; ^\; \{[x]\}\}$- это $[x]\; \{\backslash \; displaystyle\; [x]\}$-итерационная функция функции $exp\; a\; \{\backslash \; displaystyle\; \backslash \; exp\; \_\; \{a\}\}$.

Доказательство того, что вторая из четвертых условий тривиально следует, что f - линейная функция на [−1, 0].

Линейная аппроксимация функции естественной тетрации $xe\; \{\backslash \; displaystyle\; \{\}\; ^\; \{x\}\; e\}$непрерывно дифференцируема, но ее вторая производная не существует при целых значениях ее аргумент. Хушманд вывел для него другую теорему уникальности, в которой говорится:

Если $f:\; (-\; 2,\; +\; \infty )\; \to \; R\; \{\backslash \; displaystyle\; f:\; (-\; 2,\; +\; \backslash \; infty)\; \backslash \; rightarrow\; \backslash \; mathbb\; \{R\; \}\}$- непрерывная функция, которая удовлетворяет:

• $f\; (x)\; =\; ef\; (x\; -\; 1)\; для\; всех\; x>-\; 1,\; f\; (0)\; =\; 1,\; \{\backslash \; displaystyle\; f\; (x)\; =\; e\; ^\; \{f\; (x-1)\}\; \backslash ;\; \backslash ;\; \{\backslash \; text\; \{для\; всех\}\}\; \backslash ;\; \backslash ;\; x>-1,\; \backslash ;\; f\; (0)\; =\; 1,\}$
• $f\; \{\backslash displaystyle\; f\}$is convex on (−1, 0),
• $f\; \prime \; (\; 0\; -)\; \le \; f\; \prime \; (\; 0\; +).\; \{\backslash displaystyle\; f^\{\; \backslash prime\; \}\backslash left(0^\{-\}\backslash right)\backslash leq\; f^\{\backslash prime\; \}\backslash left(0^\{+\}\backslash right).\}$

then $f\; =\; uxp\; \{\backslash displaystyle\; f=\; \{\backslash text\{uxp\}\}\}$. [Here $f\; =\; uxp\; \{\backslash displaystyle\; f=\{\backslash text\{uxp\}\}\}$is Hooshmand's name for the linear approximation to the natural tetration function.]

The proof is much the same as before; the recursion equation ensures that $f\; \prime \; (\; -\; 1\; +)\; =\; f\; \prime \; (\; 0\; +),\; \{\backslash displaystyle\; f^\{\backslash prime\; \}(-1^\{+\})=f^\{\backslash prime\; \}(0^\{+\}),\}$and then the convexity condition implies that $f\; \{\backslash displaystyle\; f\}$is linear on (−1, 0).

Therefore, the linear approximation to natural tetration is the only solution of the equation $f\; (\; x)\; =\; e\; f\; (\; x\; -\; 1)\; (\; x>-\; 1)\; \{\backslash d\; isplaystyle\; f(x)=e^\{f(x-1)\}\backslash ;\backslash ;(x>-1)\}$and $f\; (\; 0)\; =\; 1\; \{\backslash displaystyle\; f(0)=1\}$which is convex on (−1, +∞). All other sufficiently-differentiable solutions must have an inflection point on the interval (−1, 0).

Higher order approximations for real heights

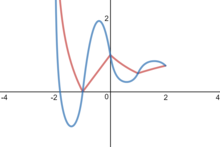
A comparison of the linear and quadratic approximations (in red and blue respectively) of the function $x\; 0.5\; \{\backslash displaystyle\; ^\{x\}0.5\}$, from x = −2 to x = 2.

Beyond linear approximations, a quadratic approximation (to the differentiability requirement) is given by:

который дифференцируется для всех $x>0\; \{\backslash \; displaystyle\; x>0\}$, но не дифференцируемый дважды. Например, $1\; 2\; 2\; \approx \; 1,45933...\; \{\backslash \; displaystyle\; \{\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; 2\; \backslash \; приблизительно\; 1,45933...\}$Если $a\; =\; e\; \{\backslash \; displaystyle\; a\; =\; e\}$это то же самое, что и линейное приближение.

Из-за способа вычисления эта функция не "сокращается", в отличие от показателей степени, где $(a\; 1\; n)\; n\; =\; a\; \{\backslash \; displaystyle\; \backslash \; left\; (a\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; right)\; ^\; \{n\}\; =\; a\}$. А именно,

$n\; (1\; na)\; =\; (1\; na)\; (1\; na)\; \cdot \; \cdot \; \cdot \; \cdot \; (1\; na)\; ⏟\; n\; \ne \; a\; \{\backslash \; displaystyle\; \{\}\; ^\; \{n\}\; \backslash \; left\; (\{\}\; ^\; \{\backslash \; frac\; \{\; 1\}\; \{n\}\}\; a\; \backslash \; right)\; =\; \backslash \; underbrace\; \{\backslash \; left\; (\{\}\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; a\; \backslash \; right)\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{\backslash \; frac\; \{1\}\; \{n\; \}\}\; a\; \backslash \; right)\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; cdot\; ^\; \{\backslash \; left\; (\{\}\; ^\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; a\; \backslash \; right)\}\}\}\}\}\}\; \}\; \_\; \{n\}\; \backslash \; neq\; a\}$.

Так же, как есть квадратичное приближение, существуют также кубические приближения и методы обобщения на приближения степени n, хотя они намного более громоздки.

Комплексные высоты

Рисование аналитического расширения $f\; =\; F\; (x\; +\; iy)\; \{\backslash \; displaystyle\; f\; =\; F\; (x\; +\; \{\backslash \; rm\; \{i\}\}\; y)\}$тетрации на комплексной плоскости. Уровни $|\; f\; |\; =\; 1,\; e\; \pm \; 1,\; e\; \pm \; 2,\dots \; \{\backslash \; displaystyle\; |\; f\; |\; =\; 1,\; e\; ^\; \{\backslash \; pm\; 1\},\; e\; ^\; \{\backslash \; pm\; 2\},\; \backslash \; ldots\}$и уровни $arg\; \; (f)\; =\; 0,\; \pm \; 1,\; \pm \; 2,\dots \; \{\backslash \; displaystyle\; \backslash \; arg\; (f)\; =\; 0,\; \backslash \; pm\; 1,\; \backslash \; pm\; 2,\; \backslash \; ldots\}$показаны толстыми кривыми.

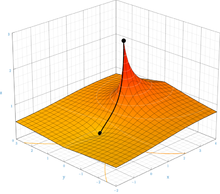
Теперь доказано, что существует единственная функция F, которая является решением уравнения F (z + 1) = exp (F (z)) и удовлетворяет дополнительным условиям, что F (0) = 1 и F (z) приближается к неподвижным точкам логарифма (примерно 0,318 ± 1,337i), когда z приближается к ± i∞, и что F голоморфно во всей комплексной z-плоскости, за исключением часть действительной оси при z ≤ −2. Это доказательство подтверждает предыдущую гипотезу . Построение такой функции было первоначально продемонстрировано Кнезером в 1950 году. Комплексное отображение этой функции показано на рисунке справа. Доказательство также работает для других оснований, кроме e, если основание больше $e\; 1\; e\; \approx \; 1,445\; \{\backslash \; displaystyle\; e\; ^\; \{\backslash \; frac\; \{1\}\; \{e\}\}\; \backslash \; приблизительно\; 1,445\}$. Последующие работы продлены