Принцип Франка – Кондона

редактировать

Рисунок 1. Энергетическая диаграмма принципа Франка – Кондона. Поскольку электронные переходы очень быстры по сравнению с ядерными движениями, предпочтение отдается колебательным уровням, когда они соответствуют минимальному изменению ядерных координат. потенциальные ямы показаны в пользу переходов между v = 0 и v = 2.

Franck - принцип Кондона является правило спектроскопии и квантовой химии, которое объясняет интенсивность вибронных переходов. Вибронные переходы - это одновременные изменения электронных и колебательных уровней энергии молекулы из-за поглощения или испускания фотона соответствующей энергии. Принцип гласит, что во время электронного перехода изменение с одного колебательного уровня энергии на другой будет более вероятно, если две колебательные волны функции перекрываются более значительно.

Содержание

1 Обзор
2 Развитие принципа
3 Квантовая механика
4 Метафоры Франка – Кондона в спектроскопии
- 4.1 Принцип Франка – Кондона для фононов
- 4.2 Франк– Принцип Кондона в сольватации
5 См. Также
6 Ссылки
7 Дополнительная литература
8 Внешние ссылки

Обзор

Рисунок 2. Схематическое изображение спектров поглощения и флуоресценции, соответствующих энергетическая диаграмма на рисунке 1. Симметрия обусловлена одинаковой формой потенциальных ям основного и возбужденного состояний. Узкие линии обычно наблюдаются только в спектрах разреженных газов. Более темные кривые представляют собой неоднородное уширение тех же переходов, которые имеют место в жидкостях и твердых телах. Электронные переходы между низшими колебательными уровнями электронных состояний (переход 0–0) имеют одинаковую энергию как при поглощении, так и при флуоресценции.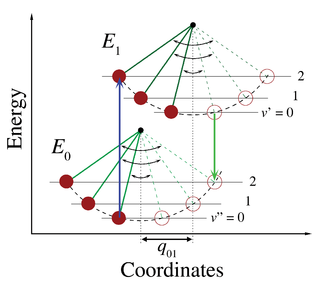

Рис. 3. Полуклассическая аналогия маятника принципа Франка-Кондона. Вибронные переходы разрешены в классических поворотных точках, потому что и импульс, и ядерные координаты соответствуют на двух представленных уровнях энергии. На этой иллюстрации предпочтение отдается колебательным переходам 0–2.

Принцип Франка – Кондона имеет хорошо устоявшуюся полуклассическую интерпретацию, основанную на первоначальном вкладе Джеймса Франка. Электронные переходы по существу мгновенны по сравнению с временной шкалой ядерных движений, поэтому, если молекула должна перейти на новый колебательный уровень во время электронного перехода, этот новый колебательный уровень должен быть мгновенно совместим с положениями ядер и импульсы колебательного уровня молекулы в исходном электронном состоянии. В полуклассической картине колебаний (колебаний) простого гармонического осциллятора необходимые условия могут возникать в точках поворота, где импульс равен нулю.

Классически принцип Франка – Кондона представляет собой приближение, согласно которому электронный переход наиболее вероятен без изменения положения ядер в молекулярном объекте и его окружении. Результирующее состояние называется состоянием Франка – Кондона, а соответствующий переход - вертикальным переходом. Квантово-механическая формулировка этого принципа состоит в том, что интенсивность вибронного перехода пропорциональна квадрату интеграла перекрытия между колебательными волновыми функциями двух состояний, участвующих в переходе.

— IUPAC Сборник химической терминологии, 2-е издание (1997)

В изображении квантовой механики колебательные уровни и колебательные волновые функции - это уровни квантовых гармонических осцилляторов или более сложные приближения к потенциальная энергия молекул, такая как потенциал Морзе. На рис. 1 показан принцип Франка – Кондона для электронно-колебательных переходов в молекуле с функциями потенциальной энергии типа Морзе как в основном, так и в возбужденном электронном состояниях. В низкотемпературном приближении молекула стартует на колебательном уровне v = 0 основного электронного состояния и после поглощения фотона необходимой энергии переходит в возбужденное электронное состояние. Электронная конфигурация нового состояния может привести к смещению положения равновесия ядер, составляющих молекулу. На рисунке этот сдвиг ядерных координат между основным и первым возбужденным состоянием обозначен как q 01. В простейшем случае двухатомной молекулы ось ядерных координат относится к межъядерному разделению. Вибронный переход обозначен вертикальной стрелкой из-за предположения о постоянстве ядерных координат во время перехода. Вероятность того, что молекула может оказаться на каком-либо конкретном колебательном уровне, пропорциональна квадрату (вертикального) перекрытия колебательных волновых функций исходного и конечного состояний (см. Раздел квантово-механической формулировки ниже). В электронном возбужденном состоянии молекулы быстро релаксируют на самый нижний колебательный уровень самого низкого состояния электронного возбуждения (правило Каша ), а оттуда могут распадаться в основное электронное состояние посредством излучения фотонов. Принцип Франка – Кондона в равной степени применяется к поглощению и флуоресценции.

. Применимость принципа Франка – Кондона как к поглощению, так и к флуоресценции вместе с правилом Каша приводит к показанной приблизительной зеркальной симметрии на рис. 2. Колебательная структура молекул в холодном разреженном газе наиболее отчетливо видна из-за отсутствия неоднородного уширения отдельных переходов. Вибронные переходы изображены на рисунке 2 как узкие, равномерно расположенные лоренцевы формы линий. Равный интервал между колебательными уровнями имеет место только в случае параболического потенциала простых гармонических осцилляторов, в более реалистичных потенциалах, таких как показанные на рисунке 1, интервал энергии уменьшается с увеличением энергии колебаний. Электронные переходы в низшие колебательные состояния и из них часто называют переходами 0–0 (ноль-ноль) и имеют одинаковую энергию как для поглощения, так и для флуоресценции.

Развитие принципа

В отчете, опубликованном в 1926 году в Transactions of the Faraday Society, Джеймс Франк рассматривал механизмы фотонного -индуцированные химические реакции. Предполагаемый механизм - возбуждение молекулы фотоном с последующим столкновением с другой молекулой в течение короткого периода возбуждения. Вопрос был в том, могла ли молекула разбиться на фотопродукты за один шаг, поглощение фотона, и без столкновения. Чтобы молекула распалась, она должна получить от фотона колебательную энергию, превышающую энергию диссоциации, то есть энергию разрыва химической связи. Однако, как было известно в то время, молекулы будут поглощать только энергию, соответствующую разрешенным квантовым переходам, и нет колебательных уровней выше уровня энергии диссоциации потенциальной ямы. Поглощение фотонов высоких энергий приводит к переходу в более высокое электронное состояние вместо диссоциации. Изучая, сколько колебательной энергии может получить молекула, когда она возбуждена на более высокий электронный уровень, и может ли этой колебательной энергии быть достаточно, чтобы немедленно разорвать молекулу, он нарисовал три диаграммы, представляющие возможные изменения энергии связи между нижними электронными состояние и более высокие электронные состояния.

Диаграмма I. показывает сильное ослабление связи при переходе из нормального состояния n в возбужденные состояния a и a '. Здесь D>D 'и D'>D ". В то же время положение равновесия ядер смещается с возбуждением к большим значениям r. Если перейти от положения равновесия (минимума потенциальной энергии) n кривая вертикально [курсив добавлен] вверх к кривым a на диаграмме I. частицы будут иметь потенциальную энергию больше, чем D ', и будут разлетаться. В этом случае мы имеем очень большое изменение в колебании энергия при возбуждении светом...

— Джеймс Франк, 1926

Джеймс Франк признал, что изменения в колебательных уровнях могут быть следствием мгновенного характера возбуждения на более высокие электронные уровни энергии и нового положения равновесия для ядерного взаимодействия Эдвард Кондон расширил это понимание за пределы фотореакций в статье 1926 года Physical Review под названием «Теория распределения интенсивности в ленточных системах». Здесь он формулирует полуклассическую формулировку в очень похожей манере. в его современный вид. Первый Совместная ссылка на Франка и Кондона в отношении нового принципа появляется в том же выпуске Physical Review за 1926 год в статье о полосовой структуре окиси углерода, написанной Раймондом Бирджем.

Рис. 5. Рисунок 1 в первой публикации Эдварда Кондона о том, что сейчас является принципом Франка – Кондона [Condon 1926]. Кондон решил наложить потенциальные кривые, чтобы проиллюстрировать метод оценки колебательных переходов.

Квантовомеханическая формулировка

Рассмотрим электрический дипольный переход из начального колебательного состояния (υ) земли электронный уровень (ε), $| ϵ v⟩ {\ displaystyle | \ epsilon v \ rangle}$ $| \ epsilon v \ rangle$ , в некоторое колебательное состояние (υ ′) возбужденного электронного состояния (ε ′), $| ϵ ′ v ′⟩ {\ displaystyle | \ epsilon 'v' \ rangle}$ $|\epsilon 'v'\rangle$ (см. обозначение бюстгальтера ). Оператор молекулярного диполя μ определяется зарядом (-e) и местоположением (ri) электронов, а также зарядами (+ Z j e) и положения (Rj) ядер :

μ = μ e + μ N = - e ∑ iri + e j Z j R j. {\ displaystyle {\ boldsymbol {\ mu}} = {\ boldsymbol {\ mu}} _ {e} + {\ boldsymbol {\ mu}} _ {N} = - e \ sum \ limits _ {i} {\ boldsymbol {r}} _ {i} + e \ sum \ limits _ {j} Z_ {j} {\ boldsymbol {R}} _ {j}.}

{\ boldsymbol {\ mu}} = {\ boldsymbol {\ mu}} _ {e} + {\ boldsymbol {\ mu}} _ {N} = - e \ sum \ limits _ {i} {\ boldsymbol {r}} _ {i} + e \ sum \ limits _ {j} Z_ {j} {\ boldsymbol {R}} _ {j}.

амплитуда вероятности P для переход между этими двумя состояниями определяется выражением

P = ⟨ψ ′ | μ | ψ⟩ знак равно ∫ ψ ′ ∗ μ ψ d τ, {\ Displaystyle P = \ left \ langle \ psi '\ right | {\ boldsymbol {\ mu}} \ left | \ psi \ right \ rangle = \ int {\ psi '^ {*}} {\ boldsymbol {\ mu}} \ psi \, d \ tau,}

P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle =\int {\psi '^{*}}{\boldsymbol {\mu }}\psi \,d\tau,

где $ψ {\ displaystyle \ psi}$ $\ psi$ и $ψ ′ { \ displaystyle \ psi '}$ $\psi '$ - это, соответственно, общие волновые функции начального и конечного состояния. Общие волновые функции являются продуктом отдельных колебательных (в зависимости от пространственных координат ядер) и электронного пространства и волновых функций спина :

ψ = ψ e ψ v ψ s. {\ displaystyle \ psi = \ psi _ {e} \ psi _ {v} \ psi _ {s}.}

\ psi = \ psi _ {e} \ psi _ {v} \ psi _ {s}.

Это разделение электронных и колебательных волновых функций является выражением приближения Борна – Оппенгеймера и является основным предположением принципа Франка – Кондона. Объединение этих уравнений приводит к выражению для амплитуды вероятности в терминах отдельного электронного пространства, спинового и колебательного вкладов:

P = ⟨ψ e ′ ψ v ′ ψ s ′ | μ | ψ е ψ v ψ s⟩ знак равно ∫ ψ e ′ ∗ ψ v ′ ∗ ψ s ′ ∗ (μ e + μ N) ψ e ψ v ψ sd τ {\ displaystyle P = \ left \ langle \ psi _ {e} '\ psi _ {v}' \ psi _ {s} '\ right | {\ boldsymbol {\ mu}} \ left | \ psi _ {e} \ psi _ {v} \ psi _ {s} \ right \ rangle = \ int \ psi _ {e} '^ {*} \ psi _ {v}' ^ {*} \ psi _ {s} '^ {*} ({\ boldsymbol {\ mu}} _ {e} + {\ boldsymbol {\ mu}} _ {N}) \ psi _ {e} \ psi _ {v} \ psi _ {s} \, d \ tau}

P=\left\langle \psi _{e}'\psi _{v}'\psi _{s}'\right|{\boldsymbol {\mu }}\left|\psi _{e}\psi _{v}\psi _{s}\right\rangle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}({\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N})\psi _{e}\psi _{v}\psi _{s}\,d\tau

= ∫ ψ e ′ ∗ ψ v ′ ∗ ψ s ′ ∗ μ e ψ e ψ v ψ sd τ + ∫ ψ e ′ ∗ ψ v ′ ∗ ψ s ′ ∗ μ N ψ e ψ v ψ sd τ {\ displaystyle = \ int \ psi _ {e} ' ^ {*} \ psi _ {v} '^ {*} \ psi _ {s}' ^ {*} {\ boldsymbol {\ mu}} _ {e} \ psi _ {e} \ psi _ {v} \ psi _ {s} \, d \ tau + \ int \ psi _ {e} '^ {*} \ psi _ {v}' ^ {*} \ psi _ {s} '^ {*} {\ boldsymbol {\ mu}} _ {N} \ psi _ {e} \ psi _ {v} \ psi _ {s} \, d \ tau}

=\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\psi _{s}\,d\tau +\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}{\boldsymbol {\mu }}_{N}\psi _{e}\psi _{v}\psi _{s}\,d\tau

= ∫ ψ v ′ ∗ ψ vd τ n ⏟ Franck – Condon фактор ∫ ψ e ′ ∗ μ e ψ ed τ e ⏟ правило выбора орбиты ∫ ψ s ′ ∗ ψ sd τ s ⏟ правило выбора спина + ∫ ψ e ′ ∗ ψ ed τ e ⏟ 0 ∫ ψ v ′ ∗ μ N ψ vd τ v ∫ ψ s ′ ∗ ψ sd τ s. {\ displaystyle = \ underbrace {\ int \ psi _ {v} '^ {*} \ psi _ {v} \, d \ tau _ {n}} _ {\ displaystyle {{\ text {Franck – Condon}} \ atop {\ text {factor}}}} \ underbrace {\ int \ psi _ {e} '^ {*} {\ boldsymbol {\ mu}} _ {e} \ psi _ {e} \, d \ tau _ {e}} _ {\ displaystyle {{\ text {orbital}} \ atop {\ text {selection rule}}}} \ underbrace {\ int \ psi _ {s} '^ {*} \ psi _ {s } \, d \ tau _ {s}} _ {\ displaystyle {{\ text {spin}} \ atop {\ text {selection rule}}}} + \ underbrace {\ int \ psi _ {e} '^ { *} \ psi _ {e} \, d \ tau _ {e}} _ {\ displaystyle 0} \ int \ psi _ {v} '^ {*} {\ boldsymbol {\ mu}} _ {N} \ psi _ {v} \, d \ tau _ {v} \ int \ psi _ {s} '^ {*} \ psi _ {s} \, d \ tau _ {s}.}

=\underbrace {\int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}} _{\displaystyle {{\text{Franck–Condon}} \atop {\text{factor}}}}\underbrace {\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}} _{\displaystyle {{\text{orbital}} \atop {\text{selection rule}}}}\underbrace {\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}} _{\displaystyle {{\text{spin}} \atop {\text{selection rule}}}}+\underbrace {\int \psi _{e}'^{*}\psi _{e}\,d\tau _{e}} _{\displaystyle 0}\int \psi _{v}'^{*}{\boldsymbol {\mu }}_{N}\psi _{v}\,d\tau _{v}\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}.

Спин- независимая часть исходного интеграла здесь аппроксимируется как произведение двух интегралов:

∬ ψ v ′ ∗ ψ e ′ ∗ μ e ψ e ψ vd τ ed τ n ≈ ∫ ψ v ′ ∗ ψ vd τ n ∫ ψ e ′ ∗ μ e ψ ed τ e. {\ displaystyle \ iint \ psi _ {v} '^ {*} \ psi _ {e}' ^ {*} {\ boldsymbol {\ mu}} _ {e} \ psi _ {e} \ psi _ {v } \, d \ tau _ {e} d \ tau _ {n} \ приблизительно \ int \ psi _ {v} '^ {*} \ psi _ {v} \, d \ tau _ {n} \ int \ psi _ {e} '^ {*} {\ boldsymbol {\ mu}} _ {e} \ psi _ {e} \, d \ tau _ {e}.}

\iint \psi _{v}'^{*}\psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v}\,d\tau _{e}d\tau _{n}\approx \int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}.

Эта факторизация была бы точной, если бы интеграл $∫ ψ е ′ ∗ μ е ψ ed τ е {\ Displaystyle \ int \ psi _ {e} '^ {*} {\ boldsymbol {\ mu}} _ {e} \ psi _ {e} \, d \ tau _ {e}}$ $\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}$ по пространственным координатам электронов не будет зависеть от ядерных координат. Однако в приближении Борна – Оппенгеймера $ψ e {\ displaystyle \ psi _ {e}}$ $\ psi _ {e}$ и $ψ e ′ {\ displaystyle \ psi '_ {e}}$ $\psi '_{e}$ действительно зависят (параметрически) от ядерных координат, так что интеграл (так называемая поверхность диполя перехода) является функцией ядерных координат. Поскольку зависимость обычно довольно гладкая, ею пренебрегают (т.е. часто допускается предположение о независимости поверхности диполя перехода от ядерных координат, называемое приближением Кондона).

Первый интеграл после знака «плюс» равен нулю, поскольку электронные волновые функции разных состояний ортогональны. Остающийся - произведение трех интегралов. Первый интеграл - это интеграл колебательного перекрытия, также называемый фактором Франка – Кондона . Оставшиеся два интеграла, вносящие вклад в амплитуду вероятности, определяют электронные пространственные и спиновые правила отбора.

Принцип Франка – Кондона - это утверждение о разрешенных колебательных переходах между двумя различными электронными состояниями; другие квантово-механические правила выбора могут снизить вероятность перехода или вообще запретить его. В приведенном выше выводе правила ротационного отбора не учитывались. Вращательные вклады можно наблюдать в спектрах газов, но они сильно подавлены в жидкостях и твердых телах.

Должно быть ясно, что квантово-механическая формулировка принципа Франка – Кондона является результатом ряда приближений, в основном предположения об электрическом дипольном переходе и приближения Борна – Оппенгеймера. Более слабые магнитные дипольные и электрические квадрупольные электронные переходы наряду с неполной достоверностью факторизации полной волновой функции на ядерные, электронные пространственные и спиновые волновые функции означают, что правила отбора, включая фактор Франка – Кондона, не являются строго наблюдаемый. Для любого данного перехода значение P определяется всеми правилами выбора, однако спин-отбор является наибольшим фактором, за которым следуют электронные правила выбора. Фактор Франка – Кондона только слабо модулирует интенсивность переходов, т.е. вносит вклад с коэффициентом порядка 1 в интенсивность полос, порядок величины которых определяется другими правилами отбора. В таблице ниже приведены диапазоны коэффициентов экстинкции для возможных комбинаций разрешенных и запрещенных правил выбора вращения и орбиты.

Интенсивности электронных переходов
	Диапазон значений коэффициента экстинкции (ε) (моль cm )
Спин и орбитально разрешенные	от 10 до 10
Спин разрешен но орбитально запрещен	от 10 до 10
Спин запрещен, но разрешен по орбите	от 10 до 10

метафоры Франка – Кондона в спектроскопии

Принцип Франка – Кондона, в своей канонической форме применяется только к изменениям колебательных уровней молекулы в ходе изменения электронных уровней в результате поглощения или испускания фотона. Физическая интуиция этого принципа основана на идее, что ядерные координаты атомы, составляющие молекулу, не успевают измениться в течение очень короткого промежутка времени, связанного с электронным переходом. Однако эта физическая интуиция может быть и действительно обычно распространяется на взаимодействия между поглощающими или излучающими свет молекулами (хромофоры ) и их окружение. Метафоры Франка – Кондона уместны заставляют молекулы часто сильно взаимодействовать с окружающими молекулами, особенно в жидкостях и твердых телах, и эти взаимодействия изменяют ядерные координаты хромофора способами, очень похожими на молекулярные колебания, рассматриваемые в соответствии с принципом Франка-Кондона.

Рисунок 6. Энергетическая диаграмма электронного перехода с фононной связью по конфигурационной координате q i, нормальная мода решетки. Стрелки вверх показывают поглощение без фононов и с тремя фононами. Стрелки вниз показывают симметричный процесс излучения.

Принцип Франка – Кондона для фононов

Ближайшая аналогия Франка – Кондона связана с взаимодействием фононов (квантов колебаний решетки ) с электронными переходами хромофоров, внедренных в решетку в качестве примесей. В этой ситуации переходы на более высокие электронные уровни могут иметь место, когда энергия фотона соответствует чисто электронной энергии перехода или чисто электронной энергии перехода плюс энергия одного или нескольких решеточных фононов. В низкотемпературном приближении излучение происходит с бесфононного уровня возбужденного состояния на бесфононный уровень основного состояния или на более высокие фононные уровни основного состояния. Как и в принципе Франка – Кондона, вероятность переходов с участием фононов определяется перекрытием волновых функций фононов на начальном и конечном уровнях энергии. Для принципа Франка – Кондона, применяемого к фононным переходам, метка горизонтальной оси на рисунке 1 заменена на рисунке 6 на конфигурационную координату для нормальной моды. Режим решетки $qi {\ displaystyle q_ {i}}$ $q_ {i}$ потенциальная энергия на рисунке 6 представлена как энергия гармонического осциллятора, а расстояние между уровнями фононов ( $ℏ Ω i {\ displaystyle \ hbar \ Omega _ {i}}$ $\ hbar \ Omega _ {i}$ ) определяется параметрами решетки. Поскольку энергия одиночных фононов, как правило, довольно мала, бесфононные переходы или переходы с несколькими фононами могут наблюдаться только при температурах ниже примерно 40 кельвинов.

См. нулевые фононные линии и фононные боковые полосы для дальнейшего детали и ссылки.

Принцип Франка – Кондона в сольватации

Рисунок 7. Энергетическая диаграмма, иллюстрирующая принцип Франка – Кондона, применяемый к сольватации хромофоров. Кривые параболического потенциала символизируют энергию взаимодействия между хромофорами и растворителем. Гауссовы кривые представляют распределение этой энергии взаимодействия.

Соображения Франка – Кондона также могут быть применены к электронным переходам хромофоров, растворенных в жидкостях. При таком использовании метафоры Франка – Кондона колебательные уровни хромофоров, а также взаимодействия хромофоров с фононами в жидкости продолжают вносить вклад в структуру спектров поглощения и излучения, но эти эффекты рассматриваются отдельно и независимо.

Рассмотрим хромофоры, окруженные молекулами растворителя. Эти окружающие молекулы могут взаимодействовать с хромофорами, особенно если молекулы растворителя полярны. Эта ассоциация между растворителем и растворенным веществом называется сольватацией и представляет собой стабилизирующее взаимодействие, то есть молекулы растворителя могут перемещаться и вращаться до тех пор, пока энергия взаимодействия не будет сведена к минимуму. Само взаимодействие включает электростатические и силы Ван-дер-Ваальса, а также может включать водородные связи. Принципы Франка – Кондона могут применяться, когда взаимодействия между хромофором и окружающими молекулами растворителя различны в основном и в возбужденном электронном состоянии. Это изменение взаимодействия может происходить, например, из-за различных дипольных моментов в этих двух состояниях. Если хромофор начинается в своем основном состоянии и близок к равновесию с окружающими молекулами растворителя, а затем поглощает фотон, который переводит его в возбужденное состояние, его взаимодействие с растворителем будет далеко от равновесия в возбужденном состоянии. Этот эффект аналогичен первоначальному принципу Франка – Кондона: электронный переход происходит очень быстро по сравнению с движением ядер - перестройкой молекул растворителя в случае сольватации. Теперь мы говорим о вертикальном переходе, но теперь горизонтальная координата - это пространство взаимодействия растворителя и растворенного вещества. Эта координатная ось часто обозначается как «Координата сольватации» и представляет несколько абстрактно все соответствующие измерения движения всех взаимодействующих молекул растворителя.

Согласно первоначальному принципу Франка – Кондона, после электронного перехода молекулы, оказавшиеся в более высоких колебательных состояниях, немедленно начинают релаксировать в низшие колебательные состояния. В случае сольватации молекулы растворителя немедленно попытаются перегруппироваться, чтобы минимизировать энергию взаимодействия. Скорость релаксации растворителя зависит от вязкости растворителя. Предполагая, что время релаксации растворителя мало по сравнению со временем жизни электронного возбужденного состояния, излучение будет происходить из состояния с наименьшей энергией растворителя возбужденного электронного состояния. Для низкомолекулярных растворителей, таких как вода или метанол при температуре окружающей среды, время релаксации растворителя составляет порядка нескольких десятков пикосекунд, тогда как время жизни в возбужденном состоянии хромофора составляет от нескольких пикосекунд до несколько наносекунд. Сразу после перехода в основное электронное состояние молекулы растворителя также должны перестроиться, чтобы приспособиться к новой электронной конфигурации хромофора. Рисунок 7 иллюстрирует принцип Франка – Кондона, примененный к сольватации. Когда раствор освещается светом, соответствующим энергии электронного перехода, некоторые хромофоры переходят в возбужденное состояние. Внутри этой группы хромофоров будет статистическое распределение энергий взаимодействия растворитель-хромофор, представленное на рисунке функцией распределения Гаусса. Взаимодействие растворитель-хромофор изображено как параболический потенциал в обоих электронных состояниях. Поскольку электронный переход происходит практически мгновенно во временной шкале движения растворителя (вертикальная стрелка), совокупность хромофоров в возбужденном состоянии сразу далеки от равновесия. Перестройка молекул растворителя в соответствии с новой кривой потенциальной энергии представлена изогнутыми стрелками на рисунке 7. Обратите внимание, что хотя электронные переходы квантованы, энергия взаимодействия хромофора с растворителем рассматривается как классический континуум из-за большого количества вовлеченные молекулы. Хотя излучение изображено как происходящее из минимума потенциала взаимодействия хромофор-растворитель в возбужденном состоянии, значительное излучение может иметь место до достижения равновесия, когда вязкость растворителя высока или время жизни возбужденного состояния невелико. Разница в энергии между поглощенными и испускаемыми фотонами, изображенная на рисунке 7, является вкладом сольватации в стоксов сдвиг.

См. Также

Ссылки

^Franck, J. (1926). «Элементарные процессы фотохимических реакций». Труды общества Фарадея. 21 : 536-542. doi : 10.1039 / tf9262100536.

Дополнительная литература

Franck, J. (1926). «Элементарные процессы фотохимических реакций». Труды общества Фарадея. 21 : 536–542. doi : 10.1039 / tf9262100536.Ссылка
Кондон, Э. (1926). «Теория распределения интенсивности в полосовых системах (тезисы собрания)». Physical Review. 27(5): 640. Bibcode : 1926PhRv... 27..637.. doi : 10.1103 / PhysRev.27.637.
Кондон, Э. (1926). «Теория распределения интенсивности в полосовых системах». Физический обзор. 28 (6): 1182–1201. Полномочный код : 1926PhRv... 28.1182C. doi : 10.1103 / PhysRev.28.1182.Ссылка
Кондон, Э. (1928). «Ядерные движения, связанные с электронными переходами в двухатомных молекулах». Физический обзор. 32 (6): 858–872. Bibcode : 1928PhRv... 32..858C. doi : 10.1103 / PhysRev.32.858.Ссылка
Бирдж, Р. Т. (1926). «Полосные спектры окиси углерода». Физический обзор. 28 (6): 1157–1181. Полномочный код : 1926PhRv... 28.1157B. doi : 10.1103 / PhysRev.28.1157.Ссылка
Нойес, У.А. (1933). «Соотношение спектроскопии и фотохимии». Обзоры современной физики. 5(4): 280–287. Bibcode : 1933RvMP.... 5..280N. doi : 10.1103 / RevModPhys.5.280.Ссылка
Кулидж, А.С., Джеймс, Х. М. и Настоящее, Р. Д. (1936). «Исследование принципа Франка – Кондона». Журнал химической физики. 4(3): 193–211. Bibcode : 1936JChPh... 4..193C. doi : 10.1063 / 1.1749818. CS1 maint: несколько имен: список авторов (ссылка )Ссылка
Герцберг, Герхард (1971). Спектры и структуры простых свободных радикалов. Нью-Йорк: Довер. ISBN 0-486-65821-X.
Харрис, Дэниел C.; Майкл Д. Бертолуччи (1978). Симметрия и спектроскопия. Нью-Йорк: Довер. ISBN 0-486-66144-X.
Бернат, Питер Ф. (1995). Спектры атомов и молекул (разделы физической химии). Oxford: Oxford University Press. ISBN 0-19-507598-6.
Аткинс, PW; RS Friedman (1999). Molecular Quantum Mechanics. Oxford: Oxford University Press. ISBN 0-19-855947-X.

Внешние ссылки